ویکیجزوه/دانشکده:فنی و مهندسی/انتقال حرارت/حل عددی مسائل هدایت، پایا و گذرا
روش تفاضل محدود برای هدایت دایمی
[ویرایش]گسسته سازی معادله گرما
[ویرایش]
.تقریب پیشرو:
خطا از مرتبهٔ
است.
تقریب پسرو:
خطااز مرتبهٔ
است.
در اینجا برای حل مسایل از روش حجم محدود استفاده میکنیم که معادلهٔ بقای حجم را روی سلول مینویسیم.
درحالت دایمی که تولید نیز داشته باشیم:
حل عددی برای هدایت دایمی یک بعدی با روش حجم محدود
[ویرایش]
دستگاه معادلات
برای هر نقطه یا معادله یا مقدار آن را داریم.
n معادله و n مجهول داریم.
با حل دستگاه بالا دمای کل گرهها رو بدست میآوریم.
مثالها
[ویرایش]مثال1
با استفاده از روش حجم محدود (شکل ۱) معادله گرما بصورت زیر تبدیل خواهد شد:
از بقای انرژی برای هر سلول داریم:
- قرارداد: از آنجا که جهت شار گرمایی معلوم نیست فرض را بر این میگذاریم که تمام شارهای گرمایی بصورت ورودی به سیستم باشند.
برای بدست آوردن مقدار گرمای وارد یا خارج شده از دیوار، با نوشتن بقای انرژی برای قسمت هاشور خورده خواهیم داشت:
مثال2
دمای نقاط نمایش داده شده در شکل ۲ را به روش عددی در دیوار مسطح زیر گسسته کنید.
نقطهٔ صفر:
نقطهٔ یک:
نقطهٔ دو:
نقطهٔ سه:
حل عددی در هندسههای متغییر دایمی یک بعدی با روش حجم محدود
[ویرایش]
حل عددی هدایت دایمی دو بعدی با روش حجم محدود
[ویرایش]هدف: حل عددی معادله پخش گرما در حالت دایمی
راه حل: المانی را به صورت زیر در نظر میگیریم. و معادله پخش گرما در حالت دایمی را برای ان مینویسیم. از معادله پخش گرما برای حالت دایمی روی حجم انتگرال میگیریم.
معادله پخش گرما برای حالت دایمی:
انتگرال گیری روی حجم از معادله پخش گرما:
که f همان W، E، S و N میباشد.
با فرض ثابت بودن k، معادلات را میتوان به صورت زیر نوشت.
روش دوم:
میتوانیم برای یک المان همه انتقال حرارتی را که با اطراف دارد، به صورت ورودی در نظر بگیریم و با هم جمع کنیم:
مثال3
در شکل زیر با توجه به اطلاعات داده شده:
الف: دمای نقاط را بدست آورید.
ب: شار ورود به سیستم را بدست آورید.
نقطه ۵:
{
نقطه ۶:
نقطه ۷:
نقطه ۸:
نقطه ۹:
نقطه ۱۰:
نقطه ۱۱:
بقای انرژی:
نقطه ۱۲:
بقای انرژی:
نقطه ۱۳:
نقطه ۱۴:
نقطه ۱۵:
حال با حل ماتریس زیر به روش ماتریس معکوس یا هر روشی که معتبر باشد میتوان دما در نقاط مختلف را بدست آورد:
A: ماتریس ضرایب
T: ماتریس دما
B: ماتریس معلومات
حال برای بدست آوردن شار ورودی به سیستم، المانی از پایین جسم جدا میکنیم.(از آنجا که انتقال حرارت پایا میباشد پس شار ورودی و شار خروجی یکسان میباشند.)
مثال4
در شکل نشان داده شده اگر T1=430 و T3=394 و T6=492 و ضریب رسانندگی برابر ۱w/m.k و ضریب انتقال جابجایی برابر ۵۰w/m2 .k باشد:
الف) دمای سایر نقاط را بدست آورید.
ب) میزان کل انتقال حرارت را بدست آورید.
با توجه به شکل میتوان دمای نقطهٔ ۸ و ۹ را به راحتی محاسبه کرد:
حال از روش تفاضل محدود معادلات را بدست میآوریم، یعنی برای هر نقطه تمام انتقال حرارتی را که به اطراف دارد به صورت وارد به نقطه مورد نظر، در نظر میگیریم.
پس داریم:
حال با حل دستگاه ۴ معادله ۴ مجهول از طریق حل ماتریس AX=B که
A ماتریس ضرایب
B ماتریس معلومات
X ماتریس دما
است به روش معکوس داریم:
حال برای محاسبهٔ انتقال حرارت به دلیل پایا بودن انتقال حرارت، هم میتوان انتقال حرارت از نقاط ۱و ۲و ۳و ۴ بدست آورد و هم از نقاط ۸و ۹. پس داریم:
میدانیم که دمای نقطهٔ ۸و۹ با هم برابر پس:
روش تفاضل محدود برای هدایت گذرا
[ویرایش]روش صریح
[ویرایش]گسستهسازی معادله گرما
[ویرایش]
در روش صریح تفاضل محدود دمای هر گره در زمان را از اطلاعات مربوط به دمای هر گره و گرههای مجاور در زمان قبلی t میتوان محاسبه کرد (از اندیس P برای نشان دادن وابستگی T به زمان استفاده میشود)
با حل گره در زمان جدید (P+1) و با فرض اینکه داریم:
که در آن Fo شکل تفاضل محدود عدد فوریه است.
اگر سیستم یک بعدی و در جهت x باشد شکل صریح معادله تفاضل برای گره داخلی m به صورت زیر است:
در معادلههای صریح دماهای مجهول گرهها در زمان جدید فقط توسط دماهای معلوم گرهها در زمان قبل تعیین میشوند. لذا محاسبه دماهای مجهول سر راست است.
با کاهش مقادیر و میتوان دقت حل تفاضل محدود را افزایش داد. البته با کاهش تعداد گرههایی که باید بررسی شوند افزایش و با کاهش تعداد بازههای زمانی برای نیل به زمان نهایی افزایش مییابد
یک عیب روش صریح این است که پایداری آن بی قید و شرط نیست. در مسایل گذرا با گذشت زمان دمای گرهها باید به طور پیوسته به مقادیر نهایی نزدیک تر شوند ولی با روش صریح این حل با نوسانهای عددی (که بطور فیزیکی غیر ممکن هستند) مشخص میشوند. نوسانها ممکن است ناپایدار باشند و در نتیجه جوابها از شرایط پایای واقعی دور شوند. برای جلوگیری از این نتایج گول زننده را باید از یک حد مشخص کمتر در نظر گرفت. این وابستگی زمان را معیار پایداری گویند.
معیار پایداری ایجاب میکند که ضریب مربوط به گره مورد نظر در زمان قبل بزرگ تر یا مساوی با صفر باشد.
در نتیجه برای یک گره داخلی یک بعدی Fo باید کوچکتر یا مساوی باشد
و برای یک گره داخلی دو بعدی Fo باید کوچکتر یا مساوی باشد.
مطابق شکل بالا یک دیوار با انتقال حرارت یک بعدی گذرا مفروض می باشد و مقادیر دمای نقطه صفر و ضریب جابه جایی معلوم میباشد بنا به حل عددی صریح میتوان مسئله را به صورت زیر برای نقاظ نشان داده شده حل نمود:
گره صفر:
گره ۱:
گره ۲:
گره ۳:
همانطور که قبلا ذکر شد روش حل صریح پایداری مشروط دارد و گام زمانی آن را مشابه زیر برای تمامی نقاط میتوان بدست آورد. کمترین بازه زمانی شرط پایداری میباشد.
مثالها
[ویرایش]مثال 5
نمای بالای دودکشی را ملاحظه میکنید که میتواند مصداقی از انتقال حرارت دو بعدی گذرا باشد و دمای گازهای خارج شده از دودکش و محیط و خواص در ادامه آمده است با فرض مقدار ضریب جابه جایی مطابق زیر حداقل گام زمانی برای پایداری را بدست آورید.
حل: با توجه به متقارن بودن دهانه خروجی دودکش میتوان مسئله را برای حل نمود و تعمیم داد:
گره ۱:
گره ۲:
گره ۳ همانند گره ۲
گره ۴:
گره ۵:
گره ۶:
گره ۷:
گره ۱:
گره ۲ و۳:
گره ۴:
گروه ۵ و ۶ و ۷:
روش ضمنی
[ویرایش]گسسته سازی معادله گرما
[ویرایش]
در روش صریح تفاضل محدود دمای هر گره در زمان را از اطلاعات مربوط به دمای هر گره وگرههای مجاور در زمان قبلی میتوان محاسبه کرد. لذا تعیین دمای یک گره در هر لحظه مستقل از دمای سایر گرهها در همان لحظه است، گر چه محاسبه با این روش ساده است ولی محدودیتهایی برای انتخاب وجود دارد.
برای یک نمو مکانی معین بازه زمانی باید با شرایط پایداری سازگار باشد. در نتیجه اغلب باید از مقادیر بسیار کوچک استفاده شود و برای رسیدن به حل مسئله تعداد بسیار زیادی بازه زمانی لازم میشود. اغلب با استفاده از روش ضمنی تفاضل محدود به جای روش صریح میتوان زمان محاسبه را کاهش داد.
با ارزیابی سایر دماها در زمان جدید به جای زمان قبلی میتوان شکل ضمنی معادله تفاضل محدود را بدست آورد.
شکل ضمنی برای یک گره داخلی یک سیستم دو بعدی عبارت است از:
با مرتب کردن و به فرض نتیجه میشود:
از معادله فوق واضح است که دمای جدید به دماهای جدید گرههای مجاورش که معمولا مجهولند بستگی دارد. لذا برای تعیین دماهای مجهول گرهها در معادلههای گرهای متناظر را باید همزمان حل کرد.
این حل با استفاده از روش گوس-سیدل یا با معکوس سازی ماتریس انجام میشود. لذا حل پیش رو شامل حل همزمان معادلههای گرهای در لحظات است که تا نیل به زمان نهایی دلخواه ادامه یابد.
فرمول بندی ضمنی نسبت به روش صریح این مزیت مهم را دارد که بدون قید و شرط همواره برای تمام بازههای مکانی و زمانی پایدار است. و هیچ قیدی برای و وجود ندارد.
چون در روش ضمنی میتوان از مقادیر بزرگتر استفاده کرد زمان محاسبه کاهش یافته و دقت نیز کمی کاهش مییابد.
با وجود این برای دستیابی به دقت زیاد باید به اندازه کافی کوچک باشد تا نتایج از کاهش بیشتر مستقل شوند.
شکل ضمنی را با روش موازنه انرزی نیز میتوان بدست آورد. به عنوان مثال برای جابجایی و رسانش گذرای یک بعدی به صورت زیر است.

برای گره سطحی
برای هر گره داخلی
انتقال حرارت یک بعدی
توضیحات داده شده در بالا را میتوان مطابق شکل زیر برای دیواری یک بعدی با انتقال حرارت گذرا که با گرههای ۰و۱و۲و۳ نشان داده شده است مطابقت داد.
گره ۱:
گره ۲:
گره ۳:
انتقال حرارت دو بعدی

مثال6
یک فین الومینیومی باk=180 و سطح مقطع مثلثی که طول آن L=5 cm و مقطع آن b=1 cm و عرض خیلی زیاد را در نظر بگیرید. مبنای فین با دمای درجهٔ سانتیگراد است. فین دمای خود را در معرض دمای محیط ۲۵ درجهٔ سانتیگراد با از دست میدهد با استفاده از روش تفاضل محدود دمای تمام نقاط را بیابید.













![{\displaystyle {\begin{aligned}&\sum {q}=-kA{\frac {T-{{T}_{0}}}{\Delta x}}-kA{\frac {{{T}_{1}}-{{T}_{2}}}{\Delta x}}=kA{\frac {{{T}_{0}}-2{{T}_{1}}+{{T}_{2}}}{\Delta x}}\\&{{q}_{gen}}=q_{gen}^{'''}\Delta xA\\&\\&k{\frac {{{T}_{0}}-2{{T}_{1}}+{{T}_{2}}}{\Delta {{x}^{2}}}}+q_{ge{{n}_{1}}}^{'''}=0\\&k{\frac {{{T}_{1}}-2{{T}_{2}}+{{T}_{3}}}{\Delta {{x}^{2}}}}+q_{ge{{n}_{2}}}^{'''}=0\\&k{\frac {{{T}_{2}}-2{{T}_{3}}+{{T}_{4}}}{\Delta {{x}^{2}}}}+q_{ge{{n}_{3}}}^{'''}=0\\&{{T}_{0}}={{T}_{0}}\\&{{T}_{4}}={{T}_{l}}\\&-2{{T}_{1}}+{{T}_{2}}=-q_{gen}^{'''}{\frac {\Delta {{x}^{2}}}{k}}-{{T}_{0}}\\&{{T}_{1}}-2{{T}_{2}}+{{T}_{3}}=-q_{gen}^{'''}{\frac {\Delta {{x}^{2}}}{k}}\\&{{T}_{2}}-2{{T}_{3}}=-q_{gen}^{'''}{\frac {\Delta {{x}^{2}}}{k}}-{{T}_{l}}\\&AT=B\\&A=\left[{\begin{matrix}-2&1&0\\1&-2&1\\0&1&-2\\\end{matrix}}\right]\\&T=\left[{\begin{aligned}&{{T}_{1}}\\&{{T}_{2}}\\&{{T}_{3}}\\\end{aligned}}\right]\\&B=-{\frac {\Delta {{x}^{2}}}{k}}\left[{\begin{aligned}&q_{ge{{n}_{1}}}^{'''}\\&q_{ge{{n}_{2}}}^{'''}\\&q_{ge{{n}_{3}}}^{'''}\\\end{aligned}}\right]+\left[{\begin{aligned}&{{T}_{0}}\\&0\\&{{T}_{l}}\\\end{aligned}}\right]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed27c13b0d3fb22171c0ca20c29c11bbc077d293)
![{\displaystyle {\begin{aligned}&q+kA{\frac {{{T}_{1}}-{{T}_{0}}}{\Delta x}}+q_{ge{{n}_{0}}}^{'''}{\frac {\Delta x}{2}}A=0\\&q=-A[k{\frac {{{T}_{1}}-{{T}_{0}}}{\Delta x}}+q_{ge{{n}_{0}}}^{'''}{\frac {\Delta x}{2}}]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9795ee8c683d250ff118f9e245384e621a2cace4)




![{\displaystyle {\begin{aligned}&0=kA{\frac {{{T}_{2}}-{{T}_{3}}}{\Delta x}}+\alpha {{q}_{s}}-\left[\varepsilon \sigma ({{T}_{surr}}^{4}-{{T}_{3}}^{4})={{h}_{r}}A({{T}_{surr}}-{{T}_{3}})\right]\\&{{h}_{r}}=\varepsilon \sigma ({{T}_{surr}}^{2}+{{T}_{3}}^{2})({{T}_{surr}}+{{T}_{3}})\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efd182a31f89fd253889abf1857037e6dec68182)
![{\displaystyle {\begin{aligned}&{{T}_{2}}-(1-{\frac {{{h}_{r}}\Delta x}{k}}){{T}_{3}}=-{\frac {{{h}_{r}}\Delta x}{k}}-\alpha {{q}_{s}}^{'''}\\&\left[{\begin{matrix}-2&1&0\\1&-2&1\\0&1&-(1-{\frac {{{h}_{r}}\Delta x}{k}})\\\end{matrix}}\right]\left[{\begin{aligned}&{{T}_{1}}\\&{{T}_{2}}\\&{{T}_{3}}\\\end{aligned}}\right]=\left[{\begin{aligned}&-{{T}_{0}}\\&0\\&{\frac {{{h}_{r}}\Delta x}{k}}{{T}_{surr}}-\alpha {{q}_{s}}^{'''}\\\end{aligned}}\right]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/85cae0518eee5aa8cce6ca806b60e13bd6439775)



![{\displaystyle \int \limits _{c.v.}{[{\overrightarrow {\nabla }}.(k{\overrightarrow {\nabla }}T)+q_{gen}^{'''}]dV=0\to \int \limits _{c.s.}{k{\overrightarrow {\nabla }}T.d{\overrightarrow {s}}+\int \limits _{V}{q_{gen}^{'''}dV=0}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95feb9138740b23b606d0ea24d0c365c0c57e844)




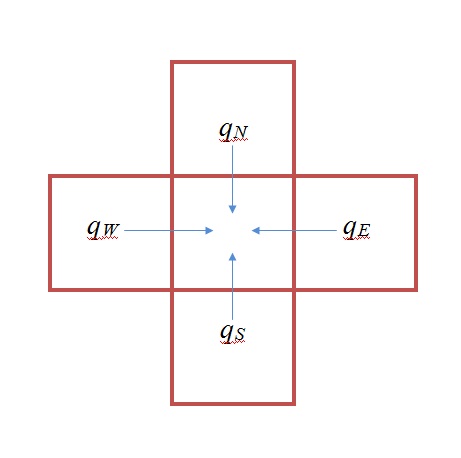
![{\displaystyle {\begin{aligned}&{{q}_{e}}+{{q}_{w}}+{{q}_{n}}+{{q}_{s}}+q_{gen,i,j}^{'''}\Delta x\Delta yb=0\\&{{q}_{e}}=k\Delta yb{\frac {{{T}_{i+1,j}}-{{T}_{i,j}}}{\Delta x}}\\&{{q}_{w}}=k\Delta yb{\frac {{{T}_{i-1,j}}-{{T}_{i,j}}}{\Delta x}}\\&{{q}_{n}}=k\Delta xb{\frac {{{T}_{m,n+1}}-{{T}_{m,n}}}{\Delta y}}\\&{{q}_{s}}=k\Delta xb{\frac {{{T}_{m,n-1}}-{{T}_{m,n}}}{\Delta y}}\\&\Rightarrow k\Delta x\Delta y\left[{\frac {{{T}_{m+1,n}}-2{{T}_{m,n}}+{{T}_{m-1,n}}}{\Delta {{x}^{2}}}}+{\frac {{{T}_{m,n-1}}-2{{T}_{m,n}}+{{T}_{m,n+1}}}{\Delta {{y}^{2}}}}\right]+q_{ge{{n}_{m,n}}}^{'''}\Delta x\Delta yb=0\\&k({\frac {{{\partial }^{2}}T}{{{\partial }^{2}}x}}+{\frac {{{\partial }^{2}}T}{{{\partial }^{2}}y}})+q_{gen}^{'''}=0\\&if:\Delta x=\Delta y\to k[{{T}_{m+1,n}}+{{T}_{m-1,n}}+{{T}_{m,n-1}}+{{T}_{m,n+1}}+-4{{T}_{m,n}}]+q_{gen}^{'''}\Delta {{x}^{2}}=0\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4462d7e209351e65cdf3abdc46dc5143d81a4a3)



![{\displaystyle {\begin{aligned}&{{q}_{w}}=0\\&{{q}_{e}}=k\Delta yb{\frac {{{T}_{6}}-{{T}_{5}}}{\Delta x}}\\&{{q}_{n}}=k\Delta xb{\frac {{{T}_{9}}-{{T}_{5}}}{\Delta y}}\\&{{q}_{s}}=k\Delta xb{\frac {{{T}_{1}}-{{T}_{5}}}{\Delta y}}\\&\Delta x=\Delta y\\&{{q}_{w}}+{{q}_{e}}+{{q}_{n}}+{{q}_{s}}=0\\&kb[0+2{{T}_{6}}-{{T}_{1}}+{{T}_{9}}-4{{T}_{5}}]=0\\&\to {{T}_{6}}+{{T}_{9}}-4{{T}_{5}}={{T}_{0}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3107458744bffb871a4e3230c9987ee10ef906d0)














































































![{\displaystyle 2kw[L-(m-{\frac {1}{2}})\Delta x]\tan \theta {\frac {{{T}_{m-1}}-{{T}_{m}}}{\Delta x}}+2kw[L-(m+{\frac {1}{2}})\Delta x]\tan \theta {\frac {{{T}_{m-1}}-{{T}_{m}}}{\Delta x}}+h{\frac {2w\Delta x}{\cos \theta }}({{T}_{\infty }}-{{T}_{m}})=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b8fc8b9e56474134435a80f627fcda48b616822)
+[1-(m+{\frac {1}{2}}){\frac {\Delta x}{L}}]({{T}_{m-1}}-{{T}_{m}})+h{\frac {\Delta {{x}^{2}}}{kl\sin \theta }}({{T}_{\infty }}-{{T}_{m}})=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0650c5050134fa608c080d656c54f5c4cdfdfc06)


