افت هد لوله مساوی با تغییر مجموع فشار و نیروی ثقل است که در واقع تغییر ارتفاع تراز هیدرولیکی(HGL) است
در مکانیک سیالات ۱ دو نوع اتلاف انرژی برای لوله ها در نظر می گیریم: یکی از انها افت بر اثر تغییر قطر لوله ها و انواع اتصالات (Minor Loss) و دیگری افت بر اثر اصطکاک در لوله ها (Major loss) که مقدار آن نسبت به دیگری بیشتر است.
در این مبحث افت بر اثر تغییر قطر لوله ها و اتصالات را بررسی می کنیم و در خلال این بررسی سعی می کنیم تا حد زیادی با انواع شیرها و هدر رفتن انرژی در آنها آشنا شویم، در پایان نیز به بررسی انواع مسائل خط لوله می پردازیم.
ابتدا در مورد افت بر اثر تغییر قطر لوله و وجود انواع اتصالات بحث می کنیم و پس از آن توضیحاتی راجع به افت بر اثراصطکاک می دهیم.
عواملی چون تغییر قطر لوله ها و وجود انواع اتصالات (مانند زانو، انواع شیرها، وجود انحنا در لوله ها و ...) باعث تغییر شکل خطوط جریان و ایجاد گردابه ها (vortex) و در نتیجه هدر رفتن انرژی می شود. این نوع اتلاف با فرمول زیر قابل محاسبه می باشد:
k : ضریب اتلاف انرژی موضعی (ضریبی تجربی که از جداول مربوطه به دست می آید و بدون بعد است.)
v : سرعت جریان (معمولا سرعت ورودی را در نظر می گیریم)
K : نمادی از تلفات انرژی محسوب می شود، مثلا هنگامی که قطر لوله به صورت ناگهانی افزایش یابد به گونهای که نسبت A1 /A2 تقریبا برابر صفر شود (A1 <<A2 ) آنگاه k را برابر یک در نظر می گیریم و این بدان معناست که کل انرژی جریان تلف شده است. (به انرزی حرارتی تبدیل شده است.)
برای یافتن k مقاطع مختلف می توان به جداول موجود در کتابهای مرجع درس مکانیک سیالات مراجعه کرد اما در ادامه سعی می کنیم به همین بهانه به انواع شیرهای موجود و ضریب اتلاف انرژی موضعی آنها بپردازیم.
شیرهایی که در اینجا بررسی می کنیم عبارتند از:
در سیستم لوله ای علاوه بر افت اصطکاکی از نوع مودی ،که برای طول لوله محاسبه می شود،افتهای دیگری تحت عنوان افتهای موضعی به دلایل زیر وجود دارد:
1.ورودی یا خروجی لوله:
سیال قبل از ورود یا خروج از لوله دارای سطح و فشار متفاوتی نسبت به ورودی و خروجی لوله بوده است و هنگام ورود یا از خروج از لوله باید دبی جریان تغییر کند پس افت جزیی را خواهیم داشت.در حقیقت ورودی یا خروجی لوله مانند مانعی دربرابر عبور جریان(دبی)خواهند بود
2.بزرگ یا کوچک شدن ناگهانی مقطع:
بزرگ یا کوچک شدن ناگهانی مقطع باعث افت یا افزایش سیال خواهد شد که خود افت جزئی یا خطایی را در بر خواهد داشت.مانند عبور از سیال از نازل یا برعکس آن که باعث افت یا افزایش فشار خواهد شد و تغییر ایجاد می کند.
3.اتصالات به کار رفته در سیستم ،مانند زانویی ،سه راهی و ... :
اتصالات در حقیقت و در واقع مانند مانعی ناگهانی دربرابر جریان عمل می کنند و مقداری از انرژی سیال را می گیرند که خود باعث خطا می شود
4.شیرها ،در حالت باز و نیمه باز:
شیرها هم مانند اتصالات ایجاد مانع می کنند و باعث تغییر در روند حرکت سیال خواهند شد و هرچقدر شیر بسته تر باشد فشار بیشتر افت می کند و قدرت بیشتری از بین خواهد رفت وخطا بیشتر خواهد بود.مثال بارز آن شیر فشار شکن است
5.اثر تغییر قطر لوله بر حداکثر فشار ایجاد شده در اثر بسته شدن یک شیر در زمان مشخص:
با افزایش قطر لوله ، هد سیستم کاهش می یابد و این روند کاهش به تدریج با افزایش قطر کم می شود یعنی در دبی ثابت حساسیت هد سیستم نسبت به قطر لوله با افزایش قطر لوله کم می شود.
6.تغییرات هد ماکزیمم ناشی از بسته شدن سریع شیر در مقابل تغییرات ضخامت لوله:
اگر لوله جدار نازک نباشد : در یک دبی ثابت حداکثر فشار ناشی از بسته شدن سریع یک شیر با افزایش ضخامت لوله ، افزایش می یابد.
اگر لوله جدار نازک باشد :در یک دبی ثابت حداکثر فشار ناشی از بسته شدن سریع یک شیر با افزایش ضخامت لوله ، همانند حالت اول افزایش می یابد.
7.بزرگ یا کوچک شدن تدریجی مقطع:
این عامل هم باعث افت تدریجی در لوله خواهد شد که در نهایت می تواند با کاهش مقطع فشار را کاهش و سرعت را افزایش دهد(نازل) و یا برعکس(دیفیوزر)
این افتها ممکن است چندان هم کوچک نباشند ،مانند افت حاصل از یک شیر نیمه باز که میتواند حتی بیش از یک لوله ی طویل افت فشار ایجاد کند .از آنجا که الگوی جریان در اتصلات و شیر ها خیلی پیچیده است در مورد آنها نمی توان یک تئوری قوی ارائه کرد.افتهای مربوط به آنها را معمولا با آزمایش اندازه گیری کرده و با پارامترهای جریان ارتباط می دهند.داده ها،مخصوصا برای شیرها،به نحوه طراحی سازنده آن بستگی دارد.بنابراین مقادیر به صورت تخمینی در نظر گرفته می شوند. افت موضعی اندازه گیری شده معمولا به صورت نسبی از هد تلف شده ی وسیله مورد نظر،به سرعت سیستم لوله بیان می شود.
h
m
=
k
(
v
2
2
g
)
{\displaystyle {{h}_{m}}=k({\frac {{v}^{2}}{2g}})}
در مبحث افت اصطکاکی در اتصالات می توان مقدار ان را معادل مقداری از افت اصطکاکی موجود در لوله قرار داد و لازم است که طول معادل را بدست اورد:
{
h
f
1
=
f
L
1
D
1
V
1
2
2
g
h
m
=
k
V
1
2
2
g
=
f
L
e
q
D
1
V
1
2
2
g
}
→
L
e
q
=
k
D
1
f
{\displaystyle \left\{{\begin{aligned}&{{h}_{{f}_{1}}}=f{\frac {{L}_{1}}{{D}_{1}}}{\frac {{{V}_{1}}^{2}}{2g}}\\&{{h}_{m}}=k{\frac {{{V}_{1}}^{2}}{2g}}=f{\frac {{L}_{eq}}{{D}_{1}}}{\frac {{{V}_{1}}^{2}}{2g}}\\\end{aligned}}\right\}\to {{L}_{eq}}={\frac {k{{D}_{1}}}{f}}}
گفتنی است که تمام داده های ضریب بی بعد K تقریبا برای شرایط متلاطم است.
اتلاف کل برای یک سیستم لوله کشی، با قطر ثابت، چنین است:
Δ
h
t
o
t
=
h
f
+
∑
h
m
=
v
2
2
g
(
f
L
D
+
∑
K
)
{\displaystyle \Delta {{h}_{tot}}={{h}_{f}}+\sum \limits _{}^{}{{h}_{m}}={\frac {{v}^{2}}{2g}}\left({\frac {fL}{D}}+\sum \limits _{}^{}{K}\right)}
..............................................................................................................................
افت های جزئی: زانویی در سمت چپ و سه راهی در سمت راست.
..............................................................................................................................
انبساط ناگهانی:
بدست آوردن K وقتی سیال از لوله ای با سطح مقطع
A
1
{\displaystyle {{A}_{1}}}
A
2
{\displaystyle {{A}_{2}}}
P
m
=
P
1
→
c
o
n
s
e
r
v
a
t
i
o
n
o
f
m
a
s
s
m
˙
i
n
=
m
˙
o
u
t
→
ρ
v
1
A
1
=
ρ
v
2
A
2
(
m
˙
v
)
i
n
−
(
m
˙
v
)
o
u
t
+
∑
f
x
=
0
→
ρ
A
1
V
1
2
−
ρ
A
2
V
2
2
+
P
m
A
2
−
P
2
A
2
=
0
→
P
1
−
P
2
=
P
m
−
p
2
=
ρ
(
A
1
A
2
V
1
2
−
V
2
2
)
=
ρ
A
1
A
2
V
1
2
(
1
−
A
1
A
2
)
(
P
ρ
g
+
v
2
2
g
+
z
)
1
−
(
P
ρ
g
+
v
2
2
g
+
z
)
2
=
h
m
→
h
m
=
P
1
−
P
2
2
g
+
v
1
2
−
v
2
2
2
g
=
v
1
2
g
×
A
1
A
2
(
1
−
A
1
A
2
)
+
v
1
2
2
g
(
1
−
(
A
1
A
2
)
2
)
=
v
1
2
2
g
(
1
−
A
1
A
2
)
2
K
=
(
1
−
A
1
A
2
)
2
{\displaystyle {\begin{aligned}&{{P}_{m}}={{P}_{1}}\\&{\xrightarrow {conservation~~of~~mass}}{{\dot {m}}_{in}}={{\dot {m}}_{out}}\to \rho {{v}_{1}}{{A}_{1}}=\rho {{v}_{2}}{{A}_{2}}\\&{{\left({\dot {m}}v\right)}_{in}}-{{\left({\dot {m}}v\right)}_{out}}+\sum {{{f}_{x}}=0\to \rho {{A}_{1}}{{V}_{1}}^{2}-\rho {{A}_{2}}}{{V}_{2}}^{2}+{{P}_{m}}{{A}_{2}}-{{P}_{2}}{{A}_{2}}=0\\&\to {{P}_{1}}-{{P}_{2}}={{P}_{m}}-{{p}_{2}}=\rho \left({\frac {{A}_{1}}{{A}_{2}}}{{V}_{1}}^{2}-{{V}_{2}}^{2}\right)=\rho {\frac {{A}_{_{1}}}{{A}_{2}}}{{V}_{1}}^{2}\left(1-{\frac {{A}_{1}}{{A}_{2}}}\right)\\&{{\left({\frac {P}{\rho g}}+{\frac {{v}^{2}}{2g}}+z\right)}_{1}}-{{\left({\frac {P}{\rho g}}+{\frac {{v}^{2}}{2g}}+z\right)}_{2}}={{h}_{m}}\\&\\&\to {{h}_{m}}={\frac {{{P}_{1}}-{{P}_{2}}}{2g}}+{\frac {{{v}_{1}}^{2}-{{v}_{2}}^{2}}{2g}}={\frac {{{v}_{1}}^{2}}{g}}\times {\frac {{A}_{1}}{{A}_{2}}}\left(1-{\frac {{A}_{1}}{{A}_{2}}}\right)+{\frac {{{v}_{1}}^{2}}{2g}}\left(1-{{\left({\frac {{A}_{1}}{{A}_{2}}}\right)}^{2}}\right)={\frac {{{v}_{1}}^{2}}{2g}}{{\left(1-{\frac {{A}_{1}}{{A}_{2}}}\right)}^{2}}\\&K={{\left(1-{\frac {{A}_{1}}{{A}_{2}}}\right)}^{2}}\\\end{aligned}}}
در محاسبه
h
m
{\displaystyle {{h}_{m}}}
سرعت قبل از اتصال ضرب می کنیم.
(
P
ρ
g
+
v
2
2
g
+
z
)
1
−
(
P
ρ
g
+
v
2
2
g
+
z
)
2
=
∑
i
f
i
+
∑
j
h
m
,
j
=
∑
i
(
f
i
l
i
D
i
×
v
i
2
2
g
)
+
∑
j
k
j
v
i
2
2
g
{\displaystyle {{\left({\frac {P}{\rho g}}+{\frac {{v}^{2}}{2g}}+z\right)}_{1}}-{{\left({\frac {P}{\rho g}}+{\frac {{v}^{2}}{2g}}+z\right)}_{2}}=\sum \limits _{i}{{f}_{i}}+\sum \limits _{j}{{h}_{m,j}}=\sum \limits _{i}{\left({{f}_{i}}{\frac {{l}_{i}}{{D}_{i}}}\times {\frac {{{v}_{i}}^{2}}{2g}}\right)}+\sum \limits _{j}{{{k}_{j}}{\frac {{{v}_{i}}^{2}}{2g}}}}
این پدیده در اثر اصطکاک بین سیال و لوله ها اتفاق می افتد که منجر به افت فشار سیال می شود. برای محاسبه کاهش انرژی به علت وجود اصطکاک بین لایه های سیال و ذرات سیال با جداره از فرمول زیر استفاده می شود:
ّf پارامتر بدون بعد است وآن را ضریب اصطکاک دارسی می نامند.
Δ
H
=
f
l
d
v
2
2
g
{\displaystyle \Delta \mathrm {H} =f{\frac {l}{d}}{\frac {{v}^{2}}{2g}}}
که در آن
f
{\displaystyle f}
l
{\displaystyle l}
d
{\displaystyle d}
f
{\displaystyle f}
روشی برای بررسي ميزان افت هد ناشي از اصطكاك در نشتي گاز و تاثير پارامتر هاي تاثيرگذار بر آن به روش( غير مخرب آكوستيك اميشن)
نشتي يكي از عيوب در خطوط انتقال و نگهداري نفت و گاز مي باشد. سيال عبوري از ديواره نشت دچار افت فشار شده كه بررسي ميزان افت فشار هد و تاثير آن بر ديواره نشت حائز اهميت است. يكي از روش ها براي نشت يابي و مطالعه نشتي، روش غير مخرب نشر فراصوتي (آكوستيك اميشن) مي باشد. سيال عبوري از ديواره نشت به ديواره ها تنش وارد كرده و كرنش متعاقب آن باعث ايجاد موج الاستيك در لوله يا مخزن حاوي نشت مي شود.
ّّ
تا اینجا دو عامل کاهش افت معرفی شد اما واقعیت این است که دو عامل دیگر هم در کاهش انرژی یا افت هد در سیستم های لوله کشی انتقال سیالات و پمپ ها موثرند :
[ ویرایش ] این تلفات انرژی در اثر نشتی های داخلی بوجود می آید، به این معنا که پس از اینکه فشار سیال بالا رفت بایستی از نشت آن به قسمت کم فشار جلوگیری کرد که در عمل بسته به نوع پمپ این کار به وسیله پیستون رینگ در پمپ های رفت و برگشتی و
w
e
a
r
i
n
g
{\displaystyle wearing}
شامل اصطکاک یاتاقانها و آب بندها است که با انتخاب صحیح و استفاده اصولی از روغن و سیستم روغن کاری مناسب تا حد امکان کاهش می یابد.
در شکل زیر اگر
Q
=
.233
f
t
3
.
s
−
1
,
S
G
=
.86
,
μ
=
2
×
10
−
4
l
b
f
.
s
.
f
t
−
2
,
ρ
w
=
62.4
l
b
m
.
f
t
−
3
{\displaystyle Q=.233f{{t}^{3}}.{{s}^{-1}},SG=.86,\mu =2\times {{10}^{-4}}lbf.s.f{{t}^{-2}},{{\rho }_{w}}=62.4lbm.f{{t}^{-3}}}
(
P
ρ
g
+
v
2
2
g
+
z
)
1
=
(
P
ρ
g
+
v
2
2
g
+
z
)
2
+
∑
h
f
+
∑
h
m
−
∑
h
p
(
z
2
−
z
1
)
+
f
.
L
D
.
v
2
2
g
+
(
k
i
+
k
b
+
k
v
)
.
v
2
2
g
=
h
p
{\displaystyle {\begin{aligned}&{{({\frac {P}{\rho g}}+{\frac {{v}^{2}}{2g}}+z)}_{1}}={{({\frac {P}{\rho g}}+{\frac {{v}^{2}}{2g}}+z)}_{2}}+\sum {{{h}_{f}}+}\sum {{{h}_{m}}-}\sum {{h}_{p}}\\&({{z}_{2}}-{{z}_{1}})+f.{\frac {L}{D}}.{\frac {{v}^{2}}{2g}}+({{k}_{i}}+{{k}_{b}}+{{k}_{v}}).{\frac {{v}^{2}}{2g}}={{h}_{p}}\\\end{aligned}}}
vرا بر اساس Q بدست می اوریم
و بوسیله ان Re را بدست می اوریم .
v
=
Q
A
=
.233
π
4
(
2
12
)
2
=
10.23
f
t
.
s
−
1
Re
=
ρ
v
D
μ
=
(
0.86
×
62.4
32.2
)
(
10.23
)
(
2
12
)
2
×
10
−
4
=
1.42
×
10
4
{\displaystyle {\begin{aligned}&v={\frac {Q}{A}}={\frac {.233}{{\frac {\pi }{4}}{{({\frac {2}{12}})}^{2}}}}=10.23ft.{{s}^{-1}}\\&\operatorname {Re} ={\frac {\rho vD}{\mu }}={\frac {(0.86\times {\frac {62.4}{32.2}})(10.23)({\frac {2}{12}})}{2\times {{10}^{-4}}}}=1.42\times {{10}^{4}}\\\end{aligned}}}
ε
D
{\displaystyle {\frac {\varepsilon }{D}}}
ε
D
=
0.002
2
=
10
−
3
→
f
=
0.081
{\displaystyle {\frac {\varepsilon }{D}}={\frac {0.002}{2}}={{10}^{-3}}{\xrightarrow {}}f=0.081}
حال بوسیله معادله انرژی
h
p
{\displaystyle {{h}_{p}}}
h
p
=
10
+
(
0.081.
40
2
12
+
0.5
+
0.9
+
5
)
(
10.23
2
2
(
32.2
)
)
=
34.1
f
t
{\displaystyle {{h}_{p}}=10+(0.081.{\frac {40}{\tfrac {2}{12}}}+0.5+0.9+5)({\frac {{10.23}^{2}}{2(32.2)}})=34.1ft}
w
⋅
=
h
p
γ
Q
=
(
34.1
)
(
0.86
)
(
62.4
)
(
32.2
)
(
.233
)
=
510
f
t
.
l
b
.
s
−
1
=
.99
h
p
{\displaystyle {\overset {\centerdot }{\mathop {w} }}\,={{h}_{p}}\gamma Q=(34.1)(0.86)(62.4)(32.2)(.233)=510ft.lb.{{s}^{-1}}=.99hp}
آب ، در شرایط ρ=1.94 slug/ft3 ، v = 0.00001 ft2/s ، Q = 0.2 ft3/s و از طریق یک لوله به قطر 2 اینچ و طول 400 فوت ، همراه با چندین افت موضعی ، بین دو مخزن پمپ می شود. اگر نسبت زبری 01/0 باشد ، توان لازم برای پمپ را (hp) محاسبه کنید.
حل:
معادله انرژی را بین مقاطع 1 و 2 یعنی سطوح آزاد دو مخزن را بنویسید.
(
p
ρ
g
+
V
2
2
g
+
z
)
1
=
(
p
ρ
g
+
V
2
2
g
+
z
)
2
+
h
f
−
h
p
+
∑
h
m
{\displaystyle ({\frac {p}{\rho \,g}}+{\frac {V^{2}}{2g}}+z)_{1}=({\frac {p}{\rho \,g}}+{\frac {V^{2}}{2g}}+z)_{2}+h_{f}-h_{p}+\sum h_{m}}
که در آن
h
p
{\displaystyle h_{p}}
(
P
1
)
=
(
P
2
)
{\displaystyle (P_{1})=(P_{2})}
(
V
1
)
=
(
V
2
)
{\displaystyle (V_{1})=(V_{2})}
V
1
=
0
{\displaystyle V_{1}=0}
h
p
=
z
2
−
z
1
+
h
f
+
∑
h
m
=
120
f
t
−
20
f
t
+
V
2
2
g
(
f
L
d
+
∑
K
)
{\displaystyle h_{p}=z_{2}-z_{1}+h_{f}+\sum h_{m}=120ft-20ft+{\frac {V^{2}}{2g}}({\frac {fL}{d}}+\sum K)}
اکنون با دانستن دبی جریان خواهیم داشت:
V
=
Q
A
=
0.2
f
t
3
/
s
π
(
2
12
f
t
)
2
4
{\displaystyle V={\frac {Q}{A}}={\frac {0.2ft^{3}/s}{\frac {\pi \;({\frac {2}{12}}ft)^{2}}{4}}}}
برای
ϵ
d
{\displaystyle {\frac {\epsilon \;}{d}}}
h
p
=
100
f
t
+
(
9.17
f
t
s
)
2
2
(
32.2
f
t
s
2
)
(
0.0216
(
400
)
2
12
+
12.2
)
=
100
f
t
+
84
f
t
=
184
f
t
{\displaystyle h_{p}=100ft+{\frac {(9.17{\frac {ft}{s}})^{2}}{2(32.2{\frac {ft}{s^{2}}})}}({\frac {0.0216(400)}{\frac {2}{12}}}+12.2)=100ft+84ft=184ft}
پمپ باید به آب قدرت بدهد:
P
=
ρ
g
Q
h
p
=
(
1.94
(
32.2
)
l
b
f
f
t
3
)
(
0.2
f
t
3
s
)
(
184
f
t
)
=
2300
(
f
t
.
l
b
f
)
s
{\displaystyle P=\rho \,gQh_{p}=(1.94(32.2){\frac {lbf}{ft^{3}}})(0.2{\frac {ft^{3}}{s}})(184ft)=2300{\frac {(ft.lbf)}{s}}}
ضریب تبدیل برابر است با
1
h
p
=
550
(
f
t
.
l
b
f
)
s
{\displaystyle 1h_{p}=550{\frac {(ft.lbf)}{s}}}
P
=
2300
550
=
4.2
h
p
{\displaystyle P={\frac {2300}{550}}=4.2hp}
اگر بازده پمپ حدود 70 تا 80% باشد ، توان آن حدود 6 اسب بخار خواهد بود.
مسئله های این بخش به سه دسته تقسیم میشود:
L و ε و V و Q معلوم باشند ←←←
Δ
P
=
?
,
h
f
=
?
{\displaystyle \Delta P=?~~~~~~~~~~,~~~~~~~~~~{{h}_{f}}=?}
V
,
D
→
Re
D
→
ε
D
f
→
Δ
P
,
h
f
{\displaystyle V~~,~~~~~D\to ~~~{{\operatorname {Re} }_{D}}~~~{\xrightarrow {\frac {\varepsilon }{D}}}f\to ~~~~\Delta P~~~~,~~~~{{h}_{f}}}
روش سعی و خطا
L و ε و D و Vو Q معلوم باشند←←← Vو Q مجهول هستند
f
→
f
r
o
m
e
n
e
r
g
y
e
q
u
a
t
i
o
a
n
d
f
,
Δ
P
v
→
Re
D
→
ε
D
f
{\displaystyle f{\xrightarrow {from~~energy~~equatio~~and~~f,\Delta P}}v\to {{\operatorname {Re} }_{D}}{\xrightarrow {\frac {\varepsilon }{D}}}f}
طراحی به روش سعی و خطا
h
f
,
Δ
P
,
ε
,
L
,
Q
{\displaystyle {{h}_{f}}~~,~~~\Delta P~~~,~~~\varepsilon ~~~,~~L~~~,Q}
D
→
Q
o
r
v
Re
D
→
f
→
Δ
p
o
r
h
f
D
{\displaystyle D~~~{\xrightarrow {Q~~~or~~v}}{{\operatorname {Re} }_{D}}~~~\to ~~f{\xrightarrow {\Delta p~~or~~{{h}_{f}}}}D}
همواره در استفاده از نمودار
f
−
Re
D
{\displaystyle f-{{\operatorname {Re} }_{D}}}
Re
D
⇒
f
{\displaystyle {{\operatorname {Re} }_{D}}\Rightarrow f}
استفاده از این فرمول به صورت عکس (
f
⇒
Re
D
{\displaystyle f\Rightarrow {{\operatorname {Re} }_{D}}}
لولهای داریم به قطر D و طول L که روغن با چگالی ρ و لزجت μ در آن جریان دارد. افت فشار لوله را به دست آورید (دبی حجمی Q).
V
=
Q
A
{\displaystyle V={\frac {Q}{A}}}
R
e
D
=
ρ
V
D
μ
{\displaystyle {{Re}_{D}}={\frac {\rho VD}{\mu }}}
با فرض رینولدز قطر کمتر از ۲۳۰۰ جریان لایهای و فرمول زیر صادق است:
F
=
64
R
e
D
{\displaystyle F={\frac {64}{{Re}_{D}}}}
Δ
p
=
ρ
h
f
g
{\displaystyle \Delta p=\ \rho {{h}_{f}}g}
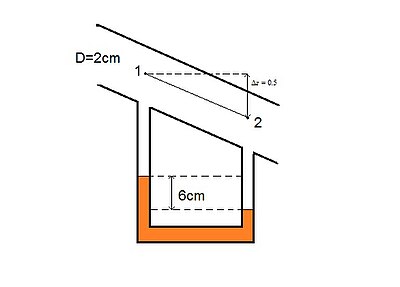
در شکل زیر سرعت کل را بدست آورید؟ (فاصله بین نقطه 1 و 2 برابر 2 متر است)
ker
o
s
e
n
e
⇔
[
μ
=
1.6
×
10
−
3
S
G
k
=
0.81
]
{\displaystyle \ker osene\Leftrightarrow [{\frac {\mu =1.6\times {{10}^{-3}}}{S{{G}_{k}}=0.81}}]}
چون در نقطه ی 2 ستون جیوه بیشتر پایین آمده ،پس جریان از 2 به 1 است.
p
2
−
p
1
ρ
g
+
(
z
2
−
z
1
)
=
f
1
l
v
2
2
D
g
⇒
v
1
=
v
2
{\displaystyle {\frac {{{p}_{2}}-{{p}_{1}}}{\rho g}}+({{z}_{2}}-{{z}_{1}})={{f}_{1}}{\frac {l{{v}^{2}}}{2Dg}}\Rightarrow {{v}_{1}}={{v}_{2}}}
از مانومتر داریم:
p
2
−
p
1
=
γ
w
[
(
S
G
m
−
S
G
k
)
Δ
h
+
Δ
z
S
G
k
]
{\displaystyle {{p}_{2}}-{{p}_{1}}={{\gamma }_{w}}[(S{{G}_{m}}-S{{G}_{k}})\Delta h+\Delta zS{{G}_{k}}]}
از جایگذاری این رابطه در رابطه ی بالا داریم:
γ
w
[
Δ
z
S
G
k
+
Δ
h
(
S
G
m
−
S
G
k
)
]
γ
w
S
G
k
+
Δ
z
=
f
1
×
2
v
2
0.02
×
2
×
g
⇒
f
v
2
=
0.155
{\displaystyle {\frac {{{\gamma }_{w}}[\Delta zS{{G}_{k}}+\Delta h(S{{G}_{m}}-S{{G}_{k}})]}{{{\gamma }_{w}}S{{G}_{k}}}}+\Delta z={{f}_{1}}\times {\frac {2{{v}^{2}}}{0.02\times 2\times g}}\Rightarrow f{{v}^{2}}=0.155}
ابتدا یک f حدس می زنیم : f=0.025
و از حلقه ی زیر به سرعت کل میرسیم:
f
1
→
v
1
=
2.49
→→
Re
D
=
ρ
v
D
μ
=
2.12
×
10
4
→
ε
D
=
0.025
→
f
2
=
0.0305
f
2
→
v
2
=
2.25
→→
Re
D
=
1.92
×
10
4
→
f
3
=
0.03
→
v
3
=
2.27
{\displaystyle {\begin{aligned}&{{f}_{1}}\to {{v}_{1}}=2.49\to \to {{\operatorname {Re} }_{D}}={\frac {\rho vD}{\mu }}=2.12\times {{10}^{4}}\to {\frac {\varepsilon }{D}}=0.025\to {{f}_{2}}=0.0305\\&{{f}_{2}}\to {{v}_{2}}=2.25\to \to {{\operatorname {Re} }_{D}}=1.92\times {{10}^{4}}\to {{f}_{3}}=0.03\to {{v}_{3}}=2.27\\\end{aligned}}}
پس سرعت کل برابر است با:2.27m/s
اگر داشته باشیم:
D
=
1
16
i
n
L
=
10
f
t
s
e
a
b
o
w
:
{
ρ
=
1.7
s
l
u
g
/
f
t
2
μ
=
2
×
10
−
3
l
b
f
.
s
/
f
t
2
}
Q
=
0.01
g
p
m
{\displaystyle {\begin{aligned}&D={\frac {1}{16}}in\\&L=10ft\\&sea~~~bow:\left\{\rho =1.7slug/f{{t}^{2}}~~~~~~~~~~~~~~\mu =2\times {{10}^{-3}}lbf.s/f{{t}^{2}}\right\}\\&Q=0.01gpm\\&\\&\\\end{aligned}}}
تغییرات فشار را بیابید.
Q
=
0.01
×
0.00233
=
2.33
×
10
−
4
f
t
3
/
s
V
=
Q
A
=
2.33
π
4
(
1
16
×
1
12
)
=
1.05
f
t
/
s
Re
D
=
ρ
V
D
μ
=
4.68
f
=
64
Re
D
=
13.67
h
f
=
f
L
D
V
2
2
g
=
450
f
t
Δ
P
=
h
f
×
ρ
g
=
28.6
×
10
3
l
b
f
/
f
t
2
=
172
p
s
i
{\displaystyle {\begin{aligned}&Q=0.01\times 0.00233=2.33\times {{10}^{-4}}f{{t}^{3}}/s\\&V={\frac {Q}{A}}={\frac {2.33}{{\frac {\pi }{4}}({\frac {1}{16}}\times {\frac {1}{12}})}}=1.05ft/s~~~~~~~~~~~~~~~~~~~~~~~\\&{{\operatorname {Re} }_{D}}={\frac {\rho VD}{\mu }}=4.68~~~~~~~~~~~~~~~~~~~~~f={\frac {64}{{\operatorname {Re} }_{D}}}=13.67\\&{{h}_{f}}=f{\frac {L}{D}}{\frac {{V}^{2}}{2g}}=450ft\\&\Delta P={{h}_{f}}\times \rho g=28.6\times {{10}^{3}}lbf/f{{t}^{2}}=172psi\\\end{aligned}}}
ρ
=
1000
k
g
m
3
μ
=
0.001
D
=
5
c
m
L
=
20
m
{\displaystyle {\begin{matrix}\rho =1000{\frac {kg}{{m}^{3}}}&\mu =0.001&D=5cm&L=20m\\\end{matrix}}}
k
1
=
0.5
k
2
=
1
k
3
=
10
{\displaystyle {\begin{matrix}{{k}_{1}}=0.5&{{k}_{2}}=1&{{k}_{3}}\\\end{matrix}}=10}
p
1
ρ
g
+
v
1
2
2
g
+
z
1
=
p
2
ρ
g
+
v
2
2
2
g
+
z
2
+
h
f
{\displaystyle {\frac {{p}_{1}}{\rho g}}+{\frac {v_{1}^{2}}{2g}}+{{z}_{1}}={\frac {{p}_{2}}{\rho g}}+{\frac {v_{2}^{2}}{2g}}+{{z}_{2}}+{{h}_{f}}}
h
f
=
∑
i
=
1
n
f
L
i
D
i
.
v
i
2
2
g
+
∑
j
=
1
n
k
j
.
v
j
2
2
g
{\displaystyle {{h}_{f}}=\sum \limits _{i=1}^{n}{f}{\frac {{L}_{i}}{{D}_{i}}}.{\frac {v_{i}^{2}}{2g}}+\sum \limits _{j=1}^{n}{{k}_{j}}.{\frac {v_{j}^{2}}{2g}}}
h
f
=
f
L
D
.
v
2
2
g
+
(
k
1
+
k
2
+
k
3
)
v
2
2
g
{\displaystyle {{h}_{f}}=f{\frac {L}{D}}.{\frac {{v}^{2}}{2g}}+\left({{k}_{1}}+{{k}_{2}}+{{k}_{3}}\right){\frac {{v}^{2}}{2g}}}
v
2
2
g
(
f
.
L
D
+
k
1
+
k
2
+
k
3
)
=
z
1
−
z
2
=
10
{\displaystyle {\frac {{v}^{2}}{2g}}\left(f.{\frac {L}{D}}+{{k}_{1}}+{{k}_{2}}+{{k}_{3}}\right)={{z}_{1}}-{{z}_{2}}=10}
v
2
(
4000
f
+
12.5
)
=
200
{\displaystyle {{v}^{2}}\left(4000f+12.5\right)=200}
Re
=
ρ
v
D
μ
=
50000
v
{\displaystyle \operatorname {Re} ={\frac {\rho vD}{\mu }}=50000v}
f
=
0.03
v
2
=
1.2
m
s
Re
=
60000
{\displaystyle {\begin{matrix}f=0.03&{{v}_{2}}=1.2{\frac {m}{s}}&\operatorname {Re} =60000\\\end{matrix}}}
f
=
0.0024
v
2
=
1.36
m
s
Re
=
68000
{\displaystyle {\begin{matrix}f=0.0024&{{v}_{2}}=1.36{\frac {m}{s}}&\operatorname {Re} =68000\\\end{matrix}}}
f
=
0.0235
v
2
=
1.88
m
s
Re
=
67600
{\displaystyle {\begin{matrix}f=0.0235&{{v}_{2}}=1.88{\frac {m}{s}}&\operatorname {Re} =67600\\\end{matrix}}}
→
f
=
0.0235
Q
=
1.88
A
{\displaystyle \to {\begin{matrix}f=0.0235&Q=1.88A\\\end{matrix}}}
ρ
=
1000
k
g
m
3
μ
=
0.001
L
=
20
m
H
=
10
m
{\displaystyle {\begin{matrix}\rho =1000{\frac {kg}{{m}^{3}}}&\mu =0.001&L=20m&H=10m\\\end{matrix}}}
ε
D
=
0.001
m
m
k
1
=
0.5
k
2
=
1
k
3
=
10
{\displaystyle {\begin{matrix}{\frac {\varepsilon }{D}}=0.001mm&{{k}_{1}}=0.5&{{k}_{2}}=1&{{k}_{3}}\\\end{matrix}}=10}
D
=
?
{\displaystyle D=?}
p
1
ρ
g
+
v
1
2
2
g
+
z
1
=
p
2
ρ
g
+
v
2
2
2
g
+
z
2
+
h
f
{\displaystyle {\frac {{p}_{1}}{\rho g}}+{\frac {v_{1}^{2}}{2g}}+{{z}_{1}}={\frac {{p}_{2}}{\rho g}}+{\frac {v_{2}^{2}}{2g}}+{{z}_{2}}+{{h}_{f}}}
h
f
=
f
L
D
.
v
2
2
g
+
(
k
1
+
k
2
+
k
3
)
v
2
2
g
{\displaystyle {{h}_{f}}=f{\frac {L}{D}}.{\frac {v_{}^{2}}{2g}}+\left({{k}_{1}}+{{k}_{2}}+{{k}_{3}}\right){\frac {v_{}^{2}}{2g}}}
v
2
2
g
(
f
L
D
+
k
1
+
k
2
+
k
3
)
=
z
1
−
z
2
→
v
=
Q
π
D
2
4
f
.
20
D
+
12.5
=
250000000
D
5
{\displaystyle {\frac {{v}^{2}}{2g}}\left(f{\frac {L}{D}}+{{k}_{1}}+{{k}_{2}}+{{k}_{3}}\right)={{z}_{1}}-{{z}_{2}}{\xrightarrow {v={\frac {Q}{\frac {\pi {{D}^{2}}}{4}}}}}f.{\frac {20}{D}}+12.5=250000000{{D}^{5}}}
Re
=
ρ
v
D
μ
=
260
D
{\displaystyle \operatorname {Re} ={\frac {\rho vD}{\mu }}={\frac {260}{D}}}
D
=
0.017
Re
=
15000
f
=
0.027
{\displaystyle {\begin{matrix}D=0.017&\operatorname {Re} =15000&f=0.027\\\end{matrix}}}
D
=
0.0205
Re
=
13000
f
=
0.029
{\displaystyle {\begin{matrix}D=0.0205&\operatorname {Re} =13000&f=0.029\\\end{matrix}}}
→
D
=
0.02
{\displaystyle \to D=0.02}
∑
Q
o
u
t
=
0
{\displaystyle \sum \limits _{}^{}{{Q}_{out}}=0}
در شکل زیر سرعت v2 را بیابید.
این مسئله از نوع مسائل نوع دوم است بنابراین f را حدس میزنیم.
البته در اینجا f را لایه ای فرض میکنیم وبا این فرض حل میکنیم.
z
1
−
(
V
2
2
g
+
z
2
)
=
h
f
+
h
m
=
f
L
D
V
2
2
2
g
+
k
V
2
2
2
g
f
=
64
Re
D
=
64
μ
ρ
V
2
D
1.2
=
(
64
μ
╱
ρ
V
2
D
+
k
+
1
)
V
2
2
2
g
=
(
k
+
1
2
g
)
V
2
2
+
32
μ
V
2
ρ
g
D
2
→
V
2
=
−
12.8
±
12.8
2
+
4
×
0.075
×
1.2
2
×
0.075
=
0.066
Re
D
=
ρ
V
D
μ
=
33
<
2300
→
L
a
min
a
r
{\displaystyle {\begin{aligned}&{{z}_{1}}-\left({\frac {{V}^{2}}{2g}}+{{z}_{2}}\right)={{h}_{f}}+{{h}_{m}}=f{\frac {L}{D}}{\frac {\mathop {V} _{2}^{2}}{2g}}+{\frac {k\mathop {V} _{2}^{2}}{2g}}\\&f={\frac {64}{{\operatorname {Re} }_{D}}}={\frac {64\mu }{\rho {{V}_{2}}D}}\\&1.2=\left({}^{64\mu }\!\!\diagup \!\!{}_{\rho V{}_{2}D}\;+k+1\right){\frac {V_{2}^{2}}{2g}}=\left({\frac {k+1}{2g}}\right)V_{2}^{2}+{\frac {32\mu {{V}_{2}}}{\rho g{{D}^{2}}}}\\&\to {{V}_{2}}={\frac {-12.8\pm {\sqrt {{{12.8}^{2}}+4\times 0.075\times 1.2}}}{2\times 0.075}}=0.066\\&{{\operatorname {Re} }_{D}}={\frac {\rho VD}{\mu }}=33<2300\to La\min ar\\\end{aligned}}}
از انجا که حاصل کمتر از2300 شده بنابراین فرض لایه ای بودن جریان درست بوده است.
در شکل زیر Q1 و Q2 را بیابید.
Q
=
Q
1
+
Q
2
→
π
4
D
1
2
V
1
+
π
4
D
2
2
V
2
=
Q
t
o
t
a
l
→
1
{\displaystyle Q={{Q}_{1}}+{{Q}_{2}}\to {\frac {\pi }{4}}{{D}_{1}}^{2}{{V}_{1}}+{\frac {\pi }{4}}{{D}_{2}}^{2}{{V}_{2}}={{Q}_{total}}\to 1}
اختلاف فشار نقاط 1 و 2 با اختلاف فشار دو سر لوله ی بالا و پایین برابر است.
Δ
P
=
h
f
1
.
ρ
g
=
h
f
2
.
ρ
g
→
h
f
1
=
h
f
2
→
f
1
L
1
D
1
V
1
2
=
f
2
L
2
D
2
V
2
2
→
2
→
V
1
(
0.196
+
0.903
f
1
f
2
)
=
4
→
3
f
1
=
0.017
f
2
=
0.0145
→
3
V
1
=
3.41
m
╱
s
→
1
V
2
=
4.25
m
╱
s
→
Re
1
=
1.7
×
10
6
&
Re
2
=
4.25
×
10
6
→
m
o
o
d
y
→
f
1
=
0.0172
&
f
2
=
0.0145
{\displaystyle {\begin{aligned}&\Delta P=h{{f}_{1}}.\rho g=h{{f}_{2}}.\rho g\to h{{f}_{1}}=h{{f}_{2}}\to {{f}_{1}}{\frac {{L}_{1}}{{D}_{1}}}{{V}_{1}}^{2}={{f}_{2}}{\frac {{L}_{2}}{{D}_{2}}}{{V}_{2}}^{2}\to 2\\&\to {{V}_{1}}\left(0.196+0.903{\sqrt {\frac {{f}_{1}}{{f}_{2}}}}\right)=4\to 3\\&{{f}_{1}}=0.017\\&{{f}_{2}}=0.0145{\xrightarrow {3}}{{V}_{1}}=3.41{}^{m}\!\!\diagup \!\!{}_{s}\;{\xrightarrow {1}}{{V}_{2}}=4.25{}^{m}\!\!\diagup \!\!{}_{s}\;\\&\to {{\operatorname {Re} }_{1}}=1.7\times {{10}^{6}}\And {{\operatorname {Re} }_{2}}=4.25\times {{10}^{6}}\to moody\to {{f}_{1}}=0.0172\And {{f}_{2}}=0.0145\\\end{aligned}}}
از ان جا که حدس اولیه جواب تقریبا خوبی داده حلقه را تکرار نمیکنیم.
→
V
1
=
3.41
m
╱
s
&
V
2
=
4.25
m
╱
s
→
Q
1
=
0.668
m
3
╱
s
&
Q
2
=
3.34
m
3
╱
s
{\displaystyle {\begin{aligned}&\to {{V}_{1}}=3.41{}^{m}\!\!\diagup \!\!{}_{s}\;\And {{V}_{2}}=4.25{}^{m}\!\!\diagup \!\!{}_{s}\;\\&\to {{Q}_{1}}=0.668{}^{{m}^{3}}\!\!\diagup \!\!{}_{s}\;\And {{Q}_{2}}=3.34{}^{{m}^{3}}\!\!\diagup \!\!{}_{s}\;\\\end{aligned}}}
در شکل زیر اگر
μ
=
10
−
3
p
a
.
s
,
ρ
=
10
3
k
g
.
m
−
3
{\displaystyle \mu ={{10}^{-3}}pa.s,\rho =10{}^{3}kg.{{m}^{-3}}}
(
P
ρ
g
+
v
2
2
g
+
z
)
1
=
(
P
ρ
g
+
v
2
2
g
+
z
)
2
+
h
f
(
1
)
{\displaystyle {{({\frac {P}{\rho g}}+{\frac {{v}^{2}}{2g}}+z)}_{1}}={{({\frac {P}{\rho g}}+{\frac {{v}^{2}}{2g}}+z)}_{2}}+{{h}_{f}}(1)}
از طرفی میدانیم
h
f
=
f
.
L
D
.
v
2
2
g
(
2
)
{\displaystyle {{h}_{f}}=f.{\frac {L}{D}}.{\frac {{v}^{2}}{2g}}(2)}
1 و 2 نتیجه میدهد
1
,
2
→
Δ
z
=
v
2
2
g
(
1
+
f
L
D
)
=
1.2
{\displaystyle 1,2\to \Delta z={\frac {{v}^{2}}{2g}}(1+{\frac {fL}{D}})=1.2}
فرض میکنیم جریان لایهای است (بدلیل کوچک بودن ابعاد)
پس
f
=
64
Re
(
3
)
{\displaystyle f={\frac {64}{\operatorname {Re} }}(3)}
Re
=
ρ
v
D
μ
(
4
)
{\displaystyle \operatorname {Re} ={\frac {\rho vD}{\mu }}(4)}
1 و 2 و 3 و 4 نتیجه میدهد
v
2
2
g
(
1
+
64
μ
ρ
v
D
L
D
)
=
1.2
→
12.8
v
+
0.05
v
2
=
1.2
→
v
1
=
.093
,
v
2
=
−
256.1
{\displaystyle {\begin{aligned}&{\frac {{v}^{2}}{2g}}(1+{\frac {{\tfrac {64\mu }{\rho vD}}L}{D}})=1.2\to 12.8v+0.05{{v}^{2}}=1.2\to \\&{{v}_{1}}=.093,{{v}_{2}}=-256.1\\\end{aligned}}}
جواب منفی غلط میباشد
پس
v
=
.093
{\displaystyle {v}=.093}
چون
Re
=
ρ
v
D
μ
=
5
×
10
2
⟨
2300
{\displaystyle \operatorname {Re} ={\frac {\rho vD}{\mu }}=5\times {{10}^{2}}\langle 2300}
پس فرض لایهای بودن درست میباشد و سرعت حاصل جواب مسئله است.
در شکل جریان دایمی و تراکم ناپذیر می باشد؛ توان پمپ را بیابید؟
و چون هر دو در سطح آزادند فشار هر دو برابر فشار اتمسفر است و سرعت هر دو نیز صفر است.
(
P
ρ
g
+
V
2
2
g
+
Z
)
1
+
h
p
=
(
P
ρ
g
+
V
2
2
g
+
Z
)
2
+
h
f
+
∑
h
m
{
P
1
=
P
2
V
1
=
V
2
}
{\displaystyle {\begin{aligned}&{{\left({\frac {P}{\rho g}}+{\frac {{V}^{2}}{2g}}+Z\right)}_{1}}+{{h}_{p}}={{\left({\frac {P}{\rho g}}+{\frac {{V}^{2}}{2g}}+Z\right)}_{2}}+{{h}_{f}}+\sum {{h}_{m}}\\&\left\{{\begin{aligned}&{{P}_{1}}={{P}_{2}}\\&{{V}_{1}}={{V}_{2}}\\\end{aligned}}\right\}\\\end{aligned}}}
حال با سادهسازی روابط داریم.
h
p
=
(
Z
2
−
Z
1
)
+
f
L
D
V
2
2
g
+
(
K
i
+
K
V
+
K
b
+
K
f
)
V
2
2
g
V
=
Q
A
=
10.23
f
t
s
⇒
Re
=
1.42
∗
10
4
ε
D
=
0.001
{\displaystyle {\begin{aligned}&{{h}_{p}}=\left({{Z}_{2}}-{{Z}_{1}}\right)+f{\frac {L}{D}}{\frac {{V}^{2}}{2g}}+\left({{K}_{i}}+{{K}_{V}}+{{K}_{b}}+{{K}_{f}}\right){\frac {{V}^{2}}{2g}}\\&V={\frac {Q}{A}}=10.23{\frac {ft}{s}}\Rightarrow \operatorname {Re} =1.42*{{10}^{4}}\\&{\frac {\varepsilon }{D}}=0.001\\\end{aligned}}}
اکنون با استفاده از رینولدز و ضریب سختی از نمودار مودی F را می خوانیم.
F=0.031
h
p
=
10
(
0.031
∗
40
2
12
+
0.5
+
5
+
0.9
+
1
)
10.23
2
2
∗
32.2
=
34.1
{\displaystyle {{h}_{p}}=10\left(0.031*{\frac {40}{\frac {2}{12}}}+0.5+5+0.9+1\right){\frac {{10.23}^{2}}{2*32.2}}=34.1}
حالا باh توان را محاسبه میکنیم.
P
=
ρ
g
h
p
Q
=
408
f
t
l
b
f
s
{\displaystyle P=\rho g{{h}_{p}}Q=408ft{\frac {lbf}{s}}}
دو مخزن به وسیله لولههایی از جنس چدن چکشخوار به طول 20 ft به یکدیگر متصل هستند. ورودی و خروجی لبه نیز تیز است. با فرض آن که سیال آب 20 درجه سانتیگراد و مخزن 1، 50ft نسبت به مخزن 2 بالاتر باشد با افزودن افتهای موضعی، دبی جریان را بر حسب فوت مکعب در ثانیه بیابید؟
حل
برای چدن چکش خوار داریم:
ε
=
0.0018
{\displaystyle \varepsilon =0.0018}
ورودی لبه تیز :
k
1
=
0.5
{\displaystyle k_{1}=0.5}
در اثر انبساط ناگهانی :
k
2
=
(
1
−
0.5
2
)
→
k
2
=
0.75
{\displaystyle k_{2}=(1-0.5^{2})\to k_{2}=0.75}
خروجی لبه تیز :
k
3
=
1
{\displaystyle k_{3}=1}
Q
=
V
a
A
a
=
V
a
(
π
4
D
a
2
)
=
V
b
A
b
=
V
b
(
π
4
D
b
2
)
→
V
b
=
1
4
V
a
Δ
Z
=
h
f
a
+
Σ
h
m
a
+
h
f
b
+
Σ
h
m
b
=
V
a
2
2
g
(
f
a
L
a
D
a
+
0.5
+
0.75
)
+
V
b
2
2
g
(
f
b
L
b
D
b
+
1
)
Δ
Z
=
50
=
V
a
2
2
(
32.2
)
(
f
a
×
240
+
1.25
+
f
b
120
16
+
1
16
)
{\displaystyle {\begin{aligned}&Q=V_{a}A_{a}=V_{a}({\frac {\pi }{4}}D_{a}^{2})=V_{b}A_{b}=V_{b}({\frac {\pi }{4}}D_{b}^{2})\to V_{b}={\frac {1}{4}}V_{a}\\&\Delta Z=h_{f_{a}}+\Sigma h_{m_{a}}+h_{f_{b}}+\Sigma h_{m_{b}}={\frac {V_{a}^{2}}{2g}}(f_{a}{\frac {L_{a}}{D_{a}}}+0.5+0.75)+{\frac {V_{b}^{2}}{2g}}(f_{b}{\frac {L_{b}}{D_{b}}}+1)\\&\Delta Z=50={\frac {V_{a}^{2}}{2(32.2)}}(f_{a}\times 240+1.25+f_{b}{\frac {120}{16}}+{\frac {1}{16}})\\\end{aligned}}}
مقدار
f
a
≅
f
b
≅
0.02
{\displaystyle f_{a}\cong f_{b}\cong 0.02}
V
a
≈
23.0
f
t
/
s
Re
a
≅
178000
f
a
≈
0.0238
{\displaystyle {\begin{aligned}&V_{a}\approx 23.0ft/s\\&\operatorname {Re} _{a}\cong 178000\\&f_{a}\approx 0.0238\\\end{aligned}}}
و همچنین :
V
b
≈
5.76
f
t
/
s
Re
b
≅
88800
f
b
≈
0.0221
{\displaystyle {\begin{aligned}&V_{b}\approx 5.76ft/s\\&\operatorname {Re} _{b}\cong 88800\\&f_{b}\approx 0.0221\\\end{aligned}}}
نهایتا داریم:
f
a
=
0.0239
f
b
=
0.0223
V
a
=
21.4
f
t
/
s
Q
=
21.4
(
π
4
)
(
1
12
)
2
=
0.117
f
t
3
/
s
{\displaystyle {\begin{aligned}&f_{a}=0.0239\\&f_{b}=0.0223\\&V_{a}=21.4ft/s\\&Q=21.4({\frac {\pi }{4}})({\frac {1}{12}})^{2}=0.117ft^{3}/s\\&\\\end{aligned}}}

























































![{\displaystyle \ker osene\Leftrightarrow [{\frac {\mu =1.6\times {{10}^{-3}}}{S{{G}_{k}}=0.81}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4346cd5dc685f4b0a481af52a2e0c3bffbe4f14)

![{\displaystyle {{p}_{2}}-{{p}_{1}}={{\gamma }_{w}}[(S{{G}_{m}}-S{{G}_{k}})\Delta h+\Delta zS{{G}_{k}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7570760d6353a94cbe1956b4c6e18c5c43ce402d)
![{\displaystyle {\frac {{{\gamma }_{w}}[\Delta zS{{G}_{k}}+\Delta h(S{{G}_{m}}-S{{G}_{k}})]}{{{\gamma }_{w}}S{{G}_{k}}}}+\Delta z={{f}_{1}}\times {\frac {2{{v}^{2}}}{0.02\times 2\times g}}\Rightarrow f{{v}^{2}}=0.155}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d848580f301bb49df6458123e495e25c9e78cef)


















































