بقای تکانه ی زاویه ای

تکانه زاویه ای در مکانیک کلاسیک

تکانهٔ زاویه‌ای یک ذره

تکانهٔ زاویه‌ای یک ذره به صورت ضرب خارجی بردارهای r {\displaystyle \mathbf {r} } {\displaystyle \mathbf {r} } (بردار مکان ذره نسبت به نقطهٔ مرجع) و تکانهٔ خطی p = m v {\displaystyle \mathbf {p} =m\mathbf {v} } {\displaystyle \mathbf {p} =m\mathbf {v} } تعریف می‌شود:

   L = r × p {\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} \,\!} {\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} \,\!}

وابستگی تکانهٔ زاویه‌ای به سرعت، جرم و توزیع جرم (موقعیت ذره نسبت به نقطهٔ مرجع) در رابطهٔ بالا مشهود است. بنا به تعریف، ضرب خارجی دو بردار شبه برداری است که بر هر دو بردار اصلی عمود است. پس، بردار تکانهٔ زاویه‌ای بر صفحهٔ دوران ذره عمود خواهد بود (شکل روبرو).

بنا به تعریف ضرب خارجی، تکانهٔ زاویه‌ای ذره را می‌توان به شکل زیر نیز نوشت:

   L = r × p = r m v sin ⁡ ( θ ) {\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} =rmv\sin {(\theta )}\,\!} {\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} =rmv\sin {(\theta )}\,\!}

که در آن، θ {\displaystyle \theta } \theta زاویهٔ بین بردارهای مکان و سرعت است. با توجه به رابطهٔ بالا، یکای اندازه‌گیری تکانهٔ زاویه‌ای در دستگاه SI به صورت kg. m. m/s یا N. m. s و یا j. sec خواهد بود. تکانهٔ زاویه‌ای سامانه بس ذره‌ای

اگر سامانه شامل بیش از یک ذره باشد، تکانهٔ زاویه‌ای آن حول یک نقطه را می‌توان با جمع بستن تکانهٔ زاویه‌ای تک تک ذرات تشکیل دهندهٔ سامانه حول همان نقطه به دست آورد. به فرض آن که سامانه دارای N {\displaystyle N} N ذره باشد، داریم:

   L = ∑ i = 1 N L i = ∑ i = 1 N r i × m i v i {\displaystyle \mathbf {L} =\sum _{i=1}^{N}\mathbf {L} _{i}=\sum _{i=1}^{N}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}\,\!} {\displaystyle \mathbf {L} =\sum _{i=1}^{N}\mathbf {L} _{i}=\sum _{i=1}^{N}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}\,\!}

که در آن، r i {\displaystyle \mathbf {r} _{i}} {\displaystyle \mathbf {r} _{i}} مکان ذرهٔ i {\displaystyle i} iام نسبت به نقطهٔ مرجع، m i {\displaystyle m_{i}} {\displaystyle m_{i}} جرم ذره و v i {\displaystyle \mathbf {v} _{i}} {\displaystyle \mathbf {v} _{i}} سرعت آن است.

بقای تکانه ی زاویه ای(angular momentum)

دیدیم که بردار گشتاور نیرو به صورت مشتق زمانی بردار اندازه حرکت زاویه‌ای است. این رابطه شبیه رابطه ای است که برای قانون دوم نیوتن نوشتیم. در آنجا نیرو کمیتی است که باعث حرکت انتقالی جسم می‌شود، لذا نیرو با مشتق زمانی اندازه حرکت خطی برابر است. در اینجا نیز گشتاور نیرو سبب دوران جسم می‌شود و لذا به صورت مشتق زمانی اندازه حرکت زاویه‌ای تعریف می‌شود.

مراحل حل مساله بقای تکانه زاویه ای:

1. مشخص کردن حجم کنترل مناسب
2. نوشتن معادله بقای جرم
3. قراردادن دستگاه در محل مناسب(1. در نقطه ای دستگاه مختصات را قرار می دهیم که گشتاور را در آن نقطه بخواهند 2.یا این که در خود سوال به ما محل دستگاه را داده باشد.)
4. چون بردارrوv باید ضرب خارجی شوند ابتدا آنها را به صورت برداری می نویسیم
5. معادله بقای تکانه زاویه ای را می نویسیم.

نکته: در این جا هم مثل بقای تکانه خطی سرعت V همان سرعت مطق سیال نسبت به دستگاه انتخابی می باشد

نکته: بهتر است دستگاه را لخت بگیریم تا محاسبات ما ساده شود زیرا اگر دستگاه را غیرلخت بگیریم شتاب کریولیس در معادله ظاهر می شود.

1. اگر سرعت زاویه حجم کنترل نسبت به دستگاه صفر یا ثابت باشد مشتق زمانی آن نیز صفر خواهد شد و معدلات ما ساده تر خواهد شد.
2. نیروهای خارجی را مشخص می کنیم و گشتاور آن ها را نسبت به مبدا مختصات می گیریم.

نتایج استفاده از قانون بقای تکانه زاویه ای:
از آنجا که کمیت اندازه حرکت زاویه‌ای، یک کمیت برداری است، لذا ثابت بودن یا پایسته بودن آن مستلزم ثابت بودن مقدار و جهت آن می‌باشد. ثابت بودن مقدار آن که در روابط اعمال می‌شود، اما ثابت بودن جهت بردار اندازه حرکت زاویه‌ای مستلزم آن است که حرکت در صفحه صورت گیرد، یعنی چون جهت بردار اندازه حرکت اندازه حرکت زاویه‌ای را با استفاده از قاعده دست راست در جهت عمود بر صفحه شامل بردار مکان و بردار سرعت تعریف کردیم، لذا پیامد ثابت بودن جهت محدود شدن حرکت به صفحه خواهد بود.

ازمعادله ی بقای تکانه ی زاویه ای برای بدست آوردن گشتاورهای موجود در حجم کنترل استفاده می شود. فرم کلی معادله به صورت ذیل می باشد:

${\frac {\partial \;}{\partial \;t}}(m{\vec {r}}\times {\vec {v}})_{c.v}=({\dot {m}}{\vec {r}}\times {\vec {v}})_{in}-({\dot {m}}{\vec {r}}\times {\vec {v}})_{out}+\sum ({\vec {M}})_{o}$

توضیحات:

1- سرعت بدست آمده ازقانون بقای جرم سرعتی سیال نسبت به حجم کنترل در نظر گرقته شده است.

نکته : فرمول بالا درواقع بیان کننده رابطه زیر است : 

 ('نرخ تولید')+('نرخ خروجی')-('نرخ ورودی') =c.v('نرخ تغییرات')
 
                                                                                             

توجه شود که نرخ تولید در اینجا همان ممان(گشتاور) است

---

نکته : در یک سامانه بسته، تکانهٔ زاویه‌ای کل سامانه با گذشت زمان ثابت می‌ماند. پایستگی تکانهٔ زاویه‌ای نتیجهٔ همسانگردی فضاست.

مثال 1

در شکل زیر سیالی با چگالی ρ از تکیه‌گاه وارد لوله می‌شود و با سرعت V₀ از لوله خارج می‌شود ،نیرو و گشتاور وارد بر تکیه‌گاه را محاسبه کنید؟

فرض میکنیم که شرایط پایدار است

بقای جرم:

$\partial {\frac {{m}_{c.v.}}{\partial t}}={{\dot {m}}_{in}}-{{\dot {m}}_{out}}\Rightarrow \rho A{{v}_{in}}=\rho A{{v}_{out}}\Rightarrow {{v}_{in}}={{v}_{out}}={{v}_{0}}$

بقای تکانه خطی در راستای محور x

$\partial {\frac {{\left(m{{v}_{x}}\right)}_{c.v}}{\partial t}}={{\left({\dot {m}}{{v}_{x}}\right)}_{in}}-{{\left({\dot {m}}{{v}_{x}}\right)}_{out}}+\sum \limits _{}^{}{{F}_{x}}\Rightarrow {{F}_{x}}=\rho A{{v}_{0}}^{2}$

کل وزن مجموعه برابر است با :

${{W}_{1}}={{W}_{2}}=\rho gLA\Rightarrow {{W}_{total}}=2\rho gLA$

بقای تکانه خطی در راستای محور y

${\begin{aligned}&\partial {\frac {{\left(m{{v}_{y}}\right)}_{c.v}}{\partial t}}={{\left({\dot {m}}{{v}_{y}}\right)}_{in}}-{{\left({\dot {m}}{{v}_{y}}\right)}_{out}}+\sum \limits _{}^{}{{F}_{y}}\\&\Rightarrow {{F}_{y}}-{{W}_{total}}=-{\dot {m}}{{v}_{0}}\Rightarrow {{F}_{y}}=\rho A\left(2gL-{{v}_{0}}^{2}\right)\\\end{aligned}}$

نکته :رابطه ی بدست امده نشان دهنده ان است که اگر سرعت زیاد شود جسم معلق باقی میماند

بقای تکانه ی زاویه ای حول محور عمود بر صفحه:

${\begin{aligned}&\partial {\frac {{\left(m{\vec {r}}\times {\vec {v}}\right)}_{c.v.}}{\partial t}}={{\left({\dot {m}}{\vec {r}}\times {\vec {v}}\right)}_{in}}-{{\left({\dot {m}}{\vec {r}}\times {\vec {v}}\right)}_{out}}+\sum \limits _{}^{}{{\vec {M}}_{o}}\\&\left\{{\begin{aligned}&{{\left({\dot {m}}{\vec {r}}\times {\vec {v}}\right)}_{out}}=-{\dot {m}}L{{v}_{0}}{\hat {k}}=-\rho AL{{v}_{o}}^{2}{\hat {k}}\\&\sum \limits _{}^{}{{{\vec {M}}_{o}}={{T}_{o}}{\hat {k}}}-\rho gLA\left({\frac {L}{2}}\right){\hat {k}}-\rho gLAL{\hat {k}}\\\end{aligned}}\right.\Rightarrow {{T}_{o}}=\rho AL\left({\frac {3}{2}}g-{{v}_{o}}^{2}\right)\\\end{aligned}}$

---

مثال 2

در شکل زیر آب با دبی حجمی Q و چگالی ρ وارد لوله می شود و با سرعت V خارج می شود عکس العمل تکیه گاه را بیابید .

میخواهیم نیرو های تکیه گاهی R در راستاهای x و y و گشتاور حول نقطه تکیه گاهی (ناشی از عکس العمل تکیه گاه)را بدست آوریم:

در راستای x نیرویی وارد نمیشود لذا با استفاده از معادله زیر داریم:

$\sum F_{x}=0\Rightarrow \;R_{x}=0$

بقای جرم:

$({\dot {m}})_{in}=({\dot {m}})_{out}\Rightarrow \;Q=A_{out}V_{out}\Rightarrow \;V_{out}={\frac {Q}{A_{out}}}$

با استفاده از معادله بقای تکانه خطی نیروی R در راستای y را نیز محاسبه می نماییم :

$0={\dot {m}}v_{i}-({\dot {m}}(-v_{out}))+(-W+R_{y}+P_{i}A_{i})\Rightarrow \;R_{y}=-\rho Q^{2}({\frac {1}{A_{i}}}+{\frac {1}{A_{o}}})+(W-P_{i}A_{i})$

و در نهایت بقای تکانه زاویه ای در راستای z :

${\frac {\partial \;}{\partial \;t}}(m{\vec {r}}\times {\vec {v}})_{c.v}=({\dot {m}}{\vec {r}}\times {\vec {v}})_{in}-({\dot {m}}{\vec {r}}\times {\vec {v}})_{out}+\sum ({\vec {M}})_{o}$

$0=0-[{\dot {m}}(-Lv_{out})]+M_{o}+M_{w}$

که در آن

$M_{w}=g[-(\rho A_{o}L){\frac {L}{2}})-(\rho A_{o}{\frac {L}{2}})L]$

$\Rightarrow \;M_{o}=-\rho QLv_{out}+\rho AL^{2}g$

---

مثال 3

در شکل زیر آب با دبی حجمیQ وارد آب پاش شده و با سرعت v خارج می شود .

الف)چه گشتاوری در مبدا وارد شود تا آب پاش نچرخد؟

ب)اگر گشتاور T وارد شود سرعت زاویه ای آب پاش را محاسبه کنید .

ج)اگر T وارد نشود و جسم دارای شتاب باشد، شتاب زاویه ای $\alpha ={\frac {d\omega }{dt}}$ و سرعت زاویه ای چقدر است ؟


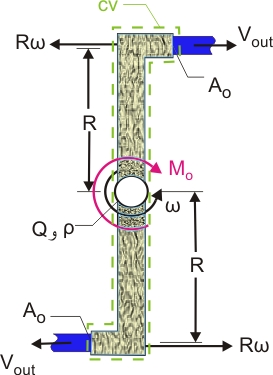
توجه 1 :حجم کنترل (Control Volume) همراه با آب پاش می چرخد.
توجه 2 :شرایط Steady State است .

حل قسمت الف :

بقای جرم :

${\frac {\partial \;m_{c.v}}{\partial \;t}}={\dot {m}}_{in}-{\dot {m}}_{out}\Rightarrow \;\rho Q=2\rho A_{o}v_{out}\Rightarrow \;v_{out}={\frac {\rho Q}{2\rho A_{o}}}$

بقای تکانه زاویه ای :

${\frac {\partial \;}{\partial \;t}}(m{\vec {r}}\times {\vec {v}})_{c.v}=({\dot {m}}{\vec {r}}\times {\vec {v}})_{in}-({\dot {m}}{\vec {r}}\times {\vec {v}})_{out}+\sum ({\vec {M}})_{o}$

$0=0+2{\dot {m}}Rv_{out}-M_{o}\Rightarrow \;M_{o}=2{\dot {m}}Rv_{out}$

حل قسمت ب:


بقای جرم:

${\dot {m}}_{in}={\dot {m}}_{out}\Rightarrow \;v_{out_{rel}}={\frac {Q}{2A_{o}}}$

بقای تکانه زاویه ای :

${\frac {\partial \;}{\partial \;t}}(m{\vec {r}}\times {\vec {v}})_{c.v}=({\dot {m}}{\vec {r}}\times {\vec {v}})_{in}-({\dot {m}}{\vec {r}}\times {\vec {v}})_{out}+\sum ({\vec {M}})_{o}$

$0=0+2{\dot {m}}R(v_{out_{rel}}-R\omega )-T$

از طرفی :

${\vec {V}}_{out_{rel}}={\vec {V}}_{out_{abs}}-{\vec {U}}\Rightarrow \;v_{out_{abs}}=({\frac {Q}{2A_{o}}}-R\omega )$

$\Rightarrow \;T=\rho QR({\frac {Q}{2A_{o}}}-R\omega )\Rightarrow \;\omega ={\frac {Q}{2A_{o}}}-{\frac {T}{2\rho Qr^{2}}}$

حل قسمت ج :

${\frac {\partial }{\partial t}}({\vec {r}}\times m{\vec {r\omega }})_{c.v}={\frac {\partial }{\partial }}\int \rho {\vec {r}}\times {\vec {r}}\times {\vec {\omega }}dv=\int rrdm\times {\frac {\partial \omega }{\partial t}}=I\alpha$

${\frac {\partial }{\partial t}}({\vec {r}}\times {\vec {m\omega }})_{c.v}=({\vec {r}}\times {\dot {m}}{\vec {v}})_{in}-({\vec {r}}\times {\dot {m}}{\vec {v}})_{out}+\sum M_{o}$

$I\alpha =I{\dot {\omega }}=\rho QR[{\frac {Q}{2A}}-R\omega ]$

${\dot {\omega }}=c_{1}-c_{2}\omega \Rightarrow \;\int _{0}^{\omega }{\frac {d\omega }{c_{1}-c_{2}\omega }}=\int _{0}^{t}dt$

$t={\frac {-1}{c_{2}}}[Ln{\frac {c_{1}-c_{2}\omega }{c_{1}}}]$

$if(t\rightarrow \;\infty )\Rightarrow \omega ={\frac {c_{1}}{c_{2}}}={\frac {Q}{2RA}}$

---

مثال 4

آب با دبی حجمی Q وارد فواره می شود.مقدار T را طوری بیابید که فواره نچرخد.

حجم کنترل و دستگاه مختصات را ساکن فرض می کنیم:

بقای جرم:

${{\dot {m}}_{in}}={{\dot {m}}_{out}}\to 2\rho A{{v}_{out-tel}}=\rho Q\to {{v}_{out-rel}}={\frac {Q}{2A}}$

بقای تکانه ی زاویه ای حول محور عمود بر صفحه:

$\partial {\frac {{(m{\vec {r}}\times {\vec {v}})}_{c.v.}}{\partial t}}={{({\dot {m}}{\vec {r}}\times {\vec {v}})}_{in}}-{{({\dot {m}}{\vec {r}}\times {\vec {v}})}_{out-rel}}+{{\sum {\vec {M}}}_{o}}$

پس داریم:

$\left\{{\begin{aligned}&{{({\dot {m}}{\vec {r}}\times {\vec {v}})}_{out}}=2(\rho A{{v}_{out-rel}})R{{v}_{out-rel}}{\hat {k}}\\&{{\sum {\vec {M}}}_{o}}=T{\hat {k}}\\\end{aligned}}\right.\to T=2\rho A{{v}_{out}}^{2}R={\frac {\rho {{Q}^{2}}}{2A}}R$

---