تشابه
تشابه
[ویرایش]یکی از کاربردهای تحلیل ابعادی در سیالات آن است که با توجه به نیاز مهندسان به شبیه سازی فرایندهای سینماتیکی و ... نیاز است تا اطلاعات اولیه ای را بدست آورده و در طراحی سیستم ها مورد توجه قرار داد. برای این کار نیاز است تا ابتدا و قبل از تولید انبوه بر روی یک نمونه به انجام آزمایش هایی دست زد. همچنین با توجه به محدودیت هایی همچون منابع مالی و کمبود قطعات و ... نمی توان بر روی نمونه اصلی آزمایش کرد. بر این اساس مهندسین نمونه و مدلی از سیستم را طراحی کرده و با توجه به علم تشابه به آزمایش های مورد نظر خود اقدام می کنند.
برای استفاده از این روش لازم است ابتدا تابعی بی بعد از روابط حاکم بر جسم بدست آورد. پس از این مرحله که دیگر روابط بین متغیرها شناخته شده است نسبت به تشابه گیری اقدام می شود. که بیان صوری چگونگی تشابه بدین قرار است که:
اگر تمام پارامترهای بی بعد مربوط به مدل و نمونه واقعی یکسان باشند آنگاه شرایط جریان برای آزمایش مدل کاملا مشابه است.
در متون و نوشته های مهندسی به جای تشابه کامل نمونه های خاصی از تشابه بررسی می شوند که رایج ترین آنها تشابه هندسی، سینماتیکی، دینامیکی و حرارتی می باشد.
تشابه در لوله ها
[ویرایش]
با بررسی پارامترها و بدست آوردن متغیرهای بی بعد در لوله ها ، معمولا سه متغیر بی بعد در لوله ها اهمیت دارند که مهمترین آنها عدد رینولدز ( Reynolds Number ) است . همانطور که گفته شده باید متغیر های بی بعد در مدل و نمونه اصلی برابر باشند، لذا عدد رینولدز که خودش یک متغیر بی بعد مهم است نیز باید در مدل و نمونه ی اصلی برابر باشد . بنابراین داریم :
حال فرض کنید که با داشتن لزجت ، چگالی و قطر لوله (D) در مدل و نمونه ی اصلی و سرعت در مدل ، می خواهیم سرعت در نمونه ی اصلی را به دست آوریم . لذا داریم :
تشابه در لایه مرزی
[ویرایش]تشابه در لایه مرزی:
معادله هیدرودینامیکی و گرمایی تشابه زیادی دارند.اگر شیب فشار در معادله هیدرودینامیکی و جمله اتلاف ویسکوز در معادله گرمایی ناچیز باشند ،این دو معادله شکل یکسانی خواهند داشت.
پارامتر های تشابه در لایه مرزی
برای بررسی تشابه ابتدا باید معادله های لایه مرزی را بی بعد کرد.برای این منظور،متغیر های بی بعد زیر را تعریف می کنیم.
در روابط بالا l طول مشخصه است و v سرعت جریان در فرادست است.
با صرف نظر از جمله اتلاف ویسکوز شکل بی بعد معادله های پایستاری به صورت زیر به دست می آید:
عدد رینولدز:
عدد پرانتل:
با استفاده از تعریف اعداد رینولدز و پرانتل همراه با معادله های لایه مرزی
و
معادله های تکانه و انرزی به صورت زیر در می آیند.
عدد پرانتل نسبت پخشندگی تکانه به پخشندگی انرژی گرمایی است ب عبارت دیگر ، آهنگ پخش تکانه در لایه مرزی هیدرودینامیکی را به آهنگ پخش انرژی در لایه مرزی گرمایی مقایسه می کند.
عدد پرانتل برای گاز ها نزدیک 1 است برای فلزات مایع خیلی کوچکتر از یک و برای روغن ها بسیار بیشتر از یک می باشد.
اگر دو جریان با شرایط متفاوت، پارامتر های تشابه یکسان و شرایط مرزی بی بعد یکسان داشته باشند، حل معادله های دیفرانسیل برای سرعت و دمای بی بعد نیز یکسان خواهد بود.
انواع تشابه
[ویرایش]
تشابه هندسی:
در تشابه هندسی بعد طول{L} مهم است و قبل از پرداختن به هر گونه آزمایش وجود این تشابه باید مشخص شود که تعریف آن چنین است:
یک مدل و نمونه واقعی،دارای تشابه هندسی هستند اگر و تنها اگر تمام ابعاد دو جسم در تمام مختصات سه گانه دارای یک نسبت مقیاس خطی باشند.به عبارتی دیگر نسبت ابعاد متناظر مدل و نمونه اصلی عدد ثابتی است.
به بیانی دیگر آنکه تمام زوایا و جهت های جریان در تشابه هندسی یکسانند و راستای مدل و نمونه واقعی باید نسبت به محیط اطراف همسان باشند.
توجه کنید که یکسان بودن تمام مقیاس های طولی ،مانند این است که از نمونه واقعی عکس بگیرد، و آن را تا رسیدن به اندازه مدل ،کوچک یا بزرگ کنید.اگر مدل یک دهم اندازه نمونه واقعی ساخته شده باشد ،طول ،عرض و ارتفاع نیز باید یک دهم اندازه نمونه واقعی در نظر گرفته شود.،و البته نه تنها این مختصات،بلکه تمام شکل باید یک دهم اندازه واقعی شود.«نقاط هم نظیر» از نظر فنی، نقطه هایی با موقعیت نسبی یکسانند،به عنوان مثال،دماغه یک نمونه واقعی هم نظیر دماغه مدل است و نوک بال چپ مدل متناظر خواهد بود.در این صورت ،تشابه هندسی ایجاب می کند که تمام نقاط متناظر با یک نسبت تشابه خطی به هم مربوط شوند.این شرط برای شکل هندسی سیال نیز همچون شکل هندسی مدل اعمال می شود.
شکل 5-4 ،یک بال واقعی و مدل با مقیاس یک دهم را نشان می دهد.تمام طول های مدل یک دهم نمونه واقعی است،اما «زاویه حمله» نسبت به جریان آزاد در هر دو یکسان است: ده درجه نه یک درجه تمام جزییات فیزیکی باید روی مدل مقیاس شود، برخی از آن ها دقت بیشتری لازم دارد و از بعضی دیگر می توان چشم پوشی کرد:
1- شعاع دماغه مدل باید یک دهم اندازه واقعی باشد،
2- زبری سطح مدل باید یک دهم اندازه واقعی باشد،
3- اگر در نمونه واقعی ،سیم 5 میلیمتری جابه جا کننده لایه مرزی،از «لبه حمله»، 1.5m فاصله داشته باشد،قطر سیم جابه جا کننده در مدل، باید 0.5mm و فاصله آن از لبه حمله نیز 15mm باشد ،
4- اگر در نمونه واقعی ، پرچ های برآمده به کار رفته باشد،در مدل نیز باید نوع یک دهم آن به کار رود.
هر گونه عدم رعایت این جزییات ،تشابه هندسی را نقض خواهد کرد و باید به کمک مقایسه تجربی ثابت کرد که این تفاوت روی رفتار نمونه واقعی تأثیر عمده ای نمی گذارد.
تشابه سینماتیکی:
اساس این تشابه داشتن نسبت تشابه طولی و زمانی یکسان است. یعنی نسبت تشابه سرعت باید برای هر دو یکسان باشد. این موضوع را لانگهار چنین بیان می کند:
حرکت دو سیستم در صورتی از نظر سینماتیکی شبیه است که ذرات متناظر در زمان های متناطر در نقاط متناظر قرار گرفته باشند.
نکته:اگر دو جریان از لحاظ سینماتیکی مشابه باشند از نظر هندسی هم مشابهند ولی عکس این موضوع الزاما برقرار نیست .
نکته:لازمه تشابه سینماتیکی یکسان بودن نوع جریان مدل و نمونه اصلی است.
تساوی مقیاس طولی ،به راحتی تشابه هندسی نیز در بر دارد، ولی تساوی مقیاس زمانی می تواند مفاهیم دینامیکی بیشتری مانند تساوی عدد رینولدز و ماخ را الزامی سازد.
در شکل 6-5 الف،حالت خاصی از جریان بدون اصطکاک تراکم ناپذیر و بدون سطح آزاد رسم شده است.این گونه جریان های سیال کامل با مقیاس های زمانی و طولی مستقل،بدون نیاز به پارامترهای اضافی ،تشابه سینماتیکی دارند.
تشابه دینامیکی:
بین مدل و نمونه واقعی هنگامی تشابه دینامیکی وجود دارد که نسبت مقیاس طول(L)، زمان(t)و نیرو (F) برای آنها مساوی باشد. در اینجا نیز تشابه هندسی شرط اول است و فقط هنگامی تشابه دینامیکی همزمان با تشابه سینماتیکی بر قرار خواهد بود که ضرایب فشار و نیرو برای مدل و نمونه واقعی یکسان باشد.
درصورتی که:
1. برای جریان تراکم پذیر: بایستی عدد رینولدز و ماخ و نسبت گرمای ویژه مدل و نمونه واقعی یکسان باشند.
2. برای جریان تراکم ناپذیر:
الف) بدون سطح آزاد بایستی اعداد رینولدز مدل و نمونه واقعی مساوی باشند.
ب) با سطح آزاد بایستی اعداد فرود و رینولدز و وبر و کاویتاسیون مدل و نمونه واقعی یکسان باشند.
نکته: برای برقراری تشابه دینامیکی بین دو جریان باید هر دو تشابه هندسی و سینماتیکی برقرار باشد.
اهميت وجود تشابه ديناميكي اينست كه اگر در سرتاسر جريان نسبت بين نيروهاي متناظر دو جريان يكسان باشد انتگرال توزيع اين نيروها (كه مي تواند مثلا
نيروي دراگ، شناوري، ... را بدست دهد) نيز براي جريان مدل و نمونه اصلي داراي همان نسبت بوده و مي توان از نتايج حاصل از آزمايش استفاده كرد.
برای تشابه دینامیکی باید کلیه اعداد بدون بعد برای مدل و نمونه اصلی برابر باشند.
در اکثر مسائل هندسی برقراری تساوی همه اعداد بی بعد لازم نیست چون برخی از نیروهای ذکر شده ممکن است 1) تاثیر نداشته باشند 2) بزرگی شان ناچیز باشد یا 3) در جهات مختلف چنان اثر کند که متقابلا حذف شود.
تشابه جرمي : يعني توزيع جرم به گونه اي باشد كه نسبت جرم مخصوص براي تمام جفت نقاط متناظر يكسان باشد.
با توجه به اينكه در تشابه سينماتيكي شتابها در نقاط متناظر موازي و داراي نسبت يكساني هستند، برآيند نيروهاي وارد بر ذرات متناظر موازي بوده و بدليل تشابه جرمي نسبت يكساني در تمام نقاط جريان دارند.
...............................................................
مثال1
[ویرایش]ظرفی مطابق شکل با سرعت v در حال حرکت است. با توجه به ابعاد مشخص شده روی شکل، مقدار F و را به دست آورید.
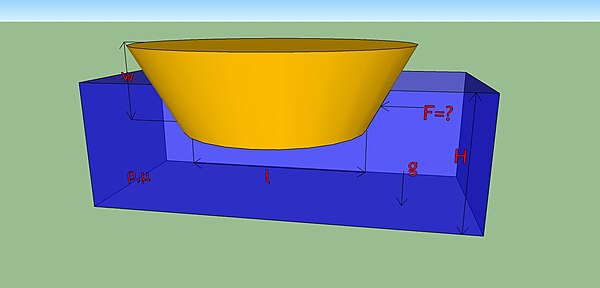
𝜌 ، l و v متغیرهای تکرار شونده هستند.
تعداد گروه های بدون بعد:
با استفاده از تشابه داریم:
در این مثال، 2 مقدار متفاوت برای به دست می آید که در این حالت معمولا از عدد رینولدز (Re) صرف نظر می کنیم.
...............................................................
مثال۲
[ویرایش]میخواهیم هواپیمای مادون صوت در هوای اتمسفریک با سرعت 100m/s پرواز کند. مدل در مقیاس ۱/۲۰ از آن تهیه کردیم و در تونل باد قرار دادهایم. سرعت جریان هوا در تونل باد چقدر باید باشد؟ در این شرایط آزمایش انجام دادهایم و نیرویی که به مدل وارد شده 10KN است نیروهای وارد بر مدل اصلی چقدر خواهد شد؟
هواپیما مدل سازی شده:
هواپیمای واقعی:
حل:
تشابه هندسی:
تشابه دینامیکی:
باتوجه به اینکه ثابت است
قسمت ب
در مثال ۲ اگر جریان تراکمپذیر باشد و داشته باشیم:
رابطه زیر را بدست آوردید؟
با توجه به دادههای بالا داریم:
نتیجه میگیریم که با سیال یکسان نمیتوان تشابه دینامیکی را بر قرار کرد.




















![{\displaystyle {\begin{aligned}&F=f(v,H,l,w,g,\rho ,\mu ),{\frac {{l}_{M}}{{l}_{P}}}=0.01,{\frac {{H}_{M}}{{H}_{P}}}=0.01,{\frac {{w}_{M}}{{w}_{P}}}=0.01,\\&[F]=ML{{T}^{-2}}\\&[v]=L{{T}^{-1}}\\&[H]=L\\&[l]=L\\&[w]=L\\&[g]=L{{T}^{-2}}\\&[\rho ]=M{{L}^{-3}}\\&[\mu ]=M{{L}^{-1}}{{T}^{-1}}\\&A=\left({\begin{matrix}F&v&H&l&w&g&\rho &\mu \\1&0&0&0&0&0&1&1\\1&1&1&1&1&1&-3&-1\\-2&-1&0&0&0&-2&0&-1\\\end{matrix}}\right){\begin{matrix}{}\\M\\L\\T\\\end{matrix}}\\&\Rightarrow n=8\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b1701dedb28a85607bd1f6da52aef22ca083513)

![{\displaystyle {\begin{aligned}&p=n-r=5\\&{{\Pi }_{1}}=[{\frac {F}{{{\rho }^{\alpha }}{{v}^{\beta }}{{l}^{\gamma }}}}]=1\Rightarrow {\frac {ML{{T}^{-2}}}{{{(M{{L}^{-3}})}^{\alpha }}{{(L{{T}^{-1}})}^{\beta }}{{(L)}^{\gamma }}}}=1{\overset {\alpha =1,\beta =2,\gamma =2}{\mathop {\Rightarrow } }}\,{{\Pi }_{1}}={\frac {F}{\rho {{v}^{2}}{{l}^{2}}}}\Rightarrow {{\Pi }_{1}}={{C}_{D}}\\&{{\Pi }_{2}}=[{\frac {H}{{{\rho }^{\alpha }}{{v}^{\beta }}{{l}^{\gamma }}}}]=1\Rightarrow {\frac {L}{{{(M{{L}^{-3}})}^{\alpha }}{{(L{{T}^{-1}})}^{\beta }}{{(L)}^{\gamma }}}}=1{\overset {\alpha =0,\beta =0,\gamma =1}{\mathop {\Rightarrow } }}\,{{\Pi }_{2}}={\frac {H}{l}}\\&{{\Pi }_{3}}=[{\frac {w}{{{\rho }^{\alpha }}{{v}^{\beta }}{{l}^{\gamma }}}}]=1\Rightarrow {\frac {L}{{{(M{{L}^{-3}})}^{\alpha }}{{(L{{T}^{-1}})}^{\beta }}{{(L)}^{\gamma }}}}=1{\overset {\alpha =0,\beta =0,\gamma =1}{\mathop {\Rightarrow } }}\,{{\Pi }_{3}}={\frac {w}{l}}\\&{{\Pi }_{4}}=[{\frac {g}{{{\rho }^{\alpha }}{{v}^{\beta }}{{l}^{\gamma }}}}]=1\Rightarrow {\frac {L{{T}^{-2}}}{{{(M{{L}^{-3}})}^{\alpha }}{{(L{{T}^{-1}})}^{\beta }}{{(L)}^{\gamma }}}}=1{\overset {\alpha =0,\beta =2,\gamma =-1}{\mathop {\Rightarrow } }}\,{{\Pi }_{4}}={\frac {g}{{{v}^{2}}{{l}^{-1}}}}={\frac {gl}{{v}^{2}}}\Rightarrow {{\Pi }_{4}}=Fr\\&{{\Pi }_{5}}=[{\frac {\mu }{{{\rho }^{\alpha }}{{v}^{\beta }}{{l}^{\gamma }}}}]=1\Rightarrow {\frac {M{{L}^{-1}}{{T}^{-1}}}{{{(M{{L}^{-3}})}^{\alpha }}{{(L{{T}^{-1}})}^{\beta }}{{(L)}^{\gamma }}}}=1{\overset {\alpha =1,\beta =1,\gamma =1}{\mathop {\Rightarrow } }}\,{{\Pi }_{2}}={\frac {\mu }{\rho vl}}={\frac {1}{\operatorname {Re} }}\\&{{\Pi }_{1=}}{{f}^{*}}({{\Pi }_{2}},{{\Pi }_{3}},{{\Pi }_{4}},{{\Pi }_{5}})\Rightarrow {{C}_{D}}={{f}^{*}}({\frac {H}{l}},{\frac {w}{l}},Fr,\operatorname {Re} )\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b55f25575ddd4676dedac92be088f03b976e326)









