ریاضیات برای اقتصاد/بهینهسازی ایستا
| مقدمه | بهینهسازی ایستا | ماتریسها |
| ریاضیات برای اقتصاد |
تعاریف
[ویرایش]همسایگی اپسیلونی
[ویرایش]
مجموعهٔ باز
[ویرایش]مجموعهای که بتوان حوال آن یک همسایگی ترسیم کرد بهگونهای که اعضای آن همسایگی همگی همچنان عضو مجموعه باشند.
مجموعهٔ فشرده
[ویرایش]مجموعهٔ فشرده (به انگلیسی: Compact set)، در فضای اقلیدسی (در ) مجموعهای است که بسته و کراندار باشد.
تقعر و تحدب توابع
[ویرایش]
تابع مقعر
[ویرایش]تابع مقعر (به انگلیسی: Concave function) تابعی است که اگر دو نقطه روی تابع را به هم وصل کنیم در زیر یا روی نمودار قرار بگیرد.
اگر یک تابع صعودی را بر یک تابع مقعر اعمال کنیم، مقعر بودن به هم میریزد ولی خاصیت شبهتقعر نه (؟)
تابع محدب
[ویرایش]تابع محدب (به انگلیسی: Convex funtion) تابعی است که اگر دو نقطه روی تابع را به هم وصل کنیم در بالا یا روی نمودار قرار بگیرد. نکته: اشتراک دو مجموعه محدب همچنان محدب است اما اجتماع آنها نه (مثلا دو دایره کنار هم)
در مجموعههای محدب اکید، نقاط نمیتوانند روی مرز باشند. (مثلا در یک مربع اضلاع آن همگی روی خود مرز هستند پس محدب است ولی نه اکیدا) به همین علت چون مجموعههای باز نقاط مرزی ندارند، اگر مجموعهٔ بازی محدب باشد محدب اکید است.
تابع شبه مقعر
[ویرایش]
طبق تعریف، مقدار تابع شبه مقعر (به انگلیسی: quasi-concave) در بین دو نقطهٔ و از دو مقدار و پایینتر نمیرود و از این رو تابع دارای حداکثر یک مقدار ماکسیمم و یک قله است. اما تابع شبه مقعر میتواند قسمت پخی (به انگلیسی: flatness) داشته باشد، پس با اینکه جواب یکتاست اما میتواند در چند رخ دهد، حال آنکه در شبه مقعر اکید، خیر.
ضمناً مزیت دیگر تابع شبه مقعر آن است که، شبه تقعر برخلاف تقعر با اعمال یک تابع صعودی به هم نمیریزد.
اثبات میشود که تابعی که مقعر است، شبه مقعر نیز هست.
تفسیر اقتصادی محدببودن ترجیحات یک فرد
[ویرایش]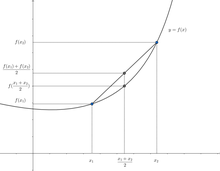
توجه داشته باشید که مطابق یک لم در اقتصاد خرد[۲]، رابطهی ترجیحات (به انگلیسی: Preference Relation) محدب است اگر و تنها اگر تابع مطلوبیت، شبهمقعر باشد. اگر رابطهی ترجیحات محدب باشد، تمامی منحنیهای بیتفاوتی نسبت به مبدا محدب هستند.
تفسیر جمعی بودن مطلوبیت یک فرد
[ویرایش]اگر تابع مطلوبیتی همچون را در نظر بگیریم، خاصیت additive بودن باعث میشود که مطلوبیت نهایی مصرف یک کالا بر مطلوبیت نهایی مصرف کالای دیگر موثر نباشد.
وجود جواب
[ویرایش]در صورت برقراری شروط قضیهٔ مقدار کرانی (به انگلیسی: Extreme Value Theorem) یعنی:
- بستهبودن بازهی تعریف تابع (مثلا قید سوال بهینهسازی یا دامنه) و تهی نبودن این مجموعه
- پیوستهبودن خود تابع در این بازه (یا مجموعه)
تابع اقلا یکبار مقادیر ماکسیمم و مینیمم خود را میگیرد. این دو شرط برای وجود جواب کافی هستند.
برای مطالعه بیشتر به صفحهی همین قضیه در ویکیپدیا مراجعه کنید.
یکتایی جواب
[ویرایش]اگر مجموعهٔ قید، محدب باشد و تابع هدف، شبه مقعر اکید باشد، مسئلهٔ حداکثرساز یا حداقلسازی حداکثر یک جواب دارد. (درمورد وجود جواب اظهار نظر نمیکند)
نکته: از آنجایی که مقعر بودن از شبه مقعر بودن قویتر است، اگر تابع هدف، مقعر اکید هم باشد، جواب یکتا است.
شرط لازم و کافی برای جوابهای مسئلهٔ بهینهسازی
[ویرایش]- شرط لازم کاندیداهای جواب را بررسی و حذف میکند، اگر یک نقطه بخواهد جواب باشد باید شرط لازم را دارا باشد.
- و از بین آنها که پس از حذف با شرط لازم باقی ماند، اگر نقطهای در شرط کافی صدق کند جواب مسئله است.
قضیهٔ تابع ضمنی
[ویرایش]قضیهٔ تابع ضمنی اگرچه به ما تابع صریح را نمیدهد ولی اولاً به ما شروط کافی برای وجود چنین تابعی را، و ثانیاً نحوهٔ محاسبهٔ مشتق این تابع را به ما میدهد. شروط کافی یعنی ممکن است تابعی باشد که فرم صریح داشته باشد اما قضیه نتواند وجود آن را اثبات کند. مثلاً تابع با اینکه فرم صریح دارد () ولی به علت صفر شدن مشتقش در نقاطی که خود تابع صفر میشود (یعنی به ازای همهٔ ها) دیگر تابع اینجا کاربرد ندارد ولی همانطور که دیدیم فرم صریح دارد.
مقعر یا محدب بودن یک تابع
[ویرایش]برای درک هرچه بهتر کاربرد ماتریسها و مباحث بیشتر، میتوانید به بخش ماتریسهای همین کتاب سر بزنید.
ماتریس هشین
[ویرایش]شرط متقارن شدن ماتریس هشین آن است که مشتقات مرتبه دوم تابع همگی پیوسته باشند. یک مثال خوب در اینجا یافت میشود. این آدرس نیز حاوی مثالهای پیشرفتهتر است.
حالت کلی
[ویرایش]برای بررسی تقعر و تحدب یک تابع میتوان از ماتریس هشین استفاده کرد.[۳]
- اگر و مثبت معین باشد، تابع دارای یک مقدار کمینهٔ موضعی اکید در نقطهٔ است.
- اگر و منفی معین باشد، تابع دارای یک مقدار بیشینهٔ موضعی اکید در نقطهٔ است.
- اگر و دارای مقادیر ویژهٔ مثبت و منفی باشد، تابع دارای یک مقدار کمینه یا بیشینهٔ موضعی در نقطهٔ نیست و این یعنی نقطهٔ زینی است.
- اگر به ازای تمامی مقادیر دامنهٔ تابع ، مثبت نیممعین باشد، آنگاه تابع محدب است. این تابع به ازای نقطهای که در آن و مثبت معین باشد، دارای کمینهٔ سراسری اکید است.
- اگر به ازای تمامی مقادیر دامنهٔ تابع ، منفی نیممعین باشد، آنگاه تابع مقعر است. این تابع به ازای نقطهای که در آن و منفی معین باشد، دارای بیشینهٔ سراسری اکید است.
تابع دو متغیره
[ویرایش]نکته مهم: در صورت نبود مشتق دوم تابع مطالب زیر برقرار نیست.
برای توابع دو متغیره، که دو بار مشتق پذیر باشند تابع هشین فوق را داریم: که دترمینان آن هست:
در این حالت:
- دترمینان مثبت است:
- اگر و در حالی که آنگاه بهازای کمینهٔ موضعی دارد.
- اگر و در حالی که آنگاه بهازای بیشینهٔ موضعی دارد.
- اگر به ازای تمامی مقادیر دامنه داشته باشیم: و ، آنگاه محدب است و یک مقدار کمینهٔ اکید سراسری در هر نقطهای که و و دارد.
- اگر به ازای تمامی مقادیر دامنه داشته باشیم: و ، آنگاه مقعر است و یک مقدار بیشینهٔ اکید سراسری در هر نقطهای که و و دارد.
- دترمینان منفی است:
- اگر و ، آنگاه بهازای حالت زینی دارد.
تابع تکمتغیره
[ویرایش]برای یادآوری بررسی تقعر و تحدب توابع تکمتغیره در دامنهی آنها این ویدئو را ببینید.
جستارهای بیرونی
[ویرایش]- جزوهی دانشگاه SFU برای مباحث بسیار مقدماتی بهینهسازی ایستا
- جزوهی دانشگاه SFU برای مباحث اندکی پیشرفتهتر بهینهسازی ایستا
- ویکی-جزوهی دانشگاه Cornell برای بهینهسازی
منابع
[ویرایش]- ↑ Nechyba, Thomas، Microeconomics: An Intuitive Approach with Calculus.
- ↑ http://www.econ.ucla.edu/sboard/teaching/econ11_09/econ11_09_lecture2.pdf
- ↑ https://wj32.org/wp/2013/02/26/convex-functions-second-derivatives-and-hessian-matrices/



![{\displaystyle f[(1-\Theta )x'+\Theta x'']>min\{f(x'),f(x'')\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d98be291d6ff28581dbe92f330f3d927c4db93d)




















