ریاضی پایه/نسخه چاپی
این یک نسخه چاپی است از ریاضی پایه این پیغام و هیچ چیز اضافیای در چاپ نمیافتند اگر میانگیر را خالی کنید. |
نسخه کنونی و قابل ویرایش این کتاب را میتوانید در وبگاه ویکیکتاب در نشانی زیر بیابید
https://fa.wikibooks.org/wiki/%D8%B1%DB%8C%D8%A7%D8%B6%DB%8C_%D9%BE%D8%A7%DB%8C%D9%87
اعداد
اعداد
[ویرایش]این بخش برای دانشآموز یا معلم یا ولی دانش آموز است.
اعداد طبیعی
[ویرایش]وقتی ما سیبها یا پرتقالها یا فیلها را میشماریم از اعداد طبیعی استفاده میکنیم. اعداد طبیعی عبارتند از ۱، ۲، ۳، الخ بدون خاتمه. هیچ بزرگترین عدد طبیعیای وجود ندارد. همیشه یک عدد میتواند با افزودن ۱ به یک عدد طبیعی بزرگتر تبدیل شود.
صفر
[ویرایش]صفر نشاندهنده هیچ است. صفر از هر عدد طبیعی دیگری کوچکتر است. اگر ما صفر سیب یا صفر پرتقال یا صفر فیل داریم به زبان ساده معنیاش این است که هیچ چیز نداریم.
آموزش دادن اعداد
[ویرایش]ارائه تعریفی درست از مفهوم عدد
[ویرایش]معمولا بچهها از سن خیلی کم از طریق توالی واژههای «یک، دو، سه، چهار، پنج، الخ» چیزهایی را در مورد اعداد میآموزند. معمولا این آموزش در ضمن اشاره کردن به یک دسته اسباب بازی یا تعداد پلههای پلکان خانه یا مواردی از این دست انجام میگیرد. در حین گفتن توالی اعداد ممکن است بچه اسباب بازیها یا پلهها را دو بار بشمارد یا نشمارد یا به اشتباه بشمارد. اغلب اوقات از طریق همین فعالیت ها یا فعالیتهای غیررسمی انطباقی است که بچهها با مفهوم اعداد و شمارش آشنا میشوند و در عین حال اشتباهات خود را تصحیح میکنند. نکتهای که وجود دارد این است که بچهها اغلب به حال خود واگذارده میشوند تا با مفاهیم عددی آشنا شوند و ممکن است پایههای لرزانی برای این کار داشته باشند در حالی که میتوان از طریق فعالیتهای مناسب به گونهای عمدی مفاهیم عددی را در بچهها رشد داد. اولین این فعالیتها، انطباق اشیا است.
فعالیتهای انطباقی
[ویرایش]به جای اینکه بچه ها به صورت معمولی با فعالیت های شمارش رو به رو شوند میتوانیم برایشان دستههای انطباقی اشیا فراهم کنیم تا از این طریق پایهای استوار برای مفهوم عدد و ارتباط عددی برای آنها ایجاد کنیم. این نکته بسیار مهم است که فعالیت های انطباقی بایستی فیزیکی باشند تا بچهها بتوانند با آن ارتباط برقرار کنند.
اعداد و شکل نمادین آنها
[ویرایش]آموزگاران معمولا با مقوا یا پلاستیک شکل اعداد را به بچهها نشان میدهند.
ارزش مکانی
[ویرایش]بحث بعدی در آموزش اعداد، ارزش مکانی اعداد است.
همانطور که میدانید عدد پس از ۹ عدد ۱۰ است. در این عدد یک مکان جدید وجود دارد، دهگان. هرگاه عددی که در مکان دوم قرار دارد افزایش یابد، نشاندهنده ۱۰ واحد است. مکان (جایگاه) پس از دهگان، صدگان است و مکان پس از صدگان هزارگان. البته اعداد از این هم میتوانند بزرگتر شوند ولی در اینجا تا همین حد کافی است و فعلا نیازی به اعداد بزرگتر نداریم.
برای درک بهتر موضوع، ۱۰ را میتوانید با یک کیسه حاوی ۱۰ سکه نشان دهیم؛ و ۱۰۰ را با ۱۰ کیسه.
ارزش مکانی در سایر سیستمهای اعداد
[ویرایش]غیر از این سیستم عددیای که معمولا استفاده میکنیم سیستمهای عددی دیگری نیز وجود دارند.
| دودویی | ۰ | ۱ | ۱۰ | ۱۱ | ۱۰۰ | ۱۰۱ | ۱۱۰ | ۱۱۱ |
| دهدهی | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ |
جمع کردن اعداد
جمع کردن دو عدد تک رقمی با هم
[ویرایش]جمع کردن دو عدد تک رقمی بر طبق جدول زیر انجام میشود. کافی است دو عددی را که میخواهید با هم جمع کنید در ستون و ردیف جدول زیر پیدا کنید. محل برخورد ستون و ردیف مربوطه، حاصل جمع دو عدد را به شما نشان میدهد. در کشیدن جدول زیر یک الگوی منظم به کار رفته است؛ با این حال باید از این جدول را از بر باشید چون اولین گام برای ریاضیات ذهنی به شمار میآید.
| + | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ |
|---|---|---|---|---|---|---|---|---|---|---|
| ۰ | ۰ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ |
| ۱ | ۱ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | ۱۰ |
| ۲ | ۲ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | ۱۰ | ۱۱ |
| ۳ | ۳ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | ۱۰ | ۱۱ | ۱۲ |
| ۴ | ۴ | ۵ | ۶ | ۷ | ۸ | ۹ | ۱۰ | ۱۱ | ۱۲ | ۱۳ |
| ۵ | ۵ | ۶ | ۷ | ۸ | ۹ | ۱۰ | ۱۱ | ۱۲ | ۱۳ | ۱۴ |
| ۶ | ۶ | ۷ | ۸ | ۹ | ۱۰ | ۱۱ | ۱۲ | ۱۳ | ۱۴ | ۱۵ |
| ۷ | ۷ | ۸ | ۹ | ۱۰ | ۱۱ | ۱۲ | ۱۳ | ۱۴ | ۱۵ | ۱۶ |
| ۸ | ۸ | ۹ | ۱۰ | ۱۱ | ۱۲ | ۱۳ | ۱۴ | ۱۵ | ۱۶ | ۱۷ |
| ۹ | ۹ | ۱۰ | ۱۱ | ۱۲ | ۱۳ | ۱۴ | ۱۵ | ۱۶ | ۱۷ | ۱۸ |
جمع کردن دو عدد چند رقمی با هم
[ویرایش]ما برای اینکه چند عدد دو رفمی یا سه رقمی را جمع کنیم باید جمع اعداد یک رقمی را کامل بلد باشیم.
برای جمع کردن دو عدد چند رقمی با هم ابتدا از سمت راست به چپ شروع میکنیم. به طور مثال:
۴۳۴۵ ۹۸۷۴+
میگوییم:۹=۴+۵ بنابراین
۴۳۴۵ ۹۸۷۴+۹
میگوییم:۱۱=۴+۷ یعنی ۱ دسته یکی و ۱ دسته دهتایی. دهتایی را در بالای ارزش مکانی بعدی مینویسیم و یکی ای را در نتیجه حاصل جمع بنابراین
۱ ۴۳۴۵ ۹۸۷۴+۱۹
به همین ترتیب
۱۱۱ ۴۳۴۵ ۹۸۷۴+۱۴۲۱۹
آموزش جمع زدن اعداد
[ویرایش]برای آموزش جمع ریاضی به کودکان میتوانید از چیزهای فیزیکی (قابل لمس) استفاده کنید مثلا از چند توپ استفاده کنید. وسایلی که برای آموزش استفاده میکنید باید شبیه به هم باشد تا دانشآموز گیج نشود. یک مثال در اینجا برای شما میآوریم:
من چهار پرتقال در دست دارم و نگین سه پرتقال دارد، دو تا از پرتقالهایم را به نگین میدهم حالا نگین چند پرتقال دارد؟
تفریق کردن اعداد
تفریق کردن اعداد
[ویرایش]تفریق اعداد به این معنی است که وقتی یک تعداد از چیزی داشته باشیم، یک تعداد از آن را برداریم یک تعداد باقی خواهد ماند. به عنوان مثال یک نفر ۷ عدد سیب دارد، ۲ عدد سیب را میخورد؛ پس ۵ = ۲-۷ سیب باقی میماند.
ما مجاز نیستیم یک عدد بزرگتر را از یک عدد کوچکتر کم کنیم زیرا نمی توانیم از یک چیز به تعداد کمتر از صفر داشته باشیم.
عمل تفریق کردن درست عکس جمع کردن است. در زیر، این موضوع به خوبی نشان داده شده است. اگر یک عملیات جمع به صورت ۸ = ۵ + ۳ داشته باشیم، آن را میتوانیم در یک مثلث به صورت زیر نشان دهیم:
۸ \ / ۵ + ۳
الان ضلع چپ و راست مثلث، هر کدام یک تفریق هستند: ۵ = ۳ - ۸ و ۳ = ۵ - ۸ . فرض کنید میخواهید عمل تفریق ۳ - ۸ را انجام دهیم با توجه به ضلع اینکه ۸ و ۳ روی دو ضلع از مثلث قرار دارند و روی ضلع دیگری از مثلث عدد ۵ قرار دارد، جواب ۵ خواهد شد. به عبارت دیگر برای اینکه ۳ به ۸ تبدیل شود باید آن را با ۵ جمع کنید.
تفریق کردن اعداد بزرگ
[ویرایش]برای تفریق کردن اعداد بزرگ رویه زیر پیشنهاد میشود. به دلیل پیچیدگی کار بهتر است از کاغذ و قلم استفاده کنید.
- کار را با آخرین رقم سمت راست شروع کنید.
- عمل تفریق اعداد هر رقم را با عددی که در پایین همان رقم نوشته شده است انجام دهید. این کار برای زمانی است که جواب بزرگتر از صفر شود.
- چنانکه تفریق کردن را از آخرین رقم سمت راست شروع کردهاید همین کار را تا آخرین رقم سمت چپ ادامه دهید.
- اگر جواب کوچکتر از صفر شد و تفریق امکانپذیر نبود، ۱۰ تا به آن رقم بیفزایید و سپس تفریق را انجام دهید.
- از رقم سمت چپ آن، ۱ کم کنید. این کار در صورتی امکانپذیر است که این رقم ۱ یا بیشتر باشد.
- در صورتی که به دلیل صفر بودن امکانپذیر نبود یک ۱ از آن کم کنید بایستی از رقم سمت چپش قرض کنید. بدین صورت که ۱۰ تا به آن رقم بیفزایید و از رقم سمت چپش یک ۱ کم کنید.
برای اینکه بهتر متوجه شوید مثالهای زیر را مرور کنید.
میخواهیم بدانیم جواب ؟ = ۴ - ۲۷ چه میشود.
۲۷ - ۴ --- ؟
بر طبق روندی که توضیح دادیم کار را از آخرین رقم سمت راست شروع میکنیم:
۲۷ - ۴ --- ۳
و سپس رقمهای سمت چپ
۲۷ - ۴ --- ۲۳
ضرب کردن اعداد
آموزش ضرب کردن
[ویرایش]مهارتها و مدلها
[ویرایش]علامت ضرب «×» است.
ضرب کردن دو عدد «۳» و «۵» با هم به این معنی است که عدد ۳ را ۵ بار با خودش جمع کنیم:
۳ + ۳ + ۳ + ۳ + ۳ = ۱۵
عبارت بالا به صورت زیر نشان داده میشود:
۳ × ۵ = ۱۵
در روشهای مدن آموزشی برای آموزش ضرب از الگوریتمهای استاندارد استفاده میکنند مثلن آموزگاری که میخواهد مسئلۀ ۶ × ۴ را آموزش بدهد ۶ کیسه بر میدارد و درون هر کدامشان ۴ مهره میاندازد. در زیر به مدلهایی پرداختهایم که انتزاعیترند اما مدلی که همه دانشآموزان آن را میفهمند و از آن استفاده میکنند مدلی است که مساحت مستطیل نامیده میشود.

مدل مساحت مستطیلی که در شکل بالا نشان داده شده است مربوط به مسئله ۴ × ۹ است که حاصل آن برابر ۳۶ میشود. دقت کنید که عرض مستطیل شامل ۴ واحد و طول مستطیل ما شامل ۹ واحد است. در واقع مستطیل ما از ۴ ردیف و ۹ ستون تشکیل شده است بنابراین دانشآموز میفهمد وقتی ۹ واحد موجود در ردیف اول را ۴ بار تکرار کند حاصل میشود ۳۶.
استفاده از الگوریتمهای مختلف در حل مسئلههای ضرب
[ویرایش]روش شبکهای
[ویرایش]ضرب اعداد اعشاری
[ویرایش]روش ضرب اعداد 19 تا 11 در خودشان
[ویرایش]در اینجا ابتدا رقم های یکان را در هم ضرب می کنیم.برای مثال 12X13 ،ابتدا 2 را ضربدر 3 می کنیم که می شود6.این عدد در یکان قرار می گیرد.سپس یکان ها را باهم جمع کرده و در دهگان قرار می دهیم.مانند:2+3=5.این عدد در رده دهگان قرار می گیرد.سپس دهگان ها را در هم ضرب می کنیم که می شود:1x1=1.این رقم را نیز در صدگان قرار می دهیم. بنابراین،حاصل ضرب 12x13 می شود:156
اگر یکی از این اعداد،یکان یا دهگان اضافه می آورد،باید با رقم قبل از خود جمع شود.برای مثال:19x18. 9x8=72 که ما 2 را یکان قرار می دهیم و عدد 7 را نگه می داریم.9+8=17 .در اینجا،دهگان حاصل،7 است اما چون از قبل یک 7 دیگر داشتیم،با هم دیگر جمع می کنیم:7+7=14 که عدد 4 را دهگان حاصل ضرب قرار می دهیم.حال یک دهگان 14 و یک دهگان 17 داریم که جمع دهگانها می شود 2.حال 1را ضربدر 1 می کنیم و 2تا به آن اضافه می کنیم که صدگان می شود 3.حال،جاصل ضرب اعداد19x18 می شود:342 شما می توانید با تمرین و تلاش،بر این روش مسلط گردید.
تقسیم کردن اعداد
برای آموزش تقسیم کردن به کودکان برای اولین بار بهتر است یک گروه کوچک از آنان را دور هم جمع کنیم، یک چیز را به تعداد مساوی بین آنها تقسیم کنیم. با این کار دانشآموز درک درستی از مفهوم تقسیم پیدا خواهد کرد و سپس وارد فرم نوشتاری تقسیم و تقسیمهای کوتاه و طولانی خواهد شد.
فرآیند تقسیم را باید عکس ضرب دانست، در اینجا نیز به جدول ضرب نیاز است. رابطه بین جمع و تفریق با هم و ضرب و تقسیم با هم وقتی اهمیت پیدا میکند که در مسائل جبری بخواهیم عمل معکوس را انجام دهیم. آموزگاران بایستی توجه داشته باشند به دانشآموزان خود یاد دهند که عمل ضرب درست برعکس تقسیم است و نکتۀ دیگر اینکه تقسیم را از جهت درست انجام دهند.
سادهترین شکل تقسیم به صورت زیر است که برعکس ضرب است:
عبارت بالا به صورت کسری نوشته شده است که نشاندهندۀ تقسیم است؛ علامت دیگری که برای نشان دادن تقسیم استفاده میشود یک خط تیره با یک نقطه بالا و یک نقطه پایین آن است (÷).
عبارت تقسیم بالا تقریبا آسان بود چون فرآیند عکس آن (۱۰ = ۲ × ۵) برای دانشآموز شناختهشده است. مسئله زیر کمی سختتر است:
چون عدد ۹۸ بزرگ است ممکن است دانشآموز نتواند به سوال پاسخ بدهد.
در اینجا باید از تقسیم طولانی استفاده کنیم. ابتدا ۹ (رقم سمت چپ ۹۸) را بر ۲ تقسیم میکنیم. اگر بخواهیم ۹ را بر ۲ تقسیم کنیم جواب عدد صحیح نخواهد شد پس نزدیکترین عدد صحیح را انتخاب میکنیم (۸) که چون در رقم دهگان است پس میشود ۸۰. چون در رقم دهگان به جای ۹ عدد ۸ قرار دادهایم به اندازه ۹−۸ که در ۱۰ ضرب شده باشد به رقم یکان (۸) اضافه میکنیم. پس برای رقم دهگان خواهیم داشت ۸۰ و برای رقم یکان خواهیم داشت ۱۰ + ۸ = ۱۸.
حال رقمهای دهگان و یکان جدید را به طور جداگانه بر ۲ تقسیم کرده و نتایج به دست آمده را با هم جمع میکنیم تا جواب نهایی به دست آید:
۸۰ ÷ ۲ = ۴۰
۱۸ ÷ ۲ = ۹
۴۰ + ۹ = ۴۹
بیایید به بررسی یک مثال دیگر برای تقسیم طولانی بپردازیم. میخواهیم ۱۵۶۹۴۷ را بر ۲ تقسیم کنیم.
حاصل تقسیم ۱۵ بر ۲ یک عدد صحیح نخواهد شد پس به جای ۱۵۰٬۰۰۰ از ۱۴۰٬۰۰۰ استفاده میکنیم و در عوض ۱۰٬۰۰۰ به ۶۹۴۷ اضافه میکنیم میشود ۱۶۹۴۷. به همین ترتیب ادامه میدهیم:
۷۸۴۸۷
۲/۱۵۶۹۴۷
-۱۴۰۰۰۰ (یک یا ۱۵ بر ۲ بخشپذیر نیست اما ۲ × ۷ میشود ۱۴)
۱۶۹۷۴
-۱۶۰۰۰ (دو × ۸ میشود ۱۶)
۹۷۴
-۸۰۰ (نه بر ۲ بخشپذیر نیست اما ۲ × ۴ میشود ۸)
۱۷۴
-۱۶۰ (شانزده به جای ۱۷)
۱۴
-۱۴ (دو × ۷ میشود ۱۴)
۰
عاملها (فاکتورها) و اعداد اول
فاکتورها اعدادی هستند که میتوان آنها را با هم ضرب کرد تا عدد دیگری به دست آورد. به عنوان مثال ۸ و ۱۱ فاکتورهای ۸۸ هستند زیرا ۸۸ =۸ * ۱۱ . به همین ترتیب ۱۰ یک فاکتور برای ۱۰۰ است زیرا ۱۰۰ =۱۰ * ۱۰ .
فاکتورهای اول (عاملهای اول) فاکتورهایی هستند که عدد اول هستند:
۱۱ × ۵ = ۵۵
۵ × ۲ × ۵ × ۲ = ۱۰۰
در اینجا عددهای ۵ و ۲ و ۱۱ به هیچ عددی بخش پذیر نیستند به جز ۱ و خودشان. چنین عددهایی عدد اول نامیده میشوند. اعداد اول یکی از مهمترین بخشها در ریاضیات است، و در علوم رایانه تجزیه عددهای بزرگ به عاملهای اول بحث بسیار مهمی است.
۳۲ × ۲= ۶۴ (عدد اول نیست ۳۲)
یا (۱۶ عدد اول نیست) ۱۶× ۲ × ۲= ۶۴
یا (۸ عدد اول نیست) ۸ × ۲ × ۲ × ۲= ۶۴
یا (۴ عدد اول نیست) ۴ ×۲ ×۲ × ۲ × ۲= ۶۴
یا ۲ × ۲ × ۲ × ۲ × ۲ × ۲= ۶۴
روش فاکتورگیری
در ریاضیات راه رسیدن به جواب، به اندازه خود جواب ارزشمند است. گاهی اوقات راه رسیدن به جواب، یک اثبات است. معمولا مردم وقتی درباره مسائل ریاضی سخن میگویند اسمی از اثبات نمیبرند ولی از نظر من بهتر است عادت کنیم اسم اثبات را بگوییم. روشی که در اینجا میخواهیم شرح دهیم فاکتورگیری به عوامل اول است که اثبات میکند جوابی که به آن رسیدهاید جوابی صحیح است. این کار باعث میشود دچار سردرگمی نشوید، روش کار را به شما نشان میدهد و باعث میشود روش را بهتر درک کنید. خیلی آسان است و افراد مبتدی نیز میتوانند از آن استفاده کنند، با این روش میتوانید چند گام را جلوتر بروید و در زمان صرفهجویی کنید.
pf(۴)
= { ۴ = ۲ × ۲ }
(۲,۲)
در بالا pf را به معنی فاکتورگیری به اعداد اول به کار بردهایم. عدد ۴ را به دو عدد اول ۲ فاکتورگیری کردهایم.
برای اینکه ریاضی را بفهمیم نیاز است که نمادها و زبان ریاضی را یاد بگیریم.
ما از به عنوان نماد فاکتورگیری عدد X به اعداد اول استفاده کردیم. اگر پس از عدد X یک ویرگول (،) قرار بدهیم میتوانیم عددهای اول را که فاکتورگیری به آنها مطلوب ماست درج کنیم. بنابراین (pf(45),2,5) به معنی فاکتورگیری از عدد ۴۵ به دو عدد اول ۲ و ۵ خواهد بود.
اعداد منفی
مقدمه
[ویرایش]این نوشتهها برای دانشآموزان اعم از خردسال و بزرگسال نوشته شده است. اعدا منفی اعدادی هستند که از صفر کوچکترند. یک راه مناسب برای درک مفهوم اعداد منفی این است که آنها را به عنوان اعداد بدهکاری در نظر بگیریم. به عنوان مثال اگر شما منفی چهار عدد سیب داشته باشید به این معنی است که چهار عدد سیب به کسی بدهکار هستید و چهار سیب باید به او بدهید. برای نشان دادن منفی یک خط تیره پشت عدد میگذاریم. در مورد این مثال مینویسیم ۴− سیب.
جمع کردن اعداد منفی
[ویرایش]اگر دو عدد منفی با هم جمع شود، نتیجه یک عدد منفی خواهد شد:
−۴ + −۳ = −۷
میتوانیم منفیها را مثل کاشیهایی تصور کنیم که هر کدام نشاندهنده منفی یک (۱−) هستند (مثلا ۳− را ۳ کاشی در نظر بگیریم):
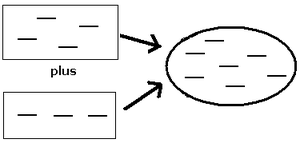
در وضعیتی که بخواهیم یک عدد منفی را با یک عدد مثبت جمع کنیم، شرایط فرق میکند. مثلا میخواهیم مثبت دو (۲+) را با منفی سه (۳−) جمع کنیم. فرض کنید میخواهیم ۲+ را با ۳− جمع کنیم؛ اگر نمادهای مثبت و منفی را بکشیم باید به صورت جفتی آنها را بکشیم یعنی هر علامت مثبت را با یک نماد منفی بکشیم. در اینجا ۲ نماد مثبت و ۳ نماد منفی میکشیم. ۲ نماد مثبت و ۲ نماد منفی که با هم جفت شدهاند را کنار میزنیم و فقط یک نماد منفی باقی میماند. به عبارت دیگر حاصل عبارت ۲+ به علاوۀ ۳− برابر است با ۱−.
ما میتوانیم آن را به صورت زیر بنویسیم:
+۲ + -۳ = -۱
اگر ترتیب را عوض کنیم تغییری رخ نمیدهد:
-۳ + +۲ = -۱
تفریق کردن اعداد منفی
[ویرایش]تفریق کردن اعداد منفی معادل جمع کردن همان اعداد با مقادیر مثبت است. به عبارت دیگر دو نماد منفی یک نماد مثبت را به وجود میآورند.
۵ − −۲ = ۵ + ۲ = ۷
ضرب کردن اعداد منفی
[ویرایش]وقتی دو عدد با هم ضرب میشوند:
- اگر هر دو عدد مثبت باشند حاصل مثبت خواهد شد.
- اگر هر دو عدد منفی باشند حاصل مثبت خواهد شد.
- اگر یک عدد، مثبت و عدد دیگر، منفی باشد حاصل منفی خواهد شد.
بنابراین:
۵ × ۲ = ۱۰
−۵ × −۲ = ۱۰
۵ × −۲ = −۱۰
−۵ × ۲ = −۱۰
در ضرب میتوانیم جای عددها را جابجا کنیم و در پاسخ تغییری به وجود نمیآید:
۲ × ۵ = ۱۰
−۲ × −۵ = ۱۰
۲ × −۵ = −۱۰
−۲ × ۵ = −۱۰
تقسیم کردن اعداد منفی
[ویرایش]برای تقسیم کردن ابتدا بدون در نظر گرفتن علامت منفی یا مثبت عددها، تقسیم را انجام دهید و سپس بر اساس قاعده زیر علامت عدد پاسخ را تعیین کنید.
در عمل تقسیم:
- اگر هر دو عدد مثبت باشند حاصل مثبت خواهد شد.
- اگر هر دو عدد منفی باشند حاصل مثبت خواهد شد.
- اگر یک عدد، مثبت و عدد دیگر، منفی باشد حاصل منفی خواهد شد.
۱۰ ÷ ۲ = ۵
−۱۰ ÷ −۲ = ۵
۱۰ ÷ −۲ = −۵
−۱۰ ÷ ۲ = −۵
در تقسیم نمیتوانیم جای عددها را جابجا کنیم.
نکته
[ویرایش]گاهی عددهای منفی را درون پرانتز یا با رنگ قرمز نشان میدهند.
کسرها
یاد گرفتن کسرها
[ویرایش]کسرها یا اعداد نسبی (نسبتها) در واقع همان تقسیم هستند؛ از کسرها معمولا برای بیان اعداد کوچکتر از یک (مثل نیم، یک چهارم) استفاده میشود. کسرها یک صورت (در بالای خط کسری) و یک مخرج (در پایین خط کسری) دارند. اگر صورت کسر بزرگتر از مخرج آن باشد، آن کسر بزرگتر از یک است.
روشهای جدید برای آموزش کسر
[ویرایش]روشهایی که امروزه برای آموزش دادن ریاضی و کسر به کار میرود با روشهای ده سال پیش کلا متفاوت است. تفاوتشان در این است که در روش جدید سعی میشود درک تصویری برای راههای خاص کار کردن با کسرها ایجاد شود اما در روش قدیمی از همان ابتدای آموزش فقط از متغیرها استفاده میشد. استفاده از کاشیهای رنگی مرتب شده میتواند برای آموزش کسرها مفید باشد.
اریگامی و کسرها
[ویرایش]اریگامی به مدلهای مربعی و دایرهای
[ویرایش]- یک مربع که به چند کسر تقسیم شده است
- یک دایره که به چند کسر تقسیم شده است
روش پول
[ویرایش]به روش پول با کمک سوالهای زیر میتوانید کسرها را آموزش دهید:
- یک تومان چند ریال است؟
کسرهای عدد کامل
[ویرایش]مثلا یک کسر عدد کامل است.
ضرب کردن کسرها
[ویرایش]
روش سنتی ضرب
[ویرایش]
انجام عملیات روی کسرها
انجام عملیات روی کسرها
[ویرایش]اعداد مخلوط و کسرهای دارای صورت بزرگ:
عدد مخلوط به عددی گفته میشود که از یک عدد صحیح و یک جزء کسری تشکیل شده باشد مثل چهار و نیم؛ کسر دارای صورت بزرگتر کسری است که صورتش بزرگتر از مخرجش باشد مثل ۳/۷. برای ضرب و تقسیم نبایستی از اعداد مخلوط استفاده کنید. از چینن اعدادی فقط برای جمع و تفریق استفاده کنید. برای این کار ابتدا اعداد صحیح و سپس کسرها را با هم جمع یا تفریق کنید.
ضرب:
تقسیم: برای تقسیم باید عدد اول را در معکوس عدد دوم ضرب کنیم.
یعنی مخرج رابه جای صورت و صورت رابه جای مخرج می نویسیم و بعد ضرب می کنیم
اعداد اعشاری
اعشار روشی است برای نمایش دادن اعداد جزئی بدون اینکه از کسر استفاده کنیم. کاربرد این اعداد را در شمارش پول و در جاهای دیگر میتوانید ببینید. برای نوشتن اعداد اعشاری از ممیز استفاده میکنیم و نماد آن ٫ است مثلا ۴۸٫۱۱. مخرج اعداد اعشاری را میتوان به صورت نمایی نوشت. به عنوان مثال برای ۰٫۵۶ یا ۵۶/۱۰۰ مخرج کسر عبارت است از ۱۰^۲.
جمع و تفریق کردن اعداد اعشاری
[ویرایش]هنگام جمع یا تفریق اعداد را بایستی به گونهای زیر هم بنویسید که ممیزها زیر هم قرار بگیرند. اگر همتای یک رقم اعشاری خالی بود آن را صفر در نظر بگیرید.
۱۶٫۳۷ + ۲٫۵ ------ ۱۸٫۸۷
ضرب کردن
[ویرایش]برای ضرب کردن ممیزها را بردارید و مثل دو عدد معمولی دو عبارت را در هم ضرب کنید در آخر به تعداد رقمهای بعد از ممیز هر دو عدد، اعشار بزنید.
- ۴٫۵۲۲
- ×۱٫۲
- ----------
- ۵٫۴۲۶۴
تقسیم کردن
[ویرایش]تقسیماعداد اعشاری دو نوع است: نوع اول و نوع دوم. نوع اول یعنی فقط مقسوم اعشاری باشد و نوع دوم یعنی علاوه بر مقسوم، مقسوم علیه هم اعشاری باشد.
- روش نوع اول: یک خط راست از ممیز میکشیم و قسمت صحیح و اعشاری جدا میشود و قسمت صحیح را مانند تقسیم عادی حل میکنیم وقتی به ممیز رسیدیم یک ممیز در خارج قسمت قرار میدهیم و سپس بقیه بقیه را ساده برهم تقسیم میکنیم.
- روش نوع دوم: باید مقسوم و مقسوم علیه رابر 1000,100,10یا... ضرب کنیم تا اعشار مقسوم علیه ازبین برود. اگر مقسوم علیه یک رقم اعشار داشت در ۱۰، اگر دو رقم اعشار داشت در ۱۰۰ و ... ضرب میکنیم و بقیه مراحل را مانند نوع اول انجام میدهیم
تبدیل کسرها به اعداد اعشاری
[ویرایش]اگر کسر مخرج توانی از ۱۰(۱۰،۱۰۰،۱۰۰۰و...) باشد صورت را می نویسیم و به اندازهی صفر های مخرج اعشار میزنیم.
اگر مخرج توانی از ۱۰ نبود،صورت و مخرج را در عددی ضرب می کنیم که مخرج به توانی از ۱۰ برسد.سپس صورت جدید به دست آمده را گذاشته و به اندازه ی صفر های مخرج اعشار میزنیم
تبدیل اعداد اعشاری به کسر
[ویرایش]اعداد اعشاری را که دور گردش نداشته باشند (بعد از ممیز تعداد رقمها نامحدود نباشد) میتوان به کسر تبدیل کرد. در صورت کسر یک عدد بدون اعشار قرار میگیرد و در مخرج کسر عدد یک با چند صفر در جلوی آن قرار میگیرد.
اعداد اعشاری نامحدود را نیز میتوان به حالت کسری نوشت ولی نیاز دارد که با جبر آشنایی داشته باشید.
ارقام معنیدار
[ویرایش]اعداد اعشاریای که از اندازهگیریها به دست میآورید ممکن است خیلی دقیق نباشند به همین دلیل تعداد رقمهای معنیدار بعد از ممیز را با توجه به دقتی که نیاز دارید انتخاب میکنید.
درصد
مقدمه
[ویرایش]درصد مقداری است که بر ۱۰۰ تقسیم شده باشد، و برای نشان دادن آن از نماد درصد (٪) استفاده میشود. برای مثال ۴٪ برابر است با مقدار اعشاری ۰٫۰۴ یا همان کسر .
کاربردهای درصد
[ویرایش]از زمانهای گذشته درصد برای بیان تغییرات به خصوص در زمینه پول به کار گرفته شده است. به عنوان مثال یک مغازه ممکن است اجناس خود را با ۲۰٪ تخفیف به فروش برساند یا یک بانک وام با بهره ۲۰٪ به مشتریان خود بدهد.
تعیین مبنا
[ویرایش]مبنای درصد مقداری است که از آن شروع میکنیم. بسیاری از اشتباهات در محاسبه درصد به تعیین مبنا مربوط میشود.
مثال
[ویرایش]در یک مغازه قیمت کالایی ۱۰۰$ است، بر روی آن برچسب تخفیف ۲۰٪ خورده است؛ اگر ۶٪ به عنوان مالیات فروش بپردازید قیمت نهایی آن چقدر خواهد بود؟
- ابتدا محاسبه میکنیم ۲۰٪ از ۱۰۰$ چقدر میشود، سپس ۶٪ آن را به عنوان مالیات در نظر گرفته و آن را به قیمت کالا میافزاییم تا قیمت نهایی محاسبه شود.
اصطلاحاتی که همراه درصد به کار میروند
[ویرایش]- اگر شما کالایی را با ۲۰٪ تخفیف بخرید، به این معنا است که قیمت جدید آن برای شما ۲۰٪ کمتر از قیمت اصلی (۱۰۰٪) آن بوده است. به عبارت دیگر ۸۰٪ قیمت اصلی را برای خرید آن کالا پرداخت کردهاید.
- اگر از یک مبلغ، ۲۰٪ سود به شما تعلق بگیرد، به این معنا است که ۲۰٪ بیشتر از قیمت اصلی (۱۰۰٪) آن یا ۱۲۰٪ قیمت اصلی را دریافت کردهاید. (توجه داشته باشید که این فقط سود ساده بوده و یک مفهوم دیگر به نام سود ترکیبی داریم که در زیر به آن میپردازیم)
سود ترکیبی
[ویرایش]سود ساده وقتی است که فقط یک بار درصد سود را به مقدار مبنا بیفزاییم.
سود ترکیبی وقتی است که چند بار درصد سود را به مقدار موجود بیفزاییم.
به عنوان مثال فرض کنید ۱۰۰۰$در بانک پسانداز کردهام و نرخ سود سالیانه بانک ۱۰٪ است که این سود به مدت ۳ سال به صورت ترکیبی به پسانداز من تعلق میگیرد. پس از سال اول ۱۰۰$ سود به من داده خواهد شد و موجودی من در بانک به ۱۱۰۰$ خواهد رسید. در پایان سال دوم نه تنها به ۱۰۰۰$ اولیه پسانداز سود تعلق میگیرد بلکه به ۱۰۰$ سود داده شده نیز سود تعلق میگیرد. به این ویژگی ترکیبی، سود تعلق گرفته به سود میگویند.
فرمول کلی محاسبه سود ترکبی به صورت زیر است:
T = P x (1 + I)N
که در این فرمول:
T = موجودی نهایی P = اصل سرمایه I = نرخ سود دوره ترکیبی N = تعداد دورههای ترکیبی
سیستم متریک
سیستم متریک که ریشه آن به فرانسه سال ۱۷۹۱ بر میگردد سیستم استاندارد کنونیای است که برای اندازهگیریها استفاده میشود. سه یکا هستند که به فراوانی در سیستم متریک مورد استفاده قرار میگیرند:
☞ متر (m): یکای اندازهگیری طول
☞ گرم (g): یکای اندازهگیری جرم
☞ ثانیه (s): یکای اندازهگیری زمان
با انجام اعمال ضرب و تقسیم میتوانیم یکاهای بالا را به یکاهای بزرگتر یا کوچکتر از خودشان تبدیل کنیم.
متر
[ویرایش]متر یکای استاندارد طول است. هر متر به طور تقریبی برابر است با ۳۹٫۳۷ اینچ (۳٫۲۷ فوت) در سیستم رایج آمریکایی.
هر هزار متر برابر است با یک کیلومتر (km).
گرم
[ویرایش]گرم، یکای اندازهگیری جرم است. معمولا برای بیان وزن اجسام نیز از این یکا استفاده میکنند (هر چند صحیح نیست).
هر هزار گرم معادل یک کیلوگرم (kg) است.
هر هزار کیلوگرم معادل یک تن (t) است.
لیتر
[ویرایش]لیتر (L) یکای اندازهگیری حجم مایعات است. یک لیتر برابر است با یک مکعب آب به ابعاد ۱۰سانتیمتر * ۱۰سانتیمتر * ۱۰سانتیمتر. یک میلیلیتر (mL) برابر یک سانتیمتر مکعب است.
عبارتهای زمان
ریاضی زمان
[ویرایش]انجام عملیات ریاضی به دلیل اینکه از یکاهای گوناگونی استفاده میشود مشکل است.
یکاها
[ویرایش]ثانیه
[ویرایش]ثانیه، یکای پایه برای اندازهگیری زمان است. در موضوعات علمی حتی برای اندازهگیری زمانهای بزرگ نیز از این یکا استفاده میشود البته به همراه استفاده از علایم علمی (مثل نما). معمولا ثانیه را به صورت «s» یا «sec» مخفف نشان میدهند.
دقیقه
[ویرایش]هر دقیقه برابر با ۶۰ ثانیه است. مخفف دقیقه به صورت «m» یا «min» نشان داده میشود.
ساعت
[ویرایش]هر ساعت برابر ۶۰ دقیقه یا ۳۶۰۰ ثانیه است. مخفف ساعت به صورت «h» یا «hr» نشان داده میشود.
روز
[ویرایش]هر روز شامل ۲۴ ساعت است. بنابراین هر روز ۱۴۴۰ دقیقه است. مخفف روز به صورت «d» نشان داده میشود.
هفته
[ویرایش]هر هفته ۷ روز دارد. با این حساب هر هفته ۷ × ۲۴ یا به عبارتی ۱۶۸ ساعت دارد. مخفف هفته به صورت «w» نشان داده میشود.
ماه
[ویرایش]هر ماه ۱/۳ ۴ هفته دارد. در واقع هر ماه چیزی بین ۲۸ تا ۳۱ روز دارد. مخفف ماه به صورت «m» نشان داده میشود.
سال
[ویرایش]هر سال چیزی حدود ۳۶۵ روز دارد. سالها به طور عادی ۳۶۵ روزی هستند اما اگر کبیسه باشد، ۳۶۶ روزی است.سال کبیسه معمولا هر ۴ سال یک بار اتفاق میافتد. هر سال، ۱۲ ماه دارد. مخفف سال به صورت «y» یا «yr» نشان داده میشود.
زمانهای طولانیتر از سال به شرح زیر است:
- دهه = ۱۰ سال
- سده = ۱۰۰ سال
- هزاره = ۱۰۰۰ سال
سیستمها
[ویرایش]سیستم ۱۲ ساعته (زمان)
[ویرایش]در این سیستم ۱۲ ساعت اول را «قبل از ظهر» و ۱۲ ساعت دوم را «بعد از ظهر» مینامند که به ترتیب به صورت AM و PM نشان داده میشود. چیز عجیب در این سیستم این است که هیچ وقت ساعت صفر نمیشود بلکه به جای آن ساعت کامل یعنی ۱۲ است.
سیستم ۲۴ ساعته (زمان)
[ویرایش]در این سیستم که گاهی به آن سیستم نامی نیز میگویند اولین عدد، صفر است و تا بیست و چهار ساعت کامل شمارش انجام میگیرد.
سیستم اعشاری (زمان)
[ویرایش]در زمان انقلاب فرانسه تلاش در جهت رواج سیستمی صورت گرفت که در آن هر روز به ۱۰ ساعت و هر ساعت به ۱۰۰ دقیقه تقسیم میشد.
عملیات چهارگانه
[ویرایش]جمع کردن دو بازه زمانی با هم مثل جمع عادی است مگر اینکه بخواهید یکاها را تغییر دهید.
ثانیه ۳۶ = ۵ ثانیه + ثانیه ۳۱
میتوانیم بازه زمانی را در یک عدد اسکالر (بدون یکا) ضرب کنیم.
ثانیه ۱۰ = ۵ ثانیه × ۲
عبارتهای یکا
ریاضی یکا
[ویرایش]تا بدین جا تمام اعدادی که استفاده کردیم اسکالر (بدون واحد) بودند؛ اما در جهان واقعی بیشتر اعداد یکاهای مربوط به خود را دارند. قوانین ویژهای وجود دارد که هنگام انجام عملیات ریاضی بر روی اعداد دارای یکا قابل استفاده هستند.
جمع و تفریق
[ویرایش]قوانین زیر بایستی پیاده شوند:
- اگر یکاها یکسان هستند، به صورت عادی جمع و تفریق کنید.
- اگر یکاها متفاوت هستند دو حالت وجود دارد:
- اگر بتوان آنها را به یکاهای یکسان تبدیل کرد، جمع یا تفریق را باید انجام داد.
- اگر نمیتوان آنها را به یکاهای یکسان تبدیل کرد، جمع یا تفریق قابل انجام نیست.
نمونهها
[ویرایش]ب۷ سیب = + ۳ سیب + ۴ سیب
ب۱ سیب = + ۳ سیب - ۴ سیب
ب؟ = ۳ پرتقال + ۴ سیب
این دو با هم قابل جمع نیستند اما به طور غیرمستقیم روشهایی برای جمع بستن وجود دارد مثلا میتوانیم آنها را به «تکه میوه» تبدیل کرده و با هم جمع کنیم. نتیجه به صورت زیر خواهد شد:
ب۷ تکه میوه = ۳ تکه میوه + ۴ تکه میوه
در بیشتر مواقع در راه حل از روش تبدیل به یکاهای استاندارد استفاده میشود (مثلا ۱ فوت = ۱۲ اینچ):
ب۱۵ اینچ = ۳ اینچ + ۱۲ اینچ = ۳ اینچ + ۱ فوت
ضرب و تقسیم
[ویرایش]هنگام ضرب یا تقسیم اعداد دارای یکا، یکاها نیز همراه اعداد ضرب یا تقسیم میشوند.
نمونهها
[ویرایش]۲ فوت × ۳ فوت = ۶ فوت۲ = ۶ فوت مربع
۶ فوت مربع / ۲ فوت = ۳ فوت
۲ متر × ۳ متر × ۴ متر = ۲۴ متر مکعب = ۲۴ م۳
۲۴ م۳ / ۲ متر = ۱۲ م۲
توان، ریشه و نما
[ویرایش]مثل ضرب و تقسیم، هر عملیاتی که بر روی اعداد انجام میشود بر روی یکاها نیز اعمال میشود.
نمونهها
[ویرایش](2 ft)³ = 2³ ft³ = 8 ft³ = 8 cubic ft
تبدیل یکا
[ویرایش]گاهی نیاز میشود که یکاها را به هم تبدیل کنیم. همانطور که دیدیم این کار از طریق حذف با یکدیگر قابل انجام است.
نمونهها
[ویرایش]۱۰ مایل در روز را به اینچ در ثانیه تبدیل میکنیم (یکاهای یکسان با هم خط میخورند):
۱۰ مایل/روز ×
۵۲۸۰ فوت/مایل
= ۵۲۸۰۰ فوت/روز
۱۲ اینچ/فوت ×
۵۲۸۰۰ فوت/روز
= ۶۳۳۸۰۰ اینچ/روز
۶۳۳۸۰۰ اینچ/روز ×
۱ روز/۲۴ ساعت
= ۲۶۴۰۰ اینچ/ساعت
۲۶۴۰۰ اینچ/ساعت ×
۱ ساعت/۲۴ دقیقه
= ۴۴۰ اینچ/دقیقه
۴۴۰ اینچ/دقیقه × ۱ دقیقه/۶۰ ثانیه = ۷٫۳۳۳۳۳ اینچ/ثانیه
معرفی رقمهای معنیدار
رقمهای معنیدار یک روش است برای اینکه یک دامنه از مقادیر را نشان دهیم. رقمهای معنیدار در جایی به کار میرود که یک کمیت مقدارش از آنچه تعیین شده است متفاوت باشد و بدین ترتیب برای اعداد اندازهگیری شده یا تخمینزده شده به کار میروند.
مثالها
[ویرایش]در حالت عادی رقمهای معنیدار به صورت زیر است:
برای ۲۰۰۰
۲۰۰۰ ±۵۰۰ = ۱۵۰۰ تا ۲۵۰۰
۲۰۰ برای
±۵۰ ۲۰۰ = ۱۵۰ تا ۲۵۰
۲۰ برای
±۵ ۲۰ = ۱۵ تا ۲۵
۲ برای
۲ ± ۰٫۵ = ۱٫۵ تا ۲۰٫۵
محدودیتها
[ویرایش]- رقمهای معنیدار که میتوان به عدد پایه افزود با رقمهای معنیداری که میتوان از عدد پایه کم کرد برابر هستند.
- مقداری که میافزاییم یا کم میکنیم بایستی ۵ برابر شده باشد یا اینکه بر فاکتور ۱۰ تقسیم شده باشد.
- برای یک مقدار دقیق، هیچ خطا یا تغییری لحاظ نمیکنیم. برای مثال $8472.35 فقط به معنی $8472.35 است.
استفاده از رقمهای معنیدار برای بیان علمی یا مهندسی
[ویرایش]برای اعداد بزرگی مثل ۲۰۰۰ ± ۵۰ استفاده از بیان علمی ضروری است. نکتهای که در بیان علمی بایستی توجه داشت این است که پشت ممیز صفر قرار نمیگیرد مثلا ۰٫۲۰ × ۱۰۴ اشتباه است و به جای آن باید بنویسیم:
۲٫۰ × ۱۰۳
توان، ریشه و نما
نما
[ویرایش]توان یا نما یک راه برای نشان دادن این است که یک عدد باید چند بار در خودش ضرب شود. در عبارت ۲۵ عدد ۲ پایه و عدد ۵ نما یا توان نامیده میشود.
چند نکته درباره توان
[ویرایش]- نکته اول هر عددی به توان یک میشود خودش.
- نکته دوم هر عددی به توان صفر میشود یک.
- نکته سوم یک به توان هر عددی میشود یک.
- نکته چهارم هرگاه یک عدد منفی به توان یک عدد زوج برسد حاصل مثبت است اما اگر به توان یک عدد فرد برسد حاصل منفی است.
بیان علمی و مهندسی
در بیان علمی و مهندسی هدف این است که اعدادی را که خیلی بزرگ یا کوچک هستند به گونهای ساده نشان دهیم. در بیان سنتی این کار مشکل است و نمیتوان اعدادی مثل عدد زیر را به سادگی بیان کرد:
123,456,000,000,000,000,000,000,000
یکی از راهها برای نشان دادن چنین اعدادی استفاده از توان است:
123,456 × 1021
عدد زیر را داریم
0.000 000 000 000 000 000 000 000 000 000 378
میتوانیم آن را به یکی از شکلهای زیر نمایش دهیم:
378 × 10-30 37.8 × 10-31 3.78 × 10-32 0.378 × 10-33
میانگین، میانه و نما
میانگین، میانه و نما
[ویرایش]از میان شاخصهای گرایش به مرکز سه تا از همه مهمتر هستند و چند شاخص دیگر هم هستند که کمتر استفاده میشوند، این شاخصها به ما میگویند در یک مجموعه داده چه مقداری مشخصکننده است. برای شاخصهای مرکزی معمولا نیاز است که دادهها را از کوچک به بزرگ مرتب کنیم.
نما
[ویرایش]در یک تعریف ساده، نما به دادهای گفته میشود که در یک مجموعه از اعداد بیشتر از همه رخ دهد. برای مثال اگر در یک کلاس هفت نفر ۱۲ ساله باشند، ده نفر ۱۳ ساله باشند و چهار نفر ۱۴ ساله نما ۱۳ است زیرا بیش از هر سن دیگری ۱۳ ساله وجود دارد. در انتخابات به نما معمولا «حداکثر آرا» گفته میشود و نامزدی که بیشترین آرا را کسب کند برنده انتخابات است حتی اگر تعداد آرای او حداکثر (بیشتر از نصف) کل آرا نباشد.
میانه
[ویرایش]میانه در وسط چند مقدار در یک مجموعه از مقدارها قرار دارد. برای مثال اگر سه دانشآموز در یک آزمون نمرههای ۸۱، ۸۴ و ۹۳ گرفته باشند، مقدار وسط که ۸۴ است به عنوان میانه انتخاب میکنیم.
میانگین
[ویرایش]میانگین معمولی یا میانگین حسابی (که گاهی اوقات متوسط نیز نامیده میشود) برابر است با حاصلجمع تمام مقدارها تقسیم بر تعداد مقدارها. برای مثال اگر سه دانشآموز در یک آزمون نمرههای ۸۱، ۸۴ و ۹۳ گرفته باشند، میانگین برابر است با
۸۱ + ۸۴ + ۹۳ / ۳
که میشود ۸۶.
انواع میانگین
[ویرایش]میانگین وزنی
[ویرایش]میانگین وزنی یا میانگین وزندار شبیه به میانگین معمولی است منتها یک فرق دارد. وقتی مقادیر را با هم جمع میکنیم هر کدام یک عامل وزنی دارند و جمع کل مقدارها را باید بر جمع کل عاملهای وزن تقسیم کنیم. با وجود این عاملهای وزندار میتوانیم بگوییم بعضی از مقدارهای ما در نهایت «مهمتر» از بقیه هستند.
- مثال
دو کلاس داریم که یکی از کلاسها ۲۰ دانشآموز و کلاس دیگر ۳۰ دانشآموز دارد. در یک آزمون نمرههای دانشآموزان این دو کلاس به شرح زیر است (از ۱۰۰ نمره):
- کلاس صبح = ۶۲، ۶۷، ۷۱، ۷۴، ۷۶، ۷۷، ۷۸، ۷۹، ۷۹، ۸۰، ۸۰، ۸۱، ۸۱، ۸۲، ۸۳، ۸۴، ۸۶، ۸۹، ۹۳، ۹۸
- کلاس بعد از ظهر = ۸۱، ۸۲، ۸۳، ۸۴، ۸۵، ۸۶، ۸۷، ۸۷، ۸۸، ۸۸، ۸۹، ۸۹، ۸۹، ۹۰، ۹۰، ۹۰، ۹۰، ۹۱، ۹۱، ۹۱، ۹۲، ۹۲، ۹۳، ۹۳، ۹۴، ۹۵، ۹۶، ۹۷، ۹۸، ۹۹
میانگین هندسی
[ویرایش]در میانگین هندسی به دنبال عددی هستیم که پس از ضرب کردن بین عددها قرار میگیرد نه جمع کردن و تفریق کردن. به عنوان مثال میانگین هندسی ۱۲ و ۳ میشود ۶. فرمول ریاضی برای محاسبه میانگین هندسی دو عدد به صورت زیر است:
که در آن A عدد اول و B عدد دوم هستند.
بنابراین میانگین هندسی ۱۲ و ۳ به صورت زیر محاسبه میشود:
احتمالات
احتمال
[ویرایش]در ریاضیات احتمال به ما میگوید چقدر احتمال دارد یک چیزی اتفاق بیفتد.
اگر چیزی قطعاً اتفاق میافتد میگوییم احتمال آن یک است. به صورت درصد یا کسری نیز میتوانیم احتمال یک چیز را نشان دهیم مثلاً وقتی میگوییم احتمال یک چیز ۲۵٪ است یعنی احتمال تقریباً کمی دارد.
احتمال را به صورت تابع P(X) = y نشان میدهیم. X نشانده حالت مورد انتظار است، به جای X عدد قرار نمیدهیم. y مقدار احتمال است.
به عنوان مثال:
P (برنده شدن پرسپولیس) =
۰٫۶









