ویکی‌جزوه/دانشکده:فنی و مهندسی/انتقال حرارت/تبادل تشعشع بین سطوح

می‌دانیم که انتقال گرمای رسانشی و جابه‌جایی نیازمند گرادیان دما در ماده است ولی انتقال گرما توسط تشعشع به ماده نیاز ندارد. تشعشع فرآیند بسیار مهمی است و از نظر فیزیکی شاید جالب‌ترین نوع انتقال گرما است. بسیاری از فرآیندهای گرمایش، سرمایش، خشک کردن صنعتی و همچنین روش‌های تبدیل انرژی نظیر احتراق سوخت فسیلی وتشعشع خورشیدی با فرآیند تشعشع سروکار دارند.

جسمی را در نظر بگیرید که ابتدا در دمای $Ts$ که از دمای $Tsur$ اطراف بیشتر است قرار دارد و پیرامون آن خلا است . وجود خلا مانع دفع انرژی رسانشی یا جابه‌جایی است ولی می‌دانیم که جسم سرد می شود و سرانجام با اطراف به تعادل گرمایی می‌رسد. این سرمایش با کاهش انرژی داخلی ذخیره شده در جسم همراه است و بر اثر گسیل تشعشع گرمایی از سطح روی می‌دهد. سطح نیز تشعشع گسیل شده از اطراف را جذب می کند. اگر ، آهنگ خالص انتقال گرمای تشعشعی $qrad$ از سطح است و سطح سرد می شود تا $Ts$ به $Tsur$ برابر گردد.

تشعشع گرمایی را آهنگ گسیل انرژی از ماده بر اثر دمای آن می دانیم . در همین لحظه ، تمامی اجسامی که در اطراف شما قرار دارند تشعشع گرمایی گسیل می کنند : مبلمان و دیوارهای اتاق در صورتی که در داخل باشید ، یا زمین ، ساختمان ، اتمسفر و خورشید اگر در بیرون هستید. مکانیزم گسیل به انرژی آزاد شده ناشی از نوسان ها یا انتقال الکترونهای بسیاری که ماده را تشکیل می دهند مربوط می شود. این نوسانها ناشی از دمای ماده هستند، از این رو، تشعشع گرمایی را به شرایط برانگسخته گرما یی داخل ماده مربوط می دانیم.

تمام شکلهای ماده تشعشع می کنند . در گازها و اجسام نیمه شفاف ، مانند شیشه و بلورهای نمکدر دماهای زیاد ، گسیل تشعشع یک پدیده حجمی است . ضریب دید برای محاسبه تبادل تشعشع بین دو سطح ، ابتدا ضریب دید را ( که به آن ضریب وضعیت یا ضریب شکل نیز گویند ) تعریف می کنیم. ضریب دید کسری از تشعشع خروجی از سطح $j$ است که توسط سطح $i$ دریافت می شود. برای تعیین عبارت کلی $Fij$ ، سطوح $Ai$ و $Aj$ را که وضعیت آنها به طور اختیاری است در نظر میگیریم. مساحتهای جزیی هر سطح ،$dAi$ و $dAj$ ، با خطی به طول R به هم وصل شده اند. این خط با عمودهای $ni$ و $nj$ وارده بر سطوح ، به ترتیب ، زوایای قطبی و را می سازد . مقادیر R ، teta1 و teta2 با تغییر مکان جزء مساحت روی $Ai$ و $Aj$ تغییر می کنند . از تعریف شدت تشعشع ، معادله آهنگ تشعشعی را که از $dAi$ خارج و توسط $dAj$ دریافت می شود به صورت زیر می توان بیان کرد:

${\begin{aligned}&{{Q}_{d{{A}_{1}}}}_{\to d{{A}_{2}}}={{I}_{1}}\cos {{\theta }_{1}}d{{A}_{1}}d{{w}_{12}}\\&d{{w}_{12}}={\frac {ds}{{r}^{2}}}={\frac {d{{A}_{2}}\cos {{\theta }_{2}}}{{r}^{2}}}\\&{{Q}_{d{{A}_{1}}}}=\int \limits _{semi-sphere}{{{Q}_{d{{A}_{1}}\to d{{A}_{2}}}}=\pi {{I}_{1}}d{{A}_{1}}}{\text{ }}\\&{{Q}_{d{{A}_{1}}}}=\int {{{Q}_{d{{A}_{1}}}}=\pi {{I}_{1}}{{A}_{1}}}\\&{{Q}_{{{A}_{1}}\to {{A}_{2}}}}=\iint \limits _{{{A}_{1}}{{A}_{2}}}{\frac {{{I}_{1}}\cos {{\theta }_{1}}\cos {{\theta }_{2}}d{{A}_{1}}d{{A}_{2}}}{{r}_{12}}}\\&{{F}_{1-2}}={\frac {{Q}_{{{A}_{1}}\to {{A}_{2}}}}{{Q}_{{A}_{1}}}}={\frac {1}{{A}_{1}}}\iint \limits _{{{A}_{1}}{{A}_{2}}}{{\frac {\cos {{\theta }_{1}}\cos {{\theta }_{2}}}{\pi {{r}_{12}}}}d{{A}_{1}}d{{A}_{2}}}\\&{{F}_{2\to 1}}={\frac {1}{{A}_{2}}}\iint \limits _{{{A}_{1}}{{A}_{2}}}{\frac {\cos {{\theta }_{1}}\cos {{\theta }_{2}}d{{A}_{1}}d{{A}_{2}}}{\pi {{r}_{12}}}}\\&\\&\\&\\\end{aligned}}$

با برابر قرار دادن انتگرال‌ها رابطه مهم تقابل بدست می‌آید. در واقع برای تعیین یک ضریب دید از روی ضریب دید دیگر می توان از رابطه تقابل استفاده نمود. این رابطه به صورت زیر می‌باشد:

$A_{i}F_{ij}=A_{j}F_{ji}$

همچنین قانون جمع‌زنی زیر را برای هر یک از $N$ سطح داخل یک محفظه می توان بکار برد:

$\sum \limits _{j=1}^{N}{F_{ij}=1}$

مثال1)

_________________________________________________________________________________________________________________

مطابق جدول 2-13 کتاب ضریب دید برای دیسکهای موازی هم محور مطابق فرمول داده شده است.

${\begin{aligned}&{{R}_{1}}={\frac {{r}_{1}}{L}}\\&{{\text{R}}_{2}}={\frac {{r}_{2}}{L}}\\&S=1+{\frac {1+{{R}_{2}}^{2}}{{{R}_{1}}^{2}}}\\&{{F}_{1\to 2}}={\frac {1}{2}}\left\{S-{{\left[{{S}^{2}}-4{{\left({\frac {{r}_{2}}{{r}_{1}}}\right)}^{2}}\right]}^{\frac {1}{2}}}\right\}\\\end{aligned}}$

مثال2)

محاسبه ضریب دید برای دو کره که یکی درون دیگری قرار گرفته است:

${\begin{aligned}&F_{11}=0\\&F_{11}+F_{12}=1\,\,\,\to \,\,\,F_{12}=1\\&A_{2}F_{21}=A_{1}F_{12}\,\,\,\to \,\,\,F_{21}={\frac {A_{1}}{A_{2}}}=\left({\frac {D_{1}}{D_{2}}}\right)^{2}\\&F_{21}+F_{22}=1\,\,\,\to \,\,\,F_{22}=1-{\frac {A_{1}}{A_{2}}}\\\end{aligned}}$

_________________________________________________________________________________________________________________

مثال3) :

ضریب دید سطوح مثلث متساوی الاضلاع داده شده را بیابید؟ ${\begin{aligned}&{{F}_{11}}+{{F}_{12}}+{{F}_{13}}=1\mapsto {{F}_{11}}=0\Rightarrow {{F}_{12}}+{{F}_{13}}=1\\&{{F}_{21}}+{{F}_{22}}+{{F}_{23}}=1\mapsto {{F}_{22}}=0\Rightarrow {{F}_{21}}+{{F}_{23}}=1\\&{{F}_{31}}+{{F}_{32}}+{{F}_{33}}=1\mapsto {{F}_{33}}=0\Rightarrow {{F}_{31}}+{{F}_{32}}=1\\&\\&{{A}_{1}}{{F}_{12}}={{A}_{2}}{{F}_{21}}\\&{{A}_{2}}{{F}_{23}}={{A}_{3}}{{F}_{32}}\\&{{A}_{3}}{{F}_{31}}={{A}_{1}}{{F}_{13}}\\\end{aligned}}$

مثال4):

دو صفحه عمود بر هم بی نهایت را در نظر بگیرید.اگر صفحه عمودی را 1 در نظر بگیریم ${\rm {F}}_{\rm {12}}$ را بدست آورید.

حل:

یک سطح سوم را در نظر میگیریم به شکلی که یک محفظه بسته تشکیل شود.

$A:{\rm {F}}_{\rm {11}}={\rm {F}}_{\rm {22}}={\rm {F}}_{\rm {33}}=0$

$B:{\rm {F}}_{\rm {11}}+{\rm {F}}_{\rm {12}}+{\rm {F}}_{\rm {13}}=1$

$C:{\rm {\ }}{\rm {F}}_{\rm {21}}+{\rm {F}}_{\rm {22}}+{\rm {F}}_{\rm {23}}=1$

$D:{\rm {\ }}{\rm {F}}_{\rm {31}}+{\rm {F}}_{\rm {32}}+{\rm {F}}_{\rm {33}}=1$

با ساده سازی معادلات بالا داریم:

${\rm {F}}_{\rm {12}}+{\rm {F}}_{\rm {13}}=1$

${\rm {F}}_{\rm {21}}+{\rm {F}}_{\rm {23}}=1$

${\rm {F}}_{\rm {32}}+{\rm {F}}_{\rm {31}}=1$

حال از قانون عکس استفاده می کنیم:

$E:{\rm {L}}_{\rm {1}}{\rm {F}}_{\rm {12}}={\rm {L}}_{\rm {2}}{\rm {F}}_{\rm {21}}$

$F:{\rm {L}}_{\rm {1}}{\rm {F}}_{\rm {13}}={\rm {L}}_{\rm {3}}{\rm {F}}_{\rm {31}}$

$G:{\rm {\ }}{\rm {L}}_{\rm {2}}{\rm {F}}_{\rm {23}}={\rm {L}}_{\rm {3}}{\rm {F}}_{\rm {32}}$

از این سه رابطه برای ساده کردن سه معادله قبل بهره می بریم:

${\rm {F}}_{\rm {12}}+{\rm {F}}_{\rm {13}}=1$

${\frac {{\rm {L}}_{\rm {1}}}{{\rm {L}}_{\rm {2}}}}{\rm {F}}_{\rm {12}}+{\rm {F}}_{\rm {23}}=1$

${\frac {{\rm {L}}_{\rm {1}}}{{\rm {L}}_{\rm {2}}}}{\rm {F}}_{\rm {12}}+{\rm {F}}_{\rm {23}}=1$

با رابطه اول یک دستگاه دو مجهولی ایجاد می کنیم:

${\frac {{\rm {L}}_{\rm {1}}}{{\rm {L}}_{\rm {2}}}}{\rm {F}}_{\rm {12}}+{\rm {F}}_{\rm {23}}=1$

${\frac {{\rm {L}}_{\rm {1}}}{{\rm {L}}_{\rm {3}}}}{\rm {(1-F}}_{\rm {12}})+{\frac {{\rm {L}}_{\rm {2}}}{{\rm {L}}_{\rm {3}}}}{\rm {F}}_{\rm {23}}=1$

حال باحذف یک مجهول از دستگاه داریم:

${\frac {{\rm {L}}_{\rm {1}}}{{\rm {L}}_{\rm {3}}}}{\rm {(1-F}}_{\rm {12}})+{\frac {{\rm {L}}_{\rm {2}}}{{\rm {L}}_{\rm {3}}}}\left[{\rm {1-}}{\frac {{\rm {L}}_{\rm {1}}}{{\rm {L}}_{\rm {2}}}}{\rm {F}}_{\rm {12}}\right]=1$

${\rm {F}}_{\rm {12}}{\rm {=}}{\frac {{\rm {L}}_{\rm {1}}{\rm {+}}{\rm {L}}_{\rm {2}}{\rm {-}}{\rm {L}}_{\rm {3}}}{{\rm {2}}{\rm {L}}_{\rm {1}}}}$

که در اینجا

${\rm {L}}_{\rm {3}}={\left[{\rm {L}}_{\rm {1}}^{\rm {2}}{\rm {+}}{\rm {L}}_{\rm {2}}^{\rm {2}}\right]}^{\frac {\rm {1}}{\rm {2}}}$

_________________________________________________________________________________________________

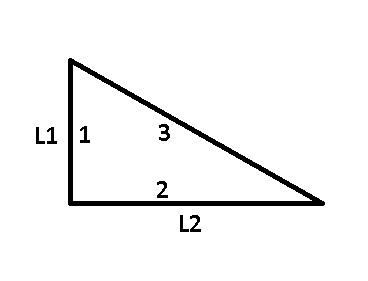
مثال5) برای شکل زیر $F_{12}$ را بدست آورید.

${\begin{aligned}&F_{11}=0\,\,\,,\,\,\,F_{22}=0\,\,\,,\,\,\,F_{33}=0\\&F_{11}+F_{12}+F_{13}=1\\&F_{21}+F_{22}+F_{23}=1\\&F_{31}+F_{32}+F_{33}=1\\&L_{1}F_{12}=L_{2}F_{21}\\&L_{1}F_{13}=L_{3}F_{31}\\&L_{2}F_{23}=L_{3}F_{32}\\&F_{12}={\frac {L_{1}+L_{2}-L_{3}}{2L_{1}}}\\\end{aligned}}$

_________________________________________________________________________________________________________________

مثال6): مقدار ${\rm {F}}_{\rm {12}}$ را بیابید.

حل: یک سطح کمکی میگیریم به طول 2L آن را ${\rm {L}}_{\rm {3}}$ مینامیم. فاصله خالی را ${\rm {L}}_{\rm {4}}$ مینامیم. از مثال قبل نیز استفاده میکنیم.

${\rm {F}}_{\rm {13}}{\rm {=}}{\frac {{\rm {L+2L-}}{\sqrt {\rm {5L}}}}{{\rm {2}}{\rm {L}}}}$

${\rm {F}}_{\rm {13}}{\rm {=}}{\rm {F}}_{\rm {14}}{\rm {+}}{\rm {F}}_{\rm {12}}$

${\rm {F}}_{\rm {14}}={\frac {{\rm {L+L-}}{\sqrt {\rm {2L}}}}{{\rm {2}}{\rm {L}}}}=1-{\frac {\sqrt {\rm {2}}}{2}}$

${\rm {F}}_{\rm {13}}{\rm {-}}{\rm {F}}_{\rm {14}}{\rm {=}}{\rm {F}}_{\rm {12}}$

${\rm {F}}_{\rm {12}}{\rm {=}}{\frac {{\rm {1-}}{\sqrt {\rm {5}}}{\rm {+}}{\sqrt {\rm {2}}}}{\rm {2}}}$

_________________________________________________________________________________________________________________

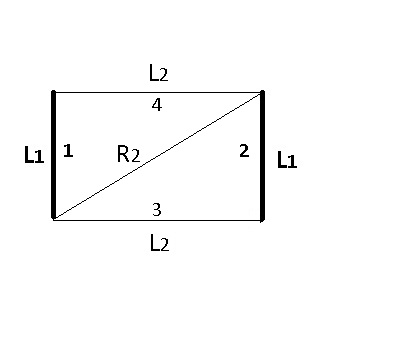
مثال7) برای شکل زیر $F_{12}$ را بدست آورید.

با تشکیل یک محفظه بسته مستطیلی شکل می توان قانون جمع را نوشت:

$F_{11}+F_{12}+F_{13}+F_{14}=1$

با رسم خط فرضی $R$ یک مثلث تشکیل داده و خواهیم داشت:

$F_{13}={\frac {L_{1}+L_{2}-R_{1}}{2L_{1}}}\,\,\,\,\,,\,(R_{1}={\sqrt {L_{1}^{2}+L_{2}^{2}}})$

به شکلی مشابه مطابق شکل خط $R_{2}$ را رسم کرده و خواهیم داشت:

$_{F_{14}={\frac {L_{1}+L_{2}-R_{2}}{2L_{1}}}\,\,\,\,\,,\,(R2={\sqrt {L_{1}^{2}+L_{2}^{2}}})}\,\,\,\,\,$

و نهایتا با توجه به اینکه $F_{11}=0$ خواهیم داشت:

$F_{12}=1-{\frac {L_{1}+L_{2}-{\sqrt {L_{1}^{2}+L_{2}^{2}}}}{L_{1}}}={\sqrt {1+\left({\frac {L_{2}}{L_{1}}}\right)^{2}}}\,\,-\,{\frac {L_{2}}{L_{1}}}$

_________________________________________________________________________________________________________________

مثال8) برای شکل زیر $F_{12}$ و $F_{22}$ را محاسبه کنید.

با استفاده از جدول 1-13 کتاب انتقال حرارت اینکروپرا (ویرایش چهارم) ضریب دید برای دو دیسک موازی هم محور به طریق زیر محاسبه می شود:

${\begin{aligned}&R_{j}={\frac {r_{j}}{L}}=0.25\\&S=1+{\frac {1+R_{j}^{2}}{R_{i}^{2}}}=18\\&F_{ij}=F_{13}={\frac {1}{2}}\left[S-\left[S^{2}-4\left({r_{j}}/{r_{i}}\;\right)^{2}\right]^{\frac {1}{2}}\right]=0.056\\\end{aligned}}$

با نوشتن قانون جمع:

${\begin{aligned}&F_{11}+F_{12}+F_{13}=1\\&F_{11}=0\\&F_{12}=1-F_{13}=0.944\\\end{aligned}}$

${\begin{aligned}&F_{11}+F_{12}+F_{13}=1\\&F_{11}=0\\&F_{12}=1-F_{13}=0.944\\\end{aligned}}$

${\begin{aligned}&F_{21}+F_{22}+F_{23}=1\\&A_{2}F_{21}=A_{1}F_{12}\,\,\,\to \,\,\,F_{21}={\frac {{\frac {\pi }{4}}D^{2}}{\pi DL}}F_{12}=0.944\\\end{aligned}}$

از تقارن خواهیم داشت:

$F_{23}=F_{21}$

$F_{22}=1-2F_{21}=0.764$

_________________________________________________________________________________________________

مثال9)در صورتی که ضریب دید تشعشعی بین دو صفحه بالا و پایین یک مکعب برابر 0.25 باشد ضریب دید صفحه بالایی مکعب با یکی از صفحات جانبی چقدر می شود؟

ره حل سوال 1: بطور کلی در حل ضرایب دید برای سطوح مکعب شکل و کلیه سطوحی که به نوعی تقارن دارند اگر تقارن را درست تشخیص دهیم مسئله خیلی ساده حل می شود: سطح بالایی مکعب را سطح شماره 1 سطح پایین مکعب را سطح شماره 2 و سطوح جانبی را شماره 3 تا 6 نامگذاری می کنیم از قانون جمع داریم:

${{F}_{11}}+{{F}_{12}}+{{F}_{13}}+{{F}_{14}}+{{F}_{15}}+{{F}_{16}}=1$

میدانیم : ${{F}_{11}}=0$

از طرفی به لحاظ تقارن داریم: ${{F}_{13}}={{F}_{14}}={{F}_{15}}={{F}_{16}}$

بنابر این :

$0.25-4{{F}_{13}}=1$

${{F}_{13}}={\frac {3}{16}}$