ویکیجزوه/دانشکده:فنی و مهندسی/مکانیک سیالات/میدان سرعت و شتاب در سیال
استاتيك سيالات كه در بخشهاي قبل بحث شد تقريبا علم دقيقي است و تنها كميتي كه نياز به آزمايش دارد وزن مخصوص است. از طرف ديگر طبيعت جريان يك سيال حقيقي بسيار پيچيده است و به آساني نمي توان قوانين اساسي توصيف كننده حركت كامل يك سيال را به روابط رياضي تبديل كرده و مورد استفاده قرار داد. در اين بخش استفاده از آزمايشات تجربي ضروري است.
منظور از میدان سرعت یک سیال چیست؟
[ویرایش]منظور از میدان سرعت یک سیال چیست؟ آیا همان تصوری که از سرعت ذرات و اجسام صلب داریم، به مکانیک سیالات قابل تعمیم است؟ بیائید نگاهی مجدد به این ترکیب بیندازیم: «میدان سرعت سیال» که متشکل از سه مفهوم میدان، سرعت و سیال میباشد. ابتدا هریک از این واژهها را به تنهایی تعریف میکنیم و در انتها ترکیب آنها را که هدف اصلی ما در این مقاله میباشد مورد بررسی قرار میدهیم. «میدان»، طبق تعریف، توزیع پیوستهای از یک کمیت اسکالر، برداری و یا تانسوری است که با توابع پیوستهای از مختصات فضا و زمان بیان شود. برای نمونه میتوان بیان نمود.
یک میدان برداری، مانند T(x, y, z, t) دمای تمام نقاط یک جسم را در هر لحظه با میدان اسکالر نشان داد. در مکانیک سیالات یک محیط پیوسته، V(x, y, z, t) میدان سرعت را م یتوان بصورت ریاضی کمیاتی مانند چگالی، دما، انرژی داخلی و آزاد، انتروپی، سرعت، تنش و ... به سیال نسبت داده م یشوند. فرض میشود که این کمیات، توابع پیوسته و همواری (مشتق پذیری) از متغیرهای فضایی و در گذر زمان میباشند. یعنی این کمیات میدانها هستند. از طرف دیگر فرض پیوستگی برای این توابع به همراه فرض هموار بودن به این معناست که تابع مورد نظر به تعداد بارهای دلخواه (معمولاً از نگاه کاربردی ۲ تا ۳ بار کافی است) برحسب تمام متغیرهای مستقل (۳ متغیر فضایی و ۱ متغیر زمان در کلی ترین حالت) قابل مشتقگیری است. چون دانش مکانیک سیالات با کمیات توزیع شده سروکار دارد، در آن فرصتهای زیادی برای استفاده سودمندانه از روش میدان وجود دارد. علاوه براین، میدانهای اسکالر، برداری و تانسوری در مطالعهٔ جنبههای گوناگون پدیدههای سیالات ظاهر میشوند.
ديدگاههای مطالعه حركت سيال
[ویرایش]ديدگاههای مطالعه حركت سيال
در تحلیل مسائل علم مکانیک ، دو دیدگاه وجود دارد : ديدگاه اویلری و ديدگاه لاگرانژی
در تحلیل مسایل علم مکانیک دو دیدگاه "اویلری" و "لاگرانژی" وجود دارد. در تحلیل مسایل مربوط به علم مکانیک سیالات از دیدگاه اویلری بهره میگیریم و درتحلیل مسایل مربوط به علم مکانیک جامدات از دیدگاه لاگرانژی سود میجوییم.
برای تحلیل جریان سه روش داریم 1.حجم کنترل یا تحلیل انتگرالی 2.سیستمهای بی نهایت کوچک یا تحلیل دیفرانسیلی 3.مطالعه آزمایشگاهی یا تحلیل ابعادی
برای هر کدام از این روشها جریان باید از قانون بقا در جرم-قانون بقا در اندازه حرکت خطی-قانون بقا در اندازه حرکت زاویه ای-قانون بقا در انرژی و همچنین حالت ترمودینامیکی و شرایط مرزی مناسب بیروی کند.
ما در اینجا روش اول یعنی حجم کنترل را مورد بررسی قرار میدهیم حجم کنترل در علم مکانیک سیالات همان نمودار جسم آزاد(F.B.D) برای اجسام صلب در علکم مکانیک جامدات است.در واقع حجم کنترل ناحیهٔ بسته ای است در آن مرزها بخاطر ورود و خروج جرم و اندازه حرکت و انرژی بسیار اهمیت دارند. در این روش حجم کنترل میتواند ساکن-متحرک با سرعت ثابت و یا متحرک با سرعت متغیر باشد که در اینحالت معادلات بیچیده میشوند 1.قانون بقا در جرم:Mc.v/∂t =∑Mi-∑Mo∂
که در این رابطه Mcv جرم حجم کنترل انتخابی و Miنرخ جرم ورودی و Mo نرخ جرم خروجی از حجم کنترل است. 2.قانون بقا در اندازه تکانه خطی:(MV)cv/∂t =∑(MV)i -∑(MV)o +∑F∂
که در این رابطه(MV)cv تکانه خطی حجم کنترل و(MV)i نرخ تکانه خطی ورودی به حجم کنترل و
MV)o) نرخ تکانه خطی خروجی از حجم کنترل است و F∑ مجموع نیروهای وارد بر حجم کنترل است 3.قانون بقا در اندازه تکانه زاویه ای:∂(Mr*V)cv/∂t =∑(Mr*V)i - ∑(Mr*V)o +∑Mo که در این رابطه(Mr*V)cv تکانه زاویه ای حجم کنترل و (Mr*V)I نرخ تکانه زاویه ای ورودی و(Mr*V)o نرخ تکانه زاویه ای خروجی Mo ∑ مجموع گشتاورهای وارد بر حجم کنترل است
ديدگاه اویلری
[ویرایش]دیدگاه اول که مناسب مکانیک سیالات است میدان جریان را مورد توجه قرار می دهد و به بیان اویلری (Eulerian) معروف است .در این روش آنچه برای ما مهم است این است که در زمان مورد نظر مقدار فشار،سرعت و شتاب و... هر ذره ای که در آن نقطه قرار دارد چقدر است .در این روش ، میدان فشار جریان (p(x,y,z,t محاسبه می گردد ، نه تغییرات فشار (p(t که بر یک ذره در حال عبور در میدان اعمال می شود .
اگر نقطه ثابتی را در فضا به مختصات x,y,z در نظر بگيريم، سرعت ذرات گذرنده از اين نقاط در هر لحظه را مي توان با استفاده از ميدان سرعت (v(x,y,z,t بدست آورد. به اين روش كه در يك نقطه ثابت از فضا سرعتهای رشته پيوسته ای از ذرات سيال كه از آن نقطه می گذرند اندازه گرفته مي شود، ديدگاه اویلری گفته می شود .
دیدگاه لاگرانژی
[ویرایش]دیدگاه دوم که یک ذره انفرادی متحرک را در میدان جریان دنبال میکند، به بیان لاگرانژی معروف است. روش لاگرانژی (Lagrangian) که بیشتر مناسب مکانیک جامدات است.
در دیدگاه لاگرانژی، حرکت هر یک از ذرات سیال را با دنبال کردن آن ذره تعقیب میکنیم. در این حالت برای هر یک از ذرات سیال سه تابع زمانی (x) ، (y) ، (z) را خواهیم داشت که در حالت کلی با توابع زمانی سایر ذرات متفاوت است. x(0) ،y(0) ،z(0) ، موقعیت اولیه ذره را در لحظه t=۰ نشان میدهد. با تمرکز بر روی هر یک از ذرات:
که برای هر ذره تنها تابعی از t است.
در توصیف لاگرانژ برای توصیف عمومی و کامل حرکت سیال مسیر تعداد بسیار بسیار زیادی از ذرات سیال باید مشخص گردد به همین دلیل اگر چه هر دو دیدگاه در دینامیک سیالات بکار میروند، در اکثر مسائل جریانهای سیال توصیف اویلری استفاده میشود.
دو دیدگاه اویلری و لاگرانژی به دائمی یا غیر دائمی بودن جریان بستگی ندارد.
میدان سرعت
[ویرایش]مهمترین مشخصه ی یک جریان که سایر مشخصات به آن وابسته است،سرعت است.
سرعت یک تابع برداری ازمکان است که درحالت سه بعدی سه مولفه دارد:
V (x,y,z,t) = u (x,y,z,t)i + v(x,y,z,t)j + w(x,y,z,t)k
شتاب يك ذره جريان
[ویرایش]شتاب يك ذره سيال برابر با نرخ تغيير سرعت ذره است. در صورت استفاده از ديدگاه لاگرانژی، مسير حركت ذره تعقيب مي شود. شتاب ذره از دو بار مشتق گيري بردار تغيير مكان بدست مي آيد و تنها تابعي از زمان است.
رویکرد لاگرانژی
بنابراين در ديدگاه لاگرانژی جهت تعيين سرعت در نقطه ای از ميدان جريان بايد مسير حركت ذره ای كه از نقطه مورد نظر می گذرد مشخص شده و سرعت از مشتق تغيير مكان بدست آيد. واضح است كه كاربرد اين روش براي تعيين سرعت يك نقطه دلخواه ميدان جريان بسيار پر زحمت است*
رویکرد اویلری
در ديدگاه اویلری، شتاب تابعی از زمان و مكان است يعنی شتاب رشته ذراتی كه در لحظه tاز موقعیت مکانی x,y,zعبور میکند .
مثال ۱
[ویرایش]یک میدان برداری سرعت اویلری به این شکل داده شده است:
شتاب در لحظه t=1 s و در مکان x=2 m برای این میدان به دست آورید.
جواب:
مثال ۲
[ویرایش]میدان برداری سرعت اویلری به شکل زیر داده شده است :
(1,1,0)a را بدست آورید .
جواب :
توجه کنید که:
مثال ۳
[ویرایش]اگر باشد شتاب را بر حسب x بدست آورید:
مثال ۴
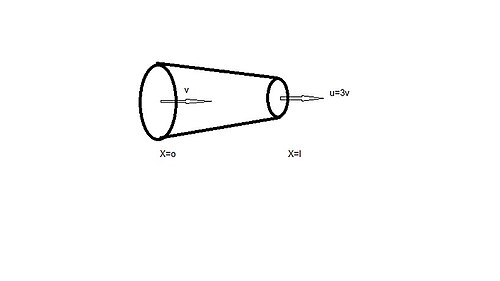
[ویرایش]اگر
باشد
الف) شتاب را بر حسب x بدست آورید؟
ب) مدت زمانی که از x=۰ به x=l میرسد؟
ج) اگر
جریان تراکم پذیر هست یا تراکم ناپذیر؟
حل
- الف)
بر اساس رابطه اویلر aرا برحسب x بدست میآوریم:
- ب)
- ج)
اگر باشد تراکم ناپذیر میباشد در غیر اینصورت تراکم پذیر میباشد.
چون
پس تراکم پذیر میباشد.






















