نگاهی به ریاضیات پیشرفته/هندسه

هِندِسه(یا ژِئو «زمین»، مِتریا «سنجش، اندازه‌گیری») شاخه‌ای از ریاضیات است که با شکل، اندازه، موقعیت نسبی شکل‌ها و ویژگی‌های فضا سروکار دارد. ریاضیدانی که در شاخهٔ هندسه کار می‌کند هندسه‌دان نامیده می‌شود. هندسه به‌طور مستقل در پاره‌ای از تمدن‌های اولیه به شکل بدنه‌ای از دانش عملی در مورد طول، مساحت و حجم ظهور کرد و پایه‌ریزی آن به عنوان یک دانش رسمی ریاضی در زمان تالس (قرن ششم پیش از میلاد) در غرب آغاز شد. در قرن سوم پیش از میلاد، هندسه توسط اقلیدس به شکل اصل موضوعی درآمده بود و کار اقلیدس (هندسه اقلیدسی) استانداردی را پایه‌ریزی نمود که قرن‌ها دنبال شد. ارشمیدس روش‌های هوشمندانه‌ای برای محاسبهٔ مساحت و حجم ارائه داد که در بسیاری موارد پیش‌رو حساب انتگرال جدید محسوب می‌شوند. دانش اخترشناسی و به ویژه نگاشتن مکان ستاره‌ها و سیاره‌ها روی کره آسمان و توصیف رابطهٔ بین حرکت اجسام آسمانی تا هزار و پانصد سال بعد منشا بسیاری از پرسش‌های هندسی بود. هر دوی هندسه و اخترشناسی در دنیای کلاسیک بخشی از کوادریویم بودند که خود زیرمجموعه‌ای از علوم مقدماتی هفتگانه بود که یادگیری آن‌ها برای هر شهروند آزادی ضروری می‌نمود.

تاریخ[ویرایش]

اولین آغاز ثبت شده هندسه را می توان در بین النهرین باستان و مصر در هزاره دوم قبل از میلاد ردیابی کرد. هندسه اولیه مجموعه ای از اصول کشف شده تجربی در مورد طول ها، زوایا، مساحت ها و حجم ها بود که برای رفع برخی نیازهای عملی در نقشه برداری ، ساخت و ساز ، نجوم و صنایع دستی مختلف توسعه یافت. اولین متون شناخته شده در مورد هندسه عبارتند از پاپیروس رایند مصر (2000-1800 قبل از میلاد) و پاپیروس مسکو (حدود 1890 قبل از میلاد) و الواح گلی بابلی ، مانند Plimpton 322 .(1900 قبل از میلاد). به عنوان مثال، پاپیروس مسکو فرمولی برای محاسبه حجم یک هرم کوتاه شده یا فروستوم ارائه می دهد. لوح‌های گلی بعدی (350–50 قبل از میلاد) نشان می‌دهد که اخترشناسان بابلی روش‌های ذوزنقه‌ای را برای محاسبه موقعیت و حرکت مشتری در فضای سرعت-زمان اجرا کردند. این رویه‌های هندسی ماشین‌حساب‌های آکسفورد ، از جمله قضیه سرعت متوسط را تا 14 قرن پیش‌بینی کردند. در جنوب مصر، نوبیای باستان سیستمی از هندسه شامل نسخه‌های اولیه ساعت‌های خورشیدی ایجاد کردند.

در قرن هفتم قبل از میلاد، ریاضیدان یونانی تالس اهل میلتوس از هندسه برای حل مسائلی مانند محاسبه ارتفاع اهرام و فاصله کشتی ها از ساحل استفاده کرد. او را با اولین استفاده از استدلال قیاسی به کار رفته در هندسه، با استخراج چهار نتیجه به قضیه تالس، نسبت می دهند. فیثاغورث مکتب فیثاغورث را تأسیس کرد ، که اولین اثبات قضیه فیثاغورث به آن نسبت داده می شود ، اگرچه بیان این قضیه سابقه طولانی دارد. Eudoxus (408-حدود 355 قبل از میلاد) روش فرسودگی را توسعه داد.که امکان محاسبه مساحت ها و حجم ارقام منحنی را فراهم می کند، و همچنین نظریه نسبت هایی که از مشکل قدرهای غیرقابل مقایسه جلوگیری می کند ، که هندسه های بعدی را قادر می سازد پیشرفت های قابل توجهی داشته باشند. در حدود 300 سال قبل از میلاد، هندسه توسط اقلیدس متحول شد، او که «عناصرش» که به طور گسترده‌ای موفق‌ترین و تأثیرگذارترین کتاب درسی در تمام دوران به شمار می‌رود، دقت ریاضی را از طریق روش بدیهی معرفی کرد و اولین نمونه از قالبی است که امروزه در ریاضیات استفاده می‌شود. تعریف، بدیهیات، قضیه و برهان. اگر چه بیشتر مطالب عناصرقبلاً شناخته شده بودند، اقلیدس آنها را در یک چارچوب منطقی واحد و منسجم مرتب کرد. عناصر تا اواسط قرن بیستم برای همه تحصیلکرده‌های غرب شناخته شده بود و امروزه نیز مطالب آن در کلاس‌های هندسه تدریس می‌شود . ارشمیدس (حدود 287-212 قبل از میلاد) سیراکوزی از روش خستگی برای محاسبه مساحت زیر کمان سهمی با جمع یک سری نامتناهی استفاده کرد و تقریب‌های دقیقی از پی ارائه کرد. او همچنین مارپیچ نام خود را مطالعه کرد و فرمول هایی برای آن به دست آوردحجم سطوح انقلاب ریاضیدانان هندی نیز سهم مهمی در هندسه داشتند. Satapatha Brahmana (قرن 3 قبل از میلاد) شامل قوانینی برای ساخت و سازهای هندسی آیینی است که شبیه به Sulba Sutras است. بر اساس ( هایاشی 2005 ، ص 363)، سوتراهای اولبا حاوی "قدیمی ترین بیان شفاهی موجود از قضیه فیثاغورث در جهان است، اگرچه قبلاً برای بابلیان قدیم شناخته شده بود. آنها حاوی فهرست هایی از سه گانه فیثاغورثی هستند. که موارد خاصی از معادلات دیوفانتین است [ در نسخه خطی بخشعلیتعداد انگشت شماری از مسائل هندسی (از جمله مسائل مربوط به حجم جامدات نامنظم) وجود دارد. نسخه خطی بخشعلی نیز «نظام ارزش اعشاری با نقطه صفر را به کار می گیرد». Aryabhatiya Aryabhata ( 499) شامل محاسبه مساحت و حجم است. براهماگوپتا اثر نجومی خود را براهما اسفوتا سیدانتا در سال 628 نوشت. فصل 12، شامل 66 آیه سانسکریت ، به دو بخش تقسیم شد: "عملیات اساسی" (شامل ریشه های مکعب، کسرها، نسبت و نسبت، و مبادله مبادله ای) و "عملیات مبادله ای". مخلوط، سری های ریاضی، ارقام هواپیما، روی هم چیدن آجرها، اره کردن الوار، و انباشته شدن دانه ها). در بخش دوم، او قضیه معروف خود را در مورد قطرهای یک چهارضلعی حلقوی بیان کرد. فصل 12 همچنین شامل فرمولی برای مساحت چهارضلعی حلقوی (تعمیم فرمول هرون )، و همچنین توضیح کاملی از مثلث های گویا ( یعنی مثلث هایی با اضلاع گویا و مساحت های گویا) بود.

در قرون وسطی ، ریاضیات در اسلام قرون وسطی به توسعه هندسه، به ویژه هندسه جبری کمک کرد. المهانی (متولد 853) ایده کاهش مسائل هندسی مانند تکرار مکعب به مسائل جبر را در ذهن داشت. ثابت بن قره (معروف به لاتین به عنوان Thebit ) (901-836) با عملیات حسابی که برای نسبت‌های کمیت‌های هندسی اعمال می‌شود، سروکار داشت و به توسعه هندسه تحلیلی کمک کرد. عمر خیام (1048-1131) راه حل های هندسی معادلات مکعبی را یافت.. قضایای ابن هیثم (الحازن)، عمر خیام و نصیرالدین طوسی در مورد چهارضلعی ها، از جمله چهارضلعی لامبرت و چهارضلعی ساکری ، نتایج اولیه در هندسه هذلولی بود و همراه با فرض های جایگزین آنها، مانند به عنوان بدیهیات Playfair ، این آثار تأثیر قابل توجهی بر توسعه هندسه غیر اقلیدسی در میان هندسه‌سنج‌های بعدی اروپایی، از جمله Witelo (حدود 1230-حدود 1314)، جرسونیدس (1288-1344)، آلفونسو ، جان والیس ، و جیووانی گیرولامو داشتند. ساچری.

در اوایل قرن هفدهم، دو پیشرفت مهم در هندسه رخ داد. اولین مورد ایجاد هندسه تحلیلی، یا هندسه با مختصات و معادلات ، توسط رنه دکارت (1596-1650) و پیر دو فرما (1601-1665) بود. این یک پیش درآمد ضروری برای توسعه حساب دیفرانسیل و انتگرال و علم کمی دقیق فیزیک بود. دومین توسعه هندسی این دوره، مطالعه سیستماتیک هندسه تصویری توسط ژیرار دسارگ (1591-1661) بود. هندسه فرافکنی به بررسی خواص اشکالی می‌پردازد که در زیر بدون تغییر هستندطرح‌ها و بخش‌ها ، به‌ویژه که به دیدگاه هنری مربوط می‌شوند .

دو پیشرفت در هندسه در قرن نوزدهم روش مطالعه قبلی آن را تغییر داد. اینها کشف هندسه های غیراقلیدسی توسط نیکولای ایوانوویچ لوباچفسکی، یانوس بولیای و کارل فردریش گاوس و فرمول بندی تقارن به عنوان ملاحظات اصلی در برنامه ارلانگن فلیکس کلاین (که اقلیدسی و غیر اقلیدسی را تعمیم داد) بود. ). دو تن از هندسه‌دانان چیره دست آن زمان برنهارد ریمان (1826-1866) بودند که عمدتاً با ابزارهایی از آنالیز ریاضی کار می‌کردند و سطح ریمان را معرفی می‌کردند ، و هانری پوانکاره ، بنیان‌گذارتوپولوژی جبری و نظریه هندسی سیستم های دینامیکی . در نتیجه این تغییرات عمده در مفهوم هندسه، مفهوم "فضا" به چیزی غنی و متنوع تبدیل شد و زمینه طبیعی تئوری هایی مانند تحلیل پیچیده و مکانیک کلاسیک متفاوت شد.

مفاهیم مهم اصلی[ویرایش]

بدیهیات[ویرایش]

اقلیدس در کتاب عناصر خود که یکی از تأثیرگذارترین کتاب‌هایی است که تا کنون نوشته شده است ، رویکردی انتزاعی به هندسه داشت . اقلیدس بدیهیات یا فرضیه های خاصی را معرفی کرد که ویژگی های اولیه یا بدیهی نقاط، خطوط و سطوح را بیان می کرد. او با استدلال ریاضی به استنباط دقیق سایر خصوصیات پرداخت. ویژگی بارز رویکرد اقلیدس به هندسه سختی آن بود و به هندسه بدیهی یا ترکیبی معروف شد . در آغاز قرن 19، کشف هندسه های غیر اقلیدسی توسطنیکولای ایوانوویچ لوباچفسکی (1792-1856)، یانوس بولیای (1802-1860)، کارل فردریش گاوس (1777-1855) و دیگران منجر به احیای علاقه به این رشته شدند و در قرن بیستم، دیوید هیلبرت (186) -1943) از استدلال بدیهی در تلاش برای ارائه یک پایه مدرن از هندسه استفاده کرد.

ویژگی بارز رویکرد اقلیدس به هندسه سختی آن بود و به هندسه بدیهی یا ترکیبی معروف شد . در آغاز قرن 19، کشف هندسه های غیر اقلیدسی توسطنیکولای ایوانوویچ لوباچفسکی (1792-1856)، یانوس بولیای (1802-1860)، کارل فردریش گاوس (1777-1855) و دیگران منجر به احیای علاقه به این رشته شدند و در قرن بیستم، دیوید هیلبرت (186) -1943) از استدلال بدیهی در تلاش برای ارائه یک پایه مدرن از هندسه استفاده کرد.

اشیاء[ویرایش]

نکته ها[ویرایش]

نقاط عموماً اشیاء اساسی برای هندسه ساختمان در نظر گرفته می شوند. آنها ممکن است با خواصی که باید داشته باشند تعریف شوند، مانند تعریف اقلیدس به عنوان "آنچه که جزئی ندارد" یا در هندسه مصنوعی . در ریاضیات مدرن، آنها به طور کلی به عنوان عناصر مجموعه ای به نام فضا تعریف می شوند که خود به صورت بدیهی تعریف شده است.

با این تعاریف مدرن، هر شکل هندسی به عنوان مجموعه ای از نقاط تعریف می شود. این مورد در هندسه مصنوعی نیست، جایی که یک خط یک شی بنیادی دیگر است که به عنوان مجموعه نقاطی که از آن عبور می کند دیده نمی شود.

با این حال، هندسه های مدرنی وجود دارد که در آن نقاط، اشیاء ابتدایی یا حتی بدون نقطه نیستند. یکی از قدیمی‌ترین این هندسه‌ها، هندسه بدون نقطه وایتهد است که توسط آلفرد نورث وایتهد در سال‌های 1919-1920 فرموله شد.

خطوط[ویرایش]

اقلیدس خطی را به عنوان "طول بی عرض" توصیف کرد که "به طور مساوی نسبت به نقاط روی خود قرار دارد". در ریاضیات مدرن، با توجه به انبوه هندسه ها، مفهوم خط با نحوه توصیف هندسه پیوند نزدیکی دارد. به عنوان مثال، در هندسه تحلیلی ، یک خط در صفحه اغلب به عنوان مجموعه نقاطی تعریف می شود که مختصات آنها معادله خطی معینی را برآورده می کند ، اما در یک محیط انتزاعی تر، مانند هندسه وقوع ، یک خط ممکن است یک شی مستقل باشد. ، متمایز از مجموعه نقاطی که روی آن قرار دارند. در هندسه دیفرانسیل، ژئودزیک تعمیم مفهوم خط بهفضاهای منحنی .

هواپیماها[ویرایش]

در هندسه اقلیدسی، صفحه یک سطح صاف و دو بعدی است که تا بی نهایت امتداد دارد. تعاریف برای انواع دیگر هندسه تعمیم آن است. صفحات در بسیاری از زمینه های هندسه استفاده می شوند. به عنوان مثال، صفحات را می توان به عنوان یک سطح توپولوژیکی بدون اشاره به فواصل یا زاویه مطالعه کرد. می‌توان آن را به‌عنوان یک فضای نزدیک مورد مطالعه قرار داد ، جایی که همخطی‌ها و نسبت‌ها را می‌توان مطالعه کرد اما فاصله‌ها را نه. می توان آن را به عنوان صفحه مختلط با استفاده از تکنیک های تحلیل پیچیده مطالعه کرد. و غیره.

زاویه[ویرایش]

اقلیدس زاویه صفحه را به عنوان تمایل به یکدیگر، در یک صفحه، از دو خط که یکدیگر را ملاقات می کنند و نسبت به یکدیگر مستقیم نیستند، تعریف می کند. در اصطلاح امروزی، زاویه شکلی است که توسط دو پرتو تشکیل شده است ، که اضلاع زاویه نامیده می‌شوند و نقطه پایانی مشترکی دارند که به آن راس زاویه می‌گویند

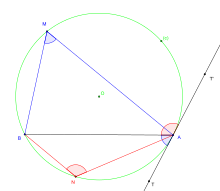
اقلیدس زاویه صفحه را به عنوان تمایل به یکدیگر، در یک صفحه، از دو خط که یکدیگر را ملاقات می کنند و نسبت به یکدیگر مستقیم نیستند، تعریف می کند. در اصطلاح امروزی، زاویه شکلی است که توسط دو پرتو تشکیل شده است ، که اضلاع زاویه نامیده می‌شوند و نقطه پایانی مشترکی دارند که به آن راس زاویه می‌گویند .

زوایای تند (الف)، مبهم (ب) و مستقیم (ج). زوایای تند و منفرد به زوایای مایل نیز معروف هستند.

در هندسه اقلیدسی ، از زاویه ها برای مطالعه چند ضلعی ها و مثلث ها و همچنین تشکیل یک شی مورد مطالعه به تنهایی استفاده می شود. مطالعه زوایای یک مثلث یا زوایای یک دایره ، اساس مثلثات را تشکیل می دهد.

در هندسه دیفرانسیل و حساب دیفرانسیل و انتگرال ، زوایای بین منحنی های صفحه یا منحنی های فضایی یا سطوح را می توان با استفاده از مشتق محاسبه کرد .

منحنی ها[ویرایش]

منحنی یک جسم 1 بعدی است که ممکن است مستقیم (مانند یک خط) باشد یا خیر. منحنی های فضای دوبعدی را منحنی های صفحه و منحنی های فضای سه بعدی را منحنی های فضایی می نامند .

در توپولوژی، منحنی با تابعی از بازه ای از اعداد واقعی تا فضای دیگر تعریف می شود. در هندسه دیفرانسیل، از همان تعریف استفاده می‌شود، اما تابع تعریف کننده باید قابل تمایز باشد هندسه جبری منحنی‌های جبری را مطالعه می‌کند که به عنوان انواع جبری بعد یک تعریف می‌شوند.

سطح[ویرایش]

سطح یک جسم دو بعدی است، مانند کره یا پارابولوئید. در هندسه دیفرانسیل و توپولوژی ، سطوح با «لکه‌های» دو بعدی (یا همسایگی‌ها ) توصیف می‌شوند که به ترتیب توسط دیفرمورفیسم‌ها یا همومورفیسم‌ها مونتاژ می‌شوند . در هندسه جبری، سطوح با معادلات چند جمله ای توصیف می شوند .

منیفولدها[ویرایش]

منیفولد تعمیم مفاهیم منحنی و سطح است. در توپولوژی ، منیفولد فضای توپولوژیکی است که در آن هر نقطه دارای یک همسایگی است است که با فضای اقلیدسی همومورف است . در هندسه دیفرانسیل ، منیفولد قابل تمایز فضایی است که در آن هر همسایگی با فضای اقلیدسی تفاوت دارد.

منیفولدها به طور گسترده در فیزیک از جمله در نسبیت عام و نظریه ریسمان استفاده می شوند.

طول، مساحت و حجم[ویرایش]

طول ، مساحت و حجم به ترتیب اندازه یا وسعت یک جسم را در یک بعدی، دو بعدی و سه بعدی توصیف می کنند.

که در هندسه اقلیدسی و هندسه تحلیلی ، طول یک پاره خط را اغلب می توان با قضیه فیثاغورث محاسبه کرد .

مساحت و حجم را می توان به عنوان کمیت های اساسی جدا از طول تعریف کرد یا می توان آنها را بر حسب طول در یک صفحه یا فضای سه بعدی توصیف و محاسبه کرد. ریاضیدانان فرمول های صریح بسیاری برای مساحت و فرمول های حجم اجسام مختلف هندسی یافته اند. در حساب دیفرانسیل و انتگرال ، مساحت و حجم را می توان بر حسب انتگرال تعریف کرد ، مانند انتگرال ریمان یا انتگرال لبگ است.

معیارها و سنجش ها[ویرایش]

مفهوم طول یا فاصله را می توان تعمیم داد و به ایده متریک منجر شد. برای مثال، متریک اقلیدسی فاصله بین نقاط در صفحه اقلیدسی را اندازه‌گیری می‌کند ، در حالی که متریک هذلولی فاصله را در صفحه هذلولی اندازه‌گیری می‌کند . از دیگر نمونه‌های مهم معیارها می‌توان به متریک لورنتز نسبیت خاص و معیارهای نیمه ریمانی نسبیت عام اشاره کرد.

در جهتی متفاوت، مفاهیم طول، مساحت و حجم توسط تئوری اندازه گیری گسترش می یابد که روش های تعیین اندازه یا اندازه را مطالعه می کند. به مجموعه‌ها را مطالعه می‌کند، که در آن معیارها از قوانینی مشابه مساحت و حجم کلاسیک پیروی می‌کنند.

همخوانی و تشابه[ویرایش]

همخوانی و شباهت مفاهیمی هستند که توصیف می کنند زمانی که دو شکل دارای ویژگی های مشابه هستند. در هندسه اقلیدسی، از تشابه برای توصیف اشیایی استفاده می‌شود که شکل یکسانی دارند، در حالی که همخوانی برای توصیف اجسامی که از نظر اندازه و شکل یکسان هستند، استفاده می‌شود. هیلبرت ، در کار خود در مورد ایجاد یک پایه دقیق تر برای هندسه، تطابق را به عنوان یک اصطلاح تعریف نشده که ویژگی های آن با بدیهیات تعریف می شود، در نظر گرفت .

همخوانی و شباهت در هندسه تبدیل تعمیم می یابد تعمیم می‌یابد، که به بررسی خواص اجسام هندسی می‌پردازد که توسط انواع مختلف تبدیل‌ها حفظ می‌شوند.

قطب نما و سازه های مستقیم[ویرایش]

هندسه‌سنج‌های کلاسیک به ساخت اجسام هندسی که به گونه‌ای دیگر توصیف شده‌اند، توجه ویژه‌ای داشتند. به طور کلاسیک، تنها ابزاری که در بیشتر سازه‌های هندسی استفاده می‌شود، قطب‌نما و راسته است. همچنین، هر ساخت و ساز باید در تعداد محدودی از مراحل تکمیل شود. با این حال، حل برخی از مشکلات به تنهایی با این ابزارها دشوار یا غیرممکن بود و ساختارهای مبتکرانه ای با استفاده از نئوسیس ، سهمی و سایر منحنی ها یا وسایل مکانیکی پیدا شد.

بعد،ابعاد،اندازه[ویرایش]

جایی که هندسه سنتی ابعاد0(یک نقطه) 1 (یک خط )، 2 ( صفحه ) و 3 (فضا) مجاز می کرد، ریاضیدانان و فیزیکدانان تقریباً دو قرن از ابعاد بالاتر استفاده کرده اند. یکی از نمونه‌های کاربرد ریاضی برای ابعاد بالاتر، فضای پیکربندی یک سیستم فیزیکی است که ابعادی برابر با درجه‌های آزادی سیستم دارد. به عنوان مثال، پیکربندی یک پیچ را می توان با پنج مختصات توصیف کرد.

در توپولوژی کلی ، مفهوم بعد از اعداد طبیعی به بعد بی نهایت ( مثلاً فضاهای هیلبرت ) و اعداد حقیقی مثبت (در هندسه فراکتال ) گسترش یافته است. در هندسه جبری ، بعد یک تنوع جبری تعدادی تعاریف ظاهراً متفاوت دریافت کرده است که همه در رایج‌ترین موارد معادل هستند.

نقطه،خط،صفحه،فضا[ویرایش]

نقطه[ویرایش]

در هندسه کلاسیک اقلیدسی ، نقطه یک مفهوم ابتدایی است که مکان دقیقی را در فضا مدل می‌کند و طول، عرض یا ضخامت ندارد. در ریاضیات مدرن ، یک نقطه به طور کلی به عنصری از مجموعه ای به نام فضا اشاره دارد.نقطه یک شی صفر بعدی است که با استفاده از آن فضای یک بعدی(خط)به وجود می آید

مفهوم ابتدایی بودن به این معنی است که یک نقطه را نمی توان بر حسب اشیاء تعریف شده قبلی تعریف کرد. به این معنا که یک نقطه فقط با برخی از ویژگی ها به نام بدیهیات تعریف می شود که باید آن ها را برآورده کند. به عنوان مثال، "دقیقا یک خط وجود دارد که از دو نقطه مختلف می گذرد" .

خط[ویرایش]

خط، امتداد نقطه است.

بر اثر حرکت و امتداد یک نقطه بر صفحه در یک راستا، خط شکل می‌گیرد.

خط در هندسه به‌معنی اتصال یا امتداد دو نقطه-در یک راستا-بر روی سطح (صفحه) که سطح را تقسیم می‌کند. خط به‌طور مطلق از دو جهت، بی‌نهایت امتداد دارد. نیم‌خط از یک نقطه، آغاز می‌شود و از دیگر سو بی‌نهایت امتداد دارد و پاره‌خط از هر دو سو به دو نقطه، محدود است.

در هندسهٔ اقلیدسی، خط، عبارت است از کوتاه‌ترین مسیر بین دو نقطه که ممکن است از هر جهت بی‌نهایت امتداد پیدا کند. از سویی پاره‌خط کوتاه‌ترین مسیر بین دو نقطه است.با استفاده از خط می توان صفحه درست کرد

صفحه[ویرایش]

به طور نامحدود گسترش می یابد. صفحه آنالوگ دو بعدی یک نقطه (ابعاد صفر)، یک خط (یک بعدی) و فضای سه بعدی است . صفحات می توانند به عنوان زیرفضاهای فضایی با ابعاد بالاتر، مانند یکی از دیوارهای اتاق، بی نهایت گسترش یافته باشند، یا ممکن است به تنهایی از وجود مستقلی برخوردار شوند،

فضا[ویرایش]

فضای سه بعدی (همچنین: فضای سه بعدی ، فضای سه بعدی یا به ندرت فضای سه بعدی ) یک تنظیم هندسی است که در آن سه مقدار (به نام پارامتر ) برای تعیین موقعیت یک عنصر (یعنی نقطه ) مورد نیاز است. این معنای غیر رسمی اصطلاح بعد است.

در ریاضیات ، چند عدد از n عدد را می توان به عنوان مختصات دکارتی یک مکان در فضای اقلیدسی n بعدی درک کرد. مجموعه این n- tuples معمولا نشان داده می شودو می توان آن را در فضای اقلیدسی n بعدی شناسایی کرد. وقتی n = 3 باشد، این فاصله فراخوانی می شودفضای اقلیدسی سه بعدی (یا به سادگی فضای اقلیدسی هنگامی که زمینه واضح است). این به عنوان مدلی از جهان فیزیکی عمل می کند (زمانی که نظریه نسبیت در نظر گرفته نمی شود)، که در آن تمام ماده شناخته شده وجود دارد. در حالی که این فضا متقاعدکننده‌ترین و مفیدترین راه برای مدل‌سازی جهان آن‌گونه که تجربه می‌شود، باقی می‌ماند، تنها نمونه‌ای از تنوع زیادی از فضاها در سه بعدی به نام 3 منیفولد است . در این مثال کلاسیک، هنگامی که سه مقدار به اندازه گیری در جهات مختلف ( مختصات ) اشاره دارد، هر سه جهت را می توان انتخاب کرد، مشروط بر اینکه بردارهادر این جهات همه در یک فضای 2 ( صفحه ) قرار نمی گیرند. علاوه بر این، در این مورد، این سه مقدار را می توان با هر ترکیبی از سه مورد انتخاب شده از عبارات عرض / عرض ، ارتفاع / عمق و طول برچسب گذاری کرد.

تقارن[ویرایش]

قدمت موضوع تقارن در هندسه به اندازه خود علم هندسه است. اشکال متقارن مانند دایره ، چند ضلعی های منظم و جامدات افلاطونی اهمیت عمیقی برای بسیاری از فیلسوفان باستان داشتند و قبل از زمان اقلیدس به تفصیل مورد بررسی قرار گرفتند. الگوهای متقارن در طبیعت اتفاق می‌افتند و به صورت هنرمندانه در بسیاری از اشکال، از جمله گرافیک لئوناردو داوینچی ، ام سی اسچر ، و دیگران ارائه شده‌اند. در نیمه دوم قرن 19، رابطه بین تقارن و هندسه مورد بررسی شدید قرار گرفت.برنامه ارلانگن فلیکس کلاین اعلام کرد که به معنای بسیار دقیق، تقارن، که از طریق مفهوم گروه تبدیل بیان می شود، تعیین می کند که هندسه چیست . تقارن در هندسه کلاسیک اقلیدسی با همخوانی‌ها و حرکات صلب نشان داده می‌شود ، در حالی که در هندسه تصویری نقش مشابهی توسط تلاقی‌ها ، تبدیل‌های هندسی ایفا می‌شود که خطوط مستقیم را به خطوط مستقیم تبدیل می‌کنند. اما در هندسه‌های جدید بولیایی و لوباچفسکی، ریمان، کلیفورد و کلاین، و سوفوس لی وجود داشت.ایده کلاین برای «تعریف هندسه از طریق گروه تقارن آن » الهام گرفته شده است. هر دو تقارن گسسته و پیوسته نقش برجسته ای در هندسه دارند، اولی در توپولوژی و نظریه گروه هندسی ، دومی در نظریه دروغ و هندسه ریمانی .

نوع متفاوتی از تقارن، اصل دوگانگی در هندسه تصویری ، در میان زمینه‌های دیگر است. این فراپدیده را می‌توان تقریباً به این صورت توصیف کرد: در هر قضیه ، نقطه مبادله با صفحه ، پیوستن به meet ، نهفته در با حاوی ، و نتیجه یک قضیه به همان اندازه درست است. شکل مشابه و نزدیک به دوگانگی بین فضای برداری و فضای دوگانه آن وجود دارد.

برنامه های کاربری[ویرایش]

هندسه در بسیاری از زمینه ها کاربرد پیدا کرده است که در زیر به برخی از آنها اشاره می شود.

هنر[ویرایش]

ریاضیات و هنر به طرق مختلفی با هم مرتبط هستند. برای مثال، تئوری پرسپکتیو نشان داد که هندسه چیزی بیش از ویژگی‌های متریک شکل‌ها دارد: پرسپکتیو منشأ هندسه تصویری است .

هنرمندان مدت‌هاست که از مفاهیم تناسب در طراحی استفاده می‌کنند. ویتروویوس یک نظریه پیچیده از تناسبات ایده آل برای پیکر انسان ایجاد کرد. این مفاهیم توسط هنرمندانی از میکل آنژ تا هنرمندان کمیک بوک مدرن استفاده و اقتباس شده است.

نسبت طلایی نسبت خاصی است که نقشی بحث برانگیز در هنر داشته است. اغلب ادعا می‌شود که از نظر زیبایی‌شناختی دلپذیرترین نسبت طول است، اغلب گفته می‌شود که در آثار هنری معروف گنجانده شده است، اگرچه قابل‌اعتمادترین و بدون ابهام‌ترین نمونه‌ها عمداً توسط هنرمندان آگاه از این افسانه ساخته شده است.

کاشی کاری یا تزیینات در طول تاریخ در هنر استفاده شده است. هنر اسلامی مانند هنر MC Escher به طور مکرر از تسلیحات استفاده می کند . کار اشر همچنین از هندسه هذلولی استفاده کرد.

سزان این نظریه را مطرح کرد که همه تصاویر را می توان از کره ، مخروط و استوانه ساخت . این هنوز هم امروزه در تئوری هنر استفاده می شود، اگرچه فهرست دقیق اشکال از نویسنده ای به نویسنده دیگر متفاوت است.

معماری[ویرایش]

هندسه کاربردهای زیادی در معماری دارد. در واقع، گفته شده است که هندسه در هسته طراحی معماری قرار دارد. کاربردهای هندسه در معماری شامل استفاده از هندسه تصویری برای ایجاد پرسپکتیو اجباری ، استفاده از مقاطع مخروطی در ساخت گنبدها و اشیاء مشابه، استفاده از تسلسل ، و استفاده از تقارن

فیزیک[ویرایش]

حوزه نجوم ، به ویژه از آنجایی که به نقشه برداری از موقعیت ستارگان و سیارات در کره سماوی و توصیف رابطه بین حرکات اجرام سماوی مربوط می شود، به عنوان منبع مهمی از مشکلات هندسی در طول تاریخ خدمت کرده است.

هندسه ریمانی و هندسه شبه ریمانی در نسبیت عام استفاده می شود . نظریه ریسمان از چندین نوع هندسه استفاده می کند، و همچنین نظریه اطلاعات کوانتومی .

منابع[ویرایش]

ویکی پدیای انگلیسی