نگاهی به ریاضیات پیشرفته/هندسه جبری

هندسهٔ جبری شاخه‌ای از ریاضیات است که به‌طور سنتی به مطالعهٔ صفرهای چندجمله‌ای های چند متغیره می‌پردازد. هندسهٔ جبری مدرن بر اساس استفاده از تکنیک‌های جبر مجرد بنا شده که اساساً از جبر جابجایی استفاده می‌کند تا مسائل هندسی مربوط به این مجموعه صفرها (ریشه این چند جمله‌ای‌ها) را مطالعه کند.

اشیای بنیادی که در مطالعه هندسه جبری استفاده می‌شوند واریته‌های جبری‌اند که بیان هندسی حل دستگاهی از معادلات چند جمله‌ای‌اند. بیشترین واریته‌های جبری مطالعه شده خم‌های جبری صفحه‌اند که شامل خطوط، دایرهها، سهمیها، بیضیها، هذلولیها، خم‌های مکعبی مثل خم‌های بیضوی و خم‌های درجه چهار مثل lemniscateها و Cassini ovalها می‌باشند. یک نقطه از صفحه به خم بیضوی متعلق است اگر مختصات آن در یک معادلهٔ چند جمله‌ای داده‌شده صدق کند. سوالات بنیادی مربوط به مطالعهٔ نقاط خاصی مثل نقاط تکین، نقاط عطف و نقاط در بی‌نهایت می‌باشد. سوالات پیشرفته‌تر مرتبط می‌شوند به توپولوژی خم و معادلات بین خم‌های داده شده به‌وسیله معادلات مختلف.

نقش و کاربرد

هندسه جبری نقش محوری در ریاضیات مدرن ایفا کرده و پیوندهای مفهومی چندگانه‌ای با شاخه‌های گسترده‌ای از ریاضیات چون آنالیز مختلط، توپولوژی و نظریه اعداد دارد. در ابتدا مطالعهٔ دستگاه معادلات چند جمله‌ایهای چند متغیره موضوع هندسه جبری بود، آنجا که حل معادله از نظر خارج شده و فهمیدن خواص ذاتی جواب دستگاه معادلات اهمیت بیشتری پیدا می‌کند، آنجاست که هندسه جبری ظاهر می‌شود؛ چرا که در این مرحله دیگر یک جواب خاص اهمیت چندانی در مقابل آن خواص ندارد، این ما را به برخی قلمروها می‌کشاند که برخی از آن‌ها جزو عمیق‌ترین قلمروهای ریاضی هستند، چه از نظر مفهومی یا تکنیکی.

در قرن بیستم

در قرن بیستم، هندسه جبری به چندین زیرمجموعه تقسیم‌بندی شدند:

• جریان اصلی هندسه جبری به مطالعه نقاط مختلط واریته‌های جبری و به‌طور عمومی‌تر نقاطی که مختصات آن‌ها در میدان بسته جبری قرار دارند می‌پردازد.
• هندسه جبری حقیقی به مطالعه نقاط حقیقی یک واریته جبری می‌پردازد.
• هندسه سیاله‌ای و به‌طور عمومی‌تر هندسهٔ حساب به مطالعهٔ نقاط یک واریته جبری که مختصاتشان در میدان‌های غیر بسته قرار دارند می‌پردازد، مثل میدان‌هایی که در نظریه جبری اعداد بحث می‌شوند چون اعداد گویا، میدان‌های عددی، میدان‌های متناهی، میدان توابع و میدان p-adicها.
• بخش عمده نظریه تکینگی به تکینگی‌های واریته‌های جبری می‌پردازد.
• هندسه جبری محاسباتی قلمرویی است که با ظهور رایانهها از برخورد هندسه جبری و جبر رایانه‌ای به‌وجود آمده‌است. این قلمرو عمدتاً شامل طراحی الگوریتم و توسعه نرم‌افزار برای مطالعه خواص بارز یک واریته داده شده می‌باشد.

بسیاری از پیشرفت‌های جریان اصلی هندسه جبری در قرن بیستم در چارچوب جبر مجرد، صورت گرفت، با افزایش تأکید بر روی خواص «ذاتی» واریته‌های جبری که وابسته به هیچ‌کدام از روش‌های متفاوت جاسازی آن واریته در فضای مختصاتی اطرافیش (ambient) وابسته نباشد؛ این هدف موازی با پیشرفت در شاخه‌هایی چون توپولوژی، هندسه دیفرانسیل و هندسه مختلط می‌باشد. یکی از دستاوردهای کلیدی این هندسه جبری مجرد، نظریه اسکیم گروتندیک است که اجازه استفاده از نظریه شیف‌ها برای مطالعهٔ واریته‌های جبری را داده به طوری که این نحوه استفاده، شباهت بسیاری به استفاده از آن در مطالعه منیفلدهای دیفرانسیل و تحلیلی دارد. این دستاورد با توسعهٔ مفهوم نقطه به‌وجود آمد؛ در هندسه جبری کلاسیک، یک نقطه از واریته آفین را از طریق قضیه صفرهای هیلبرت می‌توان شناسایی کرد، به‌وسیله یک ایده‌آل ماکسیمال حلقه مختصاتی، در حالی که نقطه متناظر با آن در اسکیم آفین، همگی ایده‌آل‌های اولی از این حلقه می‌باشند. این بدین معناست که یک نقطه از چنین اسکیمی می‌تواند یا یک نقطه عادی، یا یک زیرواریته باشد. همچنین این رویکرد موجب اتحاد زبان و ابزارهای هندسه جبری کلاسیک گشته که به‌طور عمده با نقاط مختلط، و نظریه جبری اعداد مرتبط می‌گردد. اثبات وایلز بر حدس فرما به نام قضیه آخر فرما که به مدت طولانی، حل‌ناشدنی باقی مانده بود، اثباتی بر قدرت این رویکرد می‌باشد.

مفاهیم پایه ای

صفرهای همزمان چند جمله ای‌ها

کره و دایرهٔ اریب

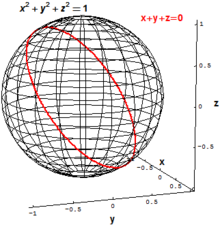
در هندسه جبری کلاسیک، علاقه اصلی بر روی اشیایی بود که به‌طور هم‌زمان مجموعه‌ای از چند جمله‌ای‌ها را ناپدید می‌کنند (صفر می‌کنند)، یعنی مجموعه نقاطی که هم‌زمان در یک یا تعداد بیشتری از معادلات چندجمله‌ای صدق می‌کنند. به عنوان مثال، کره دوبُعدی با شعاع ۱ در فضای اقلیدسی $\mathbb {R^{3}}$ را می‌توان به صورت مجموعه تمام نقاط (x,y,z)ی تعریف کرد که در این معادله، صدق می‌کنند:

$x^{2}+y^{2}+z^{2}-1=0.\,$

یک دایرهٔ «اریب» در $\mathbb {R^{3}}$ را می‌توان به صورت مجموعه نقاط (x,y,z) تعریف کرد که در دو معادلهٔ چندجمله‌ای زیر، هم‌زمان، صدق می‌کنند:

$x^{2}+y^{2}+z^{2}-1=0,\,$

$x+y+z=0.\,$

واریته‌های آفین

مقاله اصلی: واریته‌های آفین

ابتدا با یک میدان $\mathrm {k}$ شروع می‌کنیم. در هندسه جبری کلاسیک، این میدان، همیشه میدان اعداد مختلط $\mathbb {C}$ بود؛ اما بسیاری از نتایج با فرض یک میدان جبره بستی چون $\mathrm {k}$ هم، معتبر باقی خواهند ماند. ما فضای آفین $\mathrm {n}$ بعدی روی $\mathrm {k}$ را در نظر گرفته و آن را با $\mathbb {A^{n}(k)}$ نمایش می‌دهیم (یا صرفاً با $\mathbb {A^{n}}$، هنگامی که $\mathrm {k}$ در متن واضح باشد). هنگامی که دستگاه مختصات ثابت و مشخص باشد، می‌توان $\mathbb {A^{n}}$ را با $k^{n}$ یکی گرفت. هدف کار نکردن با $k^{n}$ این است که ساختار فضای برداری که $k^{n}$ با خود حمل می‌کند «فراموش» شود.

یک تابع $f:\mathbb {A} ^{n}\rightarrow \mathbb {A} ^{1}$ را چندجمله‌ای (یا منظم) گویند اگر آن را بتوان به صورت چندجمله‌ای نوشت، یعنی اگر وجود داشته باشد چندجمله‌ای چون $p$ در $k[x_{1},...,x_{n}]$ به گونه‌ای که برای هر نقطه $M$ با مختصات $(t_{1},...,t_{n})$ در $M$ داشته باشیم $f(M)=p(t_{1},...,t_{n})$.

هنگامی که یک دستگاه مختصات، انتخاب شد، توابع منظمِ روی n-فضای آفین را می‌توان با حلقه توابع چندجمله‌ای n متغیره روی $k$ یکی گرفت؛ به همین دلیل، مجموعه توابع منظم روی $k^{n}$ حلقه است و آن را با $k[\mathbb {A} ^{n}]$ نمایش می‌دهند.

یک چندجمله‌ای، در نقطه‌ای ناپدید می‌شود اگر که مقدارش در آن نقطه، صفر شود. فرض کنید $k^{n}$ مجموعه تمام چندجمله‌ای‌های درون $k[\mathbb {A} ^{n}]$ باشد. مجموعه ناپدیدشونده $S$ (یا مکان هندسی ناپدیدشونده یا مجموعه صفر) مجموعه $V(S)$ شامل تمام نقاط درون $\mathbb {A} ^{n}$ است که هر چندجمله‌ای $S$ بر روی آن، ناپدید می‌شوند؛ به‌طور نمادین:

$V(S)=\{(t_{1},\dots ,t_{n})\mid p(t_{1},\dots ,t_{n})=0{\text{ for all }}p\in S\}.\,$

برای مجموعه‌ای چون $S$، زیرمجموعه $V(S)$ از $\mathbb {A} ^{n}$ را مجموعه جبری می‌گویند. $V$ مخفف کلمه varietry است (یک نوع خاص از مجموعه‌های جبری که در ادامه، تعریف شده‌است).

فرض کنید که مجموعه‌ای مثل $U$ از $\mathbb {A} ^{n}$ داده شده باشد، آیا می‌توان مجموعه تمام چندجمله‌ای‌هایی که آن را تولید کرده‌اند را یافت؟ اگر $U$ زیرمجموعه دلخواهی از $\mathbb {A} ^{n}$ باشد، $I(U)$ را به این صورت تعریف کنید: مجموعه تمام چندجمله‌ای‌هایی که مجموعه صفرشان شامل $U$ باشد. $I$ اول کلمه ایدئال است: اگر دو چندجمله‌ای $f$ و $g$ هر دو روی $U$ ناپدید (صفر) شوند، آن‌گاه $f+g$ هم روی $U$ ناپدید می‌شود، و اگر $h$ یک چندجمله‌ای دلخواه باشد، آن‌گاه $hf$ هم روی $U$ ناپدید شده؛ به همین دلیل، $I(U)$ همیشه یک ایده‌آل از حلقه چندجمله‌ای‌های $k[\mathbb {A} ^{n}]$ است.

دو پرسش طبیعی، پیش می‌آید:

• برای یک زیرمجموعه دلخواه $U$ از $\mathbb {A} ^{n}$، چه زمان $U=V(I(U)$؟
• برای یک مجموعه دلخواه از چندجمله‌ای‌ها چون $S$، چه زمان $S=I(V(S))$؟

جواب سؤال اول با معرفی توپولوژی زاریسکی داده شد، یک توپولوژی روی $\mathbb {A} ^{n}$ که مجموعه‌های بسته آن، همان مجموعه‌های جبری هستند که به‌طور مستقیم ساختار جبری $k[\mathbb {A} ^{n}]$ را انعکاس می‌دهند. آن‌گاه $U=V(I(U))$ اگر و تنها اگر $U$ یک مجموعه جبری یا یک مجموعه بسته زاریسکی باشد. جواب سؤال دوم توسط قضیه صفرهای هیلبرت داده می‌شود. یکی از شکل‌های این قضیه می‌گوید که $I(V(S))$ رادیکال ایده‌آل‌های تولید شده توسط $S$ است. به بیان مجردتر، یک ارتباط گالوایی، وجود دارد که منجر به ظهور دو عملگر بستار می‌گردد؛ آن‌ها را می‌توان شناسایی کرده و به‌طور طبیعی، نقش بنیادینی در این نظریه بازی می‌کنند؛ مثال مربوط در بحث مربوط به ارتباط گالوایی، تشریح شده‌است.

به دلایل مختلف، ممکن است همیشه نخواهیم با کل ایده‌آل مربوط به یک مجموعه جبری چون $U$ کار کنیم. قضیه بنیادی هیلبرت می‌گوید که ایده‌آل‌های درون $k[\mathbb {A} ^{n}]$ همیشه متناهی، تولید شده‌اند.

یک مجموعه جبری را تحویل‌ناپذیر گویند اگر نتوان آن را به صورت اجتماع دو مجموعه جبری کوچک‌تر نوشت. هر مجموعه جبری به صورت اجتماع متناهی مجموعه‌های جبری تحویل‌ناپذیر بوده و این تجزیه یکتاست؛ لذا عناصر آن را مؤلفه‌های تحویل‌ناپذیر آن مجموعه جبری گویند. به یک مجموعه جبری تحویل‌ناپذیر واریته هم می‌گویند. مشخص می‌شود که یک مجموعه جبری واریته (مجموعه جبری تحویل‌ناپذیر) است اگر و تنها اگر به صورت مجموعه ناپدیدکننده (صفر کننده) یک ایده‌آل اول از حلقه چندجمله‌ای باشد.

برخی از مؤلفان، تمایز مشخصی بین مجموعه‌های جبری و واریته‌ها برقرار نمی‌کنند و در صورت لزوم از اصطلاح واریته تحویل‌ناپذیر برای ایجاد چنین تمایزی استفاده می‌کنند.

توابع منظم

مقاله اصلی: تابع منظم

درست همانگونه که توابع پیوسته نگاشت‌های طبیعی روی فضاهای توپولوژی و توابع هموار نگاشت‌های طبیعی روی منیفلدهای دیفرانسیل‌پذیر اند، دسته ای طبیعی از توابع روی یک مجموعه جبری نیز وجود دارند که به آن‌ها توابع منظم یا توابع چندجمله ای گویند. یک تابع منظم روی مجموعه ای جبری چون $V$ در $\mathbb {A} ^{n}$، تحدید توابع منظم روی $\mathbb {A} ^{n}$ به مجموعه جبری $V$ است. برای یک مجموعه جبری که روی میدان اعداد مختلط تعریف شده باشد، توابع منظم هموار و حتی تحلیلی اند.

ممکن است الزام توسعه پذیر بودن یک تابع منظم به کل فضای پیرامونی (ambient) به‌طور غیرطبیعی محدود کننده به نظر آید، اما این کار شباهت بسیاری به شرایط فضای توپولوژیکی نرمال دارد که در آن قضیه توسعه تیتز تضمین می‌کند که یک تابع پیوسته روی یک مجموعه بسته همیشه به فضای توپولوژیکی پیرامونی توسعه یابد.

توابع منظم روی $V$، درست همانند توابع منظم روی فضای آفینی، تشکیل یک حلقه می‌دهند که با $K[V]$ نمایش داده می‌شود. این حلقه را حلقه مختصاتی روی $V$ می‌نامند.

از آنجا که توابع منظم روی $V$ از توابع منظم روی $\mathbb {A} ^{n}$ نشأت می‌گیرند، رابطه ای بین حلقه‌های مختصاتیشان وجود دارد. به‌خصوص، اگر یک تابع منظم روی V تحدید دو تابع $f$ و $g$ در $K[\mathbb {A} ^{n}]$ باشد، آنگاه $f-g$ هم یک تابع چند جمله ای خواهد بود که روی $V$ ناپدید شده و لذا به $I(V)$ تعلق خواهد داشت. ازین‌رو، $K[V]$ را می‌توان با $K[\mathbb {A} ^{n}]/I(V)$ یکی گرفت.

هندسه جبری محاسباتی

می توان تاریخ پیدایش هندسه جبری محاسباتی را به نشست EUROSAM'79 (سمپوزیوم بین المللی در مورد دستکاری نمادین و جبری) که در مارسی، فرانسه در ژوئن 1979 برگزار شد، دانست. دنیس اس. آرنون نشان داد که تجزیه جبری استوانه ای جورج کالینز (CAD) امکان محاسبه توپولوژی مجموعه های نیمه جبری را فراهم می کند. برونو بوخبرگر پایه های گروبنر و الگوریتم خود را برای محاسبه آنها ارائه کرد. دانیل لازارد الگوریتم جدیدی را برای حل سیستم‌های معادلات چند جمله‌ای همگن با پیچیدگی محاسباتی ارائه کرد که اساساً در تعداد راه‌حل‌های مورد انتظار چند جمله‌ای است و بنابراین به سادگی در تعداد مجهولات نمایی است. این الگوریتم به شدت با برآیند چند متغیره مکالی مرتبط است. از آن زمان، اکثر نتایج در این زمینه به یک یا چند مورد از این موارد یا با استفاده یا بهبود یکی از این الگوریتم‌ها و یا با یافتن الگوریتم‌هایی که پیچیدگی آنها صرفاً در تعداد متغیرها تصاعدی است، مربوط می‌شود. مجموعه‌ای از نظریه‌های ریاضی مکمل روش‌های نمادین به نام هندسه جبری عددی در چند دهه گذشته توسعه یافته است. روش محاسباتی اصلی، ادامه هموتوپی است. برای مثال، این مدل از محاسبات ممیز شناور برای حل مسائل هندسه جبری پشتیبانی می کند.

بر اساس گروبنر

مبنای گروبنر سیستمی از مولدهای یک ایده آل چند جمله ای است که محاسبه آن امکان کسر بسیاری از ویژگی های تنوع جبری وابسته را که با ایده آل تعریف می شود را فراهم می کند. با توجه به یک ایده آل I که مجموعه جبری V را تعریف می کند: V خالی است (بیش از یک پسوند جبری بسته از فیلد پایه)، اگر و فقط در صورتی که مبنای گروبنر برای هر ترتیب تک جمله ای به {1} کاهش یابد. با استفاده از سری هیلبرت می توان بعد و درجه V را از هر مبنای گروبنر از I برای یک مرتبه یکپارچه محاسبه کرد که درجه کل را اصلاح می کند. اگر بعد V 0 باشد، می توان نقاط (تعداد محدود) V را از هر مبنای گروبنر I محاسبه کرد (به سیستم معادلات چند جمله ای مراجعه کنید). یک محاسبات مبتنی بر گروبنر به شخص اجازه می دهد تا تمام اجزای تقلیل ناپذیر موجود در یک ابرسطح معین را از V حذف کند. یک محاسبات مبتنی بر گروبنر به فرد اجازه می دهد تا بسته شدن Zariski تصویر V را با طرح ریزی روی مختصات اولیه k، و زیر مجموعه ای از تصویر که در آن طرح ریزی مناسب نیست، محاسبه کند. به طور کلی تر، محاسبات مبتنی بر گروبنر به فرد اجازه می دهد تا بسته شدن Zariski تصویر و نقاط بحرانی یک تابع منطقی V را در یک نوع وابسته دیگر محاسبه کند. محاسبات مبتنی بر گروبنر به شخص اجازه نمی دهد که تجزیه اولیه I یا ایده آل های اولیه را که مؤلفه های تقلیل ناپذیر V را تعریف می کنند، مستقیماً محاسبه کند، اما اکثر الگوریتم ها برای این کار شامل محاسبات پایه گروبنر هستند. الگوریتم‌هایی که مبتنی بر پایه‌های گروبنر نیستند از زنجیره‌های منظم استفاده می‌کنند، اما ممکن است در برخی شرایط استثنایی به پایه‌های گروبنر نیاز داشته باشند. محاسبه پایه های گروبنر دشوار است. در واقع، ممکن است در بدترین حالت، چند جمله‌ای داشته باشند که درجه آن‌ها از نظر تعداد متغیرها دوبرابر نمایی است و تعدادی چندجمله‌ای که نیز دو برابر نمایی است. با این حال، این تنها یک پیچیدگی در بدترین حالت است، و محدودیت پیچیدگی الگوریتم لازارد در سال 1979 ممکن است اغلب اعمال شود. الگوریتم Faugère F5 این پیچیدگی را درک می کند، زیرا ممکن است به عنوان بهبود الگوریتم لازارد در سال 1979 در نظر گرفته شود. نتیجه این است که بهترین پیاده‌سازی‌ها به فرد امکان می‌دهد تقریباً به‌طور معمول با مجموعه‌های جبری با درجه بیش از 100 محاسبه کند. این بدان معناست که در حال حاضر، دشواری محاسبه بر اساس گروبنر به شدت با دشواری ذاتی مسئله مرتبط است.

تجزیه جبری استوانه ای (CAD)

CAD الگوریتمی است که در سال 1973 توسط G. Collins برای پیاده سازی قضیه Tarski-Seidenberg در مورد حذف کمیت بر روی اعداد واقعی با پیچیدگی قابل قبولی معرفی شد. این قضیه به فرمول های منطق مرتبه اول مربوط می شود که فرمول های اتمی آن برابری های چند جمله ای یا نامساوی بین چندجمله ای ها با ضرایب واقعی است. بنابراین، این فرمول ها فرمول هایی هستند که ممکن است از فرمول های اتمی توسط عملگرهای منطقی و (∧)، یا (∨)، نه (¬)، برای همه (∀) و (∃) ساخته شوند. قضیه تارسکی بیان می کند که از روی چنین فرمولی می توان فرمول معادل را بدون کمیت (∀, ∃) محاسبه کرد. پیچیدگی CAD در تعداد متغیرها دو برابر است. این بدان معنی است که CAD در تئوری اجازه می دهد تا هر مسئله هندسه جبری واقعی را که ممکن است با چنین فرمولی بیان شود، حل کند، که تقریباً هر مشکلی در مورد انواع و مجموعه های نیمه جبری صریح داده شده است. در حالی که محاسبات مبتنی بر گروبنر فقط در موارد نادر دارای پیچیدگی نمایی مضاعف است، CAD تقریباً همیشه این پیچیدگی بالا را دارد. این به این معنی است که، مگر اینکه اکثر چند جمله ای های ظاهر شده در ورودی خطی باشند، ممکن است مشکلات بیش از چهار متغیر را حل نکند. از سال 1973، بیشتر تحقیقات در مورد این موضوع یا به بهبود CAD یا یافتن الگوریتم های جایگزین در موارد خاص مورد علاقه عمومی اختصاص یافته است. به عنوان نمونه ای از وضعیت هنر، الگوریتم های کارآمدی برای یافتن حداقل یک نقطه در هر جزء متصل از یک مجموعه نیمه جبری وجود دارد، و بنابراین برای آزمایش خالی بودن یک مجموعه نیمه جبری. از سوی دیگر، CAD هنوز در عمل بهترین الگوریتم برای شمارش تعداد اجزای متصل است.

=== پیچیدگی مجانبی در مقابل کارایی عملی === الگوریتم‌های عمومی اولیه هندسه محاسباتی دارای پیچیدگی دوگانه در بدترین حالت هستند. به طور دقیق تر، اگر d حداکثر درجه چند جمله ای های ورودی و n تعداد متغیرها باشد، پیچیدگی آنها حداکثر برای $d^{2^{cn}}$ است. مقداری ثابت c، و برای برخی از ورودی‌ها، پیچیدگی حداقل $d^{2^{c'n}}$ برای یک ثابت دیگر c است. در طول 20 سال آخر قرن بیستم، الگوریتم های مختلفی برای حل مسائل فرعی خاص با پیچیدگی بهتر معرفی شده اند. اکثر این الگوریتم‌ها دارای پیچیدگی $d^{O(n^{2})}$ هستند. در میان این الگوریتم‌ها که یک مشکل فرعی از مسائل حل شده توسط پایه‌های گروبنر را حل می‌کنند، می‌توان به «آزمایش در صورتی که یک تنوع وابسته خالی است» و «حل سیستم‌های چند جمله‌ای ناهمگن که تعداد راه‌حل‌های محدودی دارند» اشاره کرد. چنین الگوریتم‌هایی عبارتند از. به ندرت اجرا می شود، زیرا در بیشتر مدخل ها، الگوریتم های F4 و F5 Faugère کارایی عملی بهتری دارند و احتمالاً پیچیدگی مشابه یا بهتری دارند ("احتمالا" زیرا ارزیابی پیچیدگی الگوریتم های مبتنی بر گروبنر در یک کلاس خاص از ورودی ها کار دشواری است. که تنها در چند مورد خاص انجام شده است). الگوریتم های اصلی هندسه جبری واقعی که یک مسئله حل شده توسط CAD را حل می کند به توپولوژی مجموعه های نیمه جبری مربوط می شود. ممکن است «شمارش تعداد مؤلفه‌های متصل»، «آزمایش دو نقطه در یک مؤلفه» یا «محاسبه طبقه‌بندی ویتنی از یک مجموعه جبری واقعی» استناد شود. آنها دارای پیچیدگی $d^{O(n^{2})}$ هستند، اما ثابت درگیر نماد "O" به قدری زیاد است که استفاده از آنها برای حل هر مشکل غیر ضروری که به طور موثر توسط CAD حل می شود، غیر ممکن است حتی اگر بتوان از تمام توان محاسباتی موجود در جهان استفاده کرد. بنابراین، این الگوریتم‌ها هرگز پیاده‌سازی نشده‌اند و این یک حوزه تحقیقاتی فعال برای جستجوی الگوریتم‌هایی است که در کنار هم از پیچیدگی مجانبی خوب و کارایی عملی خوبی برخوردار هستند.

منابع

https://en.m.wikipedia.org/wiki/Algebraic_geometry#/editor/9

https://fa.m.wikipedia.org/wiki/هندسه_جبری#/languages

https://de.m.wikipedia.org/wiki/Algebraische_Geometrie