آشنایی با چندوجهیها/مشخصه اویلر
مشخصه اویلر كه با حرف يوناني خى () نشان داده مى شود مشخصه اى است كه در ابتدا براى چندوجهى ها و به شكل زير تعريف شد[۱]:
که E، V و F بهترتیب تعداد رأسها، اضلاع و وجههای چندوجهی هستند.
تاريخچه
[ویرایش]مشخصهٔ اویلر، در آغاز برای چندوجهیها تعریف شده و برای اثبات قضیههای مختلفی در مورد چندوجهیها و تقسیمبندی اجسام افلاطونی به کار رفت. لئونارد اویلر که این پارامتر به نام اوست، عمدهٔ این کارهای اولیه را انجام داد. بعدها در ریاضیات مدرن، این مفهوم در همولوژی کاربرد پیدا کرد.
چندوجهى محدب
[ویرایش]مشخصه اويلر هر چندوجهى محدب همواره ٢ و به شرح زير است:
كه با نام قضیهٔ چندوجهی اویلر نيز شناخته مى شود.جدول زير بررسى مشخصه اويلر را در تعدادى از چندوجهى هاى محدب نشان مى دهد:

| نام | تصوير | رأسها V |
اضلاع E |
وجهها F |
مشخصهٔ اویلر: V − E + F |
|---|---|---|---|---|---|
| چهاروجهی | 
|
۴ | ۶ | ۴ | ۲ |
| مکعب | 
|
۸ | ۱۲ | ۶ | ۲ |
| هشتوجهی | 
|
۶ | ۱۲ | ۸ | ۲ |
| دوازدهوجهی | ۲۰ | ۳۰ | ۱۲ | ۲ | |
| بیستوجهی | 
|
۱۲ | ۳۰ | ۲۰ | ۲ |
چندوجهى مقعر
[ویرایش]برحلات چندوجهى هاى محدب، چندوجهى هاى مقعر مى توانند مشخصه هاى اويلر گوناگونى داشته باشند كه در جدول زير نشان داده شده:
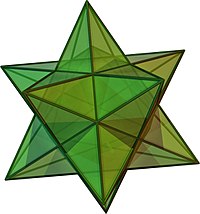
| تصوير | رأسها V |
اضلاع E |
وجهها F |
مشخصهٔ اویلر: V − E + F |
|---|---|---|---|---|

|
۶ | ۱۲ | ۷ | ۱ |

|
۱۲ | ۲۴ | ۱۲ | ۰ |

|
۱۲ | ۲۴ | ۱۰ | −۲ |

|
۱۲ | ۳۰ | ۲۰ | ۲ |
اثبات قضیهٔ چندوجهی اویلر
[ویرایش]
دلایل زیادی بر فرمول اولر وجود دارد. به شرح زیر یکی از آنها توسط کوشی داده شده است. این مورد برای هر چند وجهی محدب و به طور کلی برای هر چند وجهی که مرزش از نظر توپولوژیکی معادل کره است و وجوه آن از نظر توپولوژیکی برابر دیسک است ، اعمال می شود: یک وجه از سطح چند وجهی را بردارید. با کشیدن اضلاع وجه برداشته شده از یکدیگر ، بقیه را به یک نمودار مسطح از نقاط و منحنی ها تغییر شکل دهید ، به گونه ای که محیط وجه برداشته شده به صورت خارجی قرار گیرد ، گرافی که به دست آمده است ، همانطور که توسط اولین مورد از سه نمودار مخصوص مورد مکعب. (این فرض که سطح چندوجهی در ابتدا با کره هم شکل است ، این امر را امکان پذیر می کند.) پس از این تغییر شکل ، وجه های منتظم به طور کلی دیگر منتظم نیستند. تعداد رئوس و اضلاع ثابت مانده است ، اما تعداد وجوه يكى کاهش یافته است. بنابراین ، اثبات فرمول اویلر برای چند وجهی به اثبات V - E + F = 1 برای این جسم مسطح تغییر شکل داده می شود.
اگر یک وجه با بیش از سه ضلع وجود دارد ، یک مورب ترسیم کنید - یعنی یک منحنی از طریق وصل کنید که دو راس که هنوز به هم وصل نشده اند را بهم متصل کند. این یک ضلع و یک وجه را اضافه می کند و تعداد رئوس را تغییر نمی دهد ، بنابراین مقدار V - E + F را تغییر نمی دهد (فرض اینکه همه چهره ها دیسک هستند در اینجا لازم است ، تا از طریق قضیه منحنی اردن نشان دهیم که این با افزایش تعداد چهره ها یک به یک افزایش می یابد.) افزودن اضلاع ها را به این روش ادامه دهید تا همه سطوح مثلث شوند.
با حفظ این که مرز خارجی همیشه یک چرخه ساده است ، به طور مکرر از هر دو تغییر زیر استفاده کنید:
- مثلثی که فقط یک ضلع آن در مجاورت قسمت بیرونی است را بردارید ، همانطور که در نمودار دوم نشان داده شده است. این تعداد اضلاع و وجوه را هر یک به یک کاهش می دهد و تعداد رئوس را تغییر نمی دهد ، بنابراین V - E + F را حفظ می کند.
- مثلثی را که دو ضلع آن در قسمت خارجی شبکه مشترک است حذف کنید ، همانطور که در نمودار سوم نشان داده شده است. هر حذف مثلث یک راس ، دو ضلع و یک وجه را از بین می برد ، بنابراین V - E + F را حفظ می کند.
این تبدیلات در نهایت نمودار مسطح را به یک مثلث واحد تقلیل می دهند.در اين مرحله مثلث داراى ٣ ضلع، ٣ رأس و ١ سطح است. بنابرين ١=V - E + F مى شود و از آنجا كه در ابتدا ١ وجه را حذف كرديم، براى چندوجهى مشخصه اويلر برابر با ٢=١+١ مى شود. [۲]
منابع
[ویرایش]- ↑ «Euler Characteristic». MathWorld. بازبینیشده در ۱۲ آوریل ۲۰۱۴.
- ↑ Eppstein, David. "Twenty Proofs of Euler's Formula: V-E+F=2". Retrieved 3 June 2013.



