هندسه مقدماتی

نسخه کنونی و قابل ویرایش این کتاب را می‌توانید در وبگاه ویکی‌کتاب در نشانی زیر بیابید
https://fa.wikibooks.org/wiki/%D9%87%D9%86%D8%AF%D8%B3%D9%87_%D9%85%D9%82%D8%AF%D9%85%D8%A7%D8%AA%DB%8C

شما اجازه کپی و پخش این اثر را تحت مجوز مستندات آزاد گنو دارید.

مقدمه

'

مقدمه

خط

هندسه مقدماتی

هندسه یکی از درس های بسیار شیرین ریاضی است و کاربردهای زیادی در زندگی دارد. اما متاسفانه تعریف های زیاد و البته پیچیده که هر کدام از مفاهیم دارد بچه ها را از این درس زیبا زده می کند. در این کتاب سعی بر آن کرده‌ایم که مفاهیم پایه هندسه را به زبانی ساده بیان شود، امیدواریم برایتان مفید باشد.

خط

'

خط

انواع خط

هندسه مقدماتی

خط دارای تعاریف مختلفی می باشد که در اینجا ما به دوتا از آن ها اشاره می کنم.

خط امتداد نقطه است.
بر اثر حرکت و امتداد یک نقطه بر صفحه در یک راستا خط شکل می گیرد.

انواع خط

خط

انواع خط

مریع

هندسه مقدماتی

خط داری انواع مختلفی می باشد که مهمترین آن ها عبارتند از:

نیم خط: خطی است که از یکسو نامتناهی (بی پایان) و از سوی دیگر محدود (متناهی) به یک نقطه باشد.
پاره‌خط: در هندسه به جزئی از خط گفته می‌شود که به دو نقطه انتهایی محدود شده، و تمامی نقاط مابین آن دو را در بر بگیرد.

مربع

انواع خط

مربع

مستطیل

هندسه مقدماتی

مربع یا چهارگوش در هندسه یک چهار ضلعی منتظم است به عبارت دیگر خمی بسته‌است که چهار ضلع دارد که همهٔ این ضلع‌ها با هم برابر اند و با یکدیگر دو به دو زاویهٔ ۹۰ درجه یا راست می‌سازند.

ساخت

پویانمایی روبرو چگونگی کشیدن یک مربع با کمک یک پرگار و ستاره (ریاضی) را نمایش می‌دهد.

پیرامون و سطح

مساحت یک مربع برابر است با حاصل ضرب طول ضلع‌های مجاورش

مستطیل

مربع

مستطیل

دایره

هندسه مقدماتی

در هندسه اقلیدسی، مستطیل چهارضلعی است که تمام زوایای آن قائمه باشند. مستطیل نوعی متوازی الاضلاع است که هر دو ضلع همسایه بر هم عمود هستند.

فرمول

دایره

مستطیل

دایره

مثلث

هندسه مقدماتی

دایره مکان هندسی نقاطی از صفحه است که فاصله‌شان از نقطه ی ثابتی واقع در آن صفحه، مقدار ثابتی باشد. نقطه ی ثابت مرکز دایره و مقدار ثابت اندازه ی شعاع دایره نامیده می‌شود.

مثلث

مُثَلَّث (سه‌گوش) یک چندضلعی با سه ضلع است. مثلث شکلی مسطح است که از اتصال سه نقطه غیرهم‌خط در صفحه به وجود می‌آید. مثلث دارای سه ضلع، سه زاویه، و سه رأس است.

مساحت مثلث

مساحت یک مثلث برابر یک دوم طول یک ضلع، ضرب در طول ارتفاع وارد بر آن، یعنی فاصله رأس سوم تا خط شامل ضلع انتخاب‌شده، است.

مساحت مثلث را از رابطه زیر به دست می‌آورند:

۲ ÷ ( قاعده × ارتــــــفاع ) = مساحت مثلث

محیط مثلث

محیط مثلث را از رابطه زیر به دست می‌آورند:

مجموع سه ضلع = محیط مثلث

لوزی

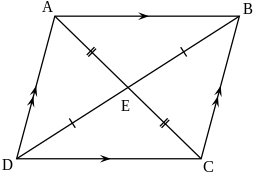
در هندسه، هر لوزی یک چهار ضلعی متساوی الاضلاع است. به بیان دیگر یک چند ضلعی با چهار ضلع، که اضلاعش با هم برابر هستند. در لوزی قطرها نیز عمود منصّف یکدیگرند. مجموع دو زاویه مجاور با هم در لوزی برابر ۱۸۰ درجه می باشد.

متوازی‌الأضلاع

در هندسه، متوازی‌الأضلاع به چهارضلعی گویند که اضلاع روبروی آن دو به دو با هم موازی باشند. اندازه اضلاع و زوایای روبرو در متوازی‌الأضلاع با هم برابر است.

بادبادک(هندسه)

در هندسهٔ اقلیدوسی یک بادبادک یک چهارضلعی محدب است که دو ضلع مجاور برابر داشته باشد. برخلاف متوازی‌الاضلاع که دو ضلع روبروی برابر دارد. این چهارضلعی مانند بادبادکی است که در آسمان پرواز می‌کند و به همین دلیل این چنین نام گذاری شده‌است.

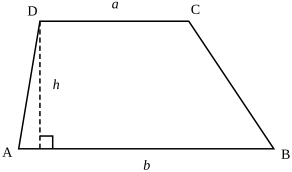
ذوزنقه

ذوزنقه، شکلی است چهارضلعی که فقط دو ضلع آن با هم موازی هستند.

در این شکل، زوایای مجاور به دو ضلع غیر موازی با هم مکمل اند.

شش‌ضلعی‌منتظم

شش‌ضلعی‌منتظم٬یک‌نوع چندضلعی‌منتظم است که دارای شش ضلع و زاویه برابر است. زاویه داخلی شش‌ضلعی‌منتظم دو برابر زاویه خارجی آن است. اگر شش‌ضلعی‌منتظم در دایره محاط‌شود، ۶ کمان مساوی که مجموع ام برابر با°۳۶۰ درجه می‌شود ایجاد‌ می‌کند.

محیط و مساحت

محیط

محیط ‌چندضلعی‌منتظم همیشه بر اساس این‌رابطه نوشته می‌گردد.

${P=an}$

a=اندازه ضلع چندضلعی

n=تعداد اضلاع چندضلعی

محیط شش‌ضلعی‌منتظم بر اساس این رابطه نوشته می‌گردد

${P=6a}$

مساحت

مساحت یک شش‌ضلعی‌منتظم این‌گونه است که اگر به شش مثلث تقسیم کنیم، آن شش مثلث هم‌مساحت و هم‌اندازه هستند و هر شش مثلث مثلث متساوی‌الاضلاع است.

مساحت شش‌ضلعی‌منتظم بر اساس این رابطه نوشته می‌گردد

$A=1/5a^{2}{\sqrt {3}}$

مساحت شش ضلعی منتظم با فرمول مساحت چندضلعی هم بدست می آید که با فرمول فوق برابر است

$A={\tfrac {1}{4}}6a^{2}\cot {\frac {\pi }{6}}={\displaystyle 1.5a^{2}{\sqrt {3}}}$

مکعب

مُکَعَّب به حجم بسته سه بعدی گویند که از ۶ مربع برابر تشکیل شده باشد. به صورتی که هر ضلع هریک از مربعها با تنها یک مربع دیگر مشترک باشد و در راس‌ها سه مربع با یکدیگر در ارتباط هستند.

کره

کُره یک جسم هندسی کاملاً گرد در فضای سه بعدی است. برای نمونه توپ یک کره‌است. کره مانند یک دایره می‌باشد که در دو بعد است، در فضای سه بعدی یک کره کاملاً متقارن در گرداگرد یک نقطه‌است.

مخروط

مخروط یکی از گونه‌های هرم است که قاعدهٔ آن دایره است.

یک مخروط یک شکل هندسی سه‌بُعدی است که از پایهٔ تختش (سطح مقطع مخروط) به آرامی یا به سرعت (به سطح قاعده و ارتفاع بستگی دارد) تا راس باریک می‌شود.

بخش های مخروطی نام اشکالی است که ابتدا باید چند تعریف زیر را یاد گرفت :

صفحه مخروطی : دو پاره خط قاطع در فضا را در نظر بگیرید . حال اگر یک پاره خط از آن دو حول پاره خط دیگری در فضا دوران کند به طوری که اولی گردش کرده و دومی ثابت باشد,شکلی به نام صفحه مطروطی ایجاد می شود.

که به پاره خط دوران کرده مولد و به هر یک از مخروط های ایجاد شده یک دامنه گویند.

مقاطع مخروطی

با توجه به تعریف بالا اگر یک صفحه و یک صفحه مخروطی را در نظر داشته باشید از برخورد این دو در فضا تنها هفت شکل زیر پدید می آید:

نقطه
یک خط راست
دو خط متقاطع
دایره
بیضی
سهمی
هذلولی

هرم

هرم شکلی سه‌بعدی است که از اتصال نقطه‌ای در فضا به بتمام نقاط شکلی بسته در صفحه به وجود می‌آید. به آن نقطه، رأس هرم و به آن شکل مسطح، قاعده هرم گفته می‌شود.

ساختمان هرمی دانشگاه ایالتی کالیفرنیا در لانگ بیچ

استوانه

اُستوانه یکی از پایه‌ای ترین شکل‌های منحنی فضایی در هندسه است که سطح دور آن را مجموعه نقاطی تشکیل می‌دهد که در فاصلهٔ یکسان از یک خط راست قرار دارند، این خط راست محور نام دارد.

نقطه (هندسه)

نقطه یا نقطه فضایی در هندسه، توپولوژی و دیگر شاخه‌های ریاضیات، مفهومی است مجرد برای بیان موقعیتی دقیق در مکان. به بیانی ساده‌تر، نقطه وجود خارجی ندارد و تنها یک مفهوم است. نقطه‌ها در هندسه بدون بُعد هستند، پس هیچ‌یک از پارامترهای اندازه‌گیری بُعد همچون طول، مساحت و حجم را ندارند.

عمود

در هندسه مقدماتی، واژهٔ عمود رابطهٔ دو خط را توصیف می‌کند که با زاویه قائمه با یکدیگر تقاطع می‌کنند. یعنی زمانی گفته می‌شود یک خط بر یک خط دیگر عمود است که آن دو خط با یکدیگر زاویه قائمه بسازند.

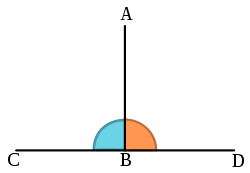
خط AB بر خط CD عمود است، زیرا دو زاویه‌ای که ایجاد می‌کند (که با رنگ نارنجی و آبی نشان داده شده‌اند) هر دو زاویه قائمه هستند.

موازی

در هندسه، خطوط موازی، خطوطی در یک صفحه هستند که یکدیگر را قطع نمی‌کنند. ویژگی‌های خطوط موازی، پایهٔ اصل توازی اقلیدسی را تشکیل می‌دهند.

صفحه

در ریاضیات به یک سطح هموار دوبعدی، صفحه می‌گویند. گویی یک صفحه نمایش دو بعدی از یک نقطه (صفر بُعد)، یک خط (یک بعد) و یک فضا (سه بعد) است.

طول

طول یا درازا کمیتی است برای اندازه‌گیری فاصله ی دو نقطه در فضا به کار می رود.

مساحت و حجم

حجم و مساحت،دو اصول مهم در علم ریاضیات و هندسه و به خصوص در هندسه فضایی است،دوران،مقطع،برش،رسم سه نما،محاط و... از مهم ترین موارد حجم و مساحت است.

تعریف حجم و مساحت

حجم:به مقدار فضایی که یک جسم اشغال می‌کند حجم می‌گویند. واحد حجم برابر با واحد مکعب است.حَجم کمیتی از فضای سه‌بعدی است که با یک مرز مشخص محدود شده‌است برای نمونه فضای اشغالی یک ماده (جامد، گاز، مایع، پلاسما) یا شکل آن است.

مساحت:نوعی کمیت است که مقدار سطح رویه اجسام سه بعدی و مقدار درونی اجسام دوبعدی را محاسبه می‌کند واحد مساحت برابر با واحدمربع است.مساحت کمیتی است که وسعت یک ناحیه را روی صفحه یا روی یک سطح منحنی بیان می کند.

تعریف احجام هندسی

حجم های هندسی به اجسام هایی گفته می‌شود که برای آنها می‌توانیم برای آنهافرمول سطح و حجم بنویسیم.حجم آن اجسام هندسی را می‌توانیم به روش الگویابی با استفاده از تجزیه و تحلیل و اندازه گیری حجم اجزای متناظر و جمع بندی و فرمول بندی آن می‌توان فرمول حجم آن را بدست آورد.

مساحت و حجم اشکال هندسی

حجم مکعب: $V=a^{3}\;$

مساحت مکعب: $V=6a^{2}\;$

حجم چهار وجهی: ${\textstyle V={{\sqrt {2}} \over 12}a^{3}\,}$

مساحت چهاروجهی: $V={{\sqrt {3}}a^{2}\,}$

حجم هشت وجهی منتظم:

$V={\frac {2}{3}}a^{3}$

مساحت هشت وجهی منتظم:

$V={2a^{2}{\sqrt {3}}\,}$

حجم مکعب مستطیل: ${\textstyle {V=abc}}$

مساحت مکعب مستطیل: ${\textstyle A=2ab+2ac+2cb}$

حجم منشور: $V=Sh$

حجم منشور با قاعده چندضلعی: $V={\frac {n}{4}}ha^{2}\cot {\frac {\pi }{n}}$

مساحت منشور با قاعده چندضلعی: $A={\frac {n}{2}}a^{2}\cot {\frac {\pi }{n}}+nah$

حجم استوانه: ${\displaystyle V=\pi r^{2}h}$

مساحت منشور: $A=\ Ph+2S$

مساحت استوانه: $A=2\pi r(r+h)\,\!$

حجم هرم: $V={\displaystyle {\frac {1}{3}}Sh}$

حجم مخروط: $V={\frac {1}{3}}\pi r^{2}h$

مساحت هرم: $B+{\frac {PL}{2}}\,\!$

مساحت مخروط: $\pi r(r+l)\,\!$

حجم کره: $V={\frac {4}{3}}\pi r^{3}$

مساحت کره: $4\pi r^{2}\ {\text{or}}\ \pi d^{2}\,\!$

حجم کره بیضی گون با قاعده دایره(کره گون): ${4 \over 3}\pi r^{2}h$

حجم کره بیضی گون مختلف: ${4 \over 3}\pi abc$

رأس

در هندسه، به نقطه‌ای که دو پهلوی مستقیم از یک چندضلعی باز یا بسته به هم می‌رسند رأس گفته می‌شود.

زاویه

زاویه یا گوشه یکی از مفاهیم هندسه است و به ناحیه‌ای از صفحه گفته می‌شود که بین دو نیم‌خط که سر مشترک دارند محصور شده‌است. به سر مشترک این دو نیم‌خط راس زاویه یا گوشه می‌گویند.

نگارخانه

نقاله برای کشیدن زاویه، داخل شابلون

هم‌نهشتی

در هندسه دو شکل هم‌نهشت هستند اگر هم شکل و هم‌اندازه باشند.

تشابه

هنگامی دو شکل هندسی متشابه هستند که هم‌شکل باشند.

نگارخانه

چندضلعی

در هندسه، چندضلعی به شکلی دوبعدی در صفحه گفته می‌شود که با مسیری بسته شامل تعداد متناهی خطوط راست محیط شده باشد. در فضای سه بعدی به آن چندوجهی گویند.

وتر

وتر بلندترین ضلع در مثلث قائم‌الزاویه است.

و رابطه آن بدین صورت است:(مربع طول وتر = مجموع مربع طول دو ضلع دیگر)

قضیه فیثاغورس

قضیهٔ فیثاغورس در هندسه و فضای اقلیدسی بخشی از صورت کلی قانونی می باشد که هنگامی که زاویهٔ بین دو بردار ۹۰ درجه‌است می‌باشد.به سخن دیگر در یک مثلث راست‌گوشه (قائم الزاویه) همواره مجموع توان‌های دوم دو ضلع برابر با توان دوم وتر است.

فرمول: $a^{2}+b^{2}=c^{2}$

اثبات با استفاده از بازچینی

پویانمایی برای نمایش یک اثبات دیگر بوسیلهٔ بازچینی

قطر

قطر یا ترامون در هندسه پاره‌خطی‌ست که هر دو رأس غیر مجاور یک چندضلعی یا چندوجهی را به هم متصل کند.

تقارن

تقارن یا همامونی به معنای تشابه بخش‌ها حول محور یا مرکز تقارن است.

نگارخانه

منحنی

در ریاضیات، مفهوم خم برای نشان دادن یک شیء یک بعدی و پیوسته به کار می‌رود. یک مثال ساده دایره‌است. در گفتگوی روزمره یک خط صاف خم در نظر گرفته نمی‌شود. ولی در مکالمهٔ ریاضیاتی خط‌های مستقیم و پاره خط‌ها نیز خم‌اند. تعداد زیاد دیگری خم در هندسه مطالعه می‌شوند.

محیط

محیط به معنای فراگیرنده است و به درازای بخش بیرونی یک شکل گفته می‌شود. یعنی فاصله‌ای که بر لبه بیرونی یک شکل می‌پیماییم تا به نقطه اول خود بازگردیم محیط می‌گوییم. به خود لبه بیرونی نیز اصطلاحاً محیط گفته می‌شود.

فرمول‌ها

شکل	فرمول	متغیرها
دایره	$2\pi r\,$	که در آن $r$ شعاع است.
مثلث	$a+b+c\,$	که در آن $b$ ، $a$ و $c$ طول پهلوهای مثلث هستند
چندضلعی متساوی‌الاضلاع	$n\times a\,$	که در آن $n$ تعداد پهلوها و $a$ طول یکی از پهلوها است.
چندضلعی منتظم	$2nb\sin({\frac {\pi }{n}})$	که در آن $n$ تعداد پهلوها و $b$ فاصله میان مرکز چندضلعی و یکی از رأس‌های چندضلعی است
چندضلعی کلی	$a_{1}+a_{2}+a_{3}+\ldots +a_{n}=\sum _{i=1}^{n}a_{i}$	که در آن $a_{i}$ طول $i$ اُمین (اولین، دومین، سومین ...، nامین) پهلو از یک چندضلعی n-پهلو است.

زاویه قائمه

خط جدا کنندهٔ AB که خط CD را قطع کرده‌است بر روی آن یک زاویهٔ راست یا ۹۰ درجه تشکیل داده‌است.

در هندسه و مثلثات یک زاویهٔ راست یا قائمه یا راست‌گوشه زاویه‌ای است که زاویهٔ تشکیل شده بوسیلهٔ دو نیمهٔ خط راست را نیمساز می‌کند (آن را به دو قسمت مساوی تقسیم می‌کند). بیان دقیق تر آن چنین است: اگر یک نیم‌خط به گونه‌ای باشد که نقطهٔ یک انتهای آن بر روی یک خط راست قرار داشته باشد و زاویه‌های مجاور آن با هم برابر باشد، آنگاه می‌توان گفت که این زاویه‌ها زاویهٔ راست اند.

انواع زاویه

زاویه‌ها را با توجه به مقدارشان به این صورت طبقه بندی می‌کنند:

۱- زاویه تند: زاویه را تند یا حاده می‌گوییم هرگاه اندازه اش کمتر از ۹۰ در جه باشد.

۲- زاویه راست: زاویه را راست یا قائم می‌گوییم هرگاه اندازه آن برابر ۹۰ در جه باشد.

۳- زاویه باز: زاویه را باز یا منفرجه می‌گوییم هرگاه بزرگتر از ۹۰ درجه و کمتر از ۱۸۰ درجه باشد.

۴- زاویه نیم صفحه: زاویه را نیم صفحه می‌گوییم هرگاه برابر ۱۸۰ درجه باشد.

۵- زاویه بازتاب: زاویه را زاویه بازتاب می‌گوییم هرگاه بزرگتر از ۱۸۰ درجه و کمتر از ۳۶۰ درجه باشد.

۶- زاویه کامل: زاویه را کامل یا تمام صفحه می‌گوییم هرگاه برابر ۳۶۰ درجه باشد.

هندسه اقلیدسی

هندسهٔ اقلیدسی به مجموعهٔ گزاره‌هایِ هندسی‌ای اطلاق می‌شود که به بررسی موجودات ریاضیاتی مثل نقطه و خط می‌پردازد و بر پایه‌هائی که اقلیدس ریاضی‌دان یونانی در کتاب خود به‌نام اصول عرضه کرده، بنا شده‌است.

نگارخانه

هندسه نااقلیدسی

هندسه‌های نااقلیدسی از مطالعهٔ عمیق‌تر موضوع توازی در هندسهٔ اقلیدسی پیدا شده‌اند. دو نیم‌خط موازی عمود بر پاره خط PQ را در نمودار شماره ۱ در نظر بگیرد. در هندسهٔ اقلیدسی فاصلهٔ (عمودی) بین دو نیم‌خط هنگامی که به سمت راست حرکت می‌کنیم فاصلهٔ p تا Q باقی می‌مانند.

نمودار شماره ۱ - تصویری از سه حالت اصلی در بحث هندسه‌های نااقلیدسی.

هندسه تحلیلی

هندسه تحلیلی شاخه‌ای از ریاضیات است که از ترکیب هندسه و جبر مقدماتی به وجود آمده‌است. در این رشته اشکال هندسی و روابط بین آن‌ها را با مقادیر و معادلات عددی و جبری بیان می‌کنند.

هندسه ریمانی

هندسه ریمانی شاخه‌ای از هندسه دیفرانسیل است که بررسی خمینه‌های ریمانی می‌پردازد. یک خمینه ریمانی خمینه‌ای است که مجهز به یک متریک ریمانی می‌باشد یعنی یک ضرب داخلی در فضای مماس بر هر نقطه خمینه که به طور هموار تغییر می‌کند.

هندسه جبری

هندسه جبری شاخه‌ای از ریاضیات است که مفاهیم جبر مجرد، به ویژه جبر جابجایی، را با مسائل هندسه می‌آمیزد. این شاخه از ریاضیات مدرن با آنالیز مختلط، توپولوژی و نظریه اعداد در ارتباط تنگاتنگ است.

هندسه دیفرانسیل

هندسه‌ی دیفرانسیل زمینه‌ای از ریاضیات است که به بررسی ویژگی‌های خمینه‌ها می‌پردازد. خمینه‌ها که مفهوم تعمیم‌یافته از رویه‌ها در ابعاد بالاتر هستند، مهم‌ترین مفهوم مورد بحث هندسه دیفرانسیل هستند.

قضیه هندسه دیفرانسیل

هندسه دیفرانسیل به مفاهیم هندسی در حساب دیفراسیل و انتگرال است که مفهوم هایی در قضیه های هندسی مثل مقطع مخروطی،مساحت و حجم اشکال سه بعدی،مثلثات کروی،مختصات کروی،مختصات استوانه ای و... بر اساس انحنایی که دارد را بر روش انتگرالی و حساب دیفرانسیل حل و اثبات می گردد.

هندسه تصویری

هندسه تصویری شاخه ای از دانش هندسه است که به مطالعه خواص هندسی می پردازد که در تبدیل های تصویری ثابت می مانند.

بعد

بُعد در معنی عادی به یک اندازه یا پارامتر گفته می‌شود که برای تعریف ویژگی‌های یک جسم به آن نیازمندیم، برای نمونه درازا، پهنا، بلندا و ژرفنا. برای بیان این اندازه‌ها در فارسی از واژه‌های عربی طول، عرض، ارتفاع و عمق هم استفاده می‌شود.

فضای یک بعدی

در فیزیک و ریاضیات و در فضای اقلیدسی به دنباله‌ای از n عدد حقیقی یک نقطه در فضای n بعدی گفته می‌شود و هنگامی که n=۱ باشد این نقطه درفضای یک بعدی جای دارد.

سیستم مختصاتی

دو دستگاه مختصات مشهور برای یک بعد وجود دارد.

بردار
زاویه

فضای دوبعدی

در فیزیک و ریاضی و در فضای اقلیدسی به دنباله‌ای از n عدد حقیقی یک نقطه در فضای n بعدی گفته می‌شود و هنگامی که n=۲ باشد این نقطه در فضای دوبعدی جای دارد.

دستگاه مختصاتی

سه دستگاه مختصات برای دو بعد وجود دارد:

دستگاه مختصات دکارتی
دستگاه مختصات قطبی
دستگاه مختصات جغرافیایی

فضای سه‌بعدی

در ریاضیات فضای سه بعدی فضای برداری دارای سه بعد و یک مدل هندسی از جهان فیزیکی است که در آن زندگی می‌کنیم. ابعاد سه‌گانه معمولاً به نام طول، عرض، و عمق (یا ارتفاع) شناخته می‌شوند اگر چه این نامگذاری اختیاری است.

قضیه فضای سه بعدی

این بعد یکی از بعدهای پیشرفته به حساب می آید و در زمینه های بردارهای سه بعدی،اشکال هندسی و... بررسی می شود.مکعب،مکعب مستطیل،متوازی السطوح یکی از اشکال های هندسی هستند که ازطریق بردارهای سه بعدی رسم شده اند. فضای سه بعدی سه اصل در مختصات دارد.

طول
عرض
ارتفاع

فضای سه بعدی دیگر

مختصات استوانه‌ای

مختصات استوانه‌ای نوعی مختصات متعامد (عمود برهم) است که در آن یک نقطه، در فضا بر روی قاعدهٔ یک استوانه در نظر گرفته می‌شود. مکان آن نقطه بر اساس شعاع و ارتفاع استوانه (r و z) و زاویه‌ای که شعاع قاعده گذرنده از آن نقطه با محور x می‌سازد (θ)، بیان می‌شود. این دستگاه، در حالت دوبعدی، با حذف مختص z به مختصات قطبی تبدیل می‌شود. در فیزیک و به ویژه در مباحث الکترومغناطیس و مخابرات به جای r، θ، z به ترتیب از حروف ρ، φ، z استفاده می‌شود.

مختصات کروی

در ریاضیات مختصات کروی،برای فضای سه بعدی است که در آن موقعیت یک نقطه با سه عدد مشخص می شود: فاصله شعاعی آن نقطه از یک مبدأ ثابت، زاویه قطبی آن اندازه گیری شده از یک جهت اوج ثابت ، و زاویه متعامد برآمدگی متعامد آن بر روی صفحه مرجعی که از مبدا می گذرد و متعامد به نقطه اوج است، از یک جهت مرجع ثابت در آن صفحه اندازه گیری می شود. می توان آن را نسخه سه بعدی سیستم مختصات قطبی دید .

فاصله شعاعی را شعاع یا مختصات شعاعی نیز می نامند . زاویه قطبی را می توان زاویه همبستگی ، زاویه اوج ، زاویه معمولی یا زاویه شیب نامید .

استفاده از نمادها و ترتیب مختصات در منابع و رشته ها متفاوت است. این مقاله از کنوانسیون ISO که اغلب در فیزیک با آن مواجه می‌شود، استفاده می‌کند :فاصله شعاعی، زاویه قطبی و زاویه ازیموت را نشان می دهد. در بسیاری از کتاب های ریاضی،یافاصله شعاعی، زاویه ازیموتال و زاویه قطبی را نشان می‌دهد و معانی θ و φ را تغییر می‌دهد . قراردادهای دیگری نیز استفاده می شود، مانند r برای شعاع از محور z ، بنابراین باید دقت زیادی برای بررسی معنای نمادها انجام شود.

طبق قراردادهای سیستم های مختصات جغرافیایی ، موقعیت ها با طول و عرض جغرافیایی و ارتفاع (ارتفاع) اندازه گیری می شوند. تعدادی سیستم مختصات آسمانی بر اساس صفحات بنیادی مختلف و با اصطلاحات مختلف برای مختصات مختلف وجود دارد. سیستم های مختصات کروی مورد استفاده در ریاضیات معمولاً به جای درجه از رادیان استفاده می کنند و زاویه آزیموتال را در خلاف جهت عقربه های ساعت از محور x به محور y اندازه می گیرند نه در جهت عقربه های ساعت از شمال (0 درجه) به شرق (90 درجه) مانند سیستم مختصات افقی . . زاویه قطبی اغلب با زاویه جایگزین می شودزاویه ارتفاع از صفحه مرجع اندازه گیری می شود، به طوری که زاویه ارتفاع صفر در افق باشد.

سیستم مختصات کروی سیستم مختصات قطبی دو بعدی را تعمیم می دهد. همچنین می توان آن را به فضاهای با ابعاد بالاتر گسترش داد و سپس به عنوان یک سیستم مختصات ابرکره ای نامیده می شود .