نگاهی به ریاضیات پیشرفته/نسخه چاپی
این یک نسخه چاپی است از نگاهی به ریاضیات پیشرفته این پیغام و هیچ چیز اضافیای در چاپ نمیافتند اگر میانگیر را خالی کنید. |
نسخه کنونی و قابل ویرایش این کتاب را میتوانید در وبگاه ویکیکتاب در نشانی زیر بیابید
https://fa.wikibooks.org/wiki/%D9%86%DA%AF%D8%A7%D9%87%DB%8C_%D8%A8%D9%87_%D8%B1%DB%8C%D8%A7%D8%B6%DB%8C%D8%A7%D8%AA_%D9%BE%DB%8C%D8%B4%D8%B1%D9%81%D8%AA%D9%87
مقدمه
ریاضیات یکی از بهترین علم در جهان است که بعد از آن علوم طبیعی است.دراین کتاب به مبحثهای پیشرفته و پیچیده ریاضی میپردازیم. این علم سرآمد تمامی علم هاست و ریاضیات در فیزیک، شیمی، مهندسی، نجوم، معماری و... بسیار کاربردی است.
ریاضیات از دور سخت است ولی اگر نزدیکش بروی هیچ سخت نیست.
دراین کتاب به مباحثهای پیشرفته و پیچیده ریاضی میپردازیم. ما در این کتاب به مباحثی چون ریاضیات، حسابان، هندسه و آنالیز می پردازیم و مفاهیم مهم، شاخههای ریاضیات، زمینههای پژوهش و ... را بررسی میکنیم. این ایبوک هم نسخه چاپی هم دارد و به صورت مشارکت گروهی است.
تعریف ریاضیات
ریاضیات یا انگارش فن محاسبه اعداد بوده و نیز به مطالعهٔ مباحثی چون کمیت (نظریه اعداد)، ساختار (جبر)، فضا (هندسه)، و تغییرات (آنالیز ریاضیات) میپردازد. در حقیقت تعریفی جهانی که همه بر سر آن توافق داشته باشند برای ریاضیات وجود ندارد.
بیشتر فعالیت های ریاضی شامل کشف و اثبات ویژگی های اشیاء انتزاعی با استدلال محض است. این اشیاء یا انتزاعی از طبیعت هستند، مانند اعداد یا خطوط طبیعی ، یا - در ریاضیات مدرن - موجوداتی هستند که دارای ویژگیهای خاصی هستند که بدیهیات نامیده میشوند . یک برهان متشکل از مجموعه ای از کاربردهای برخی قوانین قیاسی برای نتایج شناخته شده از قبل، از جمله قضایای اثبات شده قبلی ، بدیهیات و (در صورت انتزاع از طبیعت) برخی ویژگی های اساسی است که به عنوان نقطه شروع واقعی نظریه مورد بررسی در نظر گرفته می شوند. نتیجه یک برهان را قضیه می گویند.
ریاضیات به طور گسترده ای در علم برای مدلسازی پدیده ها استفاده می شود. این امکان استخراج پیش بینی های کمی از قوانین تجربی را فراهم می کند. به عنوان مثال، حرکت سیارات را می توان با استفاده از قانون گرانش نیوتن همراه با محاسبات ریاضی به طور دقیق پیش بینی کرد. استقلال حقیقت ریاضی از هر آزمایشی دلالت بر این دارد که صحت چنین پیشبینیهایی تنها به کفایت مدل برای توصیف واقعیت بستگی دارد. پیشبینیهای نادرست مستلزم نیاز به بهبود یا تغییر مدلهای ریاضی است، نه اینکه ریاضیات در خود مدلها اشتباه است. برای مثال، تقدم حضیض عطارد را نمی توان با قانون گرانش نیوتن توضیح داد، اما به طور دقیق توسط قانون گرانش نیوتن توضیح داده می شود. نسبیت عام اینشتین _ این تایید تجربی نظریه انیشتین نشان می دهد که قانون گرانش نیوتن تنها یک تقریب است، هرچند در کاربردهای روزمره دقیق است.
ریاضیات در بسیاری از زمینهها از جمله علوم طبیعی ، مهندسی ، پزشکی ، مالی ، علوم کامپیوتر و علوم اجتماعی ضروری است . برخی از حوزه های ریاضیات، مانند آمار و تئوری بازی ها، در ارتباط نزدیک با کاربردهای آنها توسعه یافته اند و اغلب در زیر ریاضیات کاربردی گروه بندی می شوند . سایر حوزههای ریاضی مستقل از هر کاربرد توسعه مییابند (و بنابراین ریاضیات محض نامیده میشوند )، اما کاربردهای عملی اغلب بعداً کشف میشوند. یک مثال مناسب مسئله فاکتورسازی اعداد صحیح، که به اقلیدس برمیگردد، اما قبل از استفاده در سیستم رمزنگاری RSA (برای امنیت شبکههای کامپیوتری) کاربرد عملی نداشت.
از نظر تاریخی، مفهوم برهان و دقت ریاضی مرتبط با آن برای اولین بار در ریاضیات یونان ظاهر شد، به ویژه در عناصر اقلیدس. از آغاز، ریاضیات اساساً به هندسه ، و حساب (دستکاری اعداد و کسرهای طبیعی ) تقسیم شد تا اینکه در قرن 16 و 17، جبر و حساب بی نهایت کوچک به عنوان حوزهای جدید معرفی شدند. از آن زمان، تعامل بین نوآوری های ریاضی و اکتشافات علمی به رشد سریع ریاضیات منجر شده است. در پایان سده نوزدهم، بحران اساسی ریاضیات منجر به نظامبندی روش بدیهی شد. این به نوبه خود باعث افزایش چشمگیر تعداد حوزه های ریاضی و زمینه های کاربردی آنها شد. نمونه ای از این طبقه بندی موضوع ریاضیات است که بیش از شصت حوزه سطح اول ریاضیات را فهرست می کند.
تاریخ
[ویرایش]

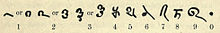
تاریخ ریاضیات را میتوان به عنوان دنبالهای از تجرید سازیهای فزاینده دید. اولین قابلیت تجرید سازی که در بسیاری از حیوانات مشترک است، احتمالاً مفهوم عدد است: فهم این مطلب که مجموعه دو سیب و مجموعه دو پرتقال (به عنوان مثال) با هم اشتراکی دارند، و آن کمیت تعدادشان است.
همانطور که شواهد بر روی چوبخط نشان میدهد، مردم پیشاتاریخ میتوانستند اشیاء فیزیکی را بشمرند و توانایی شمردن اشیاء تجریدی مثل روز، فصل و سال را نیز داشتند.
شواهد مربوط به ریاضیات پیچیدهتر تا ۳۰۰۰ قبل میلاد مشاهده نشده، زمانی که بابلیها و مصریها شروع به استفاده از حساب، جبر و هندسه برای محاسبات مربوط به مالیات و دیگر مفاهیم اقتصادی، و ساخت و ساز یا نجوم کردند. قدیمیترین متون ریاضیاتی مربوط به بینالنهرین و مصر میشود که به ۲۰۰۰–۱۸۰۰ قبل از میلاد بازمیگردد. بسیاری از متون اولیه سه تاییهای فیثاغوری را ذکر کرده و لذا به نظر میرسد که قضیه فیثاغورس[۵]
این قضیه بارها به روشهای مختلف هندسی و جبری اثبات شدهاست که برخی از این اثباتها به هزاران سال گذشته برمیگردند.</ref> کهنترین و گستردهترین توسعه ریاضیاتی بعد از حساب مقدماتی و هندسه باشد. در اسناد تاریخی، در ریاضیات بابلیها بود که حساب مقدماتی[۶] (جمع، تفریق، ضرب و تقسیم) ابتدا پدیدار گشت. بابلیها همچنین از یک دستگاه مکان-ارزشی بهره میجستند که در آن دستگاه اعداد پایه ۶۰[۷] پیادهسازی شده بود، ازین دستگاه عددی هنوز هم برای اندازهگیری زاویه[۸] و زمان استفاده میشود.
با آغاز سده ششم قبل از میلاد مسیح، ریاضیات یونانیها با فیثاغورسیها مطالعهٔ نظام مندی را در ریاضیات، به هدف شناخت بیشتر خود ریاضیات آغاز نمودند که سرآغاز ریاضیات یونانیها بود. حدود ۳۰۰ قبل از میلاد، اقلیدس روش اصول موضوعه ای را که هنوز هم در ریاضیات به کار میرود را معرفی کرد که شامل تعاریف، اصول، قضیه و اثبات بود. کتاب مرجع او که به اصول اقلیدس معروف است بهطور گسترده به عنوان موفقترین و تأثیر گذارترین کتاب مرجع همه زمانها شناخته میشود. بزرگترین ریاضیدانان باستان را اغلب ارشمیدس (۲۸۷ تا ۲۱۲ قبل از میلاد) اهل سیراکوز میدانند.او فرمولهایی برای محاسبهٔ مساحت و حجم اجسام در حال دوران پیدا کرد و از روش افنا برای محاسبه مساحت زیر منحنی سهمی با استفاده از جمع یک سری بینهایت استفاده کرد به گونه ای که بی شباهت با حساب دیفرانسیل و انتگرال مدرن نیست. دیگر دستاوردهای قابل توجه در ریاضیات یونان مقاطع مخروطی[۹] (آپولونیوس اهل پرگا، سده سوم قبل از میلاد)، مثلثات[۱۰] (هیپارکوس اهل نیکا (سده دوم قبل از میلاد))، و آغاز جبر (دیوفانتوس، سده سوم پس از میلاد) بود.
سیستم عددی هندو-عربی و قواعد استفاده از عملیاتش که امروزه در سراسر جهان استفاده میشود، در طی هزارهٔ اول میلادی در هند توسعه یافت و سپس از طریق ریاضیات اسلامی به جهان غرب انتقال یافت. دیگر پیشرفتهای مربوط به ریاضیات هندیها شامل تعریف مدرن سینوس[۱۱] و کسینوس[۱۲] و فرم اولیه سریهای بینهایتی است.

در طی عصر طلایی اسلام، که در سده نهم و دهم میلادی شکل گرفت، ریاضیات نوآوریهای مهمی را به خود دید که بر اساس ریاضیات یونانیها پایهریزی شده بود. مهمترین دستاوردهای ریاضیات اسلامی توسعهٔ جبر بود. دیگر دستاوردهای مهم ریاضیات دورهٔ اسلامی پیشرفت در مثلثات کروی[۱۳] و اضافه شدن اعشار[۱۴] به سیستم عددی عربی بود. بسیاری از ریاضیدانان این دوره فارسیزبان بودند مثل خوارزمی، خیام و شرف الدین توسی.
در طی اوایل عصر مدرن، ریاضیات شروع به توسعه شتابداری در غرب اروپا کرد. توسعه حساب دیفرانسیل و انتگرال توسط نیوتون و لایبنیز در سده هفدهم میلادی ریاضیات را متحول کرد. لئونارد اویلر مهمترین ریاضیدان سده هجدهم میلادی بود که چندین قضیه و کشفیات را به ریاضیات افزود. شاید مهمترین ریاضیدانان سده نوزدهم میلادی ریاضیدان آلمانی کارل فردریش گاوس بود که خدمات متعددی به شاخههای مختلف ریاضیات چون جبر، آنالیز، هندسه دیفرانسیل، نظریه ماتریس[۱۵]، نظریه اعداد[۱۶] و آمار[۱۷] کرد. در اوایل سده بیستم میلادی، کورت گودل، ریاضیات را با انتشار قضایای ناتمامیت خویش دچار تغییر کرد. این قضایا نشان دادند که هر سیستم اصول موضوعه سازگاری شامل گزارههای غیرقابل اثبات اند.
ریاضیات از آن زمان بهطور گستردهای توسعه یافتهاست و کنش و واکنشهای ثمربخشی بین ریاضیات و علوم ایجاد شده که به نفع هردو است. کشفیات ریاضیات تا به امروز نیز ادامه دارد. بر اساس نظر میخائیل سوریوک، که در ژانویه ۲۰۰۶ در بولتن انجمن ریاضی آمریکا منتشر شد، "تعداد مقالات و کتب پایگاه اطلاعاتی ژورنال Mathematical Review از سال ۱۹۴۰ (اولین سال عملیاتی شدن MR) اکنون به ۱٫۹ میلیون میرسد که سالانه بیش از ۷۵ هزار مورد به این پایگاه افزوده میشود. اکثریت کارهای گستردهای که در این اقیانوس وجود دارد شامل قضایای جدید ریاضیاتی و اثباتهایشان است.
چند اصطلاح مرتبط با ریاضیات
[ویرایش]- ریاضیات کاربردی[۱۸]
- ریاضیات محض[۱۹]
- علوم ریاضیات[۲۰]
یادداشت
[ویرایش]- ↑ پلیمپتون۳۲۲ نام یکی از معروفترین لوحهای رسی شامل ریاضیات بابلیان است. این لوح به خط میخی نوشته شده است و قدمتی بین ۱۹۰۰ تا ۱۶۰۰ ق.م. دارد. ۳۲۲ در نام این کتبیه از آن جهت آمده است که این لوح در مجموعه ج.ا. پلیمپتن در دانشگاه کلمبیا شماره ۳۲۲ را دارد.
- ↑ ارشمیدوس یک دانشمند،فیلسوف،ریاضیدان،هندسه دان، فیزیک دان،مخترع،ستاره شناس و مهندس یونانی است که در سال ۲۸۷ق.م در شهر سیراکوز و در سال۲۱۲ق.م در همان شهر در ۷۵سالگی از دنیا رفت. او در زمینه ریاضیات کارهای مهمی انجام داده است. او توانست مساحت و حجم استوانه،مخروط و کره را محاسبه کند و عدد پی را با دقت محاسبه کند و توانست نسبت حجم و مساحت کره را به حجم و مساحت استوانه بدست آورد و حتی او توانست نسبت V/S احجام را محاسبه کند.جایگاه وی در زمینه ریاضیات بالا است.
- ↑ روش اِفْنا،روشی برای یافتن مساحت یک شکل با محاط کردن دنبالهای از چندضلعیها در آن است به گونهای که مساحت آن چندضلعیها به سمت مساحت شکل مورد نظر همگرا شود. اگر دنباله به درستی ساخته شده باشد، با افزایش n، تفاضل مساحت چندضلعی nام و شکل مورد نظر به اندازهٔ دلخواه کوچک خواهد شد. همانطور که این تفاضل به اندازهٔ دلخواه کوچک میشود، مقادیر احتمالی برای مساحت شکل مورد نظر توسط کران پایین دنبالهٔ مساحتها به نحوی سازمانیافته «اِفنا میشوند». این ایده از آنتیفون در قرن پنجم پیش از میلاد نشئت میگیرد اما کاملاً مشخص نیست که او به چه میزان درک درستی از این روش داشتهاست.
- ↑ عدد پی ()، یک ثابت ریاضیاتی است. این ثابت به صورت نسبت محیط دایره به قطرش تعریف شده و تعاریف معادل مختلفی نیز دارد. این عدد در بسیاری از فرمولهای ریاضیاتی، در تمام زمینههای ریاضیات و فیزیک ظاهر میشود. قدیمیترین استفاده از حرف یونانی جهت نمایش نسبت محیط دایره به قطرش، توسط ریاضیدان ویلزی به نام ویلیام جونز در ۱۷۰۶ میلادی بر میگردد. این ثابت تقریباً برابر با ۳٫۱۴۱۵۹ بوده و برخی مواقع به آن ثابت ارشمیدس هم گفته میشود.
- ↑ قضیهٔ فیثاغورس در هندسه اقلیدسی است که بر اساس آن، در یک مثلث راستگوشه (قائمالزاویه)، همواره مجموع مربعهای دو ضلع برابر با مربع وتر است. این قضیه به نام ریاضیدان یونانی فیثاغورس نامگذاری شدهاست. وارون این قضیه نیز درست است، به عبارت دیگر، اگر باشد، مثلث قائمالزاویه است. اثبات عکس قضیه فیثاغورس را به اقلیدس نسبت دادهاند. این قضیه بارها به روشهای مختلف هندسی و جبری اثبات شدهاست که برخی از این اثباتها به هزاران سال گذشته برمیگردند.
- ↑ حساب مقدماتی همان عملیات های جمع،تفریق،ضرب و تقسیم است.
- ↑ دستگاه اعداد پایه ۶۰ (بر مبنای ۶۰) نوعی سامانه شمارش است که در آن عدد شصت به عنوان مبنا و پایه شمارش محسوب میشود. سومریان باستان این روش شمارش را سه هزار سال پیش از میلاد ابداع کردند و سپس آن را به بابلیان منتقل کردند. این شیوه شمارش به شکل اصلاح شده هنوز هم در اندازهگیری زمان، زاویه و مختصات جغرافیایی کاربرد دارد. عدد شصت، عددی است که بخش پذیری بالایی دارد، و به دوازده فاکتور یا مقسوم علیه، یعنی {۱، ۲، ۳، ۴، ۵، ۶، ۱۰، ۱۲، ۱۵، ۲۰، ۳۰، ۶۰} بخش پذیر است که از بین آنها ۲، ۳ و ۵ عدد اول هستند. با این بخش پذیری بالا، اعداد بدست آمده از تقسیم کردن آن بدون کسری بوده و بیان کردن آن سادهتر میشود. به عنوان مثال، یک ساعت را میتواند بهطور مساوی و بدون کسر، را به بخشهای از ۳۰ دقیقه، ۲۰ دقیقه، ۱۵ دقیقه، ۱۲ دقیقه، ۱۰ دقیقه، ۶ دقیقه، ۵ دقیقه، ۴ دقیقه، ۳ دقیقه، ۲ دقیقه و ۱ دقیقه تقسیم نمود، بدون اینکه نیازی به استفاده از ثانیه باشد. همچنین شصت کوچکترین عددی است که به اعداد ۱ تا ۶ بخش پذیر است و بنابراین کوچکترین مضرب مشترک اعداد ۱ تا ۶ میباشد.
- ↑ زاویه (به انگلیسی: Angle) یا گوشه یا کُنجه یکی از مفاهیم هندسه است و از برخورد دو خط مستقیم ساخته میشود؛ یکای اندازهگیری زاویه درجه است که میان دو نیمخط که سری مشترک دارند محصور شدهاست. به سر مشترک این دو نیمخط رأسِ زاویه میگویند. بزرگی یک زاویه «مقدار چرخشی» (دورانی) است که دو نیمخط از گوشهٔ زاویه نسبت به یکدیگر دارند، با بدست آوردن طول کمانی پدید آمده در اثر چرخش میتوان اندازهٔ زاویه را بدست آورد. زاویه عبارت است از شکلی که از دوران دو قطعه خط پیرامون یک نقطه پدید آید.
- ↑ در ریاضیات، مقطع مخروطی (یا به سادگی مخروطی، گاهی اوقات منحنی درجه دوم نامیده می شود) منحنی است که به عنوان تقاطع سطح یک مخروط با یک صفحه به دست می آید. سه نوع مقطع مخروطی عبارتند از: هذلولی، سهمی و بیضی. دایره یک مورد خاص از بیضی است، اگرچه از نظر تاریخی گاهی اوقات آن را نوع چهارم می نامند. ریاضیدانان یونان باستان برش های مخروطی را مطالعه کردند که در حدود 200 سال قبل از میلاد با کار سیستماتیک آپولونیوس پرگا بر روی خواص آنها به اوج خود رسید.
- ↑ مثلثات شاخه ای از ریاضیات است که روابط میان طول اضلاع و زاویههای مثلث را مطالعه میکند. نخستین کاربرد مثلثات در مطالعات اخترشناسی بودهاست. اکنون مثلثات کاربردهای زیادی در زمينههاي ریاضیات محض و کاربردی، فيزيك و... دارد. بعضی از روشهای بنیادی تحلیل، مانند تبدیل فوریه و معادلات موج، از توابع مثلثاتی برای توصیف رفتار تناوبی موجود در بسیاری از فرآیندهای فیزیکی استفاده میکنند. همچنین مثلثات، پایهی علم نقشهبرداری است. سادهترین کاربرد مثلثات در مثلث قائمالزاویه است. هر شکل هندسی دیگری را نیز میتوان به مجموعهای از مثلثهای قائمالزاویه تبدیل کرد. شکل خاصی از مثلثات، مثلثات کروی است که برای مطالعهی مثلثات روی سطوح کروی و منحنی به کار میرود.
- ↑ سینوس نوعی تابع مثلثاتی برای یک زاویه است.
- ↑ کسینوس یکی از نسبتهای مثلثاتی است. اصطلاح قدیمی این نسبت در ریاضیات و اخترشناسی قدیم جَیب تمام بودهاست
- ↑ مثلثات کروی علمی است که به بررسی روابط بین زاویهها و اضلاع یک مثلث کروی (در هندسه نااقلیدسی) میپردازد. مثلثات کروی شاخهای از هندسه کروی است که با توجه به روابط بین توابع مثلثاتی دو طرف و زوایای چند ضلعی کروی (به ویژه مثلث کروی)؛ محدود شده توسط تعدادی از دایرههای بزرگ، در کره را بررسی میکند. کاربرد عملی مثلثات کروی در محاسبهها و براوردها در نجوم رصدی، زمینشناسی و ناوبری، و نیز قبله یابی، بسیار مهم است.
- ↑ اعشار یا سیستم ده دهی،یک سیستم بر اساس اعداد 10 است و دقیق تر از سیستم اعداد60 است
- ↑ نظریهٔ ماتریس یکی از نظریاتیاست که در حالتهای خاص میتواند توصیف دقیق از نظریه-م ارائه دهد. عملاً به همهٔ مدلهای مکانیک کوانتومی که آن درجههای آزادی به صورت ماتریس نشان دادهشدهاند نظریهٔ ماتریس میگویند. در واقع برای توصیف نظریهٔ در زمینههای مختلف نظریههای ماتریس مختلفی وجود دارد.این نظریه توهمی و انتزاعی است
- ↑ نظریه اعداد (در گذشته به آن حساب یا حساب پیشرفته میگفتند) شاخهای از ریاضیات محض است که خود را عمدتاً وقف مطالعهٔ اعداد صحیح نمودهاست. کارل گاوس گفت: «ریاضیات ملکهٔ علوم است، و نظریهٔ اعداد ملکه ریاضیات.» نظریه اعداد دانان به مطالعه اعداد اول و همچنین خواص اشیائی که از اعداد ساخته میشوند میپردازند، (به عنوان مثال اعداد گویا) یا تعمیمهایی از اعداد تعریف میکنند (مثل اعداد صحیح جبری).
- ↑ آمار را باید علم استخراج و توسعهٔ دانشهای تجربی و انسانی با استفاده از روشهای گردآوری و تحلیل دادههای تجربی (حاصل از اندازهگیری و آزمایش) دانست. روشهای محاسباتی جدیدتر توسط رایانه همچون یادگیری ماشینی، و کاوشهای ماشینی در دادهها، در واقع، امتداد و گسترش دانش آمار به عهد محاسبات نو و دوران اعمال شیوههای ماشینی بوده و امروزه علم آمار را به علم بیان علوم دیگر مبدل ساختهاست.
- ↑ ریاضیات کاربردی شاخهای از ریاضیات است که از یک سو به کاربرد ریاضیات در رشتههای دیگر (مدل) میپردازد، و از سوی دیگر سعی دارد مبانی نظری ریاضیات محض را به مبانی عملی نزدیکتر کند و به عنوان پلی بین ریاضیات محض و علوم کاربردی عمل کند. از زمینههای مختلف آن، میتوان به آنالیز عددی، نظریهٔ معادلات دیفرانسیل، بهینهسازی، نظریه اطلاعات، نظریه بازیها و فیزیک ریاضی اشاره کرد.
- ↑ ریاضیات محض (به انگلیسی: Pure Mathematics) به مطالعه مفاهیم ریاضیاتی مستقل از هر نوع کاربرد خارج از دایره ریاضیات می پردازد. این مفاهیم ممکن است از دغدغه های جهان واقعی نشأت گرفته باشند، و نتایج آن بعدها برای کاربرد های عملی مفید واقع شوند، اما ریاضیات محض ابتداءً از چنان کاربردهای عملی انگیزه نمی گیرد. در مقابل، جذابیت رهیافت محض در ریاضی مربوط به چالشها و جنبههای زیباشناختی مفاهیم منطقیست. مفاهیمی که خود پیامدهایی از اصول پایه ای تری می باشند.
- ↑ علوم ریاضی (به انگلیسی: Mathematical sciences) یک اصطلاح گسترده است که به رشتههای دانشگاهيی اشاره دارد که زمینهٔ اصلی آنها ریاضی است، اما بهطورکلی ممکن است تنها به مسائل ریاضی نپردازند. بهطور مثال، آمار، رشتهای است که از روشهای ریاضی استفاده میکند، ولی اهداف خاصی را در سایر علوم غیر از ریاضی دنبال میکند. علم کامپیوتر، علم محاسبات، تحقیق در عملیات، رمزشناسی، فیزیک نظری و علم آمار شاخههای دیگری هستند که میتوان آنها را بهعنوان علوم ریاضی در نظر گرفت.
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
فلسفه ریاضیات
فلسفهٔ ریاضیات (به انگلیسی: Philosophy of mathematics)، شاخهای از فلسفه است که به بنیادهای وجودیِ ریاضیات و مباحث مربوط به معرفتشناسی ریاضیات میپردازد. از مکتبهای فلسفهٔ ریاضی میتوان به منطقگرایی، شهودگرایی، صورتگرایی و افلاطونگرایی اشاره کرد.
مکاتب فلسفه ریاضی
[ویرایش]منطقگرایی
[ویرایش]آموزه منطقگرایی عبارت از این است که مفاهیم و قضایای ریاضی به مفاهیم و قضایای منطقی فروکاهیده شود. نظریه کانت دربارهٔ ریاضیات دچار انتقاداتی بود که به ظهور منطقگرایی نزد برنارد بولتسانو انجامید.
شهودگرایی
[ویرایش]لویتزن اگبرتوس ژان براوئر که مختصراً براوئر نیز نامیده میشود ریاضیدان و فیلسوف هلندی است که نام شهودگرایی در ریاضیات را بر سر زبانها انداخت. بر اساس شهودگرایی، ریاضیات مخلوق ذهن است و صدقهای جملات گزارههای ریاضی صرفاً میتوانند از طریق ساختارهای ذهنی ای درک و فهمیده شوند که اثبات میکند آن گزاره صادق است و ارتباط بین ریاضی دانان صرفاً وسیله ای است که میتواند فرایندهای ذهنی یکسانی در اذهان گوناگون را به وجود آورد.
صورتگرایی
[ویرایش]در این دیدگاه ریاضیات علم نیست، زیرا موضوع مادی مورد مطالعه ندارد، مفروضاتی شهودی و بینشی ندارد تا بتواند به آنها تعبیری بدهد. ریاضیات یک زبان است. ریاضیات وسیله فرمولبندی کردن و توسعه نظریههای علمی است. فرمالیسم یا همان صورتگرایی ریاضی عنوانی است که به نظریه دیوید هیلبرت داده شده است، چرا که در صورتگرایی تکیه بر جنبهٔ صوری ریاضیات در مقابل معنی یا محتواست و کمابیش مبتنی بر انکار محتوا برای فرمولهای ریاضی است. هیلبرت اساساً سعی داشت تا ریاضیات را بر پایههای صرفاً صوری واصل موضوعی استوار سازد. در این دیدگاه، صدق یک نظریهٔ ریاضی بدین معنی است که آن نظریه تناقضی به بار نیاورد و منجر به تناقض نگردد. صورتگرایان برخلاف منطقگرایان بنیاد ریاضیات را نه در منطق، بلکه صرفاً در مجموعهای از نمادهای صوری میدانند، آنگاه ریاضیات را یک نظام صوری متشکل از احکام ریاضی که تنهادارای صورت هستند، میانگارند.
پرسشها
[ویرایش]از جمله پرسشهایی که فلسفهٔ ریاضی، کوشش در پاسخ به آن دارد، اینها است:
- منشأ موضوعات ریاضی چه هستند؟
- وضعیت وجودی مفاهیم ریاضی چیست؟
- اشاره به یک شیء ریاضی به چه معناست؟
- شخصیت یک گزارهٔ ریاضی چیست؟
- رابطهٔ بین منطق و ریاضیات چیست؟
- نقش هرمنوتیک در ریاضیات چیست؟
- تحقیق ریاضی به چه معناست و چگونه ممکن است؟
- چه چیزی باعث توانایی ریاضی در تبیین تجربیات میشود؟
- نقش ذهن انسان در تولید ریاضیات چیست؟
- زیبایی ریاضی به چه معناست؟
- منبع و ماهیت حقیقت ریاضی چیست؟
- چه رابطهای بین جهان انتزاعی ریاضیات و جهان مادی وجود دارد؟
در آغاز قرن بیستم، سه مکتب فلسفهٔ ریاضی برای پاسخگوئی به اینگونه پرسشها بهوجود آمد. این سه مکتب به نامهای شهودگرایی و منطقگرایی و صورتگرایی معروفاند.
منابع
[ویرایش]ویکی پدیای فارسی
جوایز ریاضیات
جوایز ریاضیات شامل مدال فیلدز (نوبل ریاضی)، جایزه وولف و ... است.
جایزه فیلدز
[ویرایش]مدال فیلدز جایزهای است که به دو، سه یا چهار ریاضیدان زیر ۴۰ سال در کنگره بینالمللی اتحادیه بینالمللی ریاضی (IMU) اهدا میشود، نشستی که هر چهار سال یکبار برگزار میشود. نام این جایزه به افتخار ریاضیدان کانادایی جان چارلز فیلدز است.
مدال فیلدز یکی از بالاترین افتخاراتی است که یک ریاضیدان میتواند دریافت کند، و به عنوان جایزه نوبل ریاضیات توصیف شده است، اگرچه چندین تفاوت عمده وجود دارد، از جمله فراوانی جایزه، تعداد جوایز، محدودیتهای سنی، ارزش پولی، و معیارهای جایزه. طبق نظرسنجی سالانه تعالی دانشگاهی توسط ARWU، مدال فیلدز به طور مداوم به عنوان بهترین جایزه در زمینه ریاضیات در سراسر جهان در نظر گرفته میشود، و در نظرسنجی دیگری که توسط IREG در سال ۲۰۱۳-۲۰۱۴ انجام شد، مدال فیلدز به دست آمد. بعد از جایزه هابیلبه عنوان دومین جایزه معتبر بینالمللی در ریاضیات.
این جایزه شامل یک جایزه پولی است که از سال ۲۰۰۶، ۱۵۰۰۰ دلار کانادا بوده است. فیلدز در ایجاد جایزه، طراحی مدال خود، و تأمین مالی بخش پولی نقش داشت، اگرچه او قبل از تأسیس آن مرد و برنامهاش توسط جان لایتون سینج نظارت شد.
این مدال برای اولین بار در سال ۱۹۳۶ به ریاضیدان فنلاندی لارس آلفورس و ریاضیدان آمریکایی جسی داگلاس اعطا شد و از سال ۱۹۵۰ هر چهار سال یکبار اعطا میشود. هدف آن شناسایی و حمایت از محققان ریاضی جوانتر است که سهم عمدهای داشتهاند. در سال ۲۰۱۴، مریم میرزاخانی ریاضیدان ایرانی اولین زن مدال آور فیلدز شد. در مجموع، ۶۴ نفر مدال فیلدز را دریافت کردهاند.
جدیدترین گروه مدال آوران فیلدز جوایز خود را در ۵ ژوئیه ۲۰۲۲ در یک رویداد آنلاین دریافت کردند که از هلسینکی، فنلاند به صورت زنده پخش شد. در ابتدا قرار بود در سن پترزبورگ روسیه برگزار شود، اما پس از تهاجم روسیه به اوکراین در سال ۲۰۲۲ منتقل شد .
جایزه وولف
[ویرایش]جایزه ولف در ریاضی از ۱۹۷۸ تقریباً هرساله در اسرائیل اعطا میشود. وبسایت بنیاد ولف جایزه را سالانه میخواند ولی برخی جایزهها در بعضی سالها داده نشده و در بعضی سالها تقسیم شدهاست تا پیش از ایجاد جایزه آبل این جایزه نزدیکترین معادل جایزه نوبل در ریاضی بود زیرا جایزه پرافتخارتر مدال فیلدز تنها هر ۴ سال یک بار به ریاضیدانان زیر ۴۰ سال داده میشود.
جایزه آبل
[ویرایش]جایزهٔ آبل (به انگلیسی: Abel Prize) جایزهای است بینالمللی که هر ساله توسط شاه نروژ به یک یا چند ریاضیدان که کار ارزندهای در ریاضیات انجام داده باشد، داده میشود. این جایزه به افتخار ریاضیدان نروژی نیلس هنریک آبل (۱۸۲۹–۱۸۰۲) نامگذاری شده در سال ۲۰۰۱ توسط دولت نروژ بنیانگذاری شد.
منابع
[ویرایش]ویکی پدیای فارسی
شاخههای ریاضیات
شاخه های ریاضیات مربوط به علم هایی است که مربوط به ریاضیات نظری، پایه هستند، ریاضیات بیش از علوم طبیعی شاخه مختلف دارد مثل (حساب، حسابان، هندسه، آمار و احتمال، جبر و معادله، نظریه اعداد، آنالیز ریاضی و...) است.
حساب
[ویرایش]حِساب شاخه ای از ریاضیات است که شامل مطالعه اعداد، بهخصوص خواص عملیات سنتی روی آن ها یعنی جمع، تفاضل(تفریق)، ضرب و تقسیم می باشد. حساب قسمت مقدماتی نظریه اعداد می باشد و نظریه اعداد امروزه به عنوان یکی از اصلی ترین شاخه های ریاضیات (که جایگاه آن در بالاترین قسمت درخت تقسیم بندی گرایش های ریاضی قرار دارد) در نظر گرفته می شود. در کنار نظریه اعداد جبر، هندسه و آنالیز نیز جزو این شاخه های اصلی قرار دارند. عبارت حساب و حساب مرتبه بالاتر تا اوایل قرن بیستم به عنوان کلمه هم معنی نظریه اعداد به کار برده می شد و هنوز هم برای اشاره به قسمت اعظم نظریه اعداد به کار برده می شود.
ریاضیات کاربردی
[ویرایش]ریاضیات کاربردی شاخهای از ریاضیات است که از یک سو به کاربرد ریاضیات در رشتههای دیگر (مدل) میپردازد، و از سوی دیگر سعی دارد مبانی نظری ریاضیات محض را به مبانی عملی نزدیکتر کند و به عنوان پلی بین ریاضیات محض و علوم کاربردی عمل کند. از زمینههای مختلف آن، میتوان به آنالیز عددی، نظریهٔ معادلات دیفرانسیل، بهینهسازی، نظریه اطلاعات، نظریه بازیها و فیزیک ریاضی اشاره کرد.معمولاً به واسطهٔ مدلهای ریاضی ست که ریاضیّات را به زمینههای دیگر اعمال میکنند. به عنوان زیر شاخههای مهم ریاضیّات کاربردی، میشود از تحقیق در عملیات، دینامیک سیّالات، نسبیّت عددی (numerical relativity)، و معادلات ماکسول نام برد. همچنین بخشهای مهمی از مباحث مربوط به علوم کامپیوتر و آمار و احتمال نیز در این شاخه مورد بحث قرار میگیرند. بخش عظیمی از ریاضیات گسسته نیز در ارتباط تنگاتنگ با بخشهایی از ریاضیات کاربردی است.
ریاضیات محض
[ویرایش]ریاضیات محض یا ریاضیات نظری (به انگلیسی: Pure Mathematics) به مطالعه مفاهیم ریاضیاتی مستقل از هر نوع کاربرد خارج از دایره ریاضیات می پردازد. این مفاهیم ممکن است از دغدغه های جهان واقعی نشأت گرفته باشند، و نتایج آن بعدها برای کاربرد های عملی مفید واقع شوند، اما ریاضیات محض ابتداءً از چنان کاربردهای عملی انگیزه نمی گیرد. در مقابل، جذابیت رهیافت محض در ریاضی مربوط به چالشها و جنبههای زیباشناختی مفاهیم منطقیست. مفاهیمی که خود پیامدهایی از اصول پایه ای تری می باشند.
در حالی که ریاضیات محض به عنوان یک فعالیت از زمان یونان باستان وجود داشته است، اما تحول و جنبه های استادانه ی آن در حدود ۱۹۰۰ میلادی ظهور پیدا کرد، بعد از این که نظریه هایی با خواص ضد شهودی (مثل هندسه های غیر-اقلیدسی و نظریه کانتور مجموعه های نامتناهی)، و پارادوکس های ظاهری (چون توابع پیوسته ای که هیچ جا دیفرانسیل پذیر نیستند، و پارادوکس راسل) کشف شدند. این پدیده ها نیاز به تجدید مفهوم ریاضیات استوار (یا ریاضیات دقیق و سفت و سخت) و بازنویسی تمام ریاضیات بر اساس آن شد، به گونه ای که استفاده سیستماتیک از روش های اصول موضوعه ای ترویج پیدا کرد. این مسئله منجر به این شد که بسیاری از ریاضی دانان بر روی ریاضیات به خودی خود، یعنی ریاضیات محض متمرکز شوند.
اکنون ایجاد مرز مشخصی بین ریاضیات محض و کاربردی بیشتر جنبه فلسفی داشته یا مربوط به ترجیحات یک ریاضیدان خاص می شود و نمی توان به طور استوار و دقیق مرزشان را در ریاضیات تعیین کرد. به طور خاص، اتفاق عجیبی نخواهد بود اگر یک عضو دانشکده ریاضیات کاربردی خود را به عنوان ریاضیدان محض معرفی کند.
حسابان
[ویرایش]حسابان (یا حساب دیفرانسیل و انتگرال)، که در گذشته به آن حساب بینهایتکوچکها می گفتند شاخهای از ریاضی است. همانگونه که هندسه مطالعهی اشکال و جبر تعمیم عملیات حساب (چهار عمل اصلی) است، حسابان به مطالعهی ریاضیاتی تغییرات پیوسته می پردازد.
حسابان دارای دو شاخه: حساب دیفرانسیل و حساب انتگرالی است. حساب دیفرانسیل به مطالعه نرخ تغییرات و شیب منحنیها پرداخته در حالی که حساب انتگرالی به تجمع مقادیر و نواحی تحت منحنیها میپردازد. این دو شاخه توسط قضیهی اساسی حسابان، به یک دیگر مرتبط شده و از مفاهیم بنیادی همگرایی دنباله ها و سریهای نامتناهی به یک حد خوش تعریف استفاده میکنند.
حساب بینهایت کوچکها به طور مستقل در اواخر قرن هفدهم میلادی توسط ایزاک نیوتون و گوتفرید ویلهلم لایبنیز توسعه یافت. امروزه حسابان در علوم، مهندسی و اقتصاد کاربردهای گستردهای پیدا کرده است.
در آموزش ریاضی، حسابان نشانگر درسی مقدماتی از آنالیز ریاضی است که به طور عمده به مطالعه توابع و حدود میپردازد. کلمه حسابان (جمع آن calculi است) یک کلمه لاتین است که معنای اصلی آن سنگ کوچک است. به دلیل این که از تکه های سنگ برای محاسبات استفاده می کردند، معنای این کلمه تکامل یافته و این کاربرد را پیدا کرد. این موضوع شامل موارد دیگری از جمله حساب گزارهای، حساب ریچی، حساب تغییرات، حساب لامبدا و حساب فرآیندی نیز می شود.
هندسه
[ویرایش]هِندِسه (به یونانی: γεωμετρία، تلفظ: geometria، معنی: زمینسنجی)؛ ژِئو «زمین»، مِتریا «سنجش، اندازهگیری») شاخهای از ریاضیات است که با شکل، اندازه، موقعیت نسبی شکلها و ویژگیهای فضا سروکار دارد. ریاضیدانی که در شاخهٔ هندسه کار میکند هندسهدان نامیده میشود. هندسه بهطور مستقل در پارهای از تمدنهای اولیه به شکل بدنهای از دانش عملی در مورد طول، مساحت و حجم ظهور کرد و پایهریزی آن به عنوان یک دانش رسمی ریاضی در زمان تالس (قرن ششم پیش از میلاد) در غرب آغاز شد. در قرن سوم پیش از میلاد، هندسه توسط اقلیدس به شکل اصل موضوعی درآمده بود و کار اقلیدس (هندسه اقلیدسی) استانداردی را پایهریزی نمود که قرنها دنبال شد. ارشمیدس روشهای هوشمندانهای برای محاسبهٔ مساحت و حجم ارائه داد که در بسیاری موارد پیشرو حساب انتگرال جدید محسوب میشوند. دانش اخترشناسی و به ویژه نگاشتن مکان ستارهها و سیارهها روی کره آسمان و توصیف رابطهٔ بین حرکت اجسام آسمانی تا هزار و پانصد سال بعد منشا بسیاری از پرسشهای هندسی بود. هر دوی هندسه و اخترشناسی در دنیای کلاسیک بخشی از کوادریویم بودند که خود زیرمجموعهای از علوم مقدماتی هفتگانه بود که یادگیری آنها برای هر شهروند آزادی ضروری مینمود.
آمارواحتمال
[ویرایش]آمار
[ویرایش]آمار شاخهای از ریاضیات است که به گردآوری، تحلیل، و ارائه دادهها میپردازد. آمار را باید علم استخراج و توسعهٔ دانشهای تجربی انسانی با استفاده از روشهای گردآوری و تحلیل دادههای تجربی (حاصل از اندازهگیری و آزمایش) دانست. روشهای محاسباتی جدیدتر توسط رایانه همچون یادگیری ماشینی، و کاوشهای ماشینی در دادهها، در واقع، امتداد و گسترش دانش آمار به عهد محاسبات نو و دوران اعمال شیوههای ماشینی بوده و امروزه علم آمار را به علم بیان علوم دیگر مبدل ساختهاست.
احتمال
[ویرایش]بهطور ساده، احتمالات به شانس وقوع یک حادثه گفته میشود.احتمال معمولاً مورد استفاده برای توصیف نگرش ذهن نسبت به گزارههایی است که ما از حقیقت آنها مطمئن نیستیم. گزارههای مورد نظر معمولاً از فرم "آیا یک رویداد خاص رخ میدهد؟" و نگرش ذهن ما از فرم "چقدر اطمینان داریم که این رویداد رخ خواهد داد؟" است. میزان اطمینان ما، قابل توصیف به صورت عددی میباشد که این عدد مقداری بین ۰ و ۱ را گرفته و آن را احتمال می نامیم. هر چه احتمال یک رویداد بیشتر باشد، ما مطمئن تر خواهیم بود که آن رویداد رخ خواهد داد. در واقع میزان اطمینان ما از اینکه یک واقعه (تصادفی) اتفاق خواهد افتاد.
جبر و معادله
[ویرایش]جبر
[ویرایش]جَبر (وام واژه عربی الجبر بهمعنای «یکیسازی تکههای شکستهشده» و «شکستهبندی») به همراه نظریه اعداد، هندسه و آنالیز، یکی از وسیعترین شاخههای ریاضیات است. جبر در عمومیترین حالت خود به مطالعه این نمادهای ریاضیاتی می پردازد؛ و ریسمانیست که تقریباً تمام ریاضیات را با هم یکپارچه می کند. این شاخه شامل مباحث زیادی مثل حل معادلات مقدماتی تا مطالعه تجریدهایی چون گروهها، حلقهها و میدانها است. بخش های مقدماتی تر جبر را جبر مقدماتی می نامند؛ و بخش های مدرن آن را جبر مجرد یا جبر مدرن می خوانند. جبر مقدماتی اغلب بخش مهم مطالعه ریاضیات، علوم یا مهندسی به علاوه علوم کاربردی دیگری چون پزشکی و اقتصاد می باشد. جبر مجرد یکی از شاخه های اصلی ریاضیات پیشرفته است که عمدتاً توسط ریاضیدانان حرفه ای مطالعه می شود.
معادله
[ویرایش]معادله در ریاضیات بیان برابری دو چیز با استفاده از نمادهاست. در تمام معادلهها علامت تساوی (=) دیده میشود. هر معادله دو طرف دارد که در دو طرف علامت تساوی ظاهر میشوند. در حقیقت معادله نوعی ترازو است که تساوی هر دو وزن ۵۰-۵۰ یا برابر است.
واژه شناسی جبر و معادله
[ویرایش]جبر:به معنای جبران کردن.
معادله:به معنای عدالت و موجب تعادل.
منابع
[ویرایش]ویکی پدیای فارسی
ریاضیات گسسته
ریاضیات گسسته شاخهای از علم ریاضیات است که با عناصر گسسته ریاضیات(مثل کاربرد ریاضی در سیستم ها) سروکار دارد و نه عناصر پیوسته(مثل حساب،هندسه و...) و از جبر و حساب استفاده میکند. ریاضیات گسسته بهدلیل کاربردهای زیاد در علوم رایانه در دهههای گذشته کاربرد زیاد یافتهاست. مفاهیم و نشانههای ریاضیات گسسته برای مطالعه «الگوریتمهای رایانه» و «زبانهای برنامهنویسی» مورد استفاده قرار گرفتهاست. در بعضی دانشگاهها ریاضیات محدود به مفاهیمی از ریاضیات گسسته اطلاق میشود که در تجارت کاربرد داشتهاند؛ ولی ریاضیات گسسته به مباحث تخصصی علوم رایانه میپردازد.ریاضیات مفهومی جبری،حسابی،احتمالی و آماری دارد.در ریاضیات گسسته مفاهیم هندسی به روش گراف به صورت جبری و احتمالی صورت می گیرد

مجموعه اشیاء مورد مطالعه در ریاضیات گسسته می تواند متناهی یا نامتناهی باشد. اصطلاح ریاضیات محدود گاهی اوقات به بخش هایی از رشته ریاضیات گسسته که با مجموعه های محدود سر و کار دارد، به ویژه آن دسته از حوزه های مرتبط با تجارت به کار می رود.
تحقیقات در ریاضیات گسسته در نیمه دوم قرن بیستم تا حدودی به دلیل توسعه رایانه های دیجیتال افزایش یافت. که در مراحل "گسسته" کار می کنند و داده ها را در بیت های "گسسته" ذخیره می کنند. مفاهیم و نمادهای ریاضیات گسسته در مطالعه و توصیف اشیاء و مسائل در شاخههای علوم کامپیوتر مانند الگوریتمهای کامپیوتر ، زبانهای برنامهنویسی ، رمزنگاری ، اثبات قضایای خودکار و توسعه نرمافزار مفید هستند . برعکس، پیادهسازیهای کامپیوتری در کاربرد ایدهها از ریاضیات گسسته تا مسائل دنیای واقعی مهم هستند.
اگرچه موضوعات اصلی مطالعه در ریاضیات گسسته اشیاء گسسته هستند، روش های تحلیلی از ریاضیات "پیوسته" نیز اغلب به کار گرفته می شود.
در برنامه های درسی دانشگاه، "ریاضیات گسسته" در دهه 1980 ظاهر شد، در ابتدا به عنوان یک دوره آموزشی پشتیبانی از علوم کامپیوتر. محتوای آن در آن زمان تا حدودی تصادفی بود. برنامه درسی پس از آن در ارتباط با تلاش های ACM و MAA به دوره ای تبدیل شد که اساساً در نظر گرفته شده است تا بلوغ ریاضی را در دانش آموزان سال اول توسعه دهد. بنابراین امروزه پیش نیاز رشته ریاضی در برخی از دانشگاه ها نیز می باشد. برخی از کتاب های درسی ریاضیات گسسته در سطح دبیرستان نیز ظاهر شده اند. در این سطح، ریاضیات گسسته گاهی اوقات به عنوان یک دوره مقدماتی در نظر گرفته می شود، که از این نظر بی شباهت به پیش حساب نیست .
تاریخچه ریاضیات گسسته
[ویرایش]عمدهٔ پیشرفتی که از اواسط قرن ۱۷ میلادی در ریاضیات صورت گرفت، در حساب دیفرانسیل و انتگرال بود که به خواص عدد حقیقی و تابعهای از این مجموعه بود. مطالعهٔ این مجموعههای ناشمارا منجر به به وجود آمدن مفاهیم پیوستگی و مشتق گردید و به این دلیل این ریاضیات را ریاضیات پیوسته میخوانند. اما در مقابل این گونه ریاضیات مفاهیم دیگری در ریاضیات وجود دارند که روی مجموعههای متناهی و شمارا قابل تعریفاند. به مجموعهٔ این مفاهیم ریاضی، ریاضیات گسسته گویند. ریاضیات گسسته در سالهای اخیر و به دلیل پیشرفت دانش کامپیوتر بیشترین رشد خود را در تاریخ ریاضیات داشتهاست.ریاضیات گسسته بعد از چندین سال به صورت یک مفهوم علمی ظاهر شد و یکی از علم های مهم در ریاضی است.امروزه ریاضیات گسسته علاوه بر کاربرد های کامپیوتر در کاربردی های رمز نگاری،داده های رابطه،تدارکات کامپیوتری،اعداد تصادفی و... می پردازد.
مباحث ریاضیات گسسته
[ویرایش]علوم کامپیتوری نظری
[ویرایش]علم کامپیوتر نظری شامل حوزه هایی از ریاضیات گسسته مرتبط با محاسبات است. این به شدت از نظریه گراف و منطق ریاضی استفاده می کند. در علم کامپیوتر نظری، مطالعه الگوریتم ها و ساختارهای داده گنجانده شده است. محاسبه پذیری آنچه را که اصولاً می توان محاسبه کرد، مطالعه می کند و پیوندهای نزدیکی با منطق دارد، در حالی که پیچیدگی زمان، مکان و سایر منابع گرفته شده توسط محاسبات را مطالعه می کند. تئوری خودکار و نظریه زبان رسمی ارتباط نزدیکی با قابلیت محاسبه دارند. شبکههای پتری و جبرهای فرآیندی برای مدلسازی سیستمهای کامپیوتری و روشهایی از ریاضیات گسسته در تجزیه و تحلیل VLSI استفاده میشوند.مدارهای الکترونیکی. هندسه محاسباتی الگوریتم ها را برای مسائل هندسی و نمایش اشیاء هندسی به کار می برد، در حالی که تجزیه و تحلیل تصویر کامپیوتری آنها را برای نمایش تصاویر به کار می برد. علم کامپیوتر نظری نیز شامل مطالعه موضوعات مختلف محاسباتی پیوسته است.
نظریه اطلاعات
[ویرایش]نظریه اطلاعات شامل کمی سازی اطلاعات است. نظریه کدگذاری که برای طراحی روشهای انتقال و ذخیرهسازی دادهها کارآمد و قابل اعتماد استفاده میشود، ارتباط نزدیک دارد . تئوری اطلاعات نیز شامل موضوعات پیوسته ای مانند: سیگنال های آنالوگ ، کدگذاری آنالوگ ، رمزگذاری آنالوگ است.
منطق ریاضیات
[ویرایش]منطق مطالعه اصول استدلال و استنباط معتبر و همچنین قوام ، درستی و کامل بودن است. به عنوان مثال، در بیشتر سیستم های منطق (اما نه در منطق شهودی ) قانون پیرس ((( P → Q ) → P ) → P ) یک قضیه است. برای منطق کلاسیک، می توان آن را به راحتی با یک جدول حقیقت تأیید کرد . مطالعه برهان ریاضی از اهمیت ویژه ای در منطق برخوردار است و برای اثبات قضیه خودکار و تأیید رسمی نرم افزار کاربرد دارد.
فرمول های منطقی ساختارهای گسسته ای هستند، همانطور که اثبات ها هستند، که درخت های محدود یا، به طور کلی، ساختارهای گراف غیر چرخه ای جهت دار تشکیل می دهند (با هر مرحله استنتاج ترکیب یک یا چند شاخه مقدماتی برای ارائه یک نتیجه واحد). مقادیر صدق فرمولهای منطقی معمولاً یک مجموعه محدود را تشکیل میدهند که عموماً به دو مقدار محدود میشود: درست و نادرست ، اما منطق نیز میتواند دارای ارزش پیوسته باشد، به عنوان مثال، منطق فازی . مفاهیمی مانند درختان اثبات نامحدود یا درختان مشتق نامتناهی نیز مورد مطالعه قرار گرفته اند، به عنوان مثالمنطق بی نهایت .
تئوری مجموعه ها
[ویرایش]نظریه مجموعهها شاخهای از ریاضیات است که مجموعهها را که مجموعهای از اشیاء هستند، مانند {آبی، سفید، قرمز} یا مجموعه (بی نهایت) همه اعداد اول را مطالعه میکند. مجموعه ها و مجموعه های جزئی مرتب شده با روابط دیگر در چندین زمینه کاربرد دارند.
در ریاضیات گسسته، مجموعه های قابل شمارش (از جمله مجموعه های محدود ) تمرکز اصلی هستند. شروع نظریه مجموعه ها به عنوان شاخه ای از ریاضیات معمولاً با کار جورج کانتور در تمایز بین انواع مختلف مجموعه های نامتناهی با انگیزه مطالعه سری های مثلثاتی مشخص می شود و توسعه بیشتر نظریه مجموعه های نامتناهی خارج از محدوده گسسته است. ریاضیات در واقع، کار معاصر در نظریه مجموعههای توصیفی از ریاضیات پیوسته سنتی استفاده گسترده میکند.
ترکیبات
[ویرایش]ترکیب شناسی روشی را مطالعه می کند که در آن ساختارهای گسسته می توانند ترکیب یا چیده شوند. ترکیبات شمارشی بر شمارش تعداد اشیاء ترکیبی خاص متمرکز است - به عنوان مثال روش دوازده گانه یک چارچوب یکپارچه برای شمارش جایگشت ها، ترکیب ها و پارتیشن ها فراهم می کند . ترکیبات تحلیلی به شمارش (یعنی تعیین تعداد) ساختارهای ترکیبی با استفاده از ابزارهای تحلیل پیچیده و نظریه احتمال مربوط می شود . در مقایسه با ترکیبات شمارشی که از فرمول های ترکیبی صریح و توابع تولیدی استفاده می کند .برای توصیف نتایج، هدف ترکیبات تحلیلی به دست آوردن فرمول های مجانبی است. ترکیبات توپولوژیکی به استفاده از تکنیک هایی از توپولوژی و توپولوژی جبری / توپولوژی ترکیبی در ترکیبات مربوط می شود. تئوری طراحی مطالعه طرحهای ترکیبی است که مجموعهای از زیر مجموعهها با ویژگیهای تقاطع مشخص هستند . نظریه پارتیشن مسائل مختلف شمارش و مجانبی مربوط به پارتیشن های عدد صحیح را مطالعه می کند و ارتباط نزدیکی با سری q ، توابع ویژه وچند جمله ای های متعامد . نظریه پارتیشن در ابتدا بخشی از نظریه و تحلیل اعداد بود، اکنون بخشی از ترکیبات یا یک زمینه مستقل در نظر گرفته می شود. تئوری نظم مطالعه مجموعه های جزئی منظم ، متناهی و نامتناهی است.
نظریه گراف
[ویرایش]نظریه گراف، مطالعه گراف ها و شبکه ها ، اغلب به عنوان بخشی از ترکیب شناسی در نظر گرفته می شود، اما به اندازه کافی بزرگ و متمایز شده است، با مشکلات خاص خود، که به عنوان یک موضوع در نظر گرفته می شود. نمودارها یکی از موضوعات اصلی مطالعه در ریاضیات گسسته هستند. آنها یکی از رایج ترین مدل های سازه های طبیعی و ساخت بشر هستند. آنها می توانند انواع زیادی از روابط و پویایی فرآیند را در سیستم های فیزیکی، بیولوژیکی و اجتماعی مدل کنند. در علوم کامپیوتر، آنها می توانند شبکه های ارتباطی، سازماندهی داده ها، دستگاه های محاسباتی، جریان محاسبات و غیره را نشان دهند .نظریه گراف جبری پیوند نزدیکی با نظریه گروه دارد و نظریه گراف توپولوژیکی پیوند نزدیکی با توپولوژی دارد. نمودارهای پیوسته نیز وجود دارد . با این حال، در بیشتر موارد، تحقیقات در نظریه گراف در حوزه ریاضیات گسسته قرار می گیرد.
نظریه اعداد
[ویرایش]نظریه اعداد به خصوصیات اعداد به طور کلی، به ویژه اعداد صحیح مربوط می شود. کاربردهایی در رمزنگاری و تحلیل رمزی دارد، به ویژه با توجه به محاسبات مدولار ، معادلات دیوفانتین ، همخوانی های خطی و درجه دوم، اعداد اول و آزمایش اولیه . دیگر جنبه های گسسته نظریه اعداد شامل هندسه اعداد است. در تئوری اعداد تحلیلی ، از تکنیکهای ریاضیات پیوسته نیز استفاده میشود. موضوعاتی که فراتر از اشیاء گسسته هستند شامل اعداد ماورایی ، تقریب دیوفانتین ، تجزیه و تحلیل p-adic و فیلدهای تابع است.
کاربرد ها
[ویرایش]ریاضیات گسسته مطالعه ریاضیاتی است که به مجموعهای از اعداد صحیح محدود شدهاست. اگرچه مطالعه کاربردهای ریاضیات پیوسته مانند حساب و جبر و مقابله به بسیاری از محققین آشکار است، کاربرد ریاضیات گسسته ممکن است نخست مبهم به نظر آید. با این وجود، ریاضی گسسته پایههای بسیاری از رشتههای علمی در دنیای واقعی به خصوص علوم کامپیوتر را تشکیل میدهد. تکنیکهای اولیه در ریاضیات گسسته را میتوان در بسیاری از زمینههای مختلف استفاده شود.
کاربرد ریاضیات گسسته در رمزنگاری
[ویرایش]رشته رمزنگاری که مطالعه روی چگونگی ایجاد ساختارهای امنیتی و کلمه عبور برای کامپیوتر و دیگر سیستمهای الکترونیکی است، بهطور کامل در ریاضیات گسسته بنا شدهاست. این امر تا حدی به این دلیل است که کامپیوترها اطلاعات را به صورت گسسته ارسال میکند. یک بخش مهم از ریاضیات گسسته این است که اجازه میدهد تا رمزنگاران به ایجاد و با شکستن کلمات عبور عددی نمایند. از آنجا که کمیت پول و مقدار اطلاعات محرمانه دخالت میکند، رمزنگار، اول باید یک پس زمینه محکم در نظریه اعداد داشته باشد تا اینکه بتوانند نشان دهند که آنها میتوانند کلمات عبور امن و روشهای رمزگذاری مطمئن ارائه دهند.
پایگاه دادههای رابطه
[ویرایش]پایگاههای داده رابطه تقریباً در تمام سازمانهایی که باید پیگیر کارمندان، مشتریان یا منابع هستند، نقش دارد. تقریباً در هر سازمان است که باید پیگیری کارکنان، مشتریان یا منابع است. یک پایگاه داده رابطه، صفات از یک قطعه خاصی از اطلاعات را متصل میکند. به عنوان مثال، در یک پایگاه شامل اطلاعات مشتری، رابطه جنبههای مختلف این پایگاه، نام، آدرس، شماره تلفن و سایر اطلاعات مریض را اجازه میدهد تا با هم در ارتباط باشند و مورد استفاده قرار گیرند. این کار همه از طریق مفهوم ریاضی گسسته انجام میشود. پایگاه داده اجازه میدهد تا اطلاعات گروهبندی شود و مورده استفاده قرار داده شود. از آنجا که هر قطعه از اطلاعات و هر صفت متعلق به آن قطعه از اطلاعات گسستهاست، سازماندهی این چنین اطلاعاتی در یک پایگاه داده نیاز به روشهای ریاضیات گسسته دارد.
استفاده به عنوان تدارکات
[ویرایش]لجستیک مطالعه سازماندهی جریان اطلاعات، کالاها و خدمات است. بدون ریاضیات گسسته، تدارکات وجود نخواهد داشت. دلیل این است که تدارکات بهطور سنگین از نمودارها و نظریه گراف، که یک زیر رشته ریاضی گسستهاست، استفاده میکند. نظریه گراف اجازه میدهد تا مشکلات پیچیده تدارکات بهطور ساده به نمودارهای متشکل از گرهها و خطوط نمایش داده شوند. یک ریاضیدان میتواند این نمودارها را با توجه به روش نظریه گراف به منظور تعیین بهترین راه برای حمل و نقل یا حل دیگر مشکلات لجستیکی تجزیه و تحلیل کند.
الگوریتمهای کامپیوتری
[ویرایش]الگوریتم قوانینی است که توسط آن یک کامپیوتر عمل میکند. این قوانین از طریق قوانین ریاضیات گسسته ایجاد شدهاست. یک برنامهنویس کامپیوتر با استفاده از ریاضیات گسسته به طراحی الگوریتمهای کارآمد میپردازد. این طراحی شامل استفاده از ریاضی گسسته برای تعیین تعداد مراحلی که یک الگوریتم نیاز دارد کامل شود، که حاکی از سرعت الگوریتم است. به دلیل پیشرفتهای حاصل در کاربردی ریاضیات گسسته در الگوریتم، کامپیوترهای امروزی بسیار سریع تر از قبل اجرا و راه اندازی میشوند.
کاربردهای همنهشتی
[ویرایش]همنهشتیها کاربردهای زیادی در ریاضیات گسسته ،علوم کامپیوتر، و بسیاری از رشتههای دیگر دارد. در این مقاله سه کاربرد آن را معرفی میکنیم.
استفاده در تخصیص مکانهای حافظه به فایلهای کامپیوتری
[ویرایش]فرض کنید یک شماره شناسایی مشتری به طول ده رقم است. برای بازیابی سریع فایلهای مشتری، نمیخواهیم با استفاده از رکورد مشتری، یک خانهٔ حافظه اختصاص دهیم. در عوض، میخواهیم از یک عدد صحیح کوچکتر مربوط به شماره شناسایی استفاده کنیم. اینکار را میتوان با تابع درهمساز (hashing function) معروف است انجام داد.
تولید اعداد تصادفی
[ویرایش]ساختن دنبالهای از اعداد تصادفی برای الگوریتمهای تصادفی، برای شبیهسازیها، و نیز برای بسیاری از اهداف دیگر مهم هستند. ساختن یک دنباله از اعداد تصادفی واقعی خیلی دشوار است یا احتمالاً غیرممکن.
با استفاده از همنهشتی میتوان دنبالهای از اعداد شبه تصادفی تولید کرد. این اعداد تصادفی دارای این مزیت هستند که خیلی سریع ساخته میشوند و عیب آن در این است که در استفاده از این دنبالهها در کارهای مختلف باید پیشگوییهای زیادی داشته باشیم.
رقمهای کنترلی
[ویرایش]از همنهشتیها میتوان در برای تولید رقمهای کنترلی (check digit) شمارههای شناسایی از انواع مختلف نظیر شمارههای کد ورد استفاده در محصولات خرده فروشی، شمارههای مورد استفاده در کتابها، شمارههای بلیط هواپیمایی، و… استفاده کرد.
تابع درهمساز
[ویرایش]در عمل، تابعها ی در هم ساز مختلفی وجود دارد اما یکی از متداولترین آنها به شکل h(k)=k mod m است که در آن m تعداد خانههای حافظه موجود است. تابعهای در هم ساز به راحتی ارزیابی میشوند طوریکه مکان فایلها را به سرعت میتوان مشخص کرد. تابع در هم ساز (h(k ای نیاز را برطرف میکند. برای یافتن (h(k لازم است باقیمانده تقسیم k بر m را بدست آوریم. همچینی این تابع پوشا نیز هست.
روش همنهشتی خطی
[ویرایش]معمولترین روش استفاده شده برای تولید اعداد شبه تصادفی این روش همنهشتی خطی است.
رقمهای کنترلی
[ویرایش]از همنهشتیها در رشتههای رقمی برای کنترل خطاها استفاده میشود. یک روش معمول برای کشف خطاها در چنین رشتهای، افزودن یک رقم اضافی در پایان رشتهاست. این رقم پایانی یا رقم کنترلی، با استفاده از یک تابع خاص محاسبه میشود. آنگاه برای تعیین اینکه این یک رشته رقمی درست است، یک کنترل انجام میشود تا معلوم شود این رقم پایانی دارای مقدار درست است.
منابع
[ویرایش]ویکی پدیای انگلیسی
ویکی پدیای فارسی
حسابان
حسابان (یا حساب دیفرانسیل و انتگرال)، که در گذشته به آن حساب بینهایتکوچکها می گفتند شاخهای از ریاضی است. همانگونه که هندسه مطالعهی اشکال و جبر تعمیم عملیات حساب (چهار عمل اصلی) است، حسابان به مطالعهی ریاضیاتی تغییرات پیوسته می پردازد.
حسابان دارای دو شاخه: حساب دیفرانسیل و حساب انتگرالی است. حساب دیفرانسیل به مطالعه نرخ تغییرات و شیب منحنیها پرداخته در حالی که حساب انتگرالی به تجمع مقادیر و نواحی تحت منحنیها میپردازد. این دو شاخه توسط قضیهی اساسی حسابان، به یک دیگر مرتبط شده و از مفاهیم بنیادی همگرایی دنباله ها و سریهای نامتناهی به یک حد خوش تعریف استفاده میکنند.
حساب بینهایت کوچکها به طور مستقل در اواخر قرن هفدهم میلادی توسط ایزاک نیوتون و گوتفرید ویلهلم لایبنیز توسعه یافت. امروزه حسابان در علوم، مهندسی و اقتصاد کاربردهای گستردهای پیدا کرده است. [۱]
دوران باستان
[ویرایش]در دوره باستانی برخی از ایده ها به حساب انتگرالی منجر شدند. اما به نظر نمی رسد که این ایده ها منجر به رهیافتی نظام مند و استوار شده باشد. محاسبات حجم و مساحت، یکی از اهداف حساب انتگرالی است که می توان رد آن را در پاپیروس مسکو پیدا کرد (دودمان سیزدهم مصر، حدود ۱۸۲۰ قبل از میلاد)؛ اما فرمول های آن دستور العمل های ساده بدون هیچ نشانی از روشی مشخص بودند، به گونه ای که برخی از این دستور العمل ها فاقد مؤلفه های اصلی بودند.
از عصر ریاضیات یونانی، اودوکسوس (حدود ۴۰۸-۳۵۵ قبل از میلاد) از روش افنا (که قبل از کشف مفهوم حد، کاری شبیه به آن را انجام می داد) برای محاسبه مساحت ها و حجم ها استفاده می کرد، در حالی که ارشمیدس (حدود ۲۸۷-۲۱۲ قبل از میلاد) این ایده را بیشتر تکوین داد تا روش اکتشافی را اختراع کرد که شباهت به روش های حساب انتگرالی دارد.
دوران قرون وسطی
[ویرایش]در خاورمیانه، ابن هیثم (به لاتین: Alhazen) (965-1040 میلادی) فرمولی برای جمع توانهای چهارم بدست آورد. او از نتایجی که اکنون به آن انتگرال گیری این تابع میگوییم استفاده کرد، که چنین فرمولهایی برای جمع مربع اعداد صحیح و توان چهارم برای او امکان محاسبه حجم سهمیگون را نیز فراهم نمود.
در قرن چهاردهم، ریاضیدانان هندی روشی نا-استوار ارائه نمودند که شبیه دیفرانسیل گیری بود به گونهای که بر روی برخی توابع مثلثاتی قابل اعمال بود.
در اروپا، کار بنیادینی در قالب رساله بوناونتورا کاوالیری صورت گرفت. او بود که مدعی شد حجمها و مساحتها را باید به صورت جمع حجمها و مساحتهایی با مقاطع بینهایت کوچک نوشت. این ایدهها مشابه کار ارشمیدس در رساله اش به نام روش بود، اما معتقدند که رساله مذکور ارشمیدس در قرن ۱۳م مفقود شده و در قرن ۲۰م میلادی دوباره کشف شده، بنابر این کاوالیری از وجود آن آگاهی نداشته است.

دوران مدرن
[ویرایش]مطالعه رسمی حسابان، روش بینهایتکوچکهای کاوالیری و حساب تفاضلات متناهی که در اروپا در همان زمان ها تکوین یافته بود را گرد هم آورد. پیر دو فرما، مدعی شد که مفهوم "تا حد ممکن برابر" (او برای این مفهوم، به کمک زبان لاتین، کلمه adequality را ابداع نمود) را از دیوفانتوس الهام گرفته است. این مفهوم نمایانگر برابری در حد یک جمله خطای بی نهایت کوچک بود. ترکیب این مفاهیم توسط جان ویلیس، ایساک بارو و جیمز گرگوری بدست آمد که دو نفر اخیر دومین قضیه اساسی حساب را در حدود ۱۶۷۰ اثبات کردند.
قاعده ضرب و قاعده زنجیره ای، مفاهیم مشتقات مراتب بالاتر و سری تیلور، و توابع تحلیلی توسط ایزاک نیوتون و با استفاده از نمادگذاری عجیبی به کار گرفته شد تا توسط آن ها مسائلی را در ریاضی-فیزیک حل نماید. نیوتون در کار های خویش، ایده هایش را به گونه ای بازگو نمود تا با روش زمانه مطابقت داشته باشد، اینگونه که محاسبات بینهایتکوچکها را با معادل هندسیشان جایگزین نمود. او برای حل مسائلی چون حرکت سیاره ها، شکل سطح یک سیال دورانی، پهن شدگی کره زمین در قطبین (پخ شدگی در قطبین)، حرکت وزنه با سر خوردن روی یک چرخزاد، و بسیاری دیگر از مسائلی که در اثر خود (کتاب Principia Mathematica نوشته شده در ۱۶۸۷ میلادی) مورد بحث قرار داد، از روش حسابان استفاده کرد. او در آثار دیگر خود، بسط سری هایی برای توابع، شامل توان های کسری و غیر گویا به کار برد، به گونه ای که واضح بود که اصل سری تیلور را فهمیده است. اما او تمام این اکتشافات را منتشر نکرد و در آن زمان هنوز استفاده از روش بینهایتکوچکها بد سابقه بود و جنبه مناسبی نداشت.
این ایده ها به حساب بینهایتکوچکهای واقعی منجر شد که توسط گوتفرید ویلهلم لایبنیز سامان یافت. نیوتون در ابتدا لایبنیز را به سرقت علمی متهم کرد. او اکنون به عنوان مخترع و کمک کننده مستقل به حسابان به حساب می آید. کمک های او جهت ارائه مجموعه قواعد واضحی برای کار با مقادیر بینهایتکوچکها بود که امکان محاسبه مشتقات مراتب دوم و بالاتر را فراهم می کرد و قاعده ضرب و قاعده زنجیره ای را به فرم دیفرانسیلی و انتگرالی ارائه نمود. لایبنیز برعکس نیوتون، توجه بسیاری به صوری سازی می نمود، به گونه ای که اغلب روز ها صرف تعیین نماد مناسبی برای مفاهیم می نمود.
امروزه به هردوی لایبنیز و نیوتون جهت اختراع و توسعه مستقل حسابان اعتبار میدهند. نیوتون اولین کسی بود که حسابان را در فیزیک عمومی به کار برد و لایبنیز هم بخش زیادی از نمادگذاری به کار رفته در حسابان کنونی را اولین بار مورد استفاده قرار داد. بینش های پایه ای که هردوی نیوتون و لایبنیز ارائه نمودند شامل: قوانین دیفرانسیل گیری و انتگرال گیری، مشتقات مرتبه دوم و بالاتر و مفهوم تقریب زدن به کمک سری های چند جمله ای می شود. در زمان نیوتون، قضیه اساسی حساب شناخته شده بود.
از زمان لایبنیز و نیوتون، بسیاری از ریاضیدانان به تکوین پیوسته حسابان کمک کردند. یکی از اولین و کامل ترین کار هایی که هم بر روی حساب بینهایتکوچکها و هم حساب انتگرالی انجام شد، در سال ۱۷۴۸ توسط ماریا گائتنا آگنسی نوشته شد.
کاربرد
[ویرایش]استفاده از حساب بی نهایت کوچک برای مسائل فیزیک و نجوم با پیدایش علم معاصر بود. در تمام قرن هجدهم، این کاربردها چند برابر شد، تا اینکه لاپلاس و لاگرانژ در نزدیکی آن، طیف وسیعی از مطالعه نیروها را وارد قلمرو تحلیل کردند. معرفی نظریه پتانسیل به دینامیک را مدیون لاگرانژ (1773) هستیم، اگرچه نام "تابع بالقوه" و خاطرات اساسی موضوع به دلیل گرین است (1827، چاپ شده در 1828). نام "پتانسیل" به دلیل گاوس (1840) و تمایز بین تابع پتانسیل و بالقوه به کلازیوس است. با توسعه آن، نام های لژون دیریکله، ریمان، فون نویمان، هاینه، کرونکر، لیپسشیتز، کریستوفل، کیرشهوف، بلترامی و بسیاری از فیزیکدانان برجسته قرن مرتبط است.
در این مقاله نمیتوان وارد انواع کاربردهای دیگر تحلیل برای مسائل فیزیکی شد. از جمله تحقیقات اویلر در مورد آکوردهای ارتعاشی. سوفی ژرمن روی غشاهای الاستیک؛ پواسون، لامه، سن ونانت و کلبش در مورد کشش اجسام سه بعدی. فوریه در انتشار گرما. فرنل در نور; ماکسول، هلمهولتز، و هرتز در مورد برق. هانسن، هیل و گیلدن در مورد نجوم. ماکسول در مورد هارمونیک های کروی. لرد ریلی در مورد آکوستیک. و کمک های لژون دیریکله، وبر، کیرشوف، اف. زحمات هلمهولتز را باید به ویژه ذکر کرد، زیرا او به نظریههای دینامیک، الکتریسیته و غیره کمک کرد و قدرت تحلیلی عظیم خود را بر اصول اساسی مکانیک و همچنین در مورد ریاضیات محض به کار برد.
علاوه بر این، حساب بی نهایت کوچک به علوم اجتماعی وارد شد که با اقتصاد نئوکلاسیک شروع شد. امروزه ابزاری ارزشمند در جریان اصلی اقتصاد است.
پایه
[ویرایش]در حساب دیفرانسیل و انتگرال، مبانی به توسعه دقیق موضوع از بدیهیات و تعاریف اشاره دارد. در محاسبات اولیه، استفاده از مقادیر بی نهایت کوچک غیر دقیق تصور می شد و توسط تعدادی از نویسندگان، به ویژه میشل رول و اسقف برکلی به شدت مورد انتقاد قرار گرفت . برکلی در سال 1734 در کتاب خود به نام «تحلیلگر »، بینهایتها را بهعنوان ارواح مقادیر ناپدید شده توصیف کرد. ایجاد پایهای دقیق برای حساب دیفرانسیل و انتگرال، ریاضیدانان را در طول قرن بعد از نیوتن و لایبنیتس به خود مشغول کرد، و امروزه نیز تا حدودی یک حوزه فعال تحقیقاتی است.
چندین ریاضیدان، از جمله مکلارین ، سعی کردند صحت استفاده از بی نهایت کوچک را ثابت کنند، اما تا 150 سال بعد، به دلیل کار کوشی و وایرشتراس ، سرانجام راهی برای اجتناب از "مفاهیم" صرف از مقادیر بی نهایت کوچک پیدا شد. . پایه های حساب دیفرانسیل و انتگرال گذاشته شده بود. در Cours d'Analyse کوشی ، طیف وسیعی از رویکردهای بنیادی را مییابیم، از جمله تعریف تداوم بر حسب بینهایتها، و نمونه اولیه (تا حدودی نادقیق) از (ε, δ) - تعریف محدودیت در تعریف تمایز. وایرشتراس در کار خود مفهوم حد را رسمیت داد و بینهایت کوچکها را حذف کرد (اگرچه تعریف او در واقع می تواند بینهایت کوچکهای صفر مربع را تأیید کند ). به دنبال کار وایرشتراس، نهایتاً پایهگذاری حساب بر روی محدودیتها به جای کمیتهای بینهایت رایج شد، اگرچه این موضوع هنوز هم گاهی اوقات «حساب بینهایت کوچک» نامیده میشود. برنهارد ریمان از این ایده ها برای ارائه تعریف دقیقی از انتگرال استفاده کرد. همچنین در این دوره بود که با توسعه تجزیه و تحلیل پیچیده ، ایدههای حساب دیفرانسیل و انتگرال به سطح مختلط تعمیم داده شد .
در ریاضیات مدرن، مبانی حساب دیفرانسیل و انتگرال در حوزه تحلیل واقعی گنجانده شده است که شامل تعاریف و اثبات کامل قضایای حساب دیفرانسیل و انتگرال است. دسترسی به حساب دیفرانسیل و انتگرال نیز تا حد زیادی گسترش یافته است. هانری لبگو نظریه اندازه گیری را بر اساس پیشرفت های قبلی امیل بورل ابداع کرد و از آن برای تعریف انتگرال های همه به جز آسیب شناختی ترین توابع استفاده کرد. لورن شوارتز توزیعهایی را معرفی کرد که میتوان از آنها برای گرفتن مشتق از هر تابعی استفاده کرد.
محدودیت ها تنها رویکرد دقیق برای پایه و اساس حساب دیفرانسیل و انتگرال نیستند. راه دیگر استفاده از تحلیل غیراستاندارد آبراهام رابینسون است . رویکرد رابینسون، که در دهه 1960 توسعه یافت، از ماشین آلات فنی از منطق ریاضی برای تقویت سیستم اعداد واقعی با اعداد بی نهایت کوچک و نامتناهی استفاده می کند، همانطور که در مفهوم اصلی نیوتن-لایبنیتس بود. اعداد به دست آمده را اعداد فراواقعی می نامند و می توان از آنها برای ارائه یک توسعه لایبنیتس مانند قوانین معمول حساب استفاده کرد. همچنین تحلیل بی نهایت کوچک صاف وجود دارد، که با تجزیه و تحلیل غیر استاندارد تفاوت دارد زیرا نادیده گرفتن بینهایتهای کوچک با توان بالاتر را در طول اشتقاق الزامی میکند.
اهمیت
[ویرایش]در حالی که بسیاری از ایدههای حساب دیفرانسیل و انتگرال قبلاً در یونان ، چین ، هند ، عراق، ایران و ژاپن توسعه یافته بودند ، استفاده از حساب دیفرانسیل و انتگرال در قرن هفدهم، زمانی که آیزاک نیوتن و گوتفرید ویلهلم لایبنیتس بر اساس کار خود ساخته بودند، در اروپا آغاز شد. ریاضیدانان قبلی اصول اولیه آن را معرفی کردند. توسعه حساب دیفرانسیل و انتگرال بر اساس مفاهیم اولیه حرکت آنی و مساحت زیر منحنی ها ساخته شده است.
کاربردهای حساب دیفرانسیل شامل محاسبات مربوط به سرعت و شتاب ، شیب منحنی و بهینه سازی است. کاربردهای حساب انتگرال شامل محاسبات مربوط به مساحت، حجم ، طول قوس ، مرکز جرم ، کار و فشار است. برنامه های پیشرفته تر شامل سری های قدرت و سری فوریه است .
حساب دیفرانسیل و انتگرال نیز برای به دست آوردن درک دقیق تری از ماهیت فضا، زمان و حرکت استفاده می شود. برای قرنها، ریاضیدانان و فیلسوفان با پارادوکسهایی دست و پنجه نرم میکردند که شامل تقسیم بر صفر یا مجموع بینهایت اعداد بود. این سوالات در مطالعه حرکت و مساحت مطرح می شود. فیلسوف یونان باستان Zeno of Elea چندین نمونه معروف از این پارادوکس ها را بیان کرد. حساب دیفرانسیل و انتگرال ابزارهایی را فراهم می کند، به خصوص حد و سری بی نهایت ، که پارادوکس ها را حل می کند.
حدود و بینهایتکوچکها
[ویرایش]حسابان اغلب با کار روی مقادیر بسیار کوچک توسعه یافته است. از نظر تاریخی، اولین روش آن با کمک بینهایتکوچکها صورت گرفت. این ها اشیائی هستند که می توان با آن ها همچون اعداد حقیقی رفتار کرد، اما از جنبه هایی "بی نهایت کوچک" اند. به عنوان مثال، یک عدد بینهایتکوچک ممکن است بزرگتر از صفر باشد، اما کوچتر از هر عدد در دنباله باشد و لذا از هر عدد حقیقی مثبتی کوچکتر است. از این دیدگاه، حسابان گردایه ای از فنون دستکاری بینهایتکوچک هاست. نمادهای و را نماینده بینهایتکوچک ها و مشتق، یعنی را صرفاً نسبت این دو در نظر می گرفتند.
رهیافت بینهایتکوچک ها در قرن ۱۹م از دور خارج شد چون دقیق کردن مفهوم بینهایتکوچک کار سختی بود. با این حال، این مفهوم در قرن بیستم دوباره با معرفی مفهوم آنالیز غیر-استاندارد و آنالیز بینهایتکوچک های هموار که بنیان محکمی برای دستکاری بینهایتکوچک ها ارائه می نمود، زنده گشت.
در اواخر قرن نوزدهم، بینهایتکوچک ها در مجامع علمی با رهیافت اپسیلون و دلتا جهت تعریف حد جایگزین گشت. حدود مقادیر یک تابع را در یک ورودی خاص بر حسب مقادیرش در ورودی های مجاور توصیف می کند. این ابزار، رفتار مقیاس کوچک را در بستر دستگاه اعداد حقیقی دریافت می کند. در این رهیافت، حسابان را می توان گردایه ای از فنون برای دستکاری حدود خاصی در نظر گرفت. بینهایتکوچک ها با اعداد بسیار کوچک جایگزین شدند و رفتار بی نهایت کوچک یک تابع با رفتار حدی آن برای مقادیر اعداد کوچک و کوچک تر بدست می آید. تصور این بود که حدود بنیان استواری برای حسابان ارائه کرده و به همین دلیل این رهیافت در قرن بیستم تبدیل به رهیافتی استاندارد شد.
حساب دیفرانسیل
[ویرایش]
حساب دیفرانسیل به مطالعه تعریف، خواص و کاربردهای مشتق یک تابع می پردازد. فرآیند یافتن مشتق را دیفرانسیلگیری می نامند. اگر یک تابع و نقطه ای در دامنه آن را در نظر بگیریم، مشتق آن نقطه روشی است که رفتار مقیاس کوچک یک تابع نزدیک آن نقطه را در خود می گنجاند. با یافتن مشتق یک تابع در هر نقطه از دامنه آن، امکان تولید تابعی جدید به نام تابع مشتق یا صرفا مشتق تابع اصلی وجود دارد. به زبان صوری، مشتق عملگری خطی است که یک تابع را به عنوان ورودی گرفته و تابع دیگری را به عنوان خروجی تولید می کند. توصیف اخیر از بسیاری فرآیند های مورد مطالعه در جبر مقدماتی مجرد تر است، که ورودی و خروجی تابع صرفاً اعداد بودند. به عنوان مثال، اگر تابع دوبرابر کننده در نظر گرفته می شد، با ورودی عدد سه، خروجی عدد شش تولید می شد، و اگر تابع مربع سازی در نظر گرفته می شد، با گرفتن ورودی سه خروجی عدد نه می شد. در حالی که مشتق گیری کل تابع مربع ساز را به عنوان ورودی می گیرد، یعنی تمام اطلاعات مربوط به این که هر ورودی عددی آن تابع به چه خروجی عددی می رود، و از روی آن اطلاعات تابع دیگری می سازد که همان تابع دو برابر کننده است.
به زبان صریح تر، "تابع دو برابر کننده" را می توان به صورت نمایش داد و "تابع مربع ساز" را به صورت . اکنون "مشتق" تابع را که با عبارت "" تعریف می شود را به عنوان ورودی می گیرد و از روی آن تابع را تولید می کند.
رایج ترین نماد برای مشتق، نشانی شبیه به آپاستروف است که به آن پرایم (یا در فارسی پریم) می گویند. لذا، مشتق یک تابع مثل به صورت نوشته شده و آن را "اف پرایم" می خوانند. به عنوان مثال، اگر تابع مربع ساز باشد، آنگاه مشتق آن است (همان تابع دوبرابر کننده که در بالا بحث شد). این نمادگذاری به نمادگذاری لاگرانژ معروف است.
حساب دیفرانسیل و انتگرال در هر شاخه ای از علوم فیزیکی استفاده می شود، علوم اکچوئری ، علوم کامپیوتر ، آمار ، مهندسی ، اقتصاد ، بازرگانی ، پزشکی ، جمعیت شناسی و در سایر زمینه ها هرجا که بتوان مسئله ای را به صورت ریاضی مدل کرد و راه حل بهینه آن یافت می شود. دلخواه. این به شخص اجازه می دهد تا از نرخ تغییر (غیرثابت) به تغییر کل یا برعکس برود، و بارها در مطالعه یک مسئله یکی را می شناسیم و سعی می کنیم دیگری را پیدا کنیم. حساب دیفرانسیل و انتگرال را می توان در ارتباط با سایر رشته های ریاضی استفاده کرد. به عنوان مثال، می توان آن را با جبر خطی برای یافتن تقریب خطی "بهترین مناسب" برای مجموعه ای از نقاط در یک دامنه استفاده کرد. یا می توان از آن در نظریه احتمال برای تعیین مقدار انتظاری یک متغیر تصادفی پیوسته با توجه به تابع چگالی احتمال استفاده کرد. در هندسه تحلیلی ، برای مطالعه نمودارهای توابع، حساب دیفرانسیل و انتگرال برای یافتن نقاط بالا و پایین (حداکثر و حداقل)، شیب، تقعر و نقاط عطف استفاده می شود.. حساب دیفرانسیل و انتگرال نیز برای یافتن راه حل های تقریبی معادلات استفاده می شود. در عمل این روش استاندارد برای حل معادلات دیفرانسیل و انجام ریشه یابی در اکثر کاربردها است. به عنوان مثال روش هایی مانند روش نیوتن ، تکرار نقطه ثابت و تقریب خطی هستند. به عنوان مثال، فضاپیماها از تغییر روش اویلر برای تقریب مسیرهای منحنی در محیط های گرانش صفر استفاده می کنند.
فیزیک از حساب دیفرانسیل و انتگرال استفاده خاصی می کند. همه مفاهیم در مکانیک کلاسیک و الکترومغناطیس از طریق حساب دیفرانسیل و انتگرال به هم مرتبط هستند. جرم یک جسم با چگالی شناخته شده ، ممان اینرسی اجسام ، و انرژی های بالقوه ناشی از نیروهای گرانشی و الکترومغناطیسی را می توان با استفاده از حساب دیفرانسیل و انتگرال پیدا کرد. مثالی از استفاده از حساب دیفرانسیل و انتگرال در مکانیک، قانون دوم حرکت نیوتن است که می گوید مشتق تکانه جسم نسبت به زمان برابر با نیروی خالص است.بر روی آن از طرف دیگر، قانون دوم نیوتن را می توان با گفتن اینکه نیروی خالص برابر با جرم جسم ضربدر شتاب آن است، که مشتق زمانی سرعت و در نتیجه دومین مشتق زمانی موقعیت مکانی است بیان کرد. با شروع از دانستن چگونگی شتاب یک جسم، از حساب دیفرانسیل و انتگرال برای استخراج مسیر آن استفاده می کنیم.
نظریه الکترومغناطیس ماکسول و نظریه نسبیت عام انیشتین نیز به زبان حساب دیفرانسیل بیان شده اند. شیمی همچنین از حساب دیفرانسیل و انتگرال در تعیین نرخ واکنش استفاده می کند و در مطالعه واپاشی رادیواکتیو. در زیست شناسی، پویایی جمعیت با تولید مثل و نرخ مرگ و میر شروع می شود تا تغییرات جمعیت را مدل سازی کند.
قضیه گرین ، که رابطه بین یک انتگرال خط حول یک منحنی بسته ساده C و یک انتگرال دوگانه را بر روی ناحیه صفحه D محدود شده با C نشان می دهد، در ابزاری به نام پلان متر که برای محاسبه مساحت یک تخت استفاده می شود، اعمال می شود . سطح روی یک نقاشی به عنوان مثال، می توان از آن برای محاسبه مقدار مساحت اشغال شده توسط یک تخت گل یا استخر شنا با شکل نامنظم هنگام طراحی چیدمان یک قطعه استفاده کرد.
در قلمرو پزشکی، حساب دیفرانسیل و انتگرال را می توان برای یافتن زاویه انشعاب بهینه رگ خونی به منظور به حداکثر رساندن جریان استفاده کرد. حساب دیفرانسیل و انتگرال را می توان برای فهمیدن اینکه یک دارو با چه سرعتی از بدن دفع می شود یا سرعت رشد یک تومور سرطانی را می توان به کار برد.
در علم اقتصاد، محاسبات امکان تعیین حداکثر سود را با ارائه راهی برای محاسبه آسان هزینه نهایی و درآمد نهایی فراهم می کند .
انواع
[ویرایش]در طول سالها، بسیاری از فرمولبندیهای مجدد حساب دیفرانسیل و انتگرال برای اهداف مختلف مورد بررسی قرار گرفتهاند.
حساب غیر استاندارد
[ویرایش]محاسبات نادقیق با بینهایت کوچک به طور گسترده با تعریف دقیق (ε, δ) حد که از دهه 1870 شروع شد جایگزین شد. در همین حال، محاسبات با بینهایت کوچک ادامه داشت و اغلب به نتایج صحیح منتهی می شد. این امر باعث شد که آبراهام رابینسون بررسی کند که آیا امکان ایجاد یک سیستم اعداد با کمیت های بی نهایت کوچک وجود دارد که قضایای حساب دیفرانسیل و انتگرال هنوز معتبر هستند یا خیر. در سال 1960، با تکیه بر آثار ادوین هویت و جرزی لوش ، او موفق به توسعه تجزیه و تحلیل غیر استاندارد شد. تئوری تجزیه و تحلیل غیر استاندارد به اندازه کافی غنی است که در بسیاری از شاخه های ریاضیات قابل استفاده است. به این ترتیب، کتابها و مقالاتی که صرفاً به قضایای سنتی حساب اختصاص داده شده است، اغلب با عنوانحساب غیر استاندارد
تحلیل بی نهایت کوچک صاف
[ویرایش]این یکی دیگر از فرمول بندی مجدد حساب بر حسب بی نهایت کوچک است. بر اساس ایدههای FW Lawvere و با استفاده از روشهای نظریه مقولهها ، تمام توابع را پیوسته و ناتوان از بیان موجودیتهای گسسته میداند. یکی از جنبه های این فرمول این است که قانون وسط حذف شده در این فرمول بندی وجود ندارد.
تحلیل سازنده
[ویرایش]ریاضیات سازنده شاخهای از ریاضیات است که اصرار دارد که اثبات وجود یک عدد، تابع یا دیگر شیء ریاضی باید ساختاری از شیء را ارائه دهد. به این ترتیب ریاضیات سازنده قانون وسط حذف شده را نیز رد می کند . فرمول بندی مجدد حساب دیفرانسیل و انتگرال در یک چارچوب سازنده عموماً بخشی از موضوع تحلیل سازنده است.
پانویس
[ویرایش]
هندسه
هِندِسه(یا ژِئو «زمین»، مِتریا «سنجش، اندازهگیری») شاخهای از ریاضیات است که با شکل، اندازه، موقعیت نسبی شکلها و ویژگیهای فضا سروکار دارد. ریاضیدانی که در شاخهٔ هندسه کار میکند هندسهدان نامیده میشود. هندسه بهطور مستقل در پارهای از تمدنهای اولیه به شکل بدنهای از دانش عملی در مورد طول، مساحت و حجم ظهور کرد و پایهریزی آن به عنوان یک دانش رسمی ریاضی در زمان تالس (قرن ششم پیش از میلاد) در غرب آغاز شد. در قرن سوم پیش از میلاد، هندسه توسط اقلیدس به شکل اصل موضوعی درآمده بود و کار اقلیدس (هندسه اقلیدسی) استانداردی را پایهریزی نمود که قرنها دنبال شد. ارشمیدس روشهای هوشمندانهای برای محاسبهٔ مساحت و حجم ارائه داد که در بسیاری موارد پیشرو حساب انتگرال جدید محسوب میشوند. دانش اخترشناسی و به ویژه نگاشتن مکان ستارهها و سیارهها روی کره آسمان و توصیف رابطهٔ بین حرکت اجسام آسمانی تا هزار و پانصد سال بعد منشا بسیاری از پرسشهای هندسی بود. هر دوی هندسه و اخترشناسی در دنیای کلاسیک بخشی از کوادریویم بودند که خود زیرمجموعهای از علوم مقدماتی هفتگانه بود که یادگیری آنها برای هر شهروند آزادی ضروری مینمود.
تاریخ
[ویرایش]اولین آغاز ثبت شده هندسه را می توان در بین النهرین باستان و مصر در هزاره دوم قبل از میلاد ردیابی کرد. هندسه اولیه مجموعه ای از اصول کشف شده تجربی در مورد طول ها، زوایا، مساحت ها و حجم ها بود که برای رفع برخی نیازهای عملی در نقشه برداری ، ساخت و ساز ، نجوم و صنایع دستی مختلف توسعه یافت. اولین متون شناخته شده در مورد هندسه عبارتند از پاپیروس رایند مصر (2000-1800 قبل از میلاد) و پاپیروس مسکو (حدود 1890 قبل از میلاد) و الواح گلی بابلی ، مانند Plimpton 322 .(1900 قبل از میلاد). به عنوان مثال، پاپیروس مسکو فرمولی برای محاسبه حجم یک هرم کوتاه شده یا فروستوم ارائه می دهد. لوحهای گلی بعدی (350–50 قبل از میلاد) نشان میدهد که اخترشناسان بابلی روشهای ذوزنقهای را برای محاسبه موقعیت و حرکت مشتری در فضای سرعت-زمان اجرا کردند. این رویههای هندسی ماشینحسابهای آکسفورد ، از جمله قضیه سرعت متوسط را تا 14 قرن پیشبینی کردند. در جنوب مصر، نوبیای باستان سیستمی از هندسه شامل نسخههای اولیه ساعتهای خورشیدی ایجاد کردند.

در قرن هفتم قبل از میلاد، ریاضیدان یونانی تالس اهل میلتوس از هندسه برای حل مسائلی مانند محاسبه ارتفاع اهرام و فاصله کشتی ها از ساحل استفاده کرد. او را با اولین استفاده از استدلال قیاسی به کار رفته در هندسه، با استخراج چهار نتیجه به قضیه تالس، نسبت می دهند. فیثاغورث مکتب فیثاغورث را تأسیس کرد ، که اولین اثبات قضیه فیثاغورث به آن نسبت داده می شود ، اگرچه بیان این قضیه سابقه طولانی دارد. Eudoxus (408-حدود 355 قبل از میلاد) روش فرسودگی را توسعه داد.که امکان محاسبه مساحت ها و حجم ارقام منحنی را فراهم می کند، و همچنین نظریه نسبت هایی که از مشکل قدرهای غیرقابل مقایسه جلوگیری می کند ، که هندسه های بعدی را قادر می سازد پیشرفت های قابل توجهی داشته باشند. در حدود 300 سال قبل از میلاد، هندسه توسط اقلیدس متحول شد، او که «عناصرش» که به طور گستردهای موفقترین و تأثیرگذارترین کتاب درسی در تمام دوران به شمار میرود، دقت ریاضی را از طریق روش بدیهی معرفی کرد و اولین نمونه از قالبی است که امروزه در ریاضیات استفاده میشود. تعریف، بدیهیات، قضیه و برهان. اگر چه بیشتر مطالب عناصرقبلاً شناخته شده بودند، اقلیدس آنها را در یک چارچوب منطقی واحد و منسجم مرتب کرد. عناصر تا اواسط قرن بیستم برای همه تحصیلکردههای غرب شناخته شده بود و امروزه نیز مطالب آن در کلاسهای هندسه تدریس میشود . ارشمیدس (حدود 287-212 قبل از میلاد) سیراکوزی از روش خستگی برای محاسبه مساحت زیر کمان سهمی با جمع یک سری نامتناهی استفاده کرد و تقریبهای دقیقی از پی ارائه کرد. او همچنین مارپیچ نام خود را مطالعه کرد و فرمول هایی برای آن به دست آوردحجم سطوح انقلاب ریاضیدانان هندی نیز سهم مهمی در هندسه داشتند. Satapatha Brahmana (قرن 3 قبل از میلاد) شامل قوانینی برای ساخت و سازهای هندسی آیینی است که شبیه به Sulba Sutras است. بر اساس ( هایاشی 2005 ، ص 363)، سوتراهای اولبا حاوی "قدیمی ترین بیان شفاهی موجود از قضیه فیثاغورث در جهان است، اگرچه قبلاً برای بابلیان قدیم شناخته شده بود. آنها حاوی فهرست هایی از سه گانه فیثاغورثی هستند. که موارد خاصی از معادلات دیوفانتین است [ در نسخه خطی بخشعلیتعداد انگشت شماری از مسائل هندسی (از جمله مسائل مربوط به حجم جامدات نامنظم) وجود دارد. نسخه خطی بخشعلی نیز «نظام ارزش اعشاری با نقطه صفر را به کار می گیرد». Aryabhatiya Aryabhata ( 499) شامل محاسبه مساحت و حجم است. براهماگوپتا اثر نجومی خود را براهما اسفوتا سیدانتا در سال 628 نوشت. فصل 12، شامل 66 آیه سانسکریت ، به دو بخش تقسیم شد: "عملیات اساسی" (شامل ریشه های مکعب، کسرها، نسبت و نسبت، و مبادله مبادله ای) و "عملیات مبادله ای". مخلوط، سری های ریاضی، ارقام هواپیما، روی هم چیدن آجرها، اره کردن الوار، و انباشته شدن دانه ها). در بخش دوم، او قضیه معروف خود را در مورد قطرهای یک چهارضلعی حلقوی بیان کرد. فصل 12 همچنین شامل فرمولی برای مساحت چهارضلعی حلقوی (تعمیم فرمول هرون )، و همچنین توضیح کاملی از مثلث های گویا ( یعنی مثلث هایی با اضلاع گویا و مساحت های گویا) بود.

در قرون وسطی ، ریاضیات در اسلام قرون وسطی به توسعه هندسه، به ویژه هندسه جبری کمک کرد. المهانی (متولد 853) ایده کاهش مسائل هندسی مانند تکرار مکعب به مسائل جبر را در ذهن داشت. ثابت بن قره (معروف به لاتین به عنوان Thebit ) (901-836) با عملیات حسابی که برای نسبتهای کمیتهای هندسی اعمال میشود، سروکار داشت و به توسعه هندسه تحلیلی کمک کرد. عمر خیام (1048-1131) راه حل های هندسی معادلات مکعبی را یافت.. قضایای ابن هیثم (الحازن)، عمر خیام و نصیرالدین طوسی در مورد چهارضلعی ها، از جمله چهارضلعی لامبرت و چهارضلعی ساکری ، نتایج اولیه در هندسه هذلولی بود و همراه با فرض های جایگزین آنها، مانند به عنوان بدیهیات Playfair ، این آثار تأثیر قابل توجهی بر توسعه هندسه غیر اقلیدسی در میان هندسهسنجهای بعدی اروپایی، از جمله Witelo (حدود 1230-حدود 1314)، جرسونیدس (1288-1344)، آلفونسو ، جان والیس ، و جیووانی گیرولامو داشتند. ساچری.
در اوایل قرن هفدهم، دو پیشرفت مهم در هندسه رخ داد. اولین مورد ایجاد هندسه تحلیلی، یا هندسه با مختصات و معادلات ، توسط رنه دکارت (1596-1650) و پیر دو فرما (1601-1665) بود. این یک پیش درآمد ضروری برای توسعه حساب دیفرانسیل و انتگرال و علم کمی دقیق فیزیک بود. دومین توسعه هندسی این دوره، مطالعه سیستماتیک هندسه تصویری توسط ژیرار دسارگ (1591-1661) بود. هندسه فرافکنی به بررسی خواص اشکالی میپردازد که در زیر بدون تغییر هستندطرحها و بخشها ، بهویژه که به دیدگاه هنری مربوط میشوند .
دو پیشرفت در هندسه در قرن نوزدهم روش مطالعه قبلی آن را تغییر داد. اینها کشف هندسه های غیراقلیدسی توسط نیکولای ایوانوویچ لوباچفسکی، یانوس بولیای و کارل فردریش گاوس و فرمول بندی تقارن به عنوان ملاحظات اصلی در برنامه ارلانگن فلیکس کلاین (که اقلیدسی و غیر اقلیدسی را تعمیم داد) بود. ). دو تن از هندسهدانان چیره دست آن زمان برنهارد ریمان (1826-1866) بودند که عمدتاً با ابزارهایی از آنالیز ریاضی کار میکردند و سطح ریمان را معرفی میکردند ، و هانری پوانکاره ، بنیانگذارتوپولوژی جبری و نظریه هندسی سیستم های دینامیکی . در نتیجه این تغییرات عمده در مفهوم هندسه، مفهوم "فضا" به چیزی غنی و متنوع تبدیل شد و زمینه طبیعی تئوری هایی مانند تحلیل پیچیده و مکانیک کلاسیک متفاوت شد.
مفاهیم مهم اصلی
[ویرایش]بدیهیات
[ویرایش]اقلیدس در کتاب عناصر خود که یکی از تأثیرگذارترین کتابهایی است که تا کنون نوشته شده است ، رویکردی انتزاعی به هندسه داشت . اقلیدس بدیهیات یا فرضیه های خاصی را معرفی کرد که ویژگی های اولیه یا بدیهی نقاط، خطوط و سطوح را بیان می کرد. او با استدلال ریاضی به استنباط دقیق سایر خصوصیات پرداخت. ویژگی بارز رویکرد اقلیدس به هندسه سختی آن بود و به هندسه بدیهی یا ترکیبی معروف شد . در آغاز قرن 19، کشف هندسه های غیر اقلیدسی توسطنیکولای ایوانوویچ لوباچفسکی (1792-1856)، یانوس بولیای (1802-1860)، کارل فردریش گاوس (1777-1855) و دیگران منجر به احیای علاقه به این رشته شدند و در قرن بیستم، دیوید هیلبرت (186) -1943) از استدلال بدیهی در تلاش برای ارائه یک پایه مدرن از هندسه استفاده کرد.
ویژگی بارز رویکرد اقلیدس به هندسه سختی آن بود و به هندسه بدیهی یا ترکیبی معروف شد . در آغاز قرن 19، کشف هندسه های غیر اقلیدسی توسطنیکولای ایوانوویچ لوباچفسکی (1792-1856)، یانوس بولیای (1802-1860)، کارل فردریش گاوس (1777-1855) و دیگران منجر به احیای علاقه به این رشته شدند و در قرن بیستم، دیوید هیلبرت (186) -1943) از استدلال بدیهی در تلاش برای ارائه یک پایه مدرن از هندسه استفاده کرد.
اشیاء
[ویرایش]نکته ها
[ویرایش]نقاط عموماً اشیاء اساسی برای هندسه ساختمان در نظر گرفته می شوند. آنها ممکن است با خواصی که باید داشته باشند تعریف شوند، مانند تعریف اقلیدس به عنوان "آنچه که جزئی ندارد" یا در هندسه مصنوعی . در ریاضیات مدرن، آنها به طور کلی به عنوان عناصر مجموعه ای به نام فضا تعریف می شوند که خود به صورت بدیهی تعریف شده است.
با این تعاریف مدرن، هر شکل هندسی به عنوان مجموعه ای از نقاط تعریف می شود. این مورد در هندسه مصنوعی نیست، جایی که یک خط یک شی بنیادی دیگر است که به عنوان مجموعه نقاطی که از آن عبور می کند دیده نمی شود.
با این حال، هندسه های مدرنی وجود دارد که در آن نقاط، اشیاء ابتدایی یا حتی بدون نقطه نیستند. یکی از قدیمیترین این هندسهها، هندسه بدون نقطه وایتهد است که توسط آلفرد نورث وایتهد در سالهای 1919-1920 فرموله شد.
خطوط
[ویرایش]اقلیدس خطی را به عنوان "طول بی عرض" توصیف کرد که "به طور مساوی نسبت به نقاط روی خود قرار دارد". در ریاضیات مدرن، با توجه به انبوه هندسه ها، مفهوم خط با نحوه توصیف هندسه پیوند نزدیکی دارد. به عنوان مثال، در هندسه تحلیلی ، یک خط در صفحه اغلب به عنوان مجموعه نقاطی تعریف می شود که مختصات آنها معادله خطی معینی را برآورده می کند ، اما در یک محیط انتزاعی تر، مانند هندسه وقوع ، یک خط ممکن است یک شی مستقل باشد. ، متمایز از مجموعه نقاطی که روی آن قرار دارند. در هندسه دیفرانسیل، ژئودزیک تعمیم مفهوم خط بهفضاهای منحنی .
هواپیماها
[ویرایش]در هندسه اقلیدسی، صفحه یک سطح صاف و دو بعدی است که تا بی نهایت امتداد دارد. تعاریف برای انواع دیگر هندسه تعمیم آن است. صفحات در بسیاری از زمینه های هندسه استفاده می شوند. به عنوان مثال، صفحات را می توان به عنوان یک سطح توپولوژیکی بدون اشاره به فواصل یا زاویه مطالعه کرد. میتوان آن را بهعنوان یک فضای نزدیک مورد مطالعه قرار داد ، جایی که همخطیها و نسبتها را میتوان مطالعه کرد اما فاصلهها را نه. می توان آن را به عنوان صفحه مختلط با استفاده از تکنیک های تحلیل پیچیده مطالعه کرد. و غیره.
زاویه
[ویرایش]اقلیدس زاویه صفحه را به عنوان تمایل به یکدیگر، در یک صفحه، از دو خط که یکدیگر را ملاقات می کنند و نسبت به یکدیگر مستقیم نیستند، تعریف می کند. در اصطلاح امروزی، زاویه شکلی است که توسط دو پرتو تشکیل شده است ، که اضلاع زاویه نامیده میشوند و نقطه پایانی مشترکی دارند که به آن راس زاویه میگویند
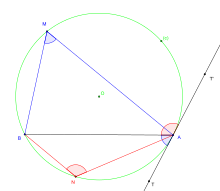
اقلیدس زاویه صفحه را به عنوان تمایل به یکدیگر، در یک صفحه، از دو خط که یکدیگر را ملاقات می کنند و نسبت به یکدیگر مستقیم نیستند، تعریف می کند. در اصطلاح امروزی، زاویه شکلی است که توسط دو پرتو تشکیل شده است ، که اضلاع زاویه نامیده میشوند و نقطه پایانی مشترکی دارند که به آن راس زاویه میگویند .
زوایای تند (الف)، مبهم (ب) و مستقیم (ج). زوایای تند و منفرد به زوایای مایل نیز معروف هستند.
در هندسه اقلیدسی ، از زاویه ها برای مطالعه چند ضلعی ها و مثلث ها و همچنین تشکیل یک شی مورد مطالعه به تنهایی استفاده می شود. مطالعه زوایای یک مثلث یا زوایای یک دایره ، اساس مثلثات را تشکیل می دهد.
در هندسه دیفرانسیل و حساب دیفرانسیل و انتگرال ، زوایای بین منحنی های صفحه یا منحنی های فضایی یا سطوح را می توان با استفاده از مشتق محاسبه کرد .
منحنی ها
[ویرایش]منحنی یک جسم 1 بعدی است که ممکن است مستقیم (مانند یک خط) باشد یا خیر. منحنی های فضای دوبعدی را منحنی های صفحه و منحنی های فضای سه بعدی را منحنی های فضایی می نامند .
در توپولوژی، منحنی با تابعی از بازه ای از اعداد واقعی تا فضای دیگر تعریف می شود. در هندسه دیفرانسیل، از همان تعریف استفاده میشود، اما تابع تعریف کننده باید قابل تمایز باشد هندسه جبری منحنیهای جبری را مطالعه میکند که به عنوان انواع جبری بعد یک تعریف میشوند.
سطح
[ویرایش]
سطح یک جسم دو بعدی است، مانند کره یا پارابولوئید. در هندسه دیفرانسیل و توپولوژی ، سطوح با «لکههای» دو بعدی (یا همسایگیها ) توصیف میشوند که به ترتیب توسط دیفرمورفیسمها یا همومورفیسمها مونتاژ میشوند . در هندسه جبری، سطوح با معادلات چند جمله ای توصیف می شوند .
منیفولدها
[ویرایش]منیفولد تعمیم مفاهیم منحنی و سطح است. در توپولوژی ، منیفولد فضای توپولوژیکی است که در آن هر نقطه دارای یک همسایگی است است که با فضای اقلیدسی همومورف است . در هندسه دیفرانسیل ، منیفولد قابل تمایز فضایی است که در آن هر همسایگی با فضای اقلیدسی تفاوت دارد.
منیفولدها به طور گسترده در فیزیک از جمله در نسبیت عام و نظریه ریسمان استفاده می شوند.
طول، مساحت و حجم
[ویرایش]طول ، مساحت و حجم به ترتیب اندازه یا وسعت یک جسم را در یک بعدی، دو بعدی و سه بعدی توصیف می کنند.
که در هندسه اقلیدسی و هندسه تحلیلی ، طول یک پاره خط را اغلب می توان با قضیه فیثاغورث محاسبه کرد .
مساحت و حجم را می توان به عنوان کمیت های اساسی جدا از طول تعریف کرد یا می توان آنها را بر حسب طول در یک صفحه یا فضای سه بعدی توصیف و محاسبه کرد. ریاضیدانان فرمول های صریح بسیاری برای مساحت و فرمول های حجم اجسام مختلف هندسی یافته اند. در حساب دیفرانسیل و انتگرال ، مساحت و حجم را می توان بر حسب انتگرال تعریف کرد ، مانند انتگرال ریمان یا انتگرال لبگ است.
معیارها و سنجش ها
[ویرایش]مفهوم طول یا فاصله را می توان تعمیم داد و به ایده متریک منجر شد. برای مثال، متریک اقلیدسی فاصله بین نقاط در صفحه اقلیدسی را اندازهگیری میکند ، در حالی که متریک هذلولی فاصله را در صفحه هذلولی اندازهگیری میکند . از دیگر نمونههای مهم معیارها میتوان به متریک لورنتز نسبیت خاص و معیارهای نیمه ریمانی نسبیت عام اشاره کرد.
در جهتی متفاوت، مفاهیم طول، مساحت و حجم توسط تئوری اندازه گیری گسترش می یابد که روش های تعیین اندازه یا اندازه را مطالعه می کند. به مجموعهها را مطالعه میکند، که در آن معیارها از قوانینی مشابه مساحت و حجم کلاسیک پیروی میکنند.
همخوانی و تشابه
[ویرایش]همخوانی و شباهت مفاهیمی هستند که توصیف می کنند زمانی که دو شکل دارای ویژگی های مشابه هستند. در هندسه اقلیدسی، از تشابه برای توصیف اشیایی استفاده میشود که شکل یکسانی دارند، در حالی که همخوانی برای توصیف اجسامی که از نظر اندازه و شکل یکسان هستند، استفاده میشود. هیلبرت ، در کار خود در مورد ایجاد یک پایه دقیق تر برای هندسه، تطابق را به عنوان یک اصطلاح تعریف نشده که ویژگی های آن با بدیهیات تعریف می شود، در نظر گرفت .
همخوانی و شباهت در هندسه تبدیل تعمیم می یابد تعمیم مییابد، که به بررسی خواص اجسام هندسی میپردازد که توسط انواع مختلف تبدیلها حفظ میشوند.
قطب نما و سازه های مستقیم
[ویرایش]هندسهسنجهای کلاسیک به ساخت اجسام هندسی که به گونهای دیگر توصیف شدهاند، توجه ویژهای داشتند. به طور کلاسیک، تنها ابزاری که در بیشتر سازههای هندسی استفاده میشود، قطبنما و راسته است. همچنین، هر ساخت و ساز باید در تعداد محدودی از مراحل تکمیل شود. با این حال، حل برخی از مشکلات به تنهایی با این ابزارها دشوار یا غیرممکن بود و ساختارهای مبتکرانه ای با استفاده از نئوسیس ، سهمی و سایر منحنی ها یا وسایل مکانیکی پیدا شد.
بعد،ابعاد،اندازه
[ویرایش]جایی که هندسه سنتی ابعاد0(یک نقطه) 1 (یک خط )، 2 ( صفحه ) و 3 (فضا) مجاز می کرد، ریاضیدانان و فیزیکدانان تقریباً دو قرن از ابعاد بالاتر استفاده کرده اند. یکی از نمونههای کاربرد ریاضی برای ابعاد بالاتر، فضای پیکربندی یک سیستم فیزیکی است که ابعادی برابر با درجههای آزادی سیستم دارد. به عنوان مثال، پیکربندی یک پیچ را می توان با پنج مختصات توصیف کرد.
در توپولوژی کلی ، مفهوم بعد از اعداد طبیعی به بعد بی نهایت ( مثلاً فضاهای هیلبرت ) و اعداد حقیقی مثبت (در هندسه فراکتال ) گسترش یافته است. در هندسه جبری ، بعد یک تنوع جبری تعدادی تعاریف ظاهراً متفاوت دریافت کرده است که همه در رایجترین موارد معادل هستند.
نقطه،خط،صفحه،فضا
[ویرایش]نقطه
[ویرایش]در هندسه کلاسیک اقلیدسی ، نقطه یک مفهوم ابتدایی است که مکان دقیقی را در فضا مدل میکند و طول، عرض یا ضخامت ندارد. در ریاضیات مدرن ، یک نقطه به طور کلی به عنصری از مجموعه ای به نام فضا اشاره دارد.نقطه یک شی صفر بعدی است که با استفاده از آن فضای یک بعدی(خط)به وجود می آید
مفهوم ابتدایی بودن به این معنی است که یک نقطه را نمی توان بر حسب اشیاء تعریف شده قبلی تعریف کرد. به این معنا که یک نقطه فقط با برخی از ویژگی ها به نام بدیهیات تعریف می شود که باید آن ها را برآورده کند. به عنوان مثال، "دقیقا یک خط وجود دارد که از دو نقطه مختلف می گذرد" .
خط
[ویرایش]خط، امتداد نقطه است.
بر اثر حرکت و امتداد یک نقطه بر صفحه در یک راستا، خط شکل میگیرد.
خط در هندسه بهمعنی اتصال یا امتداد دو نقطه-در یک راستا-بر روی سطح (صفحه) که سطح را تقسیم میکند. خط بهطور مطلق از دو جهت، بینهایت امتداد دارد. نیمخط از یک نقطه، آغاز میشود و از دیگر سو بینهایت امتداد دارد و پارهخط از هر دو سو به دو نقطه، محدود است.
در هندسهٔ اقلیدسی، خط، عبارت است از کوتاهترین مسیر بین دو نقطه که ممکن است از هر جهت بینهایت امتداد پیدا کند. از سویی پارهخط کوتاهترین مسیر بین دو نقطه است.با استفاده از خط می توان صفحه درست کرد
صفحه
[ویرایش]به طور نامحدود گسترش می یابد. صفحه آنالوگ دو بعدی یک نقطه (ابعاد صفر)، یک خط (یک بعدی) و فضای سه بعدی است . صفحات می توانند به عنوان زیرفضاهای فضایی با ابعاد بالاتر، مانند یکی از دیوارهای اتاق، بی نهایت گسترش یافته باشند، یا ممکن است به تنهایی از وجود مستقلی برخوردار شوند،
فضا
[ویرایش]فضای سه بعدی (همچنین: فضای سه بعدی ، فضای سه بعدی یا به ندرت فضای سه بعدی ) یک تنظیم هندسی است که در آن سه مقدار (به نام پارامتر ) برای تعیین موقعیت یک عنصر (یعنی نقطه ) مورد نیاز است. این معنای غیر رسمی اصطلاح بعد است.
در ریاضیات ، چند عدد از n عدد را می توان به عنوان مختصات دکارتی یک مکان در فضای اقلیدسی n بعدی درک کرد. مجموعه این n- tuples معمولا نشان داده می شودو می توان آن را در فضای اقلیدسی n بعدی شناسایی کرد. وقتی n = 3 باشد، این فاصله فراخوانی می شودفضای اقلیدسی سه بعدی (یا به سادگی فضای اقلیدسی هنگامی که زمینه واضح است). این به عنوان مدلی از جهان فیزیکی عمل می کند (زمانی که نظریه نسبیت در نظر گرفته نمی شود)، که در آن تمام ماده شناخته شده وجود دارد. در حالی که این فضا متقاعدکنندهترین و مفیدترین راه برای مدلسازی جهان آنگونه که تجربه میشود، باقی میماند، تنها نمونهای از تنوع زیادی از فضاها در سه بعدی به نام 3 منیفولد است . در این مثال کلاسیک، هنگامی که سه مقدار به اندازه گیری در جهات مختلف ( مختصات ) اشاره دارد، هر سه جهت را می توان انتخاب کرد، مشروط بر اینکه بردارهادر این جهات همه در یک فضای 2 ( صفحه ) قرار نمی گیرند. علاوه بر این، در این مورد، این سه مقدار را می توان با هر ترکیبی از سه مورد انتخاب شده از عبارات عرض / عرض ، ارتفاع / عمق و طول برچسب گذاری کرد.
تقارن
[ویرایش]قدمت موضوع تقارن در هندسه به اندازه خود علم هندسه است. اشکال متقارن مانند دایره ، چند ضلعی های منظم و جامدات افلاطونی اهمیت عمیقی برای بسیاری از فیلسوفان باستان داشتند و قبل از زمان اقلیدس به تفصیل مورد بررسی قرار گرفتند. الگوهای متقارن در طبیعت اتفاق میافتند و به صورت هنرمندانه در بسیاری از اشکال، از جمله گرافیک لئوناردو داوینچی ، ام سی اسچر ، و دیگران ارائه شدهاند. در نیمه دوم قرن 19، رابطه بین تقارن و هندسه مورد بررسی شدید قرار گرفت.برنامه ارلانگن فلیکس کلاین اعلام کرد که به معنای بسیار دقیق، تقارن، که از طریق مفهوم گروه تبدیل بیان می شود، تعیین می کند که هندسه چیست . تقارن در هندسه کلاسیک اقلیدسی با همخوانیها و حرکات صلب نشان داده میشود ، در حالی که در هندسه تصویری نقش مشابهی توسط تلاقیها ، تبدیلهای هندسی ایفا میشود که خطوط مستقیم را به خطوط مستقیم تبدیل میکنند. اما در هندسههای جدید بولیایی و لوباچفسکی، ریمان، کلیفورد و کلاین، و سوفوس لی وجود داشت.ایده کلاین برای «تعریف هندسه از طریق گروه تقارن آن » الهام گرفته شده است. هر دو تقارن گسسته و پیوسته نقش برجسته ای در هندسه دارند، اولی در توپولوژی و نظریه گروه هندسی ، دومی در نظریه دروغ و هندسه ریمانی .
نوع متفاوتی از تقارن، اصل دوگانگی در هندسه تصویری ، در میان زمینههای دیگر است. این فراپدیده را میتوان تقریباً به این صورت توصیف کرد: در هر قضیه ، نقطه مبادله با صفحه ، پیوستن به meet ، نهفته در با حاوی ، و نتیجه یک قضیه به همان اندازه درست است. شکل مشابه و نزدیک به دوگانگی بین فضای برداری و فضای دوگانه آن وجود دارد.
برنامه های کاربری
[ویرایش]هندسه در بسیاری از زمینه ها کاربرد پیدا کرده است که در زیر به برخی از آنها اشاره می شود.
هنر
[ویرایش]ریاضیات و هنر به طرق مختلفی با هم مرتبط هستند. برای مثال، تئوری پرسپکتیو نشان داد که هندسه چیزی بیش از ویژگیهای متریک شکلها دارد: پرسپکتیو منشأ هندسه تصویری است .
هنرمندان مدتهاست که از مفاهیم تناسب در طراحی استفاده میکنند. ویتروویوس یک نظریه پیچیده از تناسبات ایده آل برای پیکر انسان ایجاد کرد. این مفاهیم توسط هنرمندانی از میکل آنژ تا هنرمندان کمیک بوک مدرن استفاده و اقتباس شده است.
نسبت طلایی نسبت خاصی است که نقشی بحث برانگیز در هنر داشته است. اغلب ادعا میشود که از نظر زیباییشناختی دلپذیرترین نسبت طول است، اغلب گفته میشود که در آثار هنری معروف گنجانده شده است، اگرچه قابلاعتمادترین و بدون ابهامترین نمونهها عمداً توسط هنرمندان آگاه از این افسانه ساخته شده است.
کاشی کاری یا تزیینات در طول تاریخ در هنر استفاده شده است. هنر اسلامی مانند هنر MC Escher به طور مکرر از تسلیحات استفاده می کند . کار اشر همچنین از هندسه هذلولی استفاده کرد.
سزان این نظریه را مطرح کرد که همه تصاویر را می توان از کره ، مخروط و استوانه ساخت . این هنوز هم امروزه در تئوری هنر استفاده می شود، اگرچه فهرست دقیق اشکال از نویسنده ای به نویسنده دیگر متفاوت است.
معماری
[ویرایش]هندسه کاربردهای زیادی در معماری دارد. در واقع، گفته شده است که هندسه در هسته طراحی معماری قرار دارد. کاربردهای هندسه در معماری شامل استفاده از هندسه تصویری برای ایجاد پرسپکتیو اجباری ، استفاده از مقاطع مخروطی در ساخت گنبدها و اشیاء مشابه، استفاده از تسلسل ، و استفاده از تقارن
فیزیک
[ویرایش]حوزه نجوم ، به ویژه از آنجایی که به نقشه برداری از موقعیت ستارگان و سیارات در کره سماوی و توصیف رابطه بین حرکات اجرام سماوی مربوط می شود، به عنوان منبع مهمی از مشکلات هندسی در طول تاریخ خدمت کرده است.
هندسه ریمانی و هندسه شبه ریمانی در نسبیت عام استفاده می شود . نظریه ریسمان از چندین نوع هندسه استفاده می کند، و همچنین نظریه اطلاعات کوانتومی .
منابع
[ویرایش]- ویکی پدیای انگلیسی
آنالیز ریاضی
آنالیز ریاضی بخشهایی از ریاضیات است که با مفاهیم حد و همگرایی مربوطاند و در آنها موضوعاتی مثل پیوستگی و انتگرالگیری و مشتقپذیری و توابع غیرجبری بررسی میشود. این موضوعات را معمولاً در عرصهی اعداد حقیقی یا اعداد مختلط و توابع مربوط به آنها بحث میکنند ولی میتوان آنها را در هر فضائی از موجودات ریاضی که در آن مفهوم "نزدیکی" (فضای توپولوژیک) یا "فاصله" (فضای متریک) وجود دارد به کار برد. آنالیز ریاضی از کوششهای مربوط به دقیق کردن مبانی و تعریفهای حسابان سر برآورده است.

این نظریه ها معمولاً در زمینه اعداد و توابع حقیقی و مختلط مورد مطالعه قرار می گیرند . تجزیه و تحلیل از حساب دیفرانسیل و انتگرال ، که شامل مفاهیم اولیه و تکنیک های تجزیه و تحلیل است، تکامل یافته است. تجزیه و تحلیل را می توان از هندسه متمایز کرد . با این حال، می توان آن را برای هر فضایی از اشیاء ریاضی که تعریفی از نزدیکی (یک فضای توپولوژیکی) یا فواصل خاص بین اشیاء (یک فضای متریک) دارد، اعمال کرد.
تاریخچه
[ویرایش]ارشمیدس از روش فرسودگی برای محاسبه مساحت داخل دایره با یافتن مساحت چندضلعیهای منظم با اضلاع بیشتر و بیشتر استفاده کرد. این یک مثال اولیه اما غیررسمی از حد بود، یکی از اساسیترین مفاهیم در تجزیه و تحلیل ریاضی.
کهن
[ویرایش]تجزیه و تحلیل ریاضی به طور رسمی در قرن هفدهم در طول انقلاب علمی توسعه یافت ، اما بسیاری از ایده های آن را می توان به ریاضیدانان قبلی ردیابی کرد. نتایج اولیه در تجزیه و تحلیل به طور ضمنی در روزهای اولیه ریاضیات یونان باستان وجود داشت. به عنوان مثال، یک مجموع هندسی نامتناهی در پارادوکس زنو از دوگانگی ضمنی است . بعدها، ریاضیدانان یونانی مانند ادوکسوس و ارشمیدس زمانی که از روش فرسودگی استفاده کردند، از مفاهیم حدود و همگرایی صریح تر، اما غیررسمی استفاده کردند.برای محاسبه مساحت و حجم مناطق و جامدات. استفاده صریح از بینهایتها در روش قضایای مکانیکی ارشمیدس ، اثری که در قرن بیستم دوباره کشف شد، ظاهر میشود. در آسیا، ریاضیدان چینی لیو هوی از روش خستگی در قرن سوم پس از میلاد برای یافتن مساحت دایره استفاده کرد. از ادبیات جین، چنین به نظر می رسد که هندوها در اوایل قرن چهارم قبل از میلاد ، فرمول های جمع سری های حسابی و هندسی را در اختیار داشتند آکاریا بهدراباهو از مجموع یک سری هندسی در کالپسوترا خود در سال 433 استفاده می کند. قبل از میلاد در ریاضیات هندی ، نمونه های خاصی از سری های حسابی به طور ضمنی در ادبیات ودایی در اوایل 2000 قبل از میلاد یافت شده است.
قرون وسطی
[ویرایش]زو چونگجی روشی را ایجاد کرد که بعداً به عنوان اصل کاوالیری برای یافتن حجم یک کره در قرن پنجم نام گرفت. در قرن دوازدهم، ریاضیدان هندی بهاسکارای دوم نمونههایی از مشتقات ارائه کرد و از آنچه امروزه به عنوان قضیه رول شناخته میشود، استفاده کرد.
در قرن چهاردهم، مادهاوا از سانگاماگراما توابعی مانند سینوس ، کسینوس ، مماس و قطبی را توسعه داد که اکنون سری تیلور نامیده می شود. در کنار توسعه سری توابع مثلثاتی تیلور ، او همچنین بزرگی عبارات خطای حاصل از کوتاه کردن این سریها را تخمین زد و یک تقریب منطقی از تعدادی سری نامتناهی ارائه کرد. پیروان او در مدرسه نجوم و ریاضیات کرالا آثار او را تا قرن شانزدهم بیشتر گسترش دادند.
نوین
[ویرایش]پایه ها
[ویرایش]مبانی مدرن تجزیه و تحلیل ریاضی در قرن هفدهم اروپا پایهگذاری شد. این زمانی آغاز شد که فرما و دکارت هندسه تحلیلی را توسعه دادند، که پیشروی حساب مدرن است. روش کفایی فرما به او اجازه داد حداکثر و حداقل توابع و مماس منحنی ها را تعیین کند. انتشار دکارت از La Géométrie در سال 1637، که سیستم مختصات دکارتی را معرفی کرد ، به عنوان ایجاد تجزیه و تحلیل ریاضی در نظر گرفته می شود. چند دهه بعد بود که نیوتن و لایب نیتس به طور مستقل توسعه یافتندحساب بی نهایت کوچک ، که با محرک کار کاربردی که تا قرن 18 ادامه یافت، به مباحث تحلیلی مانند حساب تغییرات، معادلات دیفرانسیل معمولی و جزئی ، تحلیل فوریه، و توابع تولیدی تبدیل شد. در این دوره، تکنیکهای حساب دیفرانسیل و انتگرال برای تقریب مسائل گسسته توسط مسایل پیوسته استفاده شد.
نوسازیویرایش کنید
[ویرایش]در قرن هجدهم، اویلر مفهوم تابع ریاضی را معرفی کرد. زمانی که برنارد بولزانو تعریف مدرن تداوم را در سال 1816 ارائه کرد، تحلیل واقعی به عنوان یک موضوع مستقل شروع به ظهور کرد ، اما کار بولزانو تا دهه 1870 به طور گسترده ای شناخته نشد. در سال 1821، کوشی با رد اصل عمومیت جبر که به طور گسترده در کارهای قبلی، به ویژه توسط اویلر، استفاده می شد، شروع به قرار دادن حساب بر روی یک پایه منطقی محکم کرد. در عوض، کوشی حساب دیفرانسیل و انتگرال را بر اساس ایده های هندسی و بی نهایت کوچک فرموله کرد . بنابراین، تعریف او از تداوم مستلزم تغییر بی نهایت کوچک در x بودبرای مطابقت با یک تغییر بی نهایت کوچک در y . او همچنین مفهوم دنباله کوشی را معرفی کرد و نظریه رسمی تحلیل پیچیده را آغاز کرد . پواسون , لیوویل , فوریه و دیگران معادلات دیفرانسیل جزئی و آنالیز هارمونیک را مطالعه کردند . مشارکت این ریاضیدانان و دیگران، مانند وایرشتراس ، (ε، δ) -تعریف رویکرد حد را توسعه دادند، بنابراین زمینه مدرن تجزیه و تحلیل ریاضی را پایهگذاری کردند.
در اواسط قرن نوزدهم، ریمان نظریه ادغام خود را مطرح کرد . در ثلث آخر قرن، وایرشتراس ، تحلیل را حساب کرد ، که فکر میکرد استدلال هندسی ذاتاً گمراهکننده است، و تعریف «epsilon-delta» از حد را ارائه کرد. سپس، ریاضیدانان شروع به نگرانی کردند که آنها وجود زنجیره ای از اعداد واقعی را بدون اثبات فرض می کنند. سپس ددکیند اعداد واقعی را با برش های ددکیند ساخت، که در آن اعداد غیر منطقی به طور رسمی تعریف می شوند، که برای پر کردن "شکاف" بین اعداد گویا، در نتیجه یک مجموعه کامل ایجاد می کنند: زنجیره اعداد واقعی، که قبلاً توسط سیمون استوین بر حسب بسط های اعشاری ایجاد شده بود. در همان زمان، تلاشها برای اصلاح قضایای ادغام ریمان منجر به مطالعه «اندازه» مجموعه ناپیوستگیهای توابع واقعی شد.
همچنین، " هیولاها " ( هیچ جا توابع پیوسته ، توابع پیوسته اما هیچ جا قابل تمایز ، منحنی های پرکننده فضا ) شروع به بررسی کردند. در این زمینه، جردن نظریه اندازه گیری خود را توسعه داد ، کانتور آنچه را که امروزه نظریه مجموعه ساده لوح نامیده می شود ، و بایر قضیه دسته بایر را اثبات کرد . در اوایل قرن بیستم، حساب دیفرانسیل و انتگرال با استفاده از نظریه مجموعههای بدیهی رسمیت یافت . Lebesgue مشکل اندازه گیری را حل کرد و هیلبرت فضاهای هیلبرت را برای حل معرفی کردمعادلات انتگرال . ایده فضای برداری هنجاری در هوا بود، و در دهه 1920، Banach تجزیه و تحلیل عملکردی را ایجاد کرد.
مفاهیم مهم
[ویرایش]فضاهای متریک
[ویرایش]در ریاضیات ، فضای متریک مجموعهای است که در آن مفهوم فاصله (به نام متریک ) بین عناصر مجموعه تعریف میشود.
بسیاری از تحلیل ها در فضای متریک اتفاق می افتد. متداول ترین آنها عبارتند از: خط واقعی ، صفحه مختلط ، فضای اقلیدسی ، سایر فضاهای برداری و اعداد صحیح . نمونههایی از تجزیه و تحلیل بدون متریک شامل نظریه اندازهگیری (که اندازه را به جای فاصله توصیف میکند) و تحلیل عملکردی (که فضاهای برداری توپولوژیکی را که نیازی به احساس فاصله ندارند، مطالعه میکند).
به طور رسمی، یک فضای متریک یک جفت مرتب شده است(M,d) جایی کهMیک مجموعه است وdیک متریک در است، پسM یک تابع است.
به طوری که برای هر موارد زیر صادق است:
( هویت غیر قابل تشخیص ها) ( تقارن ) ( نابرابری مثلث ) با گرفتن ملک سوم و اجاره، می توان نشان داد که ( غیر منفی ).
توالی ها و محدودیت
[ویرایش]دنباله یک لیست مرتب شده است. مانند یک مجموعه ، شامل اعضایی است (که عناصر یا اصطلاحات نیز نامیده می شوند ). برخلاف یک مجموعه، نظم مهم است و دقیقاً همان عناصر می توانند چندین بار در موقعیت های مختلف دنباله ظاهر شوند. به طور دقیق تر، یک دنباله را می توان به عنوان تابعی تعریف کرد که دامنه آن یک مجموعه کاملاً مرتب قابل شمارش است، مانند اعداد طبیعی .
یکی از مهمترین ویژگی های یک دنباله همگرایی است . به طور غیررسمی، یک دنباله اگر حدی داشته باشد همگرا می شود . در ادامه غیررسمی، یک دنباله ( منفرد-بی نهایت ) اگر به نقطه x نزدیک شود که حد نامیده می شود، محدودیتی دارد، زیرا n بسیار بزرگ می شود. یعنی برای یک دنباله انتزاعی ( a n ) (که n از 1 تا بی نهایت قابل درک است) فاصله بین a n و x به 0 نزدیک می شود که n → ∞ نشان داده شده است.
شاخه های اصلی
[ویرایش]تحلیل واقعی
[ویرایش]تحلیل واقعی (به طور سنتی، نظریه توابع یک متغیر واقعی ) شاخه ای از تحلیل ریاضی است که با اعداد واقعی و توابع با ارزش واقعی یک متغیر واقعی سروکار دارد. به طور خاص، به ویژگی های تحلیلی توابع و دنباله های واقعی ، از جمله همگرایی و حدود دنباله های اعداد حقیقی، حساب اعداد حقیقی، و تداوم ، همواری و ویژگی های مرتبط توابع با ارزش واقعی می پردازد . .
تحلیل پیچیده
[ویرایش]تجزیه و تحلیل مختلط (به طور سنتی به عنوان نظریه توابع یک متغیر مختلط شناخته می شود) شاخه ای از تجزیه و تحلیل ریاضی است که به بررسی توابع اعداد مختلط می پردازد. در بسیاری از شاخه های ریاضیات، از جمله هندسه جبری ، نظریه اعداد ، ریاضیات کاربردی مفید است . و همچنین در فیزیک ، از جمله هیدرودینامیک ، ترمودینامیک ، مهندسی مکانیک ، مهندسی برق ، و به ویژه، نظریه میدان کوانتومی .
تحلیل پیچیده به ویژه با توابع تحلیلی متغیرهای پیچیده (یا به طور کلی تر، توابع مرومورفیک ) سروکار دارد. از آنجایی که بخش های واقعی و خیالی مجزای هر تابع تحلیلی باید معادله لاپلاس را برآورده کند ، تحلیل پیچیده به طور گسترده برای مسائل دو بعدی در فیزیک قابل استفاده است .
تجزیه و تحلیل عملکردو
[ویرایش]آنالیز تابعی شاخه ای از تحلیل ریاضی است که هسته آن با مطالعه فضاهای برداری که دارای نوعی ساختار مرتبط با حد هستند (مثلاً حاصل ضرب درونی ، هنجار ، توپولوژی و غیره) و عملگرهای خطی بر روی این فضاها تشکیل می شود و احترام به این ساختارها به معنای مناسب. ریشه های تاریخی تحلیل تابعی در مطالعه فضاهای توابع و فرمول بندی ویژگی های تبدیل توابع مانند تبدیل فوریه به عنوان تبدیل هایی است که پیوسته و واحد را تعریف می کنند.و غیره عملگرهای بین فضاهای تابع. این دیدگاه مشخص شد که برای مطالعه معادلات دیفرانسیل و انتگرال مفید است.
تحلیل هارمونیک
[ویرایش]آنالیز هارمونیک شاخه ای از آنالیز ریاضی است که به نمایش توابع و سیگنال ها به عنوان برهم نهی امواج اساسی می پردازد. این شامل مطالعه مفاهیم سری فوریه و تبدیل فوریه ( تحلیل فوریه ) و تعمیم آنها است. تجزیه و تحلیل هارمونیک در زمینه های مختلفی مانند تئوری موسیقی ، نظریه اعداد ، نظریه نمایش ، پردازش سیگنال ، مکانیک کوانتومی ، تجزیه و تحلیل جزر و مد و علوم اعصاب کاربرد دارد.
معادلات دیفرانسیل
[ویرایش]معادله دیفرانسیل یک معادله ریاضی برای یک تابع مجهول از یک یا چند متغیر است که مقادیر خود تابع و مشتقات آن از مرتبه های مختلف را به هم مرتبط می کند. معادلات دیفرانسیل نقش برجسته ای در مهندسی ، فیزیک ، اقتصاد ، زیست شناسی و سایر رشته ها ایفا می کنند.
معادلات دیفرانسیل در بسیاری از حوزههای علم و فناوری به وجود میآیند، بهویژه زمانی که یک رابطه قطعی شامل مقادیری پیوسته متغیر (مدلسازی شده با توابع) و نرخهای تغییر آنها در مکان یا زمان (بیان شده به عنوان مشتقات) شناخته یا فرض شود. این در مکانیک کلاسیک نشان داده شده است ، جایی که حرکت یک جسم با موقعیت و سرعت آن با تغییر مقدار زمان توصیف میشود. قوانین نیوتن به شخص اجازه می دهد (با توجه به موقعیت، سرعت، شتاب و نیروهای مختلف وارد بر جسم) این متغیرها را به صورت دینامیکی به عنوان یک معادله دیفرانسیل برای موقعیت مجهول جسم به عنوان تابعی از زمان بیان کند. در برخی موارد، این معادله دیفرانسیل (که معادله حرکت نامیده می شود) ممکن است به صراحت حل شود.
تئوری اندازه گیری
[ویرایش]اندازه گیری در یک مجموعه روشی سیستماتیک برای اختصاص یک عدد به هر زیر مجموعه مناسب از آن مجموعه است که به طور شهودی به عنوان اندازه آن تفسیر می شود. در این معنا، معیار تعمیم مفاهیم طول، مساحت و حجم است. یک مثال مهم، اندازه گیری Lebesgue در فضای اقلیدسی است که طول ، مساحت و حجم معمولی هندسه اقلیدسی را به زیرمجموعه های مناسب نسبت می دهد.فضای اقلیدسی بعدی. به عنوان مثال، اندازه گیری Lebesgue از فاصله در اعداد واقعی طول آن به معنای روزمره کلمه است - به طور خاص، 1.
از نظر فنی، یک اندازه گیری تابعی است که یک عدد واقعی غیر منفی یا +∞ را به زیرمجموعه های (بعضی) یک مجموعه اختصاص می دهد.. باید 0 را به مجموعه خالی اختصاص دهد و ( قابل شمارش ) جمعی باشد: اندازه یک زیر مجموعه "بزرگ" که می تواند به تعداد محدود (یا قابل شمارش) از زیر مجموعه های ناهمگون "کوچکتر" تجزیه شود، مجموع مقادیر زیر مجموعه های "کوچکتر". به طور کلی، اگر کسی بخواهد یک اندازه ثابت را به هر زیر مجموعه از یک مجموعه معین مرتبط کند و در عین حال سایر بدیهیات یک اندازه گیری را برآورده کند، فقط نمونه های بی اهمیتی مانند معیار شمارش را پیدا می کند . این مشکل با تعریف اندازه گیری فقط در زیر مجموعه ای از همه زیر مجموعه ها حل شد. به اصطلاح زیر مجموعه های قابل اندازه گیری که برای تشکیل الف مورد نیاز است-جبر . این بدان معنی است که اتحادیه های قابل شمارش، تقاطع های قابل شمارش و مکمل های زیر مجموعه های قابل اندازه گیری قابل اندازه گیری هستند. مجموعههای غیرقابل اندازهگیری در فضای اقلیدسی، که معیار لبگ را نمیتوان بهطور پیوسته بر اساس آنها تعریف کرد، لزوماً به این معنا که به شدت با مکملشان مخلوط میشوند، پیچیده هستند. در واقع، وجود آنها پیامد غیر پیش پا افتاده اصل انتخاب است.
تحلیل عددی
[ویرایش]تحلیل عددی مطالعه الگوریتمهایی است که از تقریب عددی (برخلاف دستکاریهای نمادین عمومی ) برای مسائل آنالیز ریاضی (که از ریاضیات گسسته متمایز میشوند ) استفاده میکنند.
تجزیه و تحلیل عددی مدرن به دنبال پاسخ های دقیق نیست، زیرا اغلب به دست آوردن پاسخ های دقیق در عمل غیرممکن است. در عوض، بسیاری از تحلیلهای عددی به دستیابی به راهحلهای تقریبی و در عین حال حفظ مرزهای منطقی در خطاها مربوط میشود.
تجزیه و تحلیل عددی به طور طبیعی در همه زمینه های مهندسی و علوم فیزیکی کاربرد دارد، اما در قرن بیست و یکم، علوم زیستی و حتی هنرها عناصر محاسبات علمی را به کار گرفته اند. معادلات دیفرانسیل معمولی در مکانیک سماوی (سیاره ها، ستاره ها و کهکشان ها) ظاهر می شوند. جبر خطی عددی برای تجزیه و تحلیل داده ها مهم است. معادلات دیفرانسیل تصادفی و زنجیره های مارکوف در شبیه سازی سلول های زنده برای پزشکی و زیست شناسی ضروری هستند.
تحلیل برداری
[ویرایش]آنالیز برداری شاخه ای از آنالیز ریاضی است که با مقادیری که هم اندازه و هم جهت دارند سروکار دارد. برخی از نمونه های بردار عبارتند از سرعت، نیرو و جابجایی. بردارها معمولاً با اسکالرها همراه هستند، مقادیری که بزرگی را توصیف می کنند.
تحلیل اسکالر
[ویرایش]آنالیز اسکالر شاخهای از تحلیل ریاضی است که با مقادیر مربوط به مقیاس بر خلاف جهت سروکار دارد. مقادیری مانند دما اسکالر هستند زیرا بزرگی یک مقدار را بدون توجه به جهت، نیرو یا جابجایی که مقدار ممکن است داشته باشد یا نداشته باشد، توصیف می کنند.
منابع
[ویرایش]ویکی پدیای فارسی[۱]
ویکی پدیای انگلیسی[۲]
آمار و احتمال
آمار و احتمال دو مبحثی از ریاضیات هستند که از مفاهیم گسسته هستند و درمورد شانس ها، محاسبات نموداری و... می پردازد
تعریف آمار
[ویرایش]آمار (در ایران) (به انگلیسی: Statistics) (به فرانسوی: Statistiques) یا احصائیه (در افغانستان) شاخهای از ریاضیات است که به گردآوری، تحلیل، و ارائه دادهها میپردازد. آمار را باید علم استخراج و توسعهٔ دانشهای تجربی انسانی با استفاده از روشهای گردآوری و تحلیل دادههای تجربی (حاصل از اندازهگیری و آزمایش) دانست. روشهای محاسباتی جدیدتر توسط رایانه همچون یادگیری ماشینی، و کاوشهای ماشینی در دادهها، در واقع، امتداد و گسترش دانش آمار به عهد محاسبات نو و دوران اعمال شیوههای ماشینی بوده و امروزه علم آمار را به علم بیان علوم دیگر مبدل ساختهاست.
در صورتی که شاخهای علمی مد نظر نباشد، معنای آن، دادههایی بهشکل ارقام و اعداد واقعی یا تقریبی است که با استفاده از علم آمار میتوان با آنها رفتار کرد و عملیات ذکر شده در بالا را بر آنها انجام داد. بیشتر مردم با کلمه آمار به مفهومی که برای ثبت و نمایش اطلاعات عددی به کار میرود آشنا هستند؛ ولی این مفهوم منطبق با موضوع اصلی مورد بحث آمار نیست. آمار عمدتاً با وضعیتهایی سر و کار دارد که در آنها وقوع یک پیشامد بهطور حتمی قابل پیشبینی نیست. اسنتاجهای آماری غالباً غیر حتمی اند، زیرا مبتنی بر اطلاعات ناکاملی هستند. در طول چندین دهه آمار فقط با بیان اطلاعات و مقادیر عددی دربارهٔ اقتصاد و جمعیتشناسی در یک کشور سر و کار داشت. حتی امروز بسیاری از نشریات و گزارشهای دولتی که تودهای از آمار و ارقام را دربردارند معنی اولیه کلمه آمار را در ذهن زنده میکنند. اکثر افراد معمولی هنوز این تصویر غلط را دربارهٔ آمار دارند که آن را منحصر به ستونهای عددی سرگیجهآور و اشکال مبهوتکننده میدانند؛ بنابراین، یادآوری این نکته ضروری است که نظریه و روشهای جدید آماری از حد ساختن جدولهای اعداد و نمودارها بسیار فراتر رفتهاند. آمار به عنوان یک موضوع علمی، امروزه شامل مفاهیم و روشهایی است که در تمام پژوهشهایی که مستلزم جمعآوری دادهها به وسیله یک فرایند آزمایش و مشاهده و انجام استنباط و نتیجهگیری به وسیله تجزیه و تحلیل این دادهها هستند اهمیت بسیار دارند.
علم آمار
[ویرایش]علم آمار، مبتنی است بر دو شاخه آمار توصیفی و آمار استنباطی. در آمار توصیفی با داشتن تمام اعضا جامعه به بررسی خصوصیتهای آماری آن پرداخته میشود در حالی که در آمار استنباطی با بدست آوردن نمونهای از جامعه که خصوصیات اصلی جامعه را بیان میکند در مورد جامعه استباط آماری انجام میشود. در نظریهٔ آمار، اتفاقات تصادفی و عدم قطعیت توسط نظریهٔ احتمالات مدلسازی میشوند. در این علم، مطالعه و قضاوت معقول در بارهٔ موضوعهای گوناگون، بر مبنای یک نمونه انجام میشود و قضاوت در مورد یک فرد خاص، اصلاً مطرح نیست.
از جملهٔ مهمترین اهداف آمار، میتوان تولید «بهترین» اطّلاعات از دادههای موجود و سپس استخراج دانش از آن اطّلاعات را ذکر کرد. به همین سبب است که برخی از منابع، آمار را شاخهای از نظریه تصمیمها بهشمار میآورند.
از طرف دیگر میتوان آن را به دو بخش آمار کلاسیک و آمار بیز (Bayesian) تقسیمبندی کرد. در آمار کلاسیک، ابتدا آزمایش و نتیجه را داریم و بعد بر اساس آنها فرضها را آزمون میکنیم. به عبارت دیگر ابتدا آزمایش انجام میشود و بعد فرض آزمون میگردد. در آمار بیزی ابتدا فرض در نظر گرفته میشود و دادهها با آن مطابقت داده میشوند به عبارت دیگر در آمار بیزی یک پیش داریم-توزیع پیشین- و بعد از مطالعه دادهها و برای رسیدن به آن توزیع پیشین، توزیع پسین را در نظر میگیریم.
علم آمار یکی از علوم مرتبط با علم دادهها است.
تاریخ
[ویرایش]بحث های رسمی در مورد استنتاج به ریاضیدانان و رمزنگاران عرب ، در دوران طلایی اسلامی بین قرن های 8 و 13 باز می گردد . الخلیل (717-786) کتاب پیام های رمزی را نوشت که شامل یکی از اولین کاربردهای جابجایی و ترکیب است تا همه کلمات ممکن عربی را با و بدون مصوت فهرست کند. [15] کتاب خطی الکندی در مورد رمزگشایی پیام های رمزنگاری شده شرح مفصلی از نحوه استفاده از تجزیه و تحلیل فرکانس برای رمزگشایی پیام های رمزگذاری شده ارائه می دهد و نمونه اولیه ای از استنتاج آماری برای رمزگشایی ابن عدلان (1187-1268) بعدها سهم مهمی در استفاده از اندازه نمونه در تحلیل بسامدی داشت.
کاربردهای اولیه تفکر آماری حول نیاز دولتها برای استناد به سیاستها بر اساس دادههای جمعیتشناختی و اقتصادی بود، از این رو ریشهشناسی آن . دامنه رشته آمار در اوایل قرن 19 گسترش یافت و شامل جمع آوری و تجزیه و تحلیل داده ها به طور کلی شد. امروزه آمار به طور گسترده در دولت، تجارت و علوم طبیعی و اجتماعی به کار گرفته می شود.
مبانی ریاضی آمار از بحث های مربوط به بازی های شانسی در بین ریاضیدانانی مانند جرولامو کاردانو ، بلز پاسکال ، پیر دو فرما ، و کریستیان هویگنس ایجاد شد . اگرچه ایده احتمال قبلاً در حقوق و فلسفه باستان و قرون وسطی (مانند کار خوان کاراموئل ) بررسی شده بود، نظریه احتمال به عنوان یک رشته ریاضی تنها در اواخر قرن هفدهم شکل گرفت، به ویژه در اثر پس از مرگ یاکوب برنولی Ars . کنجکتندی .این اولین کتابی بود که در آن قلمرو بازیهای شانس و قلمرو احتمالات (که مربوط به نظر، شواهد و استدلال بود) با هم ترکیب شدند و به تحلیل ریاضی ارائه شدند.روش حداقل مربعات برای اولین بار توسط آدرین ماری لژاندر در سال 1805 توصیف شد ، اگرچه کارل فردریش گاوس احتمالاً یک دهه قبل از آن در سال 1795 از آن استفاده کرد.
تعریف احتمال
[ویرایش]بهطور ساده، احتمالات (به انگلیسی: Probability) به شانس وقوع یک حادثه گفته میشود.
احتمال معمولاً مورد استفاده برای توصیف نگرش ذهن نسبت به گزارههایی است که ما از حقیقت آنها مطمئن نیستیم. گزارههای مورد نظر معمولاً از فرم "آیا یک رویداد خاص رخ میدهد؟" و نگرش ذهن ما از فرم "چقدر اطمینان داریم که این رویداد رخ خواهد داد؟" است. میزان اطمینان ما، قابل توصیف به صورت عددی میباشد که این عدد مقداری بین ۰ و ۱ را گرفته و آن را احتمال می نامیم. هر چه احتمال یک رویداد بیشتر باشد، ما مطمئن تر خواهیم بود که آن رویداد رخ خواهد داد. در واقع میزان اطمینان ما از اینکه یک واقعه (تصادفی) اتفاق خواهد افتاد.
نظریهٔ احتمالات
[ویرایش]نظریهٔ احتمالات به شاخهای از ریاضیات گویند که با تحلیل وقایع تصادفی سروکار دارد.
مانند دیگر نظریهها، نظریه احتمال نمایشی از مفاهیم احتمال به صورت شرایط صوری (فرمولی) است – شرایطی که میتواند بهطور جدا از معنای خود در نظر گرفته شود. این فرمولبندی صوری توسط قوانین ریاضی و منطق دستکاری، و نتیجههای حاصله، تفسیر یا دوباره به دامنه مسئله ترجمه میشوند.
حداقل دو تلاش موفق برای به صورت فرمول درآوردن احتمال وجود دارد: فرمولاسیون کولموگروف و فرمولاسیون کاکس. در فرمولاسیون کولموگروف (نگاه کنیدبه)، مجموعهها به عنوان واقعه و احتمالات را به عنوان میزانی روی یک سری از مجموعهها تفسیر میکنند. در نظریه کاکس، احتمال به عنوان یک اصل (که هست، بدون تجزیه و تحلیل بیشتر) و تأکید بر روی ساخت یک انتساب سازگار از مقادیر احتمال برای گزارهها است. در هر دو مورد، قوانین احتمال یکی هستند مگر برای جزئیات تکنیکی مربوط به آنها.
روشهای دیگری نیز برای کمیکردن میزان عدم قطعیت، مانند نظریه Dempster-Shafer theory یا possibility theory وجود دارد، اما آنها بهطور اساسی با آنچه گفته شد، تفاوت دارند و با درک معمول از قوانین احتمال سازگار نیستند.
پیشینه
[ویرایش]نخستین کتابها را دو دانشمند ایتالیایی دربارهٔ بازی با تاس نوشتند: جه رولاموکاردان و گالیلئو گالیله. با این همه باید آغاز بحث دقیق دربارهٔ احتمال را سده هفدهم و با کارهای بلز پاسکال و پیر فرما، ریاضیدانان فرانسوی و کریستین هویگنس هلندی دانست. پاسکال و فرما کتابی در این باره ننوشتند و تنها در نامههای خود به دیگران دربارهٔ کاربرد آنالیز ترکیبی در مسئلههای مربوط به شانس صحبت کردهاند، ولی هویگنس کتابی با نام بازی با تاس نوشت که اگر چه با کتاب کاردان هم نام است ولی از نظر تحلیل علمی در سطح بسیار بالاتری است. کار آنان توسط یاکوب برنولی و دموآور در قرن هجدهم میلادی ادامه یافت، برنولی کتاب روش حدس زدن را نوشت و قانون عددهای بزرگ را کشف کرد. مسئله معروف سوزن نیز در اواسط همین قرن توسط کنت دو بوفون مطرح و حل شد. در سده هجدهم و ابتدای سده نوزدهم نظریه احتمال در دانشهای طبیعی و صنعت بهطور جدی کاربرد پیدا کرد. در این دوره نخستین قضیههای نظریه احتمال یعنی قضایای لاپلاس، پواسون، لژاندر و گاوس ثابت شد. در نیمه دوم سده نوزدهم دانشمندان روسی تأثیر زیادی در پیشرفت نظریه احتمال داشتند، چبیشف و شاگردانش، لیاپونوف و مارکوف یک رشته از مسئلههای کلی نظریه احتمال را حل کردند و قضایای برنولی و لاپلاس را تعمیم دادند. در آغاز قرن بیستم متخصصان کارهای قبلی را منظم نموده و ساختمان اصول موضوعه احتمال را بنا نمودند. در این دوره دانشمندان زیادی روی نظریه احتمال کار کردند: در فرانسه، بورل، لهوی و فرهشه؛ در آلمان، میزس؛ در آمریکا، وینر، فه لر و دوب؛ در سوئد، کرامر؛ در شوروی، خین چین، سلوتسکی، رومانوسکی، سمپرنوف، گنه دنکو اما درخشانترین نام در این عرصه کولموگروف روسی است که اصول موضوع احتمال را در کتابی به نام مبانی نظریه احتمال در آلمان منتشر کرد.
مبانی
[ویرایش]آزمایشی را در نظر بگیرید که اجرای تکراری آن میتواند نتایج متفاوتی را ایجاد کند. مجموعه تمام نتایج ممکن برای چنین آزمایشی را به عنوان «فضای نمونه» (Sample Space) آزمایش تصادفی میشناسیم. «مجموعه توانی» (Power Set) حاصل از فضای نمونه یا معادل آن، «فضای پیشامد» (Event Space) با در نظر گرفتن کلیه مجموعههای مختلف از فضای نمونه، شکل میگیرد.
منابع
[ویرایش]ویکی پدیای فارسی
نظریه مجموعهها
نظریه مجموعهها شاخهای از منطق ریاضی است که به مطالعه مجموعهها میپردازد. مجموعهها، گردایهای از اشیاء هستند. هر چند هر نوعی از اشیاء میتوانند یک مجموعه را تشکیل دهند، اما نظریه مجموعهها اغلب در مورد اشیاء مرتبط با ریاضی به کار میرود. زبان نظریه مجموعهها را میتوان در تعریف تقریباً همهی اشیاء ریاضی به کار برد.
مطالعه جدید بر روی نظریه مجموعهها توسط گئورگ کانتور و ریچارد ددکیند در دهه ۷۰ قرن ۱۸ میلادی آغاز شد. پس از کشف تناقضهای نظریه طبیعی مجموعهها، دستگاههای اصل موضوعی بیشماری در اوایل سده ۲۰ مطرح شدند که معروفترین آنها اصل موضوعه زرملو-فرانکل و اصل موضوعه انتخاب هستند. نظریه مجموعهها عموماً به عنوان سیستم بنیادین ریاضیات در شکل نظریه مجموعههای زرملو-فرانکل همراه با اصل موضوعه انتخاب به کار میرود. گذشته از نقش بنیادین آن، نظریه مجموعهها در جایگاه خود یکی از شاخههای ریاضی با جامعه پژوهش فعالی محسوب میشود. پژوهشهای معاصر در نظریه مجموعهها موضوعهای متنوعی را شامل میشود که از ساختار خط اعداد حقیقی تا مطالعه سازگاری اعداد بزرگ متغیر است.
اجتماع
[ویرایش]اجتماع در ریاضی به معنای این است که دو زیر مجموعه را تمامی عضوهاو عناصر آن دو زیرمجموعه (مثلAوB)را نشان میدهد. اجتماع با نمادنشان داده می شود.
اصول اجتماع
[ویرایش]مجموعه های A و S داریم. اگر S مجموعه ای از مجموعه های نظری (S یک رده در مجموعه ها باشد) مجموعه ای به اسم مجموعه C بدست می آید که مجموعه و عناصر و اعضای Sزیر مجموعه آن باشد. اگرباشد پس مجموعه A اینگونه است. اجتماع همه اعضای S که آن را با یا نشان میدهیم بهصورت زیر تعریف می میشود:

خواص اجتماع
[ویرایش]اجتماع دارای اصولی است
مجموعهبامجموعهبرابر است
اگر دومجموعه همسان اجتماع پیدا کنند برابر با خود آنها می شود.
اگر مجموعه تهی و یک مجموعهAاجتماع پیدا کنند برابر با مجموعهAاست
اگر مجموعهA,B,Cداشته باشیم،اشتراک اجتماع آنها را بدست آوریم به این حالت می نویسیم
یا
اشتراک
[ویرایش]اشتراک در ریاضی به معنای این است که زیر مجموعه ای مشترک دو مجموعه باشد. اجتماع را با نماد نشان میدهند.

اصول اشتراک
[ویرایش]اگر S مجموعهای ناتهی از مجموعهها باشد و عضو دلخواهی از S، اشتراک همه اعضای S که آنرا با یا نشان میدهیم بهصورت زیر تعریف میشود:
منابع
[ویرایش]- ویکی پدیای فارسی
- ویکی پدیای انگلیسی
نظریه اعداد
نظریه اعداد (یا محاسبات یا محاسبات بالاتر در کاربردهای قدیمی تر) شاخه ای از ریاضیات محض است که عمدتاً به مطالعه اعداد صحیح و توابع با مقدار صحیح اختصاص دارد .اعداد صحیح را میتوان به خودی خود یا به عنوان جواب معادلات (در هندسه سیالهای) در نظر گرفت. سوالات حوزهٔ نظریه اعداد اغلب از طریق مطالعه بر روی اشیاء تحلیلی (به عنوان مثال تابع زتای ریمان) بهتر فهمیده میشوند. میتوان اعداد حقیقی را با کمک اعداد گویا مطالعه کرد، به عنوان مثال با تقریب زدن به کمک اعداد گویا (تقریب سیالهای).
اصطلاح قدیمی برای نظریه اعداد، حساب بود. اوایل سده بیستم، عبارت «نظریه اعداد» جایگزین آن شد. (واژه «حساب» نزد عوام به عنوان «محاسبات مقدماتی» پنداشته میشود. همچنین این اصطلاح در منطق ریاضیات به معنای حساب پئانو و در علوم رایانه به معنای حساب ممیز شناور میباشد) استفاده از اصطلاح حساب برای نظریه اعداد در نیمه دوم سده بیستم رواج پیدا کرد، ادعا میشود که ترویج آن تحت تأثیر فرانسویها بودهاست. بهخصوص، اصطلاح حسابی به عنوان یک صفت نسبت به نظریه اعدادی ترجیح داده میشود.
نظریه گاوس
[ویرایش]«ریاضیات ملکهٔ علوم است، و نظریهٔ اعداد ملکه ریاضیات.» نظریه اعداد دانان به مطالعه اعداد اول و همچنین خواص اشیائی که از اعداد ساخته میشوند میپردازند، (به عنوان مثال اعداد گویا) یا تعمیمهایی از اعداد تعریف میکنند (مثل اعداد صحیح جبری).
تاریخچه
[ویرایش]منشأ پیدایش
[ویرایش]طلوع حساب
[ویرایش]
قدیمیترین یافتههایی که ماهیت حساب دارند، تکهای از لوح پلیمپتون ۳۲۲ است (لارسا، مزوپتامیا، حدود ۱۸۰۰ پیش از میلاد)، که شامل فهرستی از «سهتاییهای فیثاغورثی» میباشد، یعنی اعداد صحیح ، چنانکه . این سهتاییها، بسیار زیاد و بزرگ اند، به گونه ای که تصور یافته شدنشان به روش بروت فورس (یا اثبات با افنا، با روش افنا اشتباه نشود) برای آن دوره سخت است. این لوح چنین عنوانی دارد: «تاکیلتوم قطری، که از عرض کم شده …»
طرح لوح نشان میدهد که به این لوح به زبان مدرن به این فرمول اشاره کرده:
که بهطور ضمنی در تمارین بابلیان باستان آورده شده. اگر از روش دیگری استفاده میشد، سه تاییها ابتدا ساخته شده و سپس برحسب مرتب میشدند، تا احتمالاً در کاربردهای عملی به عنوان «جدول» مورد استفاده قرار گیرند.
نظریه ها
[ویرایش]نظریه ابتدایی
[ویرایش]در نظریه مقدماتی اعداد، اعداد صحیح را بی استفاده از روشهای بهکار رفته در سایر شاخههای ریاضی بررسی میکنند. مسائل بخش پذیری، الگوریتم اقلیدس برای محاسبه بزرگترین مقسومعلیه مشترک (ب.م. م)، تجزیه اعداد به اعداد اول، جستجوی عدد کامل (به انگلیسی: perfect number) و همنهشتیها در این رده هستند. برخی از یافتههای مهم این رشته قضیه کوچک فرما، قضیه اعداد اول و قضیه اویلر، قضیه باقیمانده چینی و قانون تقابل درجه دوم هستند. خواص توابع ضربی مانند تابع موبیوس و تابع φ اویلر و دنباله اعداد صحیح و فاکتوریلها و اعداد فیبوناچی در همین حوزه قرار دارند.
حل بسیاری از مسائل در نظریه مقدماتی اعداد بر خلاف ظاهر ساده آنها نیازمند کوشش بسیار و بهکار گرفتن روشهای نوین است. چند نمونه:
- حدس گلدباخ در مورد نمایش اعداد زوج به صورت جمع دو عدد اول،
- حدس کاتالان در مورد توانهای متوالی از اعداد صحیح،
- حدس اعداد اول تؤامان در مورد بینهایت بودن زوجهای اعداد اول،
- حدس کولاتز در مورد تکرار ساده،
- حدس اعداد اول مرسن در مورد بینهایت بودن اعداد اول مرسن و …
همچنین ثابت شده که نظریه معادلات دیوفانتی تعمیمناپذیر است (به مسئله دهم هیلبرت مراجعه کنید).
نظریه تحلیلی
[ویرایش]در نظریه تحلیلی اعداد از حسابان و آنالیز مختلط برای بررسی سؤالاتی در مورد اعداد صحیح استفاده میشود. مثالهایی در این مورد قضیه اعداد اول و حدس ریمان هستند. مسئله وارینگ (یعنی نمایش هر عدد صحیح به صورت جمع چند مربع یا مکعب)، حدس اعداد اول تؤامان (یافتن بینهایت عدد اول با اختلاف ۲)، و حدس گلدباخ (نمایش هر عدد زوج بهصورت مجموع دو عدد اول) نیز با روشهای تحلیلی مورد حمله قرار گرفتهاند. اثبات متعالی (ترافرازنده) بودن ثابتهای ریاضی مانند π و e نیز در بخش نظریه تحلیلی اعداد قرار دارند. اگرچه حکمهایی در مورد اعداد ترافرازنده خارج از محدوده مطالعات اعداد صحیح به نظر میآید، در واقع مقادیر ممکن برای چندجملهایها با ضریبهای صحیح مانند e را بررسی میکنند. همچنین اینگونه مسائل با مبحث تقریب دیوفانتین نیز ارتباط نزدیک دارند که موضوع آن این است که چگونه میتوان یک عدد حقیقی داده شده را با یک عدد گویا تقریب زد؟
نظریه جبری
[ویرایش]در نظریه جبری اعداد، مفهوم عدد به اعداد جبری، که همان ریشههای چندجملهایهایی با ضریب گویا هستند، گسترش مییابد. در این حوزه اعدادی مشابه اعداد صحیح با نام اعداد صحیح جبری وجود دارد. در این عرصه لازم نیست ویژگیهای آشنای اعداد صحیح (مانند تجزیه یگانه) برقرار باشد. مزیت روشهای استفاده شده در این رشته (مثل نظریه گالوا، میدان همانستگی، نظریه رده میدان، نمایشهای گروهها و توابع-L) این است که برای این رده از اعداد، نظم را تا حدودی تأمین میکند.
نظریه هندسی
[ویرایش]نظریه هندسی اعداد (که قبلاً به آن هندسه اعداد میگفتند) جنبههایی از هندسه را به نظریه اعداد پیوند میدهد؛ و از قضیه مینکوفسکی در ارتباط با نقاط توری در مجموعههای محدب و تحقیق در مورد چپاندن کرهها در فضای Rn شروع میشود.
نظریه احتمالی
[ویرایش]بسیاری از نظریه اعداد احتمالاتی را می توان به عنوان یک مورد خاص مهم در مطالعه متغیرهایی دانست که تقریباً، اما نه کاملاً مستقل از یکدیگر هستند. به عنوان مثال، رویدادی که یک عدد صحیح تصادفی بین یک و یک میلیون بر دو بخش پذیر باشد و رویدادی که بر سه بخش پذیر باشد تقریباً مستقل هستند، اما نه کاملاً.
گاهی اوقات گفته می شود که ترکیبات احتمالی از این واقعیت استفاده می کند که هر اتفاقی با احتمال بیشتر ازگاهی باید اتفاق بیفتد می توان با عدالت برابر گفت که بسیاری از کاربردهای نظریه اعداد احتمالی به این واقعیت بستگی دارد که هر چیزی که غیرعادی باشد باید نادر باشد. اگر بتوان اشیاء جبری معینی (مثلاً راهحلهای منطقی یا صحیح برای معادلات معین) را در انتها توزیعهای معقول معینی نشان داد، نتیجه میشود که باید تعداد کمی از آنها وجود داشته باشد. این یک گزاره غیر احتمالی بسیار ملموس است که از یک گزاره احتمالی پیروی می کند.
گاهی اوقات، یک رویکرد غیر دقیق و احتمالاتی منجر به تعدادی از الگوریتم های اکتشافی و مشکلات باز می شود، به ویژه حدس کرامر .
نظریه ترکیبیاتی
[ویرایش]نظریه ترکیبیاتی اعداد به مسائلی در نظریه اعداد میپردازد که با روشهای ترکیبیاتی بررسی میشوند. پل اردوش بنیانگذار اصلی این شاخه از نظریه اعداد بود. الگوریتمهای سریع برای امتحان اعداد اول و تجزیه اعداد صحیح در رمزنگاری کاربردهای مهمی دارند.
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
ترکیبیات
ترکیبیات شاخه ای از علم ریاضیات است که عمدتاً به شمارش، هم به عنوان وسیله و هم به عنوان هدف برای به دست آوردن نتایج، و خواص معین ساختارهای محدود مربوط میشود . ارتباط نزدیکی با بسیاری از حوزه های دیگر ریاضیات دارد و کاربردهای زیادی از منطق گرفته تا فیزیک آماری و از زیست شناسی تکاملی تا علوم کامپیوتر دارد .
دامنه کامل ترکیبیات مورد توافق جهانی قرار نگرفته است. به گفته HJ Ryser ، تعریف موضوع دشوار است زیرا از زیربخش های ریاضی زیادی عبور می کند. تا آنجا که یک منطقه را می توان با انواع مشکلاتی که به آن پرداخته توصیف کرد، ترکیبات با موارد زیر درگیر است:
- شمارش سازههای مشخص، که گاهی بهعنوان آرایشها یا پیکربندیها به معنایی بسیار کلی، مرتبط با سیستمهای محدود شناخته میشوند،
- وجود چنین ساختارهایی که معیارهای معینی را برآورده می کنند،
- ساخت این سازه ها، شاید از بسیاری جهات، و
- بهینهسازی : یافتن «بهترین» ساختار یا راهحل از میان چندین احتمال، خواه «بزرگترین»، «کوچکترین» یا ارضای برخی معیارهای بهینهسازی دیگر .
لئون میرسکی گفته است: "ترکیبشناسی مجموعهای از مطالعات مرتبط است که وجه اشتراک دارند و در عین حال به طور گسترده در اهداف، روشها و درجه انسجامی که به دست آوردهاند، متفاوت هستند." یکی از راههای تعریف ترکیبها، شاید توصیف زیربخشهای آن با مسائل و تکنیکهایشان باشد. این رویکردی است که در زیر استفاده می شود. با این حال، دلایل صرفاً تاریخی نیز برای گنجاندن یا عدم گنجاندن برخی موضوعات زیر چتر ترکیبیات وجود دارد. اگرچه عمدتاً به سیستم های محدود مربوط می شود، برخی از سؤالات و تکنیک های ترکیبی را می توان به یک تنظیم نامتناهی (به طور خاص، قابل شمارش ) اما گسسته گسترش داد.
ترکیبیات به دلیل گستردگی مشکلاتی که با آن برخورد می کند به خوبی شناخته شده است. مشکلات ترکیبی در بسیاری از حوزههای ریاضیات محض ، به ویژه در جبر ، نظریه احتمال ، توپولوژی ، و هندسه ، و همچنین در بسیاری از حوزههای کاربردی آن به وجود میآیند. بسیاری از سؤالات ترکیبی در طول تاریخ به صورت مجزا در نظر گرفته شده اند، و یک راه حل موقت برای یک مسئله ایجاد شده در برخی زمینه های ریاضی ارائه می دهند. با این حال، در اواخر قرن بیستم، روشهای نظری قدرتمند و کلی توسعه یافتند و ترکیبها را به شاخهای مستقل از ریاضیات تبدیل کردند. یکی از قدیمیترین و در دسترسترین بخشهای ترکیبیات، نظریه گراف است که به خودی خود پیوندهای طبیعی متعددی با سایر حوزهها دارد. ترکیبیات به طور مکرر در علوم کامپیوتر برای به دست آوردن فرمول ها و تخمین ها در تجزیه و تحلیل الگوریتم ها استفاده می شود .
به ریاضیدانی که ترکیبشناسی را مطالعه میکند، ترکیبگرا میگویند .
شاخه های ترکیبیات
[ویرایش]ترکیبات شمارشی
[ویرایش]ترکیبات شمارشی کلاسیکترین دامنه ترکیبات است و بر شمارش تعداد اشیاء ترکیبی خاص تمرکز دارد. اگرچه شمارش تعداد عناصر در یک مجموعه یک مسئله ریاضی نسبتاً گسترده است، بسیاری از مشکلاتی که در کاربردها ایجاد میشوند، توصیف ترکیبی نسبتاً سادهای دارند. اعداد فیبوناچی مثال اصلی یک مسئله در شمارش ترکیب ها هستند. دوازده راه یک چارچوب یکپارچه برای شمارش جایگشت ها، ترکیب ها و پارتیشن ها فراهم می کند.
ترکیبات تحلیلی
[ویرایش]ترکیبات تحلیلی با شمارش ساختارهای ترکیبی با استفاده از ابزارهای تحلیل پیچیده و نظریه احتمال سروکار دارند. برخلاف ترکیبهای شمارشی که از فرمولهای ترکیبی صریح و توابع تولیدکننده برای توصیف نتایج استفاده میکنند، هدف ترکیبهای تحلیلی دستیابی به فرمولهای مجانبی است.
تئوری تقسیم
[ویرایش]نظریه پارتیشن مسائل مختلف شمارش و مجانبی مربوط به پارتیشنهای عدد صحیح را مطالعه میکند و ارتباط نزدیکی با سریهای q، توابع ویژه و چندجملهای متعامد دارد. در ابتدا بخشی از تئوری و تحلیل اعداد بود، اما اکنون بخشی از ترکیب یا یک رشته مستقل در نظر گرفته می شود. این شامل رویکرد دوگانه و ابزارهای مختلف در تحلیل و تئوری تحلیلی اعداد است و مربوط به مکانیک آماری است.
نظریه گراف
[ویرایش]نمودارها اشیاء اساسی در ترکیب بندی ها هستند. ملاحظات تئوری گراف از تعداد (به عنوان مثال، تعداد نمودارها در n رأس با k یال) تا ساختارهای موجود (مانند چرخههای همیلتونی) تا نمایشهای جبری (مثلاً با توجه به نمودار G و دو عدد x و y، توته چندین Do انجام میدهد) را شامل میشود. جملات T G (x، y) تفسیر مختلط دارند؟). اگرچه ارتباط بسیار قوی بین نظریه گراف و ترکیبیات وجود دارد، اما گاهی اوقات به عنوان موضوعات جداگانه در نظر گرفته می شوند.در حالی که روشهای ترکیبی برای بسیاری از مسائل نظریه گراف به کار میروند، این دو رشته عموماً برای یافتن راهحلهایی برای انواع مختلف مسائل استفاده میشوند.
تئوری طراحی
[ویرایش]تئوری طراحی مطالعه طرح های ترکیبی است که مجموعه ای از زیر مجموعه ها با ویژگی های تقاطع متمایز هستند. طرح های بلوک طرح های ترکیبی از نوع خاصی هستند. این ناحیه یکی از قدیمی ترین بخش های ترکیبیات است، مانند مسئله دانشجویی کرکمن که در سال 1850 ارائه شد. راه حل مسئله، مورد خاصی از سیستم اشتاینر است که سیستم ها نقش مهمی در طبقه بندی گروه های ساده محدود دارند. این حوزه بیشتر به نظریه کدگذاری و ترکیبات هندسی مربوط می شود.
هندسه محدود
[ویرایش]هندسه محدود مطالعه سیستم های هندسی است که فقط تعداد محدودی نقطه دارند. ساختارهایی شبیه به آنهایی که در هندسه های پیوسته یافت می شوند (صفحه اقلیدسی، فضای تصویر واقعی و غیره) اما به صورت ترکیبی تعریف شده اند، اصلی ترین ساختارهای مورد مطالعه هستند. این منطقه منبع غنی از نمونه ها برای تئوری طراحی است. نباید آن را با هندسه گسسته (هندسه مرکب) اشتباه گرفت.
تئوری نظم
[ویرایش]نظریه نظم مطالعه مجموعه های جزئی منظم، متناهی و نامتناهی است. نمونه های مختلفی از نظم جزئی در جبر، هندسه، نظریه اعداد، و در سراسر ترکیبات و نظریه گراف ظاهر می شود. کلاس ها و نمونه های قابل توجهی از نظم های جزئی شامل شبکه ها و جبرهای بولی است.
نظریه ماتروئید
[ویرایش]نظریه ماتروئید بخشی از هندسه را انتزاعی می کند. ویژگی مجموعه ها (معمولا مجموعه های محدود) بردارهایی را در فضای برداری مطالعه می کند که به ضرایب خاصی در یک رابطه وابستگی خطی وابسته نیستند. نه تنها ساختار، بلکه خواص شمارش نیز متعلق به نظریه ماتروئید است. نظریه ماتروئید توسط هاسلر ویتنی معرفی شد و به عنوان بخشی از نظریه نظم مورد مطالعه قرار گرفت. اکنون یک رشته تحصیلی مستقل با تعدادی از ارتباطات با سایر بخش های ترکیبی است.
ترکیبات افراطی
[ویرایش]ترکیبات اکسترمال به بررسی سوالات اکسترمال در سیستم های مجموعه می پردازد. انواع سوالات مطرح شده در این مورد در مورد بزرگترین نمودار ممکن است که ویژگی های خاصی را برآورده می کند. به عنوان مثال، بزرگترین نمودار بدون مثلث در 2n راس، یک گراف دو قسمتی کامل Kn، n است. حتی یافتن پاسخ افراطی دقیق f(n) اغلب بسیار دشوار است و فقط می توان یک تخمین مجانبی ارائه داد. نظریه رمزی بخش دیگری از ترکیبات افراطی است. بیان می کند که هر پیکربندی به اندازه کافی بزرگ حاوی یک نظم است. این یک تعمیم پیشرفته از اصل کبوتر است.
ترکیبات احتمالی
[ویرایش]در ترکیبات احتمالی، سؤالات این است: احتمال یک ویژگی خاص برای یک شی گسسته تصادفی، مانند یک نمودار تصادفی چقدر است؟ به عنوان مثال، میانگین تعداد مثلث ها در یک نمودار تصادفی چقدر است؟ روشهای احتمالی نیز برای تعیین وجود اشیاء مرکب با ویژگیهای تجویز شده خاص (که یافتن مثالهای صریح ممکن است دشوار باشد) استفاده میشود، صرفاً با مشاهده اینکه احتمال انتخاب تصادفی یک شی با آن ویژگیها بیشتر از 0 است. اغلب به آن اشاره میشود. به عنوان روش احتمالی) در کاربرد ترکیبات اکسترمال و نظریه گراف بسیار مؤثر بود. یک منطقه نزدیک مطالعه زنجیره های مارکوف محدود، به ویژه در اجسام مرکب است. در اینجا دوباره از ابزارهای احتمالی برای تخمین زمان اختلاط استفاده می شود.
ترکیبات جبری
[ویرایش]ترکیبهای جبری رشتهای از ریاضیات است که از روشهای جبر انتزاعی بهویژه نظریه گروهی و نظریه نمایش در زمینههای ترکیبی مختلف استفاده میکند و بالعکس از تکنیکهای ترکیببندی برای مسائل جبر استفاده میکند. ترکیبات جبری به طور مداوم در حال گسترش دامنه خود است، هم در موضوعات و هم در تکنیک ها، و می تواند به عنوان حوزه ای از ریاضیات در نظر گرفته شود که در آن تعامل روش های ترکیبی و جبری به ویژه قوی و قابل توجه است.
ترکیبات هندسی
[ویرایش]ترکیبات هندسی مربوط به هندسه محدب و گسسته، به ویژه ترکیبات چند وجهی است. به عنوان مثال، می پرسد که یک پلی توپ محدب چند وجه از هر بعد می تواند داشته باشد. خواص متریک پلی توپ ها نیز نقش مهمی ایفا می کند، برای مثال قضیه کوشی در مورد صلبیت پلی توپ های محدب. پلی توپ های ویژه نیز در نظر گرفته می شوند، مانند پلی توپ های پرموتوهدرا، اسوکیاهدرا و بیرخوف. هندسه ترکیبی نامی تاریخی برای هندسه گسسته است.
ترکیبات حسابی
[ویرایش]ترکیبهای حسابی از تعامل بین نظریه اعداد، ترکیبها، نظریه ارگودیک و تحلیل هارمونیک پدید آمدند. این در مورد تخمین های مرکب مربوط به عملیات حسابی (جمع، تفریق، ضرب و تقسیم) است. نظریه اعداد جمعی (گاهی اوقات ترکیبات جمعی نامیده می شود) به یک مورد خاص اشاره دارد که در آن فقط عملیات جمع و تفریق درگیر است. یکی از تکنیک های مهم در ترکیب های حسابی، نظریه ارگودیک سیستم های دینامیکی است
ترکیبات بی نهایت
[ویرایش]ترکیبات نامتناهی یا ترکیبات بی نهاییت یا تئوری مجموعه های ترکیبی امتدادی از ایده های ترکیبیات به مجموعه های نامتناهی است. این بخشی از تئوری مجموعه ها، حوزه ای از منطق ریاضی است، اما از ابزارها و ایده هایی از نظریه مجموعه ها و ترکیبات افراطی استفاده می کند. جیان کارلو روتا از نام ترکیب های پیوسته برای توصیف احتمال هندسی استفاده کرد، زیرا شباهت های زیادی بین شمارش و اندازه گیری وجود دارد.
منابع
[ویرایش]ویکی پدیای انگلیسی
نظریه گراف
در ریاضیات ، نظریه گراف مطالعه نمودارها است ، که ساختارهای ریاضی هستند که برای مدلسازی روابط زوجی بین اشیاء استفاده میشوند. یک نمودار در این زمینه از رئوس (که گره ها یا نقاط نیز نامیده می شوند ) ساخته شده است که توسط یال ها (که پیوندها یا خطوط نیز نامیده می شوند) به هم متصل می شوند . بین نمودارهای بدون جهت ، که در آن یال ها دو راس را به طور متقارن به هم مرتبط می کنند، و نمودارهای جهت دار ، که در آن یال ها دو راس را به طور نامتقارن به هم مرتبط می کنند، تمایز قائل می شوند. نمودارها یکی از موضوعات اصلی مطالعه در ریاضیات گسسته هستند.
تاریخ
[ویرایش]برخلاف شاخههای دیگر ریاضیات، سیر نظریهٔ گراف آغاز معینی در زمان و مکان دارد و آن مسئلهٔ هفت پل کونیگسبرگ است که در سال ۱۷۳۶ توسط لئونارد اویلر حل شد. در سال ۱۷۵۲ قضیهٔ اویلر برای گرافهای مسطح ارائه میشود. اما پس از آن به مدت تقریباً یک قرن فعالیت اندکی در این زمینه صورت گرفت.
تعریف
[ویرایش]تعریف دقیقتر گراف به این صورت است، که گراف مجموعهای از رأسها است، که توسط خانوادهای از زوجهای مرتب که همان یالها هستند به هم مربوط (وصل) شدهاند.
یالها بر دو نوع ساده و جهت دار هستند، که هر کدام در جای خود کاربردهای بسیاری دارد؛ مثلاً اگر صرفاً اتصال دو نقطه -مانند اتصال تهران و زنجان با کمک آزادراه- مد نظر شما باشد، کافیست آن دو شهر را با دو نقطه نمایش داده، و اتوبان مزبور را با یالی ساده نمایش دهید. اما اگر بین دو شهر جادهای یکطرفه وجود داشته باشد آنگاه لازمست تا شما با قرار دادن یالی جهت دار مسیر حرکت را در آن جاده مشخص کنید. همچنین برای اینکه فاصله بین دو شهر را در گراف نشان دهید، میتوانید از گراف وزن دار استفاده کنید و مسافت بین شهرها را با یک عدد بر روی هر یال نشان دهید.
آغاز نظریهٔ گراف به سدهٔ هجدهم بر میگردد. لئونارد اویلر ریاضیدان بزرگ مفهوم گراف را برای حل مسئله پلهای کونیگسبرگ ابداع کرد اما رشد و پویایی این نظریه عمدتاً مربوط به نیم سدهٔ اخیر و با رشد علم انفورماتیک بودهاست.
مهمترین کاربرد گراف مدلسازی پدیدههای گوناگون و بررسی بر روی آنهاست. با گراف میتوان به راحتی یک نقشه بسیار بزرگ یا شبکهای عظیم را در درون یک ماتریس به نام ماتریس وقوع گراف ذخیره کرد یا الگوریتمهای مناسب مانند الگوریتم دایکسترا یا الگوریتم کروسکال و… را بر روی آن اعمال نمود.
یکی از قسمتهای پرکاربرد نظریهٔ گراف، گراف مسطح است که به بررسی گرافهایی میپردازد که میتوان آنها را به نحوی روی صفحه کشید که یالها جز در محل رأسها یکدیگر را قطع نکنند. این نوع گراف در ساخت جادهها و حل مسئله کلاسیک و قدیمی سه خانه و سه چاه آب به کار میرود.
نظریه گراف یکی از پرکاربردترین نظریهها در شاخههای مختلف علوم مهندسی (مانند عمران)، باستانشناسی (کشف محدوده یک تمدن) و… است.
روابط میان رأسهای یک گراف را میتوان با کمک ماتریس بیان کرد.
برای نمایش تصویری گرافها معمولاً از نقطه یا دایره برای کشیدن رأسها و از کمان یا خط راست برای کشیدن یال بین رأسها استفاده میشود.
کاربرد
[ویرایش]نمودارها را میتوان برای مدلسازی بسیاری از انواع روابط و فرآیندها در سیستمهای فیزیکی، بیولوژیکی،اجتماعی و اطلاعاتی استفاده کرد.بسیاری از مسائل عملی را می توان با نمودار نشان داد. با تأکید بر کاربرد آنها در سیستم های دنیای واقعی، اصطلاح شبکه گاهی اوقات به معنای نموداری تعریف می شود که در آن ویژگی ها (مثلاً نام ها) با رئوس و یال ها مرتبط هستند و موضوعی که سیستم های دنیای واقعی را به عنوان یک علم شبکه بیان و درک می کند نامیده می شود.
علوم کامپیوتر
[ویرایش]در علم کامپیوتر ، سایبرنتیک از نمودارها برای نمایش شبکه های ارتباطی، سازماندهی داده ها، دستگاه های محاسباتی، جریان محاسبات و غیره استفاده می کند. به عنوان مثال، ساختار پیوند یک وب سایت را می توان با یک نمودار جهت دار نشان داد که در آن رئوس نشان دهنده صفحات وب است. و لبه های جهت دار نشان دهنده پیوندها از یک صفحه به صفحه دیگر است. رویکرد مشابهی را می توان برای مشکلات در رسانه های اجتماعی، سفر، زیست شناسی، طراحی تراشه های کامپیوتری، نقشه برداری از پیشرفت بیماری های عصبی، و بسیاری از زمینه های دیگر اتخاذ کرد. بنابراین توسعه الگوریتمهایی برای مدیریت نمودارها از علاقهمندی عمده در علوم کامپیوتر است. راتبدیل نمودارها اغلب رسمی و با سیستم های بازنویسی نمودار نشان داده می شود . مکمل سیستمهای تبدیل گراف که بر روی دستکاری در حافظه مبتنی بر قانون گرافها تمرکز میکنند، پایگاههای اطلاعاتی گراف هستند که برای ذخیرهسازی پایدار ، ذخیرهسازی پایدار و پرسوجو از دادههای ساختار یافته گراف طراحی شدهاند.
ریاضیات
[ویرایش]در ریاضیات، نمودارها در هندسه و بخش های خاصی از توپولوژی مانند نظریه گره مفید هستند . نظریه گراف جبری پیوند نزدیکی با نظریه گروه دارد . نظریه گراف جبری در بسیاری از زمینه ها از جمله سیستم های پویا و پیچیدگی به کار گرفته شده است.
فیزیک و شیمی
[ویرایش]تئوری گراف همچنین برای مطالعه مولکول ها در شیمی و فیزیک استفاده می شود. در فیزیک ماده چگال ، ساختار سه بعدی ساختارهای اتمی شبیهسازی شده پیچیده را میتوان با جمعآوری آماری در مورد ویژگیهای نظری گراف مرتبط با توپولوژی اتمها به صورت کمی مطالعه کرد. همچنین، « نمودارهای فاینمن و قواعد محاسباتی ، نظریه میدان کوانتومی را به شکلی در ارتباط نزدیک با اعداد تجربی که میخواهیم بفهمیم، خلاصه میکنند». در شیمی، یک نمودار یک مدل طبیعی برای یک مولکول می سازد، که در آن رئوس نشان دهنده اتم ها و پیوندهای لبه است.. این رویکرد به ویژه در پردازش کامپیوتری ساختارهای مولکولی، از ویرایشگرهای شیمیایی تا جستجو در پایگاه داده استفاده می شود. در فیزیک آماری ، نمودارها می توانند ارتباطات محلی بین بخش های متقابل یک سیستم و همچنین پویایی یک فرآیند فیزیکی در چنین سیستم هایی را نشان دهند. به طور مشابه، در علوم اعصاب محاسباتیاز نمودارها می توان برای نشان دادن ارتباطات عملکردی بین نواحی مغز استفاده کرد که با یکدیگر تعامل دارند و فرآیندهای شناختی مختلفی را ایجاد می کنند، جایی که رئوس نشان دهنده مناطق مختلف مغز و لبه ها نشان دهنده ارتباطات بین آن مناطق هستند. تئوری نمودار نقش مهمی در مدلسازی الکتریکی شبکههای الکتریکی ایفا میکند، در اینجا وزنها با مقاومت قطعات سیم برای به دست آوردن خواص الکتریکی سازههای شبکه مرتبط میشوند. نمودارها همچنین برای نشان دادن کانالهای میکرو مقیاس محیط متخلخل استفاده میشوند که در آن رئوس نشاندهنده منافذ و لبهها کانالهای کوچکتر را نشان میدهند که منافذ را به هم متصل میکنند. نظریه گراف شیمیایی از گراف مولکولی استفاده می کندبه عنوان وسیله ای برای مدل سازی مولکول ها. نمودارها و شبکه ها مدل های عالی برای مطالعه و درک انتقال فاز و پدیده های بحرانی هستند. حذف گره ها یا لبه ها منجر به یک انتقال بحرانی می شود که در آن شبکه به خوشه های کوچک تقسیم می شود که به عنوان یک انتقال فاز مورد مطالعه قرار می گیرد. این تفکیک از طریق تئوری نفوذ بررسی می شود .
منابع
[ویرایش]
هندسه دیجیتال
هندسه دیجیتال با مجموعههای گسسته (به طور کلی مجموعهای از نقاط گسسته) سر و کار دارد که مدلهای دیجیتال یا تصاویر اشیاء دو بعدی و سه بعدی در فضای اقلیدسی در نظر گرفته میشوند. برای جایگزینی یک شی با مجموعهای گسسته از نقاط آن، با اعداد نشان داده میشود. تصاویری که روی صفحه تلویزیون یا روزنامهها میبینیم در واقع تصاویر دیجیتالی هستند. کاربردهای اصلی هندسه دیجیتال در زمینه گرافیک کامپیوتری و تحلیل تصویر است.
زمینههای اصلی
[ویرایش]- ایجاد نمایش رقمی اشیا با تأکید بر دقت و کارایی (با استفاده از ترکیب مثلاً الگوریتم خط برسنهام یا دیسکهای دیجیتال یا به صورت رقم درآوردن و پردازش متوالی تصاویر دیجیتال).
- مطالعهٔ خواص مجموعههای دیجیتال برای مثال قضیه پیک، تحدب دیجیتال، صافی دیجیتال و مسطح بودن دیجیتال
- تغییر نمایش رقمی اشیا به (آ) اشیا ی ساده شده همچون اسکلتها (از طریق پاک کردن مکرر نقاط ساده طوریکه توپولوژی دیجیتال تصویر تغییر نکند)، (ب) اشکال تغییر یافته با استفاده از شکلشناسی ریاضیاتی
- بازسازی اشیای واقعی یا خواص آنها (ناحیه، طول، حجم، سطح و…) از روی تصاویر دیجیتال.
هندسه دیجیتال ارتباط زیادی با هندسه گسسته دارد و میتوان آن را بخشی از هندسه گسسته در نظر گرفت.
فضای دیجیتال
[ویرایش]فضای دیجیتال دو بعدی معمولاً به معنای یک فضای شبکه دو بعدی است که فقط شامل نقاط صحیح در فضای اقلیدسی دوبعدی است. تصویر دوبعدی تابعی در فضای دیجیتال دو بعدی است (به پردازش تصویر مراجعه کنید). در کتاب روزنفلد و کاک، اتصال دیجیتال به عنوان رابطه بین عناصر در فضای دیجیتال تعریف شده است. به عنوان مثال، ۴-اتصال و ۸-اتصال در 2D. همچنین اتصال پیکسل را ببینید. یک فضای دیجیتال و اتصال (دیجیتال) آن یک توپولوژی دیجیتال را تعیین میکند. در فضای دیجیتال، تابع پیوسته دیجیتالی (A. Rosenfeld، ۱۹۸۶) و تابع تدریجی متغیر (L. Chen, 1989) به طور مستقل پیشنهاد شدند. تابع پیوسته دیجیتالی به معنای تابعی است که در آن مقدار (یک عدد صحیح) در یک نقطه دیجیتال یکسان یا حداکثر ۱ از همسایگانش خاموش باشد. به عبارت دیگر، اگر «x» و «y» دو نقطه مجاور در یک فضای دیجیتالی باشند، |f(x) &منهای؛ f(y)| ≤ ۱. تابع تغییر تدریجی تابعی است از فضای دیجیتال تا که در آن اعداد واقعی هستند. این تابع دارای ویژگی زیر است: اگر "x" و "y" دو نقطه مجاور در هستند، را فرض کنید، سپس ، ، یا . بنابراین میتوانیم ببینیم که تابع تغییر تدریجی به طور کلی تر از تابع پیوسته دیجیتالی تعریف شده است. یک قضیه بسط مربوط به توابع بالا ذکر شد و توسط (L. Chen 1989) تکمیل شد. این قضیه بیان میکند: فرض کنید و . شرط لازم و کافی برای وجود پسوند تدریجی متغیر از این است: برای هر جفت نقطه و در ، فرض کنید و ، ما داریم ، فاصله (دیجیتال) بین واست.
منابع
[ویرایش]ویکیپدیای فارسی
ویکیپدیای انگلیسی
توپولوژی دیجیتال
توپولوژی دیجیتال به خواص و شکل تصاویر دیجیتالی دو بعدی یا سه بعدی اشیاء در رابطه با خواص توپولوژیکی (اتصال) یا شکل توپولوژیکی (مرزها) میپردازد. مفاهیم و نتایج توپولوژی برای تعریف و تأکید بر الگوریتمهای مهم تجزیه و تحلیل تصویر استفاده میشود. توپولوژی دیجیتال اولین بار در اواخر دهه ۱۹۶۰ توسط محقق تجزیه و تحلیل تصویر کامپیوتری ازریل روزنفلد (۱۹۳۱-۲۰۰۴) مورد مطالعه قرار گرفت. انتشارات او در این زمینه نقش اساسی در ایجاد و گسترش این حوزه داشت. اصطلاح توپولوژی دیجیتال نیز ابتکار خود روزنفلد بود که برای اولین بار در سال ۱۹۷۳ در یکی از انتشارات خود از آن استفاده کرد. یک نتیجه مهم در توپولوژی دیجیتال بیان میکند که تصاویر باینری دو بعدی به انتخاب اختیاری ۴ مجاورت یا ۸ مجاورت نیاز دارند تا از دوگانگی توپولوژیکی اولیه الحاق و جداسازی اطمینان حاصل شود. تصاویر دیجیتال آرایههای مستطیلی از اعداد غیر منفی هستند. برای تجزیه و تحلیل یک عکس دیجیتال معمولاً آن را به قسمتهای مختلف و ویژگیهای مختلف تقسیم میکنند و رابطه بین قسمتها بررسی و مقایسه میشود. پردازش تصویر دیجیتال یا پردازش تصویر کاربرد گستردهای در زمینههای مختلف از جمله تجارت، صنعت، پزشکی و علوم محیطی دارد.
نتایج اساسی
[ویرایش]یک نتیجه اولیه (اولیه) در توپولوژی دیجیتال میگوید که تصاویر دوبعدی دوبعدی به استفاده جایگزین از مجاورت ۴ یا ۸ یا «اتصال پیکسل» (برای «شی» یا «غیر شی» نیاز دارند. پیکسل) برای اطمینان از دوگانگی توپولوژیکی اصلی جداسازی و اتصال. این استفاده جایگزین مربوط به باز یا بسته است در ۲ بعدی توپولوژی سلول شبکهای تنظیم میشود و نتیجه به ۳ بعدی تعمیم مییابد: استفاده جایگزین ۶ یا ۲۶ مجاورت مطابقت دارد برای باز یا بسته کردن مجموعهها در سه بعدی توپولوژی سلول شبکه. توپولوژی سلول شبکه همچنین برای تصاویر دو بعدی یا سه بعدی چند سطحی (به عنوان مثال، رنگی) اعمال میشود. به عنوان مثال بر اساس یک ترتیب کلی از مقادیر تصویر ممکن و به کار بردن یک قانون حداکثر برچسب (به کتاب Klette و Rosenfeld، ۲۰۰۴ مراجعه کنید). توپولوژی دیجیتال بسیار با توپولوژی ترکیبی مرتبط است. تفاوتهای اصلی بین آنها عبارتند از:
- توپولوژی دیجیتال عمدتاً اشیاء دیجیتالی را که توسط سلولهای شبکه تشکیل میشوند مطالعه میکند
- توپولوژی دیجیتال نیز با منیفولدهای غیر اردن «منیفولد ترکیبی» نوعی منیفولد است که گسسته سازی یک منیفولد است. این معمولاً به معنای منیفولد خطی تکهای ساخته شده توسط کمپلکسهای ساده است. یک منیفولد دیجیتال نوع خاصی از منیفولد ترکیبی است که در فضای دیجیتال یعنی فضای سلول شبکهای تعریف میشود. یک شکل دیجیتالی قضیه گاوس-بونت این است: فرض کنید «M» یک ۲ بعدی دیجیتال بسته منیفولد در مجاورت مستقیم باشد (یعنی سطح (۶٬۲۶) در سه بعدی). فرمول جنس است: ،
که در آن مجموعهای از نقاط سطحی را نشان میدهد که هر کدام دارای نقاط مجاور "i" در سطح هستند (چن و رونگ، ICPR 2008). اگر M به سادگی متصل باشد، یعنی ، سپس . (ویژگی اویلر را نیز ببینید)
همبندی
[ویرایش]ابتدا مفهوم همبند بودن را برای زیرمجموعههای تصویر Img به صورت فرمول بیان میکنیم. فرض میکنیم Img یک ارائه از نقاط شبکه بندی با مختصات صحیح (x,y) باشد که x و y اعدادی طبیعی در یک بازه بسته هستند.
تعریف۱: ۴-همسایههای (x,y) چهار نقطهٔ مجاور عمودی و افقی به آن یعنی (x±۱,y) و (x, y±۱) هستند.
تعریف ۲: ۸-همسایههای (x,y) شامل ۴-همسایهها و نقاط مجاور قطری آن (x+1, y±۱) و (x-1, y±۱) هستند.
اگر نقاط P و Q از Img همسایه باشند به آنها ۴-مجاور یا ۸-مجاور میگوییم.
تعریف۳: P و Q نقاطی در Img هستند، منظور از مسیر از P تا Q دنبالهای از نقاط مانند P=,,…,=Q است بهطوریکه همسایهٔ باشد.
فرض کنیم S یک زیرمجموعه از Img باشد. برای دوری از حالات خاص فرض میکنیم S شامل مرز Img نیست.
تعریف۴: میگوییم P و Q در Sمتصل (همبند) هستند اگر یک مسیر از P به Q وجود داشته باشد بهطوریکه همهٔ نقاط مسیر نقاطی از S باشند.
گزاره: همبندی یک رابظهٔ همارزی است.
تعریف۵: دستههای همارزی تعریف شده با این رابطه سازههای S نامیده میشوند. اگر S فقط یک سازه داشته باشد همبند نامیده میشود. اگر Sc متمم S باشد، سازهٔ یکتایی از Sc که شامل مرز Img است، پیش زمینه S نامیده میشود. هر سازهٔ دیگری که وجود داشته باشد سوراخ نامیده میشود. اگر S هیچ سوراخی نداشته باشد تماماً همبند نامیده میشود.
دنبال کردن مرز مشخصه دنباله
[ویرایش]S زیر مجموعهای از Img است مرزِ S مجموعهای از نقاط S است که در مکمل آن ۴-همسایه دارند.
تعریف: اگر C یک سازهٔ S و D یک سازهٔ Sc باشد. D-مرزِ C مجموعهای از نقاط C است که در دی ۴-همسایه دارند. این مرز را با نشان میدهیم.
اکنون الگوریتمی را توضیح میدهیم که متوالیاً از همهٔ نقاط D-مرزِ C عبور میکند. این الگوریتم که نام دارد نشان میدهد که چگونه با داشتن یک جفت نقطه (,) جفت نقطهٔ جدید (,) پیدا میشوند. ۸-همسایههای را در خلاف جهت عقربههای ساعت که با شروع میشوند را =, ,…, مینامیم. فرض کنیم اولین R ای باشد که در C است و یک ۴-همسایهٔ باشد. چنین ای باید وجود داشته باشد چون سی ۴-همبند است و بیشتر از یک نقطه دارد. اگر در D باشد، را میگیریم و را ، در غیر این صورت را و را میگیریم. اگر برای یک i مثبت برابر شد و یکی از ,…, برابر ، کار تمام است.
منابع
[ویرایش]ویکیپدیای فارسی
ویکیپدیای انگلیسی
نظریهٔ محاسبهپذیری
محاسبهپذیری توانایی حل یک مسئله به روشی مؤثر است؛ که یک موضوع کلیدی در زمینه نظریه محاسبه پذیری در منطق ریاضی و نظریه محاسبات در علوم کامپیوتر است. محاسبهپذیری یک مسئله ارتباط نزدیکی با وجود یک الگوریتم برای حل مسئله دارد. گستردهترین مدلهای مورد مطالعه از محاسبات توابع تورینگ-محاسبه پذیر، μ-بازگشتی و حساب لامبدا هستند، که تمامی آنها دارای قدرت محاسباتی معادل هستند. از انواع دیگر مطالعه محاسبه پذیری، همچنین: مفاهیم محاسبهپذیری ضعیف تر از ماشینهای تورینگ که در نظریه اتوماتا مطالعه میشود و مفاهیم محاسبهپذیری قوی تر از ماشین تورینگ که در زمینه hypercomputation مطالعه میشود را میتوان نام برد.
مسائل
[ویرایش]ایده اساسی در محاسبهپذیری این است که یک مسئله که یک task است که محاسبهپذیری ان را میتوان بررسی کرد. دو نوع اصلی از مسایل وجود دارد:
مسئلهٔ تصمیم پذیری، یک مجموعه S را معین میکند که ممکن است مجموعهای از رشتهها، اعداد طبیعی، یا اشیاء دیگری باشد که از مجموعه بزرگتری مانند U امدهاند باشد. یک مثال خاص از مسئله تصمیمگیری این است که ایا یک عنصر u دلخواه از U در S است. به عنوان مثال، اکر U مجموعهٔ اعداد طبیعی و S مجموعهٔ اعداد اول باشد، مسئلهٔ تصمیمگیری به تصمیمگیری اول بودن تبدیل میشود.
مسئلهٔ تابع، شامل یک تابع f از مجموعه U به V است. مجموعه به عنوان یک نمونه از مسئله محاسبهٔ مقدار تابع f برای u داده شده از مجموعه U است. به عنوان مثال، اگر U و V مجموعهٔ تمام رشتههای دودویی متناهی باشند و f یک رشته را گرفته و معکوس آن را به عنوان خروجی برگرداند آنگاه f(۱۰۱۰) = ۱۰۱۰.
انواع دیگر مسایل شامل مسایل جستجو و مسایل بهینهسازی هستند.
یکی از اهداف نظریه محاسبهپذیری تعیین این است که کدام مسایل، یا کلاسی از مسئلهها، قابل حل در کدام یک از مدلهای محاسبهپذیری هستند.
مدل های مبتنی بر هنزمانی
[ویرایش]تعدادی از مدلهای محاسباتی مبتنی بر همزمانی توسعه یافتهاند، از جمله ماشین دسترسی تصادفی موازی و شبکه پتری . این مدلهای محاسبات همزمان هنوز هیچ توابع ریاضی را که توسط ماشینهای تورینگ قابل پیادهسازی نباشد، اجرا نمیکنند.
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
تقسیم طولانی چندجمله ای
تقسیم طولانی چندجملهای،شاخهای از جبر و نوعی الگوریتم بهحساب میآید که در مورد تقسیمهای اتحادی یا چندجملهای میپردازد که شامل چندجمله ای هایی مثل تکجمله٬دوجملهای٬سهجملهای و... است.تقسیم چندجملهای نوعی تقسیم اقلیدسی است و به آن تقسیممصنوعی نیز میگوید.این تقسیم را اولین بار اقلیدوس استفاده کرد و بهاسم او نامگذاری شدهاست.
تقسیم چندجملهای به سه دسته تقسیم میشوند
- تقسیم تکجملهای بر تکجملهای
- تقسیم تکجملهای بر چندجملهای
- تقسیم چندجملهای بر چندجملهای
تعاریف
[ویرایش]تعریف تقسیم و اجزای آن
[ویرایش]در تقسیم سه اصل وجود دارد که در تمامی تقسیم ها وجود دارد
۱-مقسوم
۲-مقسومعلیه
۳-خارجقسمت
مقسوم:به آنچیزی که مورد تقسیم قرار میگیرد گویند.
مقسوم علیه:به آن چیزی که عامل تقسیم کردن مقسوم است گویند.
خارجقسمت:به آن چیزی که مقسوم تا حد امکان دارد که از حاصلضرب با مقسوم علیه و با اضافه با باقیمانده مقسوم را به وجود میآورد گویند.
نکته:درتقسیم ها هر گاه باقی مانده صفر شود می گوییم مقسوم بر مقسوم علیه بخش پذیر است.
تعریف تقسیم های چندجمله ای
[ویرایش]تقسیم تک جمله ای بر تک جمله ای:به تقسیمی گفته میشود که یک تک جمله بر یک تک جمله دیگری تقسیم میشود. این تقسیم فقط یک تقسیم ضربی جبری در اتحاد های تکی است:(4ab=4×(ab
در این تقسیم
مقسوم علیه:کوچکترین عبارت تک جمله ای
خارج قسمت:مقدار متوسط عبارت تک جمله ای
مقسوم:بزرگترین عبارت تک جمله ای
مثال:
تقسیم چندجمله ای بر چند جمله ای:به تقسیمی گفته می شود که یک چندجمله ای بر یک تک جمله ای تقسیم می شود مقسوم علیه عبارت تک جمله ای است و مقسوم چند جمله ای است.چند جمله ای دارای عبارت های تک جمله ای دارای جمع شدن است می گویند.
دراین تقسیم مقسومعلیه:کوچکترین عبارت تک جمله ای است مقسوم: بزرگترین چند جمله ای جمله ای خارج قسمت:یک عبارت چند جمله ای است و مقدار مقدار میانی دارد.
مثال:
تقسیم چندجمله ای بر چند جمله ای:به تقسیمی گفته میشود مقسوم و مقسوم علیه و خارج قسمت آن چند جمله ای باشد و باقی مانده ممکن است چند جمله ای یا تک جمله ای یا صفر باشد؛در این تقسیم خارج قسمت باید بر اساس توان های نزولی که در مقسوم علیه ضرب و از باقی مانده جمع میشود برقرار باشد. در این تقسیم
مقسوم علیه:کوچکترین مقدار چند جمله ای
خارج قسمت:مقدار متوسط چند جمله ای
مقسوم:بزرگترین مقدار چند جمله ای
مثال تقسیم:
رابطه نویسی
[ویرایش]تقسیم طولانی چند جملهای الگوریتمی است که تقسیم اقلیدسی چندجملهای را پیادهسازی میکند ، که با شروع از دو چندجملهای A (بخش تقسیمکننده ) و B ( مقسومکننده ) اگر B صفر نباشد، یک ضریب Q و یک باقیمانده R تولید میکند.
A = BQ + R
مثال:
مقسوم:
مقسومعلیه:
خارجقسمت:
باقیمانده:
رابطه اینگونه نوشته میگردد:
تقسیم چندجمله ای مشتقی
[ویرایش]تقسیم چندجمله ای مشتقی به تقسیمی گفته می شود که اتحاد چندجمله ای به صورت چندجمله ای مشتقی باشد که به ترتیب توان های آن در ضریب چندجمله ای ضرب شده و توان از آن به ازای یکی یکی کم می شود.
مثال
[ویرایش]حاصل ضرب دو اتحاد چندجمله ای مشتقی برابر بااست که مقسوم علیه آن برابر بااست.خارج قسمت و باقی مانده را بیابید.
حل
[ویرایش]طبق این کار تقسیم را انجام می دهیم
بعد با انجام عملیات تقسیم به این رابطه می رسیم
- خارج قسمت:
- باقی مانده:
برنامه های کاربردی
[ویرایش]فاکتورگیری چند جمله ای ها
[ویرایش]گاهی اوقات یک یا چند ریشه از یک چند جمله ای شناخته می شود که شاید با استفاده از قضیه ریشه گویا پیدا شده باشد. اگر یک ریشه r از یک چند جمله ای P ( x ) درجه n شناخته شده باشد، می توان از تقسیم طولانی چند جمله ای برای فاکتور P ( x ) به شکل ( x − r ) ( Q ( x )) استفاده کرد که در آن Q ( x ) a است. چند جمله ای درجه n - 1. Q ( x ) به سادگی ضریب به دست آمده از فرآیند تقسیم است. از آنجایی که rبه عنوان ریشه P ( x ) شناخته می شود، معلوم است که باقیمانده باید صفر باشد.
به همین ترتیب، اگر بیش از یک ریشه شناخته شده باشد، یک عامل خطی ( x - r ) در یکی از آنها ( r ) را می توان برای بدست آوردن Q ( x ) تقسیم کرد و سپس یک جمله خطی در ریشه دیگر، s ، را می توان تقسیم کرد. از Q ( x ) و غیره. متناوباً، همه آنها را می توان یکباره تقسیم کرد: برای مثال عوامل خطی x - r و x - s را می توان با هم ضرب کرد تا ضریب درجه دوم x۲ - ( r + s ) x به دست آید. + rs،که سپس می توان آن را به چند جمله ای اصلی (P (x تقسیم کرد تا یک ضریب درجه n - 2 به دست آورد.
به این ترتیب، گاهی اوقات می توان تمام ریشه های یک چند جمله ای با درجه بزرگتر از چهار را به دست آورد، هرچند که همیشه ممکن نیست. به عنوان مثال، اگر قضیه ریشه گویا را بتوان برای به دست آوردن یک ریشه منفرد (گویا) از یک چند جملهای پنججملهای استفاده کرد، میتوان آن را برای به دست آوردن یک ضریب کوارتیک (درجه چهارم) فاکتور گرفت. فرمول صریح ریشههای یک چند جملهای چهار جملهای را میتوان برای یافتن چهار ریشه دیگر کوانتیک استفاده کرد.
یافتن مماس بر توابع چندجمله ای
[ویرایش]تقسیم طولانی چند جمله ای را می توان برای یافتن معادله خط مماس بر نمودار تابع تعریف شده توسط چند جمله ای (P (x در یک نقطه خاص x = r استفاده کرد. اگر (R (x باقیمانده تقسیم (P (x بر x – r ) 2) باشد ، آنگاه معادله خط مماس در x = r به نمودار تابع (y = P (x است.
(y =R(x است، صرف نظر از اینکه r ریشه چند جمله ای باشد یا نه.
مثال
[ویرایش]معادله خطی را که بر منحنی زیر مماس است در x = 1 بیابید :
با تقسیم چند جمله ای بر ( x − 1 2 = x 2 − 2 x + 1) شروع کنید :
خط مماس y = −21 x − 32 است.
بررسی افزونگی چرخه ای
[ویرایش]بررسی افزونگی چرخهای از باقیمانده تقسیم چند جملهای برای شناسایی خطاها در پیامهای ارسالی میکند.
منابع
[ویرایش]ویکی پدیای انگلیسی
ریاضی پایه نهم دوره متوسطه اول(درس سوم فصل۷)
حساب دیفرانسیل
در ریاضیات، حساب دیفرانسیل یکی از زیرمجموعههای حسابان است که به مطالعهٔ نرخ تغییرات کمیتها میپردازد. این حساب یکی از دو بخش سنتی حسابان است که بخش دیگر آن، حساب انتگرال است.
هدف اصلی مطالعهٔ حساب دیفرانسیل، محاسبهٔ تغیرات یک تابع و کاربردهای آن است. مشتق تابع در یک نقطهٔ دلخواه، نرخ تغییرات تابع در آن نقطه را توصیف میکند. فرایند یافتن مشتق، مشتقگیری نامیده میشود. از نظر هندسی، مشتق در یک نقطه شیب خط مماس روی نمودار تابع با جهت مثبت محور طولها در همان نقطه است؛ به شرطی که مشتق در آن نقطه موجود باشد. مشتق تابع حقیقی یکمتغیره در هر نقطه، بهترین تقریب خطی برای تابع در آن نقطه است.
حساب دیفرانسیل و حساب انتگرال با قضیهٔ اساسی حسابان به یکدیگر مرتبط میشوند. این قضیه بیان میکند که مشتقگیری معکوس انتگرالگیری است.
مشتقگیری تقریباً در همهٔ علوم کمّی کاربرد دارد. برای نمونه، در فیزیک، مشتق جابجایی یک جسم متحرک برحسب زمان نشان دهندهٔ سرعت آن جسم و مشتق سرعت برحسب زمان بیانگر شتاب است. مشتق تکانهٔ یک جسم معادل با نیروی وارد بر آن جسم است و بازنویسی این مشتقگیری معادلهٔ معروف F=ma را که متناظر با قانون دوم حرکت نیوتن است، به دست میدهد. نرخ واکنش یک واکنش شیمیایی، یک مشتق است. مشتقات در تحقیق در عملیات، پربازدهترین روشهای حمل مواد و طراح کارخانهها را تعیین میکنند.
مشتقات برای یافتن بیشینه و کمینهٔ یک تابع نیز به کار میروند. معادلات دربرگیرندهٔ مشتقات، معادلات دیفرانسیل نامیده میشوند و در توصیف پدیدههای طبیعی دارای اهمیت هستند. از مشتقات و تعمیم آنها در بسیاری از شاخههای ریاضیات، مانند آنالیز مختلط، آنالیز تابعی، هندسهٔ دیفرانسیل، نظریهٔ اندازه و جبر مجرد بهره برده میشود.
منابع
[ویرایش]ویکی پدیای فارسی
انتگرال
در ریاضیات، انتگرال ، روشی برای اختصاص اعداد به توابع است؛ به گونهای که جابجایی، مساحت، حجم و دیگر مفاهیم برآمده از ترکیب دادههای بینهایت کوچک را به وسیله آن بتوان توصیف کرد. انتگرالگیری یکی از دو عمل مهم در حساب دیفرانسیل و انتگرال است، که عمل دیگر آن(عمل معکوس) دیفرانسیلگیری یا همان مشتقگیری است. برای تابع داده شدهای چون f از متغیر حقیقی x و بازه از خط حقیقی،به صورت ساده و انتگرال معین نوشته می گردد:
بهطور صوری به عنوان مساحت علامتدار ناحیهای از صفحه xy که به نمودار f، محور x و خطوط عمودی x=a و x=b محدود شدهاست. نواحی بالای محور x به مساحت کل افزوده و نواحی پایین محور x از آن میکاهند.
عملیات انتگرالگیری، در حد یک مقدار ثابت (یعنی بدون در نظر گرفتن یک مقدار ثابت)، معکوس عملیات دیفرانسیلگیری است. بدین منظور، اصطلاح انتگرال را میتوان به معنای پاد-مشتق نیز به کار برد، یعنی تابعی چون F که مشتقش تابع داده شدهی f باشد. در این حالت به انتگرال f، انتگرال نامعین گفته شده و به صورت زیر نوشته میشود:
انتگرالهایی که در این مقاله مورد بحث قرار میگیرند از نوع انتگرال معین اند. قضیه اساسی حساب، دیفرانسیلگیری را به انتگرال معین ارتباط میدهد: اگر f یک تابع پیوسته حقیقی مقدار روی بازهٔ باشد، آنگاه زمانی که پاد مشتق f یعنی F، معلوم باشد، انتگرال f روی آن بازه مساوی است با:
اصول انتگرالگیری بهطور مستقل توسط اسحاق نیوتون و گوتفرید ویلهلم لایبنیز در اواخر قرن هفدهم میلادی قاعدهبندی شد، آنها انتگرال را به صورت جمع مستطیلهایی با عرضهای بینهایت کوچک میدیدند. برنارد ریمان تعریف دقیقی از انتگرال ارائه نمود. این تعریف بر اساس فرایند حد گیری است که مساحت زیر نمودار یک خم را با شکستن آن ناحیه به قطعات نازک عمودی تخمین میزند. با شروع قرن نوزدهم میلادی، مفاهیم پیچیدهتری از انتگرال ظهور پیدا کرد که در آن نوع تابع به علاوه دامنه انتگرالگیری تعمیم یافت. انتگرال خطی برای توابع دو یا چند متغیره تعریف شدهاست و بازه انتگرالگیری در آن با خمی که دو نقطه ابتدا و انتهای انتگرالگیری را به هم متصل میکند جایگزین شدهاست. در انتگرال سطح (یا انتگرال رویه ای)، خم با یک رویه در فضای سه بعدی جایگزین میشود.
تفاسیر
[ویرایش]انتگرال ها در بسیاری از موقعیت های عملی ظاهر می شوند. به عنوان مثال، از طول، عرض و عمق یک استخر شنا که مستطیل شکل با کف صاف است، می توان حجم آبی که می تواند داشته باشد، مساحت سطح و طول لبه آن را تعیین کرد. اما اگر بیضی شکل با پایین گرد باشد، برای یافتن مقادیر دقیق و دقیق برای این کمیت ها، انتگرال ها مورد نیاز است. در هر مورد، میتوان مقدار مورد نظر را به بینهایت قطعات بینهایت کوچک تقسیم کرد، سپس قطعات را جمع کرد تا به یک تقریب دقیق دست یافت.
به عنوان مثال، برای یافتن مساحت ناحیه محدود شده توسط نمودار تابع f ( x ) = √ x بین x = 0 و x = 1 ، می توان از فاصله در پنج مرحله عبور کرد ( 0، 1/5، 2/ 5، ...، 1 )، سپس با استفاده از ارتفاع سمت راست انتهای هر قطعه یک مستطیل را پر کنید (بنابراین √ 0 ، √ 1/5 ، √ 2/5 ، ...، √ 1 ) و مساحت آنها را جمع کنید تاتقریب از یک عدد به دست آید.که از مقدار دقیق آن بزرگتر است. از طرف دیگر، هنگام جایگزینی این زیر بازهها با یکی با ارتفاع انتهای سمت چپ هر قطعه، تقریبی که بدست میآید بسیار کم است: با دوازده زیر بازه، مساحت تقریبی فقط 0.6203 است. با این حال، زمانی که تعداد قطعات تا بی نهایت افزایش یابد، به حدی می رسد که مقدار دقیق مساحت مورد نظر است (در این مورد، 2/3یکی می نویسد)
تعاریف رسمی
[ویرایش]راه های زیادی برای تعریف رسمی یک انتگرال وجود دارد که همه آنها معادل نیستند. تفاوت ها عمدتاً برای رسیدگی به موارد خاص متفاوت وجود دارد که ممکن است تحت تعاریف دیگر قابل ادغام نباشند، اما گاهی اوقات به دلایل آموزشی نیز وجود دارد. متداول ترین تعاریف انتگرال ریمان و انتگرال لبگ هستند.
انتگرال ریمان
[ویرایش]انتگرال ریمان بر اساس مجموع توابع ریمان با توجه به پارتیشن های برچسب گذاری شده یک بازه تعریف می شود. یک پارتیشن برچسب گذاری شده از یک بازه بسته [ a , b ] روی خط واقعی یک دنباله محدود است.
این بازه [ a , b ] را به n بازه فرعی [ xi −1 ، xi ] که با i نمایه شده است تقسیم میکند، که هر کدام با یک نقطه متمایز t i ∈ [xi -1 ، x i ] « برچسب » شدهاند . . مجموع ریمان تابع f با توجه به چنین پارتیشن برچسبگذاری شده به صورت تعریف میشود
بنابراین هر جمله از مجموع مساحت یک مستطیل با ارتفاع برابر با مقدار تابع در نقطه متمایز از بازه فرعی داده شده، و عرض برابر با عرض فاصله فرعی، Δ i = x i - x i است. -1 . مش چنین پارتیشن برچسب گذاری شده ای عرض بزرگترین بازه فرعی است که توسط پارتیشن تشکیل شده است، max i = 1... n Δ i . انتگرال ریمان تابع f در بازه [ a , b ] برابر با S است اگر:
برای همهوجود داردباشد به طوری که برای هر[a,b] برچسب گذاری شده باشد کمتر از هنگامی که تگهای انتخابی حداکثر (به ترتیب، حداقل) مقدار هر بازه را میدهند، مجموع ریمان به جمع داربوکس بالایی (به ترتیب، پایینتر) تبدیل میشود که ارتباط نزدیک بین انتگرال ریمان و انتگرال داربو را نشان میدهد .
انتگرال لبگ
[ویرایش]غالباً چه در تئوری و چه در کاربردها، قابل توجه است که بتوان از حد انتگرال عبور کرد. برای مثال، اغلب میتوان دنبالهای از توابع را ساخت که به معنایی مناسب، راهحل یک مسئله را تقریب میکنند. سپس انتگرال تابع حل باید حد انتگرال تقریب ها باشد. با این حال، بسیاری از توابعی که می توان به عنوان حد به دست آورد، قابل انتگرال پذیری ریمان نیستند، و بنابراین چنین قضایای حدی با انتگرال ریمان سازگار نیستند. بنابراین، داشتن تعریفی از انتگرال که امکان ادغام کلاس وسیع تری از توابع را فراهم می کند، اهمیت زیادی دارد.
چنین انتگرالی انتگرال لبگ است که از واقعیت زیر برای بزرگتر کردن کلاس توابع انتگرالپذیر استفاده میکند: اگر مقادیر یک تابع در دامنه مرتب شوند، انتگرال یک تابع باید ثابت بماند. همانطور که فولاند میگوید، «برای محاسبه انتگرال ریمان f ، دامنه [ a , b ] را به زیر بازهها تقسیم میکنیم، در حالی که در انتگرال لبگ، «در واقع محدوده f را تقسیم میکنیم. بنابراین تعریف انتگرال لبگ با یک اندازه آغاز می شود ، μ. در ساده ترین حالت، اندازه گیری لبگ (μ ( A یک بازه [A = [ a , b عرض آن است، b − a، به طوری که انتگرال لبگ با انتگرال (مناسب) ریمان در زمانی که هر دو وجود دارند موافق است. در موارد پیچیدهتر، مجموعههایی که اندازهگیری میشوند میتوانند بسیار پراکنده باشند، بدون پیوستگی و هیچ شباهتی به فواصل.
با استفاده از فلسفه "تقسیم بندی محدوده f "، انتگرال یک تابع غیرمنفی f : R → R باید مجموع بیش از t مناطق بین یک نوار افقی نازک بین y = t و y = t + dt باشد. این ناحیه فقط μ { x : f ( x ) > t } dt است . فرض کنید f ∗ ( t ) = μ { x : f ( x) > t } . سپسfتوسط انتگرال لبگ تعریف می شود
جایی که انتگرال سمت راست یک انتگرال ریمان نامناسب معمولی است ( f ∗ یک تابع مثبت کاملاً کاهشی است و بنابراین دارای یک انتگرال ریمان نامناسب کاملاً تعریف شده است ). برای یک کلاس مناسب از توابع (توابع قابل اندازه گیری ) این انتگرال لبگ را تعریف می کند.
اگر مجموع مقادیر مطلق نواحی بین نمودار f و محور x محدود باشد، یک تابع قابل اندازهگیری کلی f ، قابل انتگرالپذیری لبگ است:
در آن صورت، انتگرال، مانند حالت ریمانی، تفاوت بین ناحیه بالای محور x و ناحیه زیر محور x است:
جایی که
خواص
[ویرایش]خطی بودن
[ویرایش]مجموعه توابع قابل ادغام ریمان در یک بازه بسته [ a , b ] یک فضای برداری را تحت عملیات جمع نقطه ای و ضرب توسط یک اسکالر و عملیات یکپارچه سازی تشکیل می دهد.
یک تابع خطی در این فضای برداری است. بنابراین، مجموعه توابع انتگرال پذیر با گرفتن ترکیبات خطی بسته می شود ، و انتگرال یک ترکیب خطی، ترکیب خطی انتگرال ها است:
به طور مشابه، مجموعه توابع انتگرال پذیر Lebesgue با ارزش واقعی در فضای اندازه گیری داده شده E با اندازه گیری μ تحت ترکیب های خطی بسته می شود و بنابراین یک فضای برداری و انتگرال لبگ را تشکیل می دهد.
یک تابع خطی در این فضای برداری است، به طوری که:
به طور کلی، فضای برداری همه توابع قابل اندازه گیری را در یک فضای اندازه گیری در نظر بگیرید ( E , μ ) و مقادیر را در یک فضای برداری توپولوژیکی کامل فشرده محلی V روی یک میدان توپولوژیکی فشرده محلی K ، f : E → V در نظر بگیرید. سپس می توان یک نقشه انتزاعی انتزاعی تعریف کرد که به هر تابع یک عنصر از V یا نماد ∞ اختصاص می دهد ،
که با ترکیبات خطی سازگار است. در این وضعیت، خطی بودن برای زیرفضای توابعی که انتگرال آنها عنصری از V است (یعنی "محدود") برقرار است. مهمترین موارد خاص زمانی به وجود میآیند که K R ، C یا یک گسترش متناهی از میدان Q p از اعداد پی آدیک باشد ، و V یک فضای برداری با بعد محدود روی K باشد، و زمانی که K = C و V یک مختلط است. فضای هیلبرت
خطی بودن، همراه با برخی ویژگیهای پیوستگی طبیعی و نرمالسازی برای کلاس خاصی از توابع «ساده»، ممکن است برای ارائه یک تعریف جایگزین از انتگرال استفاده شود. این رویکرد دانیل برای مورد توابع با ارزش واقعی در مجموعه X است که توسط نیکلاس بورباکی به توابع با مقادیر در یک فضای برداری توپولوژیکی فشرده محلی تعمیم داده شده است. برای توصیف بدیهی انتگرال به هیلدبراند 1953 مراجعه کنید .
نابرابری ها
[ویرایش]تعدادی از نابرابریهای کلی برای توابع قابل انتگرالپذیری ریمان که در بازههای بسته و محدود [ a , b ] تعریف شدهاند وجود دارند و میتوان آنها را به مفاهیم دیگر انتگرال تعمیم داد (لبگ و دانیل).
- مرزهای بالا و پایین. یک تابع انتگرال پذیر f در [ a , b ] ، لزوماً در آن بازه محدود است. بنابراین اعداد حقیقی m و M وجود دارند به طوری که m ≤ f ( x ) ≤ M برای همه x در [ a , b ] . از آنجایی که مجموع پایین و بالایی f بیش از [ a , b ] به ترتیب با m محدود می شوند ( b-a ) و M ( b − a ) ، نتیجه می شود که
- نابرابری بین توابع اگر f ( x ) ≤ g ( x ) برای هر x در [ a , b ] ، هر یک از مجموع بالا و پایین f در بالا به ترتیب با مجموع بالا و پایین g محدود می شود. بدین ترتیب
این تعمیم نابرابری های فوق است، زیرا M ( b - a ) انتگرال تابع ثابت با مقدار M بیش از [ a , b ] است. علاوه بر این، اگر نابرابری بین توابع دقیق باشد، نابرابری بین انتگرال ها نیز شدید است. یعنی اگر f ( x ) < g ( x ) برای هر x در [ a , b ]
- زیر بازه ها اگر [ c , d ] زیر بازه ای از [ a , b ] باشد و f ( x ) برای همه x غیر منفی باشد ، آنگاه
- محصولات و مقادیر مطلق توابع. اگر f و g دو تابع باشند، ممکن است حاصل ضربات نقطهای و توان و مقادیر مطلق آنها را در نظر بگیریم :
اگر f روی [ a , b ] قابل ادغام ریمان باشد ، در مورد نیز همینطور است| f | ، و
علاوه بر این، اگر f و g هر دو انتگرال پذیر ریمان باشند، fg نیز قابل انتگرال پذیری ریمان است، و
این نابرابری که به نام نابرابری کوشی-شوارتز شناخته میشود ، نقش برجستهای در نظریه فضای هیلبرت بازی میکند، جایی که سمت چپ به عنوان حاصلضرب درونی دو تابع مربعپذیر f و g در بازه [ a ، b ] تفسیر میشود .
- نابرابری هلدر فرض کنید که p و q دو عدد واقعی هستند، 1 ≤ p , q ≤ ∞ با1/پ+1/q= 1 و f و g دو تابع قابل ادغام ریمان هستند. سپس توابع | f | p و | g | q نیز انتگرال پذیر هستند و نابرابری هلدر زیر صادق است: برای p = q = 2 ، نابرابری هولدر به نابرابری کوشی-شوارتز تبدیل می شود.
- نابرابری مینکوفسکی فرض کنید که p ≥ 1 یک عدد واقعی است و f و g توابع قابل انتگرال گیری ریمان هستند. سپس | f | p , | g | p و | f + g | p همچنین قابل ادغام ریمان هستند و نابرابری مینکوفسکی زیر صادق است:
یک آنالوگ این نابرابری برای انتگرال لبگ در ساخت فضاهای L p استفاده می شود.
کنوانسیون ها
[ویرایش]در این بخش، f یک تابع قابل ادغام ریمان با ارزش واقعی است . انتگرال
در یک بازه [ a , b ] تعریف می شود اگر a < b . این بدان معنی است که مجموع بالا و پایین تابع f در یک پارتیشن a = x 0 ≤ x 1 ≤ ارزیابی می شود. . . ≤ x n = b که مقادیر x i در حال افزایش است. از نظر هندسی، این نشان میدهد که ادغام از چپ به راست انجام میشود و f را در فواصل زمانی [ xi ، x i +1 ] ارزیابی میکند . جایی که یک بازه با شاخص بالاتر در سمت راست یک با شاخص کمتر قرار دارد. مقادیر a و b ، نقاط انتهایی بازه ، حدود یکپارچه سازی f نامیده می شوند . انتگرال ها همچنین می توانند تعریف شوند اگر a > b :
با a = b ، این نشان می دهد:
اولین قرارداد با توجه به در نظر گرفتن انتگرال ها بر فرعی بازه های [ a , b ] ضروری است . دومی می گوید که انتگرال گرفته شده در یک بازه منحط، یا یک نقطه ، باید صفر باشد . یکی از دلایل قرارداد اول این است که انتگرال پذیری f در بازه [ a , b ] دلالت بر این دارد که f در هر زیر بازه [ c , d ] قابل انتگرال است، اما به طور خاص انتگرال ها این ویژگی را دارند که اگر c هر عنصری از [ a باشد. ،b ] ، سپس:
با اولین قرارداد، رابطه حاصل
سپس برای هر جایگشت چرخه ای a ، b و c به خوبی تعریف می شود .
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
محتوای این صفحه در حال تحقیق است.
انتگرال سری فوریه
انتگرال سری فوریه،نوعی انتگرال است که موارد سری فوریه پیچیده را بااستفاده از انتگرال بدست می آید.انتگرال سری فوریه موارد های نامتناهی پیچیده که به صورت تابعی وبه صورت مثلثاتی است را با آنالیز،انتگرال جز به جز و به صورت محاسبه الگوی متناهی و نامتناهی، محاسبه می کند.این انتگرال پیشرفته تر از انتگرال فوریه است،در اینجا عددپی به صورت رادیان محاسبه می گردد البته انتگرال سری فوریه به صورت آنالیز فوریه نیز عمل می کند.
این موضوع را می توان گفت که ادامه مبحث بزرگ علم سری فوریه است که با نام انتگرال گیری سری فوریه،سری فوریه و انتگرال نیز هم گفته می شود.
مثال
[ویرایش]نمونه مثال
[ویرایش]سری فوریه تابعی(f(xبرابرباx2است که در آنxکوچکتر از2π و بزرگتر از0 است را محاسبه کنید و حاصل عبارت را بدست آورید
حل
[ویرایش]ابتدا تابعی را می کشیم که به صورت تابعx^2است بعد مسافت طول تابع را عدد2πمی گوییم و ارتفاع آن با محاسبه به4π2می رسیم.
در اینجا به روش دیریکله می رویم.
دوره تناوب=2π
چون دروه تناوب برابربا2πاست پس نصع دوره تناوب که عددLاست برابر باπاست پس(L=π)است
حالا ما به روش انتگرال دوره تناوب را بدست می آوریم.دوره تناوب که بدست آمد سری فوریه با انتگرال به صورت جز به جز می نویسیم.ابتدا از کسینوس شروع می کنیم
بعد اینگونه می نویسیم.چون در اینجا مسئله ازnحرف زده استnرا به صورت کسری درxضرب می کنیم تا سری فوریه برقرار باشد.ابتدا انتگرال گیری جز به جز را محاسبه و بعد رابطه نویسی می کنیم.بعد به انتگرال جز به جز سینوس می رسیم.
ابتدا انتگرال گیری جز به جز را محاسبه و بعد رابطه نویسی می کنیم.دراینجا کار تمام می شود و رابطه نویسی کامل می کنیم.در اینجا دوره تناوب در تابع نصف می گرد تا حد تناهی باهم منطبق گرددبرای محاسبه اگرx=0،2π جواب باهم برابر است که اینگونه می گرد
براساس معادله بدست می آید
این طرفین با تقسیم بر چهار مقدار بدست می آید که برابر است با:
منابع
[ویرایش]تحقیقی از ویکی پدیای فارسی
math.stackexchange.com https://math.stackexchange.com › ... Integration and differentiation of Fourier series
سری فوریه
سری فوریه بسطی است که هر تابع متناوب را به صورت حاصل جمع تعدادی نامتناهی از توابع نوسانی ساده (سینوسی، کسینوسی یا تابع نمایی مختلط) بیان میکند. این تابع به نام ریاضیدان بزرگ فرانسوی، ژوزف فوریه نامگذاری شدهاست. با بسط هر تابع به صورت سری فوریه، مولفههای بسامدی آن تابع به دست میآید.
یکی دیگر از تکنیک های تحلیل (که در اینجا به آن پرداخته نمی شود)، مناسب برای توابع دوره ای و غیر تناوبی، تبدیل فوریه است که یک پیوستار فرکانس از اطلاعات مؤلفه را ارائه می دهد. اما وقتی برای یک تابع تناوبی اعمال می شود، همه اجزاء دارای دامنه صفر هستند، به جز در فرکانس های هارمونیک. تبدیل فوریه معکوس یک فرآیند سنتز است (مانند سری فوریه)، که اطلاعات مؤلفه (اغلب به عنوان نمایش دامنه فرکانس شناخته می شود) را به بازنمایی حوزه زمانی خود تبدیل می کند. از زمان فوریه، رویکردهای مختلفی برای تعریف و درک مفهوم سری فوریه کشف شده است که همگی با یکدیگر همخوانی دارند، اما هر کدام بر جنبه های مختلف موضوع تأکید دارند. برخی از رویکردهای قدرتمندتر و ظریفتر مبتنی بر ایدهها و ابزارهای ریاضی هستند که در زمان فوریه در دسترس نبودند. فوریه در ابتدا سری فوریه را برای توابع با ارزش واقعی آرگومان های واقعی تعریف کرد و از توابع سینوس و کسینوس به عنوان مجموعه پایه برای تجزیه استفاده کرد. بسیاری از تبدیلهای مرتبط با فوریه از آن زمان تعریف شدهاند و ایده اولیه او را به بسیاری از کاربردها گسترش داده و حوزهای از ریاضیات به نام تحلیل فوریه را ایجاد کردهاند.
تاریخچه
[ویرایش]سری فوریه به افتخار ژان باپتیست ژوزف فوریه (1768-1830) نامگذاری شده است، که پس از تحقیقات اولیه توسط لئونارد اویلر، ژان لو روند دالامبر و دانیل برنولی، سهم مهمی در مطالعه سریهای مثلثاتی داشت. فوریه این مجموعه را با هدف حل معادله گرما در یک صفحه فلزی معرفی کرد و نتایج اولیه خود را در سال 1807 در کتاب خاطرات انتشار گرما در اجسام جامد (رساله انتشار گرما در اجسام جامد) منتشر کرد. Théorie analytique de la chaleur (نظریه تحلیلی گرما) او در سال 1822. Mémoire تجزیه و تحلیل فوریه، به ویژه سری فوریه را معرفی کرد. از طریق تحقیقات فوریه، این واقعیت ثابت شد که یک تابع دلخواه (در ابتدا، پیوسته و بعداً به هر قطعه ای-صاف تعمیم داده شد) را می توان با یک سری مثلثاتی نشان داد. اولین اعلام این کشف بزرگ توسط فوریه در سال 1807 و قبل از آکادمی فرانسه صورت گرفت. ایدههای اولیه تجزیه یک تابع تناوبی به مجموع توابع نوسانی ساده به قرن سوم قبل از میلاد برمیگردد، زمانی که ستارهشناسان باستان یک مدل تجربی از حرکات سیارهای را بر اساس دفرنتها و epicycles پیشنهاد کردند. معادله گرما یک معادله دیفرانسیل جزئی است. قبل از کار فوریه، هیچ راه حلی برای معادله گرما در حالت کلی شناخته نشده بود، اگرچه اگر منبع گرما به روشی ساده رفتار می کرد، به ویژه اگر منبع گرما یک موج سینوسی یا کسینوس بود، راه حل های خاصی شناخته شدند. این راه حل های ساده اکنون گاهی اوقات راه حل های ویژه نامیده می شوند. ایده فوریه این بود که یک منبع گرمایی پیچیده را به عنوان یک برهم نهی (یا ترکیب خطی) از امواج ساده سینوسی و کسینوس، و نوشتن راه حل به عنوان برهم نهی از محلول های ویژه مربوطه، مدل کند. این برهم نهی یا ترکیب خطی سری فوریه نامیده می شود. از دیدگاه مدرن، نتایج فوریه تا حدودی غیر رسمی هستند، به دلیل فقدان مفهوم دقیق عملکرد و انتگرال در اوایل قرن نوزدهم. بعداً، پیتر گوستاو لژون دیریکله و برنهارد ریمان نتایج فوریه را با دقت و رسمی بیشتری بیان کردند. اگرچه انگیزه اصلی حل معادله گرما بود، اما بعداً مشخص شد که تکنیکهای مشابه را میتوان برای طیف گستردهای از مسائل ریاضی و فیزیکی، و بهویژه آنهایی که شامل معادلات دیفرانسیل خطی با ضرایب ثابت هستند، به کار برد، که حلهای ویژه برای آنها سینوسی هستند. سری فوریه کاربردهای زیادی در مهندسی برق، تحلیل ارتعاش، آکوستیک، اپتیک، پردازش سیگنال، پردازش تصویر، مکانیک کوانتومی، اقتصاد سنجی،نظریه پوسته،و... دارد.
تعریف
[ویرایش]پیش گفتار
[ویرایش]توابع مورد استفاده در مهندسی و توابع نمایانگر سیگنالها معمولاً توابعی از زمان هستند یا به عبارت دیگر توابعی که در میدان زمان تعریف شدهاند. برای حل بسیاری از مسائل بهتر است که تابع در دامنه فرکانس تعریف شده باشد؛ زیرا این دامنه ویژگیهایی دارد که به راحتی محاسبات میانجامد.
فرض کنید که تابعی به شکل زیر تعریف شدهاست:
که در آن یک عدد صحیح مثبت، دامنه، بسامد و فاز توابع کسینوسی میباشد. قابل مشاهده است که با در دست داشتن بسامدها ، دامنهها و فازها تابع بهطور کامل قابل تعریف است. توجه شود که بر اساس گفتههای بالا تابع مستقل از زمان قابل تعریف است.
نمایشهای مختلف سری فوریه
[ویرایش]نمایش مثلثاتی
[ویرایش]اگر یک تابع متناوب با دوره تناوب باشد (یا به عبارتی: ) آنگاه این تابع را میتوان به صورت زیر نوشت:
که در آن هارمونیک nام سری فوریه با رادیان بوده و ضرایب ، و را میتوان از فرمولهای اویلر بدست آورد.
فوریه بر این باور بود که هرگونه تابع متناوب را میتوان به صورت جمعی از توابع سینوسی نوشت. این مطلب درست نیست. شرایط لازم برای هر تابع متناوب برای اینکه به صورت سری فوریه نوشته شود به صورت زیر است:
- تابع در هر دورهٔ تناوبی انتگرال پذیر باشد:
- تابع فقط شمار محدودی بیشینه و کمینه داشته باشد.
- تابع فقط شمار محدودی ناپیوستگی داشته باشد.
نمایش مختلط
[ویرایش]سری فوریه میتواند به صورت زیر نیز نوشته شود:
و در اینجا:
این رابطه با کمک فرمول اویلر قابل گسترش به صورت زیر است:
اگر این رابطه را بهطور مستقیم با نمایش مثلثی مقایسه کنیم مشاهده میشود که به طریق زیر نیز قابل محاسبه است:
نمایش کسینوس-با-فاز
[ویرایش]نمایش زیر که در واقع شکل ویژهای از نمایش مثلثی میباشد، نمایش کسینوس-با-فاز نام دارد. از این نمایش در رسم طیف خطی استفاده میشود.
محاسبه ضرایب فوریه
[ویرایش]نمایش مثلثی
[ویرایش]نمایش مثلثی بالا را در نظر بگیرید. همانطور که گفته شد دوره تناوب و هارمونی nام تابع میباشد. در تبدیل فوریه سه ضریب و و ضریب ثابت مطرح است. ضریبها با استفاده از روابط زیر قابل محاسبه هستند.
بازه [-] یا در کل بازههایی که طول آنها است از مهمترین بازههایی است که درمحاسبه ضرایب استفاده میشود. بدین ترتیب پس ضرایب عبارتند از:
همگرایی
[ویرایش]در کاربردهای مهندسی، بهطور کلی فرض میشود که سریهای فوریه تقریباً در همه جا همگرا شوند (استثنائاتی در ناپیوستگیهای گسسته وجود دارد) زیرا عملکردهایی که در مهندسی مشاهده میشوند رفتار بهتری نسبت به توابعی دارند که ریاضیدانان میتوانند به عنوان نمونههای متضاد این فرض ارائه دهند. بهطور خاص، اگر پیوسته باشد و مشتق (که ممکن است در همه جا وجود نداشته باشد) مربع انتگرال دار است، پس سریهای فوریه بهطور کامل و یکنواخت به همگرا میشوند.
-
چهار جمع جزئی (سری فوریه) با طول ۱ ، ۲ ، ۳ و ۴ جمله ای، که نشان میدهد چگونه تقریب با یک موج مربعی با افزایش تعداد جملهها بهبود مییابد.
-
چهار مجموع جزئی (سری فوریه) با طول ۱ ، ۲ ، ۳ و ۴ جمله ای، که نشان میدهد چگونه تقریب با یک موج دندانه اره ای با افزایش تعداد جملهها بهبود مییابد.
-
نمونه ای از همگرایی به یک تابع نسبتاً دلخواه. به شکلگیری "طنین" (پدیده گیبس) در انتقال به بخشهای عمودی توجه کنید.
توابع با ارزش پیچیده
[ویرایش]اگریک تابع با ارزش پیچیده از یک متغیر واقعی استهر دو مؤلفه (قسمت واقعی و خیالی) توابعی با ارزش واقعی هستند که می توانند با یک سری فوریه نمایش داده شوند. دو مجموعه ضرایب و مجموع جزئی به صورت زیر به دست می آیند :
- و
- به صورت زیر نوشته می گردد
تعریف کردنبازده:
این با معادله 5 یکسان است به جزودیگر مزدوج پیچیده نیستند. فرمول برایهمچنین بدون تغییر است:
سایر نمادهای رایج
[ویرایش]نمادبرای بحث در مورد ضرایب فوریه چندین تابع مختلف کافی نیست. بنابراین، معمولاً با یک شکل تغییر یافته از تابع (، در این مورد) مانندیاو نماد عملکردی اغلب جایگزین اشتراک می شود:
در مهندسی، به ویژه زمانی که متغیرنشان دهنده زمان است، دنباله ضریب نمایش دامنه فرکانس نامیده می شود . از براکت های مربعی اغلب برای تاکید بر اینکه دامنه این تابع مجموعه ای گسسته از فرکانس ها است استفاده می شود.
یکی دیگر از نمایش های رایج حوزه فرکانس از ضرایب سری فوریه برای تعدیل یک شانه دیراک استفاده می کند :
جایی کهfیک دامنه فرکانس پیوسته را نشان می دهد. وقتیxمتغیر است و واحدهای ثانیه دارد،fدارای واحدهای هرتز است. «دندانهای» شانه در چند برابر (یعنی هارمونیک ) فاصله دارندکه به آن فرکانس بنیادی می گویند.می توان از این نمایش با تبدیل فوریه معکوس بازیابی کرد :
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای فارسی
تبدیل فوریه
تبدیل فوریه یک تبدیل ریاضی است که توابع در زمان یا مکان را به توابعی در فرکانس زمانی یا مکانی تجزیه می کند، مانند بیان یک آکورد موسیقی بر حسب حجم و فرکانس نت های تشکیل دهنده آن. اصطلاح تبدیل فوریه هم به نمایش حوزه فرکانس و هم به عملیات ریاضی مربوطه اشاره دارد که نمایش دامنه فرکانس را به تابعی از فضا یا زمان مرتبط میکند.

تعریف
[ویرایش]در تبدیل فوریه اگر تابعی به اسمf داشته باشیم و این تابع انتگرال پذیر باشد و به صورتباشد و حد بی نهایت منفی و مثبت داشته باشیم به این صورت است
تبدیل تابع در فرکانس با عدد مختلط داده میشود. ارزیابی برای همه مقادیر تابع frequency-domain را تولید می کند. تبدیل فوریه در اینجا با افزودن یک circumflex به نماد تابع نشان داده می شود. وقتی متغیر مستقل time را نشان می دهد (اغلب به جای با نشان داده می شود)، متغیر تبدیل نشان دهنده فرکانس است (اغلب با به جای ). به عنوان مثال. اگر زمان با ثانیه اندازهگیری شود، فرکانس بر حسب هرتز است.
تبدیل فوریه که از نام ریاضیدان فرانسوی جوزف فوریه نامگذاری شده است
، تبدیلی انتگرالی است که در آن هر تابعبه تابع دیگری منعکس می کند. در این مورد، به تابع "تبدیل فوریه" می گویند. حالت ویژه تبدیل فوریه سری فوریه نامیده می شود و زمانی استفاده می شود که تابع متناوب باشد، یعنی: . اگر تابع متناوب نباشد، یا به عبارت دیگر، تناوب آن برابر با بی نهایت () است، از سری فوریه عبارت زیر به دست می آید:
تبدیل فوریه و همراه با آن آنالیز فوریه در مباحث مختلف فیزیک از جمله الکترونیک و الکترومغناطیسی (به ویژه در مخابرات)، آکوستیک، فیزیک امواج و غیره کاربرد فراوانی دارد.
منابع
[ویرایش]تحقیق از طریق منابع های ویکی پدیای فارسی
ویکی پدیای انگلیسی
معادله لاپلاس
معادله لاپلاس یک معادله دیفرانسیل با مشتقات جزئی است که بسیار مهم است و در ریاضیات، فیزیک و مهندسی کاربرد دارد. به عنوان نمونه می توان به رشته هایی مانند الکترومغناطیس، نجوم و دینامیک سیالات اشاره کرد که در آنها از حل این معادله استفاده شده است. می توان آن را به صورت سه بعدی به صورت زیر نمایش داد:

تعریف
[ویرایش]در فضای سه بعدی، مسئله پیدا کردن تابع حقیقی دو بار مشتقپذیر φ بر حسب متغیرهای y ,x و z است بطوریکه: در مختصات دکارتی:
در مختصات استوانهای:
در مختصات کروی:
و در مختصات خمیدهخط:
یا:
این معادله غالباً به صورت زیر نوشته میشود:
یا در متون عمومی بصورت:
که در آن 2∇=Δ عملگر لاپلاس یا لاپلاسین است.
جایی که div=. ∇ واگرایی و grad=∇ گرادیان است. جواب های معادله لاپلاس را تابع هارمونیک می نامند. اگر در سمت راست به جای صفر یک تابع سه متغیری (f(x,y,z داشته باشیم:
این معادله معادله پواسون نامیده می شود. معادله لاپلاس و پواسون ساده ترین نمونه معادلات دیفرانسیل جزئی بیضوی هستند. عملگر دیفرانسیل جزئی یا (که ممکن است در هر بعد تعریف شود) عملگر لاپلاس نامیده می شود.
شرایط مرزی
[ویرایش]مسئله دیریکله برای معادله لاپلاس شامل یافتن جواب φ در برخی از حوزه های D است به طوری که φ در مرز D برابر با برخی از تابع های داده شده باشد. از آنجایی که عملگر لاپلاس در معادله گرما ظاهر میشود ، یک تفسیر فیزیکی از این مسئله به شرح زیر است: درجه حرارت را بر روی مرز دامنه مطابق با مشخصات داده شده شرط مرزی ثابت کنید. اجازه دهید گرما جریان یابد تا زمانی که به حالت ساکنی برسد که در آن دما در هر نقطه از دامنه دیگر تغییر نکند. سپس توزیع دما در فضای داخلی با حل مسئله دیریکله مربوطه داده می شود.
شرایط مرزی نویمان برای معادله لاپلاس نه تابع φ در مرز D بلکه مشتق نرمال آن را مشخص می کند. از نظر فیزیکی، این مربوط به ساخت یک پتانسیل برای یک میدان برداری است که اثر آن تنها در مرز D شناخته شده است. برای مثال معادله گرما، به معنای تجویز شار گرما از طریق مرز است. به طور خاص، در یک مرز آدیاباتیک، مشتق نرمال φ صفر است.
راه حل های معادله لاپلاس را توابع هارمونیک می نامند . همه آنها در حوزه ای که معادله در آن برآورده می شود، تحلیلی هستند. اگر هر دو تابع جواب معادله لاپلاس (یا هر معادله دیفرانسیل همگن خطی) باشند، مجموع آنها (یا هر ترکیب خطی) نیز جواب است. این ویژگی که اصل برهم نهی نامیده می شود بسیار مفید است. به عنوان مثال، راه حل های مسائل پیچیده را می توان با جمع کردن راه حل های ساده ساخت.
معادلات لاپلاس در دو بعد
[ویرایش]فرم معادلهٔ لاپلاس با دو متغیر مستقل به صورت زیر است:
توابع تحلیلی
[ویرایش]قسمت حقیقی و موهومی یک تابع تحلیلی مختلط، هر دو در معادله لاپلاس صدق میکند. اگر z مختلط باشد و: شرط لازم برای اینکه (f(z تابع تحلیلی باشد این است که در معادلهٔ کوشی ریمان صدق کند.
این منجر میشود به:
بنابراین u در معادلهٔ لاپلاس صدق میکند. به همین شکل میتوان نشان داد که v هم در معادلهٔ لاپلاس صدق میکند. بالعکس، با در نظر گرفتن یک تابع هارمونیک، بخش تحلیلی (f(z (حداقل بهطور موضعی) است اگر آزمون به فرم
باشد، در صورتی که قرار دهیم:
- .
معادله کوشی ـ ریمان ارضا میشود. این رابطه ψرا مشخص نمیکند، بلکه فقط رشد آن را مشخص میکند.
معادله لاپلاس برای ψ بهطور ضمنی بیان میکند که شرایط انتگرالپذیری در ψ صدق میکند.
و بنابراین ψ را میتوان با یک انتگرال خط تعریف کرد. شرایط انتگرالپذیری و قضیه استوکس نشان میدهد که مقدار انتگرال تنها به دو نقطه ابتدایی و انتهایی ارتباط دارد و از مسیر مستقل است. جفت جوابهای معادله لاپلاس توابع همساز همیوغ نامیده میشوند. این نتیجه تنها هنگامی که مسیر دور یک نقطه تکین دور نزند و بهطور موضعی مورد قبول است. برای مثال اگر r و v مختصات قطبی باشند
یک تابع تحلیلی معادل است با
در هر صورت زاویهٔ θ فقط در ناحیهای که مبدأ را محصور نمیکند تک مقداری است. رابطه نزدیک بین معادله لاپلاس و تابع تحلیلی نشان میدهد که هر جواب معادله لاپلاس از هر مرتبهای مشتق دارد و حداقل در یک دایره که یک نقطهٔ تکین را محصور نکند میتواند به صورت یک سری توانی بسط داده شود. این با جواب معادلهٔ موج کاملاً در تضاد است، که معمولاً نظم کمتری دارد. یک رابطهٔ نزدیک بین سریهای توانی و سریهای فوریه وجود دارد. اگر ما یک تابع f را به صورت سری توانی در یک دایره با شعاع R بسط دهیم، این به این معناست که
ضرایب تعریف شده مناسب قسمتهای موهومی و حقیقی به این صورت دارند:
بنابراین
که فرمول بالا، یک سری فوریه برای f است.
شارش سیال
[ویرایش]فرض کنیم u و v مؤلفههای عمودی و افقی سرعت یک سیال تراکم ناپذیر و غیر چرخشی در فضای دو بعدی باشد. شرط اینکه سیال تراکمناپذیر باشد به این صورت است که
و شرط اینکه سیال غیر چرخشی باشد:
اگر ما دیفرانسیل تابع ψرابه این صورت در نظر بگیریم:
در این صورت شرط تراکمناپذیری، شرط انتگرالپذیری برای این دیفرانسیل است. تابع حاصل، تابع جریان نامیده میشود، چون که در راستای شارش ثابت است. مشتق اول ψ به صورت زیر داده میشود:
و شرط غیر چرخشی بودن اشاره به این دارد که، ψ در معادله لاپلاس صدق میکند. تابع همساز φ که همیوغ ψ است، «پتانسیل سرعت» نامیده میشود. معادله کوشی ـ ریمان بیان میکند که:
بنابراین هر تابع تحلیلی با یک شارش سیال تراکمناپذیر و پایدار و غیر چرخشی در صفحه مرتبط است. بخش حقیقی «پتانسیل سرعت» و بخش موهومی، «تابع جریان» است.
الکترواستاتیک
[ویرایش]با توجه به معادله ماکسول، یک میدان الکتریکی (u,v) در فضای دو بعدی که مستقل از زمان است در این معادلات صدق میکند:
و
جایی که ρ چگالی بار باشد. اولین معادله ماکسول، شرط انتگرالپذیری برای دیفرانسیل زیر است:
پس پتانسیل الکتریکی φ به گونهای ساخته میشود که شرایط زیر را ارضا نماید:
دومین معادله ماکسول دلالت دارد بر
که این معادله پواسون است.
معادله لاپلاس در فضای سه بعدی
[ویرایش]جواب اساسی
[ویرایش]یک جواب بنیادی معادله لاپلاس، در این رابطه صدق میکند:
جایی که تابع دلتای دیراک، نشان دهنده وجود یک واحد منبع در نقطهٔ است. هیچ تابعی این خاصیت را ندارد، اما میتوان آن را به عنوان حدی از توابعی که انتگرال آنها در فضا واحد است و پشتیبان (ناحیهای که تابع در آن صفر نیست) آنها به یک نقطه تبدیل شدهاست، در نظر گرفت. پس تعریف جواب اصلی اشاره دارد بر اینکه اگر از لاپلاسی u بر هر حجمی که نقطهٔ منبع را محصور کند، انتگرال بگیریم، داریم:
معادله لاپلاس تحت یک دوران مختصات ناوردا است و از این رو ما انتظار داریم که که جواب اصلی فقط به فاصلهٔ r از نقطه مبدأ بستگی داشته باشد. اگر ما حجم را به صورت کرهای با شعاع a حول نقطه منبع انتخاب کنیم، قضیه دیورژانس گاوس بیان میکند که:
این منجر میشود به
روی یک کره به شعاع r حول نقطهٔ منبع است و از این رو
یک استدلال مشابه نشان میدهد که در دو بعد این جواب این گونه است:
تابع گرین
[ویرایش]یک تابع گرین یک جواب اصلی است که شرایط مناسبی در مرز s از حجم v را ارضا میکند. برای مثال تابع گرین در این معادله صدق میکند.
اکنون اگر u یکی از جوابهای معادلهٔ پواسون در v باشد
و فرض میکنیم که u مقدار مرزی g روی s باشد. آنگاه ما فرمول گرین (یک نتیجه از قضیه دیورژانس) را بکار میبریم، که بیان میکند:
علائم un و Gn نشاندهنده مشتق نرمال بر s هستند. با در نظر گرفتن شرایط ارضا شده توسط U و G، این نتیجه به این رابطه ساده میشود:
بنابراین تابع گرین تأثیر دادههای f و g را در نقطه توضیح میدهد. در مورد داخل کرهای با شعاع a تابع گرین بهوسیلهٔ انعکاس، پیدا میشود. نقطه منبع p که در فاصله ρ از مبدأ کره قرار دارد در طول خط واصل این دونقطه، به یک نقطه 'p که در فاصله زیر قرار دارد، انعکاس پیدا میکند:
توجه کنید که اگر p در داخل کره باشد 'p در خارج کره خواهد بود. تابع گرین به این صورت داده میشود.
جایی که R فاصله تا نقطهٔ منبع p و 'R فاصله تا نقطه انعکاسی 'p را نشان میدهد. یک نتیجه از این عبارت برای تابع گرین، فرمول انتگرال پواسون است. فرض کنیم ρ و θ و φ مختصات کروی برای نقطه منبع p باشند. در اینجا θ نشاندهنده زاویه با محور عمودی است، که در تضاد با نشانه گذاری ریاضی آمریکایی معمولی است، اما با استاندارد اروپا و روال فیزیکی منطبق است. جواب معادله لاپلاس درون کره برابر است با
جایی که:
یک نتیجه ساده از این فرمول این است که اگر u یک تابع همساز باشد، مقدار u در مرکز کره برابر مقدار میانگین مقدارهای آن بر سطح کره است. این خاصیت مقدار میانگین فوراً نشان میدهد که یک تابع همساز غیر ثابت نمیتواند مقدار ماکزیمم خود را در یک نقطهٔ داخلی بگیرد.
منابع
[ویرایش]ویکی پدیای فارسی
تبدیل لاپلاس
تبدیل لاپلاس در ریاضیات یک تبدیل انتگرالی است که بسیار پرکاربرد است. تبدیل لاپلاس با نماد در واقع عملگری خطی از تابع (f (t با آرگومان حقیقی (t (t ≥ ۰ به تابع (F (s با آرگومان مختلط s است. در بسیاری از کاربردهای عملی، این تبدیل به صورت دوسویه عمل میکند. ویژگی مهم این تبدیل آن است که بسیاری از رابطهها و تغییراتی که بر روی تابع اصلی (f (t برقرار هستند، در تبدیل یافتهٔ آن (F (s نیز با رابطهای ساده و منطقی برقراراند.

تبدیل لاپلاس شبیه تبدیل فوریه است، با این تفاوت که تبدیل فوریه یک تابع را به حالتهای ارتعاشی آن تجزیه میکند، در حالی که تبدیل لاپلاس آن را به لحظههای خود تجزیه میکند. هر دو تبدیل لاپلاس و فوریه برای حل معادلات دیفرانسیل و انتگرال استفاده می شود. در فیزیک و مهندسی، این تبدیل برای تجزیه و تحلیل سیستمهای تغییرناپذیر زمان مانند مدارهای الکتریکی، ابزارهای نوری و سیستمهای مکانیکی استفاده میشود.در بیشتر موارد، تبدیل لاپلاس برای تبدیل سیستمهایی با ورودیها و خروجیهای وابسته به زمان به سیستمهای پیچیده وابسته به فرکانس زاویهای با واحدهای رادیان در واحد زمان استفاده میشود. به عبارت دیگر، اگر سیستمی را در نظر بگیریم که دارای توصیف ریاضی یا تابع ورودی و خروجی آن است، تبدیل لاپلاس آن به ما کمک می کند تا تابع جایگزینی را پیدا کنیم که تحلیل رفتار این تابع را آسان تر می کند.
روش تبدیل لاپلاس یک روش عملیاتی است که می تواند در حل معادلات دیفرانسیل خطی مفید باشد. با کمک تبدیل لاپلاس، بسیاری از توابع رایج مانند توابع سینوسی، توابع سینوسی میرا شده و توابع نمایی را می توان به توابع جبری با یک متغیر مختلط تبدیل کرد. عملیات جبری در صفحات پیچیده می تواند جای عملیاتی مانند مشتق و انتگرال را بگیرد. بنابراین، یک معادله دیفرانسیل خطی را می توان به یک معادله جبری با یک متغیر مختلط تبدیل کرد. سپس حل معادله دیفرانسیل را می توان با کمک جدول تبدیل لاپلاس یا روش تجزیه به کسرهای ساده بدست آورد.
یکی از مزایای روش تبدیل لاپلاس این است که امکان استفاده از روش های گرافیکی برای پیش بینی عملکرد سیستم را بدون حل واقعی معادلات دیفرانسیل سیستم فراهم می کند. مزیت دیگر این است که با حل معادله دیفرانسیل، هم مولفه گذرا و هم حالت پایدار راه حل را می توان همزمان بدست آورد.
پیشنیه تبدیل لاپلاس
[ویرایش]تبدیل لاپلاس به افتخار ریاضیدان و ستاره شناس فرانسوی پیر لاپلاس نامگذاری شده است. او اولین بار در یکی از آثارش در مورد نظریه احتمال از این تبدیل استفاده کرد. از سال 1744، لئونارد اویلر شروع به تحقیق در مورد انتگرال هایی به شکل زیر کرد:
او از این تبدیل برای حل معادلات دیفرانسیل استفاده کرد، اما آن را بیشتر در این زمینه دنبال نکرد. جوزف لوئیس لاگرانژ از جمله کسانی بود که تحت تأثیر اویلر قرار گرفت، در مطالعات خود در مورد ادغام تابع چگالی احتمال، روابطی به شکل زیر به دست آورد:
برخی از مورخان مدرن آن را با نام نظریه تبدیل لاپلاس جدید ذکر کرده اند. به نظر می رسد که این انتگرال ها برای اولین بار توسط لاپلاس در سال 1782 مورد توجه قرار گرفت. در سال 1785، او گام اصلی را به جلو برداشت و به جای اینکه تنها به دنبال راه حلی یکپارچه باشد، سعی کرد تغییرات لازم را در خود تحول ایجاد کند. او ابتدا از یک انتگرال با شکل زیر استفاده کرد:
منطقه همگرایی
[ویرایش]اگر f یک تابع انتگرالپذیر محلی باشد (یا به طور کلی یک اندازهگیری بورل به صورت محلی برای تغییرات محدود)، آنگاه تبدیل لاپلاس (F (s از f همگرا میشود به شرطی که حد وجود دارد. اگر انتگرال باشد، تبدیل لاپلاس کاملاً همگرا می شود به عنوان یک انتگرال لبگ مناسب وجود دارد. تبدیل لاپلاس معمولاً به صورت مشروط همگرا درک می شود ، به این معنی که به معنای اولی همگرا می شود اما در معنای دوم نیست. مجموعه مقادیری که (F (s برای آنها مطلقاً همگرا می شود یا به شکل Re(s) > a یا Re(s) ≥ a است، که در آن a یک ثابت واقعی بسط یافته با −∞ ≤ a ≤ ∞ است (نتیجه قضیه همگرایی غالب ). ثابت a به عنوان آبسیسا همگرایی مطلق شناخته می شود و به رفتار رشد (f (t بستگی دارد . به طور مشابه، تبدیل دو طرفه کاملاً در یک نوار از شکل همگرا می شود. a <Re(s) < b ، و احتمالاً شامل خطوط Re(s) = a یا Re(s) = b باشد. زیر مجموعه مقادیر s که تبدیل لاپلاس برای آنها به طور مطلق همگرا می شود، ناحیه همگرایی مطلق یا حوزه همگرایی مطلق نامیده می شود. در حالت دو طرفه، گاهی به آن نوار همگرایی مطلق می گویند. تبدیل لاپلاس در منطقه همگرایی مطلق تحلیلی است: این نتیجه قضیه فوبینی و قضیه موررا است .
به طور مشابه، مجموعه مقادیری که F ( s ) برای آنها همگرا می شود (شرط یا مطلق) به عنوان منطقه همگرایی شرطی یا به سادگی منطقه همگرایی (ROC) شناخته می شود. اگر تبدیل لاپلاس (به صورت مشروط) در s = s 0 همگرا شود، آنگاه به طور خودکار برای همه s با Re( s ) > Re( s 0 ) همگرا می شود . بنابراین، منطقه همگرایی یک نیم صفحه به شکل Re( s ) > a است، که احتمالاً شامل برخی از نقاط خط مرزی Re( s ) = a است.
در ناحیه همگرایی Re( s ) > Re( s 0 ) ، تبدیل لاپلاس f را می توان با ادغام با قطعات به عنوان انتگرال بیان کرد.
یعنی، F ( s ) را می توان به طور موثر در ناحیه همگرایی، به عنوان تبدیل لاپلاس کاملا همگرا یک تابع دیگر بیان کرد. به ویژه تحلیلی است.
چندین قضیه پیلی-وینر در مورد رابطه بین خواص فروپاشی f و خواص تبدیل لاپلاس در ناحیه همگرایی وجود دارد.
در کاربردهای مهندسی، یک تابع مربوط به یک سیستم خطی زمان ناپذیر (LTI) پایدار است اگر هر ورودی محدود یک خروجی محدود تولید کند. این معادل همگرایی مطلق تبدیل لاپلاس تابع پاسخ ضربه در ناحیه Re(s) ≥ 0 است. در نتیجه، سیستمهای LTI پایدار هستند، مشروط بر اینکه قطبهای تبدیل لاپلاس تابع پاسخ ضربه دارای بخش واقعی منفی باشند.
این ROC برای آگاهی از علیت و پایداری یک سیستم استفاده می شو
منابع
[ویرایش]ویکی پدیای فارسی
معادله دیفرانسیل
در ریاضیات، معادله دیفرانسیل نوعی معادله ریاضی است که دارای یک (یا چند) تابع مجهول از یک یا چند متغیر مستقل و مشتقات آن توابع (با ترتیبات مختلف) است. از این معادلات در مدلسازی ریاضی بسیاری از پدیده های طبیعی استفاده می شود. بسیاری از قوانین عمومی طبیعت (در فیزیک، شیمی، زیست شناسی و نجوم) طبیعی ترین بیان ریاضی خود را در زبان معادلات دیفرانسیل می یابند. از جمله کاربردهای آن می توان به مدارهای الکتریکی، محدودیت سرعت،غلظت مواد شیمیایی و رشد جمعیت اشاره کرد. معادلات دیفرانسیل نیز کاربردهای زیادی در هندسه و مهندسی و بسیاری از زمینه های دیگر دارند. هر گاه میزان تغییر یک (یا چند) تابع با خود یا متغیرهای آن رابطه داشته باشد، آن پدیده با یک معادله دیفرانسیل مدل می شود. به عنوان مثال در مکانیک، حرکت جسم به وسیله سرعت و مکان آن در زمانهای مختلف توصیف میشود و معادلات نیوتن به ما رابطه بین مکان و سرعت و شتاب و چندین نوع وارد بر جسم را میدهند. در چنین شرایطی میتوانیم حرکت جسم را در قالب یک معادلهٔ دیفرانسیلی که در آن مکان ناشناختهٔ جسمی از زمان است بیان کنیم.
پیدا کردن جواب
[ویرایش]
برای بسیاری از معادلات دیفرانسیل، ممکن است جوابی وجود نداشته باشد یا جوابشان یکتا نباشد. در صورتی که جواب یکتا وجود داشته باشد نیز، در اکثر مواقع اثبات میشود که جواب به صورت یک تابع مقدّماتی قابل بیان نیست.
به عنوان مثال، جواب معادلهٔ دیفرانسیل را تابع انتگرال سینوس مینامیم . با وجود این که این تابع یک تابع مقدّماتی نیست، همهٔ خصوصیات این تابع با کامپیوتر قابل محاسبه اند (که در این مورد با توابع مثلّثاتی و نمایی تفاوتی ندارد).
در حقیقت، تابع نمایی نیز به این صورت تعریف میشود: تابعی که در معادلهٔ دیفرانسیل صدق کند را مینامیم (). در نتیجه ریاضیدانان جواب معادلات دیفرانسیل پرکاربرد را نامگذاری میکنند. به عنوان مثالی دیگر میتوان به توابع بسل اشاره کرد.
بنابرین، جواب اکثر معادلات دیفرانسیل خود یک تابع جدید است که با روشهای عددی (تقریبی) و کامپیوتری (مانند روشهای رونگه-کوتا) حل میشوند (از روشهای دیگر عددی میتوان به روش اویلر، روش هون، روش تیلور، آدامز-بشفورث-مولتون، روش میلن سیمپسون، روش هامینگ، روش رانگ-کوتا فلبرگ مرتبه ۵، روش رحمانزاده کای وایت، روشهای طیفی و شبه طیفی، روشهای شبکهای همانند اجزای محدود و تفاضل محدود و روشهای بدون شبکه اشاره کرد).
در صورتی که جواب یک معادله وجود داشته باشد و یکتا باشد و به صورت یک تابع مقدّماتی قابل بیان باشد، برای پیدا کردن آن از روشهای حل تحلیلی استفاده میشود (تنها برای سادهترین معادلات دیفرانسیل جواب صریح وجود دارد).
در این حالت نیز یک راه حل کلّی برای حل تمام معادلات دیفرانسیل (قابل حل تحلیلی) وجود ندارد. دلیل این موضوع میتواند این باشد که هنوز چنین راه حلّی کشف نشده باشد یا این که چنین راه حل کلّی وجود نداشته باشد. به همین دلیل این معادلات به چند دسته تقسیم میشوند که برای هر کدام راه حلّی کشف شدهاست.
بعضی از معادلات دیفرانسیل در هیچکدام از این دستهها نیز قرار نمیگیرند و راه حلّی (تحلیلی) برای آنها وجود ندارد. در این میان روشهای نیمهتحلیلی نیز وجود دارد که از آنها میتوان به روش تجزیه آدومیان، آنالیز هموتوپی، تبدیل دیفرانسیل اشاره کرد.
در نتیجه، برای حل یک معادلهٔ دیفرانسیل ابتدا باید بررسی کنیم که آیا جواب یکتا برای آن وجود دارد یا خیر و سپس این که در چه شاخهای قرار دارد. اگر برای شاخهٔ مورد نظر حل تحلیلی وجود داشت، از آن روش استفاده میکنیم و در غیر این صورت از روشهای عددی استفاده میکنیم. مسلّماً اگر جواب عددی برایمان کافی باشد، میتوانیم از همان ابتدا از روش عددی استفاده کنیم.
مقدار مسائل اولیه و حل مسائل کل
[ویرایش]در حل مسائل کلّی به ثابت انتگرال برمیخوریم. به عنوان مثال:
به این معنی که مقدار پادمشتق میتواند هر تابع (به ازای هر ) باشد. به عبارتی دیگر تابع ممکن است یا یا موارد مشابه باشد.
در صورتی که مقدار اوّلیّهٔ را بدانیم، میتوان آن را به صورت دقیق پیدا کرد. در مثال قبلی، اگر بدانیم از این موضوع نتیجه میگیریم:
به عنوان مثال، اگر بدانیم سرعت یک جسم () برابر ۱ است و همچنین در ثانیهٔ ۱ در مکان ۲ قرار داشته، از روش مذکور برای پیدا کردن معادلهٔ مکان-زمان استفاده میکنیم.
منابع
[ویرایش]ویکی پدیای فارسی
مثلثات
مثلثات شاخه ای از ریاضیات است که به بررسی روابط بین طول اضلاع و زوایای مثلث می پردازد. اولین کاربرد مثلثات در مطالعات نجوم بود. اکنون مثلثات در زمینه های ریاضیات محض و کاربردی، فیزیک و ... کاربردهای فراوانی دارد. برخی از روشهای اساسی تحلیل، مانند تبدیل فوریه و معادلات موج، از توابع مثلثاتی برای توصیف رفتار تناوبی موجود در بسیاری از فرآیندهای فیزیکی استفاده میکنند. همچنین، مثلثات اساس علم نقشه برداری است. ساده ترین کاربرد مثلثات در مثلث قائم الزاویه است. هر شکل هندسی دیگری نیز می تواند به مجموعه ای از مثلث های قائم الزاویه تبدیل شود. شکل خاصی از مثلثات مثلثات کروی است که برای مطالعه مثلثات روی سطوح کروی و منحنی استفاده می شود.
تاریخچه
[ویرایش]مثلثات ار دورانهای دور نیز استفاده میشده است و آن را در معماری، محاسبه مساحت و حجم، نجوم و... استفاده میکردند، مثلثات اولیه به دوران تمدن بابل، سومر، ایران و یونان باز میگردد، در لوح پلیمپتون۳۲۲ در مثلثات اولیه یعنی محاسبه وتر مثلث قائم الزاویه نام برده است
در دوران اسلامی مثلثات گسترش پیدا کرد
خواجه نصیرالدین طوسی اولین کسی بود که مثلثات را بعنوان شاخهای از ریاضیات معرفی کرد.
بتانی منجم مسلمان قرن دهم میلادی اولین کسی بود که فرمولهای مثلثاتی امروزی را ابداع کرد.
واژگان مثلثات در متون فارسی و عربی قدیم با امروزه تفاوت داشت:
| نام قدیم در فارسی | معنی نام | نام امروزی |
|---|---|---|
| جیب | گریبان | سینوس |
| جیب تمام | گریبان پُر | کسینوس |
| ظل، ظل معکوس | سایه | تانژانت |
| ظل تمام، ظل مستوی | سایه پُر | کتانژانت |
| قاطع، قطر ظل | بُرنده | سکانت |
| قاطع تمام | بُرنده پُر | کسکانت |
امروزه مثلثات کاربردهای زیادی در سری فوریه، تبدیل فوریه،انتگرال، مساحت و حجم، آنالیز، حسابان و... دارد.
کلیات
[ویرایش]تابعهای اصلی مثلثات
[ویرایش]
مجموع زاویههای داخلی مثلث برابر ۱۸۰ درجه است؛ بنابراین در مثلث قائمالزاویه با داشتن مقدار یک زاویه تند، میتوان مقدار زاویه دیگر را به دست آورد. با مشخص بودن زاویهها میتوان نسبت میان اضلاع را یافت. به این ترتیب، اگر اندازهی یک ضلع معلوم باشد، اندازه دو ضلع دیگر قابل محاسبه است. نسبت میان اضلاع مثلث، با استفاده از توابع مثلثاتی زیر، محاسبه میشود. در شکل روبرو، برای زاویه تند A که مجاور وتر c و ضلع b و روبرو به ضلع a است، داریم:
- تابع سینوس که به صورت نسبت ضلع مقابل به وتر تعریف میشود:
- تابع کسینوس که به صورت نسبت ضلع مجاور به وتر تعریف میشود:
- تابع تانژانت که به صورت نسبت ضلع مقابل به ضلع مجاور تعریف میشود:
توابع مثلثاتی برای زاویه B نیز به همین ترتیب قابل محاسبه هستند. از آنجایی که ضلع مقابل زاویه A مجاور زاویه B است و برعکس، سینوس یک زاویه برابر با کسینوس زاویهی دیگر است. به عبارت دیگر: و .
عکس تابعهای بالا نیز با نامهای سکانت (معکوس کسینوس)، کسکانت (معکوس سینوس) و کتانژانت (معکوس تانژانت) تعریف میشوند.
| سکانت: | |
| کسکانت: | |
| کتانژانت: |
دایره واحد مثلثاتی
[ویرایش]
تابعهای مثلثاتی برای زاویههای تند بر اساس رابطههای بالا محاسبه میشوند. برای زاویههای بزرگتر از ۹۰ درجه (π/۲ رادیان)، میتوان از مفهوم دایره مثلثاتی بهره گرفت. در دایره مثلثاتی، هر زاویهای از صفر تا ۳۶۰ درجه را میتوان رسم کرد و تابعهای مثلثاتی آن را به دست آورد. همان گونه که در شکل روبرو دیده میشود، تابعهای مثلثاتی برای زاویههای بزرگتر از ۹۰ درجه را میتوان به صورت تابعی از زاویههای کوچکتر از ۹۰ درجه، یافت. برای نمونه، تابعهای مثلثاتی برای زاویههای ربع دوم دایره (۹۰ تا ۱۸۰ درجه) با دوران دایره مثلثاتی به میزان ۹۰ درجه، به صورت جدول زیر به دست میآیند:
| دوران π/۲ |
|---|
تناوب
[ویرایش]تابعهای مثلثاتی برای زاویههای بزرگتر از ۳۶۰ درجه (۲π) و کوچکتر از صفر درجه نیز تعریف میشوند. برای هر زاویه 'θ مقدار تابع، برابر با مقدار تابع برای زاویه θ درون دایره (۰<θ<۳۶۰) خواهد بود که در رابطه θ'=۳۶۰+۲kθ صدق کند؛ بنابراین تابعهای مثلثاتی با یک تناوب مشخص تکرار میشوند. دوره تناوب تابعهای تانژانت و کتانژانت، ۱۸۰ درجه (π) و دوره تناوب سایر تابعها ۳۶۰ درجه (۲π) است.
تابع وارون
[ویرایش]برای تابعهای مثلثاتی، تابع وارون در بازه مشخصی که شرط یک به یک بودن تابع برقرار باشد، تعریف میشود. این تابعها متناظر با تابع اصلی، آرکسینوس، آرککسینوس و آرکتانژانت نامیده میشوند.
زاویههای مرزی
[ویرایش]| ربع | زاویه + | زاویه - |
|---|---|---|
| ربع اول | ||
| ربع دوم | ||
| ربع سوم | ||
| ربع چهارم |
جدول مثلثات در دایره به صورت زاویه
[ویرایش]| نسبتهای مثلثاتی | ربع اول | ربع دوم | ربع سوم | ربع چهارم |
|---|---|---|---|---|
مثلثات در مساحت و حجم
[ویرایش]کاربرد مثلثات در مساحت و حجم منشور های چندپهلو،چندوجهی منتظم یکنواخت،چندضلعی ها استفاده می گردد.
| اشکال هندسی | مساحت | حجم |
|---|---|---|
| منشور چندپهلو | ||
| چندوجهی منتظم یکنواخت | نامعلوم | |
| چندضلعی منتظم | سه بعدی نیست |
حجم چندوجهی بر اساس ترکیب حجم کره،شعاع چندوجهی و مساحت چندضلعی منتظم بدست می آید.
چندضلعی منتظم یک جسم دوبعدی است و حجمی ندارد.
منابع
[ویرایش]چندضلعی منتظم
ویکی پدیای فارسی
مساحت و حجم
منشور
مثلثات کروی
مثلثات کروی علمی است که به بررسی روابط بین زاویهها و اضلاع یک مثلث کروی (در هندسه نااقلیدسی) میپردازد. مثلثات کروی شاخهای از هندسه کروی است که با توجه به روابط بین توابع مثلثاتی دو طرف و زوایای چند ضلعی کروی (به ویژه مثلث کروی)؛ محدود شده توسط تعدادی از دایرههای بزرگ، در کره را بررسی میکند. کاربرد عملی مثلثات کروی در محاسبهها و براوردها در نجوم رصدی، زمینشناسی و ناوبری، و نیز قبله یابی، بسیار مهم است.
ویژگی ها
[ویرایش]
در این مثلثها مجموع زوایای داخلی بیشتر از ۱۸۰ درجه و حداکثر ۵۴۰ درجه میباشد.
قوانین معمول مثلثات تخت در این مثلثات صادق نیستند.
تمام اضلاع این مثلثات باید جزو دوایر عظیمه باشند.
قوانین
[ویرایش]قانون کسینوسها
[ویرایش]قانون سینوسها
[ویرایش]فرمول چهار جزئی
[ویرایش]چندضلعی های کروی
[ویرایش]چند ضلعی کروی چند ضلعی روی سطح کره است که توسط تعدادی کمان دایره بزرگ تعریف شده است که محل تلاقی سطح با صفحاتی است که از مرکز کره می گذرد. چنین چند ضلعی ممکن است هر تعداد ضلع داشته باشد. دو صفحه یک لون را تعریف می کنند که به آن " دیگون " یا دو زاویه نیز می گویند، آنالوگ دو طرفه مثلث: یک مثال آشنا، سطح منحنی قسمتی از یک پرتقال است. سه صفحه یک مثلث کروی را تعریف می کنند که موضوع اصلی این مقاله است. چهار صفحه یک چهارضلعی کروی را تعریف می کنند: چنین شکلی و چندضلعی های ضلعی بالاتر همیشه می توانند به عنوان تعدادی مثلث کروی در نظر گرفته شوند.
از این نقطه مقاله به مثلثهای کروی محدود میشود که به سادگی به عنوان مثلث نشان داده میشوند
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
تابع(ریاضیات)
تابِع یا پَردازه به پارسی، در ریاضیات یک رابطه دوتایی روی دو مجموعه است که هر عنصر در مجموعه اول را دقیقاً به یک عنصر در مجموعه دوم مرتبط میکند. مثالهای معمول در این زمینه، توابعی از اعداد صحیح به اعداد صحیح یا از اعداد حقیقی به اعداد حقیقی است.
در اصل توابع ایدهآلسازی این که چگونه یک متغیر بر متغیری دیگر وابسته است بودند. برای نمونه، موقعیت یک سیاره تابعی از زمان است. از لحاظ تاریخی، در پایان سده هفده میلادی این مفهوم توسط حسابان توضیح داده میشد و تا سده نوزدهم توابعی که در نظر گرفته میشدند دیفرانسیلپذیر بودند. مفهوم یک تابع در پایان سده ۱۹ از دیدگاه نظریه مجموعهها رسمی شد و این امر دامنه کاربرد این مفهوم را تا حد زیادی افزایش داد.
تابع یک پروسه یا رابطهای است که دستهای از یک x در دامنه X را به یک y در دامنه Yها متصل میکند، که به آن همدامنه تابع میگویند. معمولا آن را با حرفهایی مانند f، g یا h نشان میدهند.
اگر تابعمان f خوانده میشود، رابطه آن به شکل(y=f (x نشان داده میشود. در این رابطه، x شناسه تابع یا ورودی تابع است و y «خروجی» تابع است. نمادی که برای نشان دادن ورودی استفاده میشود یک متغیر از تابع است، برای نمونه f متغیر x است.
از توابع بهطور گستردهای در گونههای مختلف علم و بیشتر در ریاضیات استفاده میشود. گفته شدهاست که توابع «موضوعات اصلی تحقیق» در بیشتر رشتههای ریاضیات است.
منابع
[ویرایش]ویکی پدیای فارسی
در حال تحقیق...
لگاریتم
لُگاریتم (به انگلیسی: Logarithm) یک عدد در یک پایه، برابر با توانی از پایهاست که آن عدد را میدهد. برای نمونه لگاریتم ۱۰۰۰ در پایهٔ ۱۰، برابر با ۳ است. چون ۱۰ × ۱۰ × ۱۰ = ۱۰۰۰ یا به بیان کلیتر اگر x = by باشد آنگاه لگاریتم x در پایهٔ b برابر با y خواهد بود و به زبان ریاضی آن را به صورت نمایش میدهیم. مانند:
لگاریتم نخستین بار از سوی جان نپر در اوایل سده ۱۷ میلادی به عنوان وسیلهای برای آسانتر کردن محاسبات، معرفی شد؛ که به سرعت از سوی دانشمندان و مهندسان پذیرفته شد و برای آسانتر کردن و سریعتر کردن محاسبه جدولهای لگاریتم اعشاری و خطکشهای لغزنده ایجاد شدند و مورد استفاده قرار گرفتند. تمامی این ابزارها بر پایهٔ این مفهوم که «لگاریتم حاصل ضرب برابر است با مجموع لگاریتمها»، ساخته شده بودند:
مفهوم امروزی لگاریتم از تلاشهای لئونارد اویلر در قرن ۱۸ گرفته شدهاست؛ او توانست مفهوم لگاریتم را با مفهوم تابع نمایی پیوند دهد.
لگاریتم در پایهٔ ۱۰ را لگاریتم اعشاری مینامند که کاربرد بسیار زیادی در مهندسی دارد. لگاریتم در مبنای ثابت e یا عدد نپر ≈ ۲٫۷۱۸ را لگاریتم طبیعی مینامند. این لگاریتم در ریاضیات محض به ویژه حساب دیفرانسیل و انتگرال بسیار کاربرد دارد. لگاریتم دو دویی نیز در مبنای ۲ نوشته میشود و کاربرد زیادی در علوم رایانه دارد.
به کمک مقیاس لگاریتمی، میتوان اندازههای بسیار بزرگ را در ابعاد بسیار کوچکتری نشان داد برای نمونه دسیبل یکایی لگاریتمی است که برای نشان دادن فشار صدا و نسبت ولتاژ کاربرد دارد. در شیمی نیز پ هاش که معیاری برای نشان دادن میزان اسیدی بودن مایعات است در مقیاس لگاریتمی بیان میشود. همچنین لگاریتم در نظریهٔ پیچیدگی محاسباتی و در برخی شکلهای هندسی مانند برخالها کاربرد دارد. از دیگر کاربردهای آن میتوان به فاصله در موسیقی و رابطههای شمارش اعداد اول اشاره کردهمچنین در محاسبه زمان اجرای الگوریتمهای برنامههای کامپیوتری استفاده میشود.
تابع توان وارون تابع لگاریتم است و لگاریتم مختلط، تابع وارون تابع نمایی به کار رفته در اعداد مختلط است. لگاریتم گسسته نیز در رمزنگاری کلید عمومی استفاده میشود.
انگیزهٔ اولیه و تعریف
[ویرایش]انگیزهٔ ساخت لگاریتم، داشتن وارون تابع توان بودهاست. برای نمونه، توان سوم ۲، ۸ است چون ۸ = ۲ × ۲ × ۲ = ۲۳ پس لگاریتم ۸ در پایهٔ ۲، ۳ میشود.
به توان رساندن
[ویرایش]توان سوم عددی مانند b برابر است با ۳ بار ضرب b در خودش. حال اگر b به توان یک عدد طبیعی مانند n برسد به معنی n بار ضرب کردن b در خودش است که به صورت زیر نمایش میدهیم
در صورتی که n عدد طبیعی نباشد، آنگاه bn جواب دیگری خواهد داشت. مانند ۱- که b-۱ برابر معکوس b است. برای جزئیات بیشتر، شامل فرمول bm + n = bm · bn توان را ببینید یا یک رساله مقدماتی.
تعریف
[ویرایش]لگاریتم عددی مانند y در پایهٔ b عبارت است از یافتن عددی که اگر b به توان آن عدد برسد برابر با y شود. به عبارت دیگر جواب x معادلهٔ زیر برابر با لگاریتم y در پایهٔ b خواهد بود.
پایهٔ b باید یک عدد حقیقی مثبت و نامساوی ۱ باشد و y نیز باید یک عدد مثبت باشد.
چند نمونه
[ویرایش]- نمونهٔ یکم
برای نمونه ۴ = (۱۶) log۲ چون ۱۶ = ۲ × ۲ × ۲ × ۲ = ۲۴
- نمونهٔ دوم
برای توانهای منفی نیز لگاریتم معتبر است مانند:
چون
- نمونهٔ سوم
(۱۵۰) log۱۰ تقریباً برابر است با ۲٫۱۷۶ عددی میان ۲ و ۳ چون ۱۵۰ خود عددی است میان ۱۰۰ = ۱۰۲ و ۱۰۰۰ = ۱۰۳ همچنین در هر پایهای و چون به ترتیب: و است.
ویژگیهای ریاضی
[ویرایش]مطالعهٔ بیشتر در بحث لگاریتم نیازمند مطرح کردن مفهوم تابع است. یک تابع مانند یک قانون عمل میکند که اگر یک عدد ورودی داشته باشد، در مقابل یک خروجی تولید میکند. مانند تابع توان x ام عدد حقیقی b که به صورت زیر نوشته میشود:
تابع لگاریتم
[ویرایش]برای درک تابع لگاریتم باید نشان داد که معادلهٔ زیر:
دارای راه حل و جواب یکتای x است به شرطی که y بزرگتر از صفر باشد و b بزرگتر از صفر و نامساوی ۱ باشد. برای اثبات این مطلب باید از قضیهٔ مقدار میانی در حساب دیفرانسیل و انتگرال استفاده کرد. این قضیه نشان میدهد که اگر تابع پیوستهای دو مقدار m و n را تولید کند، هر مقداری میان این دو عدد را نیز به دلیل پیوستگی میتواند تولید کند. یک تابع را زمانی پیوسته میدانیم که در هیچ نقطهای ار آن «پرش» نداشته باشیم و بدون بلندکردن قلم از روی کاغذ بتوانیم خم آن را بکشیم. میتوان نشان داد که در تابع نیز همین ویژگی وجود دارد، برای هر y> ۰ که میان دو مقدار و به ازای x۰ و x۱ قرار داشته باشد طبق قضیهٔ مقدار میانی میتوان یک x پیدا کرد که باشد؛ بنابراین برای معادلهٔ یک جواب پیدا شد که میتوان گفت تنها جواب این معادلهاست چون تابع f برای b> ۱ اکیداً صعودی و برای b میان ۰ و ۱ اکیداً نزولی است.
جواب پیدا شده برای این معادله همان لگاریتم y در پایهٔ b است.
قرینه تابع لگاریتمی
[ویرایش]اگر قرینه تابع برابر با باشد نسبت به محور yها قرینه هم هستند.
اگر قرینه تابع برابر با باشد نسبت به محور xها قرینه هم هستند.
تابع وارون
[ویرایش]
لگاریتم تابع توانی برای هر عدد x به صورت زیر نوشته میشود:
اگر پایهٔ توان و لگاریتم هر دو b باشد جواب نهایی رابطهٔ بالا قطعاً خود x خواهد بود. همچنین اگر عدد مثبت y را داشته باشیم، رابطهٔ زیر نیز برقرار خواهد بود:
بنابراین در هر دو صورت میتوان دو تابع توانی و لگاریتم را ترکیب کرد و دوباره به مقدار اولیه رسید. پس لگاریتم در پایهٔ b تابع وارون f(x) = bx است.
دو تابع وارون همواره با یکدیگر ارتباط دارند به این ترتیب که خمهای آنها قرینهٔ یکدیگر نسبت به خط y = x است (مانند شکل) همچنین در تابع اگر x به سمت مثبت بینهایت برود مقدار تابع لگاریتم نیز به ازای b> ۱ به سمت مثبت بینهایت خواهد رفت در این حال میگوییم تابع اکیداً صعودی است. به ازای b <۱ اگر x به سمت مثبت بینهایت رود، مقدار تابع به سمت منفی بینهایت میرود. وقتی x به سمت صفر میرود مقدار تابع برای b> ۱ به سمت منفی بینهایت میرود و برای b <۱ به سمت مثبت بینهایت میرود.
مشتق و پادمشتق
[ویرایش]
ویژگیهای ریاضی یک تابع را میتوان در تابع وارون آن نیز جستجو کرد. پس چون یک تابع پیوسته و مشتقپذیر است، میتوان نتیجه گرفتکه نیز همین ویژگی را دارد. یک تابع پیوسته مشتقپذیر است اگر هیچ نقطهٔ تیزی (نقطهٔ شکستگی) در آن وجود نداشته باشد. از آنجایی که میتوان نشان داد که مشتق برابر با است، با استفاده از ویژگیهای تابع نمایی و قاعدهٔ زنجیری به این نتیجه میرسیم که مشتق برابر است با:
که این شیب خط مماس در نقطهٔ x بر خم است که برابر است با . همچنین مشتق برابر با است که به این معنی است که پادمشتق همان است. اگر به جای x حالت کلی را در نظر بگیریم، در این حالت خواهیم داشت:
گاهی برای بدست آوردن مشتق تابع f از استفاده میکنند که به این کار مشتقگیری لگاریتمی میگویند. پادمشتق لگاریتم طبیعی برابر است با:
رابطههای مرتبط با دیگر پایههای لگاریتم با استفاده از فرمول لگاریتم طبیعی که در بالا گفته شد بدست میآید.
بیان انتگرالی لگاریتم طبیعی
[ویرایش]لگاریتم طبیعی t برابر است با انتگرال از ۱ تا t:
به عبارت دیگر برابر است با سطح میان محور xها و نمودار تابع از ۱ = x تا (شکل مقابل). این مطلب، از نتایج قضیهٔ اساسی حسابان و اینکه مشتق ، است، میباشد. عبارت سمت راست این رابطه را میتوان به عنوان تعریفی برای لگاریتم طبیعی در نظر گرفت. فرمولهای ضرب و توان لگاریتمی را میتوان از این تعریف نتیجه گرفت. برای نمونه را میتوان به صورت زیر نتیجه گرفت:
بخش نخست تساوی انتگرال را به دو بخش جدا میشکند و بخش دوم تساوی، تغییر متغیر میدهد (). در نگارهای که در پایین نشان داده شدهاست، سطح زیر منحنی که برابر با انتگرال بالا است به دو ناحیهٔ آبی و زرد تقسیم شدهاست. در قسمت آبی همانطور که خم در جهت x کشیده شده (t برابر شده) به همان اندازه هم در جهت عمودی دچار جمع شدگی شدهاست بنابراین سطح زیر منحنی سمت راست که انتگرال f(x) = ۱/x از ۱ تا u است با سطح زیر آن از t تا tu برابر است. پس روی شکل سمت چپ نشان داده شد که یا سطح زیر منحنی برابر است با مجموع و (سطح زرد و آبی)

رابطهٔ توان را نیز به همین ترتیب میتوان اثبات کرد:
در تساوی دوم تغییر متغیر را داریم.
مجموع وارونهای اعداد طبیعی:
که سری هارمونی نام دارد، به لگاریتم طبیعی بسیار نزدیک است: هرگاه n به سمت بینهایت برود، تفاضل زیر:
به عددی معروف به ثابت اویلر-مسکرونی، همگرا میشود. این ارتباط در تحلیل عملکرد الگوریتمهایی مانند مرتبسازی سریع کمک میکند.
حالت کلی
[ویرایش]
عدد مختلط a جواب معادلهٔ زیر، یک لگاریتم مختلط است.
z عددی مختلط است. یک عدد مختلط را به صورت z = x + iy نمایش میدهیم که x و y هر دو عددی حقیقی و i یکهٔ موهومی است. چنین عددی را میتوان با یک نقطه بر روی صفحهٔ مختلط نمایش داد (مانند روبرو). فرم قطبی نمایش دهندهٔ عدد ناصفر مختلط z است که قدر مطلق آن برابر است با فاصلهٔ r تا مبدأ مختصات و زاویهٔ میان خط گذرا از z و مبدأ با محور x زاویهٔ مربوط به این عدد مختلط است. قدر مطلق z همان r است که برابر است با:
چون φ' = φ + ۲π پس هم φ و هم 'φ هر دو زاویهٔ مربوط به zاند. تنها یک φ است که در رابطهٔ −π <φ صدق میکند که به آن آرگومان اصلی گفته میشود و به صورت نمایش داده میشود. گاهی هم به صورت ۰ ≤ Arg(z) <2π تعریف میشود.
با بهرهگیری از تابعهای مثلثاتی سینوس و کسینوس یا شکل نمایی اعداد مختلط به ترتیب به رابطههای زیر میرسیم، r و φ را بالاتر تعریف کردیم:
در آغاز معادلهای را بیان کردیم که در آن توان a ام e برابر با z میشد. با توجه به آنچه گفته شد، مقدار a برابر خواهد بود با:
در این رابطه، n هر عدد صحیحی میتواند باشد.
منابع
[ویرایش]ویکی پدیای فارسی
تابع لگاریتمی
تابع لگاریتمی،تابعی است که در آن مجموعه های لگاریتمی در نمودار تابعی به نمایش می گذارد.در تابع لگاریتمی،تمام ریشه های اعداد را محاسبه می کنیم و در تابع لگاریتمی نشان می دهیم.این نوع تابع برای لگارتیم بسیار کاربردی است.
تعریف
[ویرایش]توابع لگاریتمی معکوس توابع نمایی هستند و هر تابع نمایی را می توان به صورت لگاریتمی بیان کرد. به طور مشابه، تمام توابع لگاریتمی را می توان به صورت نمایی بازنویسی کرد. لگاریتم ها واقعاً مفید هستند و به ما اجازه می دهند با اعداد بسیار بزرگ کار کنیم و در عین حال اعدادی با اندازه بسیار قابل کنترل تر را دستکاری کنیم.
قانون کل
[ویرایش]در تابع لگاریتمی اگر تابع ما برحسبfباشد وxعدد ریشه یابی باشد وaعدد لگارتیم بایشد وyریشه آن عدد باشد به صورت زیر می نویسیم.
مثال:
[ویرایش]در تابع لگاریتمیx=250،لگارتیم آن را پیدا کنید به شربط آنکه ریشه لگاریتمی برابر با10 باشد
[ویرایش]حل:
[ویرایش]ابتدا رابطه را می نویسیمو در اینجا عددyعدد مجهول است.
بعد چون ۲۵۰ بین عدد۱۰۰و۱۰۰۰است پس باید ریشه آن بین عدد۲و۳باشد و به عدد۱۰۰نزدیک تر است. پس جواب برابر با این رابطه است:
اثبات:
[ویرایش]
فرم تابع
[ویرایش]فرم تابع لگاریتمی به همراه حل به این شکل است
منابع
[ویرایش]
تابع نمایی
تابع نمایی (به انگلیسی: Exponential function) تابعی مهم در ریاضیات است و معمولاً بهصورت یا نوشته میشود که عدد اویلر(ثابت نپر) با مقدارِ تقریبی ۲٫۷۱۸۲۸۱۸۲۸ است.
البته، این تابع را میتوان به صورت نیز تعریف کرد. استفاده از لگاریتم نشان میدهد که:
این تابع را تابع نمایی با پایهٔ میخوانیم که عددی ثابت است.
در بسیاری از علوم وقتی از تابع نمایی صحبت میشود، منظور تابع است.
عموماً متغیر میتواند هر عدد حقیقی یا مختلط باشد. به عبارت دیگر، معکوس را گویند.
تعریف رسمی
[ویرایش]
تابع نمایی واقعی را میتوان به روشهای مختلف معادل مشخص کرد. معمولاً با سریهای قدرت زیر تعریف میشود: از آنجایی که شعاع همگرایی این سری توانی نامحدود است، این تعریف در واقع برای همه اعداد مختلط قابل استفاده است (به بخش مختلط برای گسترش به صفحه مختلط). سپس ثابت е را می توان به صورت زیر تعریف کرد.
تمایز ترم به ترم این سری توان نشان می دهد که
برای همه x واقعی ، منجر به یکی دیگر از خصوصیات رایج به عنوان راه حل منحصر به فرد معادله دیفرانسیل می شود. ارضای شرط اولیه بر اساس این مشخصه، قاعده زنجیره نشان می دهد که تابع معکوس آن، لگاریتم طبیعی، را بروارده می کند.برای یا
این رابطه منجر به تعریف کمتری از تابع نمایی واقعی به عنوان راه حل معادله می شود. با استفاده از قضیه دو جمله ای و تعریف سری توان، تابع نمایی نیز می تواند به عنوان حد زیر تعریف شود:
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
معادله خطی
معادلهٔ خطی (به انگلیسی: Linear equation) یک معادلهٔ جبری است که در آن هر جمله، یا متغیر است یا حاصلضرب یک ثابت و تنها یک متغیر با توان یک. این معادلات ممکن است یک یا چند متغیر داشته باشند. این معادلات دارای یک ریشه بوده و در صورتی که همهٔ اعداد و ضرایب معادله حقیقی باشند آنگاه جواب نیز در مجموعه اعداد حقیقی تعیین خواهد شد. شکل عموم این نوع معادلات بدین صورت است: که در آن و اعداد ثابتی میباشند ( مخالف صفر) و هم مجهول میباشد. پاسخ چنین معادله ای برابر است با منفی تقسیم بر .

قضیه
[ویرایش]معادله خط اینگونه است y=ax+b
تعریف
[ویرایش]به طور متناوب، یک معادله خطی را می توان با معادل صفر کردن یک چند جمله ای خطی در یک میدان ، که ضرایب از آن گرفته می شود، به دست آورد.
راه حل های چنین معادله ای مقادیری هستند که با جایگزینی مجهولات، برابری را درست می کنند.
در مورد فقط یک متغیر، دقیقا یک راه حل وجود دارد (به شرط آن). اغلب، اصطلاح معادله خطی به طور ضمنی به این مورد خاص اشاره دارد، که در آن متغیر به طور معقولی مجهول نامیده می شود .
در مورد دو متغیر، هر راه حل ممکن است به عنوان مختصات دکارتی یک نقطه از صفحه اقلیدسی تفسیر شود . راه حل های یک معادله خطی یک خط را در صفحه اقلیدسی تشکیل می دهند و برعکس، هر خط را می توان به عنوان مجموعه ای از تمام راه حل های یک معادله خطی در دو متغیر مشاهده کرد. این منشأ اصطلاح خطی برای توصیف این نوع معادلات است. به طور کلیتر، راهحلهای یک معادله خطی در n متغیر یک ابر صفحه (فضای فرعی با بعد n - 1 ) را در فضای اقلیدسی بعد n تشکیل میدهند .
معادلات خطی اغلب در تمام ریاضیات و کاربردهای آنها در فیزیک و مهندسی اتفاق میافتد ، تا حدی به این دلیل که سیستمهای غیرخطی اغلب به خوبی با معادلات خطی تقریب میشوند.
این مقاله به بررسی یک معادله منفرد با ضرایب از میدان اعداد حقیقی می پردازد که پاسخ های واقعی برای آن مطالعه می شود. تمام محتوای آن برای حل های پیچیده و به طور کلی برای معادلات خطی با ضرایب و راه حل ها در هر زمینه اعمال می شود . برای چند معادله خطی همزمان، به سیستم معادلات خطی مراجعه کنید .
متغیرها
[ویرایش]یک متغیر
[ویرایش]یک معادله خطی در یک متغیر به شکل است که در آن وواقعی هستند. اعداد و . ریشه .
دو متغیر
[ویرایش]یک معادله خطی در دو متغیرو به شکل است که در آن ، و اعداد حقیقی هستند به طوری که . بی نهایت راه حل های ممکن دارد
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
جبر و معادله
جبر و معادله،دو واژه عربی هستند که به معنای جبران و تعادل هستند.جبر در ریاضی به مبنای یک عدد انگلیسی یا یونانی یا لاتین به جای اعداد اصلی باشد.معادله به معنای یک ترازه برای دو عبارت که اگر چیزی از عبارت کم شد از عبارت دیگر هم کم شود،یا برعکس اگر بیشتر شد،باید از عبارت دیگر بیشتر شود

جبر
[ویرایش]کلمه جبر از عربی آمده است:(الجبر)«به معنای اتصال مجدد قطعات شکسته،استخوان بندی» از عنوان کتاب اوایل قرن نهم کتاب علم الجبر و المقابله «علم ترمیم و تعادل» توسط ریاضیدان و ستاره شناس ایرانی الخوارزمی. اصطلاح الجبر در اثر او به عملیات جابجایی یک عبارت از یک طرف معادله به سمت دیگر اشاره دارد، المقابلة المقابله «تعادل» به افزودن عبارت مساوی به هر دو طرف اشاره دارد. این کلمه که در لاتین فقط به جبر یا جبر خلاصه شده است، در نهایت در قرن پانزدهم از اسپانیایی، ایتالیایی یا لاتین قرون وسطایی وارد زبان انگلیسی شد. در ابتدا به روش جراحی برای ایجاد استخوان های شکسته یا دررفته اشاره داشت. معنای ریاضی اولین بار (به زبان انگلیسی) در قرن شانزدهم ثبت شد.
معادله
[ویرایش]معادله در کتاب خوارزمی از واژه مقابله آمده که به معنای تعادل است.خوارزمی برای تعادل عبارات،الگوریتمی تنظیم کرد که اسم آن مقابله بود که الان به اسم معادله مشهور است.
معادله دو نوع است معادله خطی وغیر خطی.البته معادله حجمی هم وجود دارد.معادلاتی که مجهول آنها یک میباشد، معادله خطی ومعادلاتی که مجهول آنها دارای توان بیشتر از یک میباشد معادله غیر خطی میگویند.و معادلاتی که بیش از توان بیشتر دارد،معادله حجمی گویند. در ریاضی معادله معمولاً بیان برابری دو عبارت است که در یکی یا هردوی آنها متغیر یا متغیرهائی وجود دارند.
معادلههائی که فارغ از ارزش (یا مقدار) متغیرها همواره درست باشند، اتحاد نامیده میشوند. مثلاً معادله
اتحاد است چون هر چه باشد این برابری همواره درست است؛ ولی معادل
اتحاد نیست چون فقط اگر مقدار عدد ۱ باشد این برابری برقرار است. مقادیری از متغیرها را که باعث برقراری رابطه برابری در معادله میشود، «جواب معادله» مینامند. مثلاً در مثال قبل عدد ۱ جواب معادله است. پیدا کردن جواب معادله را «حل معادله» مینامند.
جَبر به همراه نظریه اعداد، هندسه و آنالیز، یکی از وسیعترین شاخههای ریاضیات است. جبر در عمومیترین حالت خود به مطالعه این نمادهای ریاضیاتی می پردازد؛ و ریسمانیست که تقریباً تمام ریاضیات را با هم یکپارچه می کند. این شاخه شامل مباحث زیادی مثل حل معادلات مقدماتی تا مطالعه تجریدهایی چون گروهها، حلقهها و میدانها است. بخش های مقدماتی تر جبر را جبر مقدماتی می نامند؛ و بخش های مدرن آن را جبر مجرد یا جبر مدرن می خوانند. جبر مقدماتی اغلب بخش مهم مطالعه ریاضیات، علوم یا مهندسی به علاوه علوم کاربردی دیگری چون پزشکی و اقتصاد می باشد. جبر مجرد یکی از شاخه های اصلی ریاضیات پیشرفته است که عمدتاً توسط ریاضیدانان حرفه ای مطالعه می شود.

منابع
[ویرایش]
حد و پیوستگی تابع
حد و پیوستگی،دو روش مهم در علم حسابان است که بررسی و بی نهایتی توابع را با دنباله ها بررسی می کند،این دو روش برای محاسبه انتگرال کاربرد دارد.
تعریف حد
[ویرایش]بهطور کلی مفهوم حد در ریاضیات به این صورت است که اگر ورودیهای تابع رو به یک عدد نزدیک کنیم خروجیهای تابع به کدام عدد نزدیک میشوند. به عبارت دیگر، در حد، مقادیری از تابع سنجیده میشوند که برای دامنه آن مقدار مطلق و قابل شناسایی وجود ندارد، و اعدادی بسیار نزدیک به یک عدد خاص (که آن عدد خاص میتواند جزء دامنه تابع نباشد) یا اعدادی بسیار بزرگ (بینهایت) مقدار سنجی میشوند. فرض کنید در تابع f مقدار متغیر به یک عدد ثابت به نام a میل کند (یعنی به آن نزدیک شود ولی به آن نرسد) آنگاه اگر مقدار تابع آن، به عددی ثابت به نام L میل کند، L حد تابع f در نقطهٔ a خواهد بود؛ گرچه a میتواند در دامنهٔ تابع وجود نداشته باشد. به عبارت خیلی سادهتر میتوان گفت حد یک تابع برای یک عدد معین روی محور xها، به ما نشان میدهد که در صورت قرار دادن مجموعه اعدادی که در همسایگی خیلی خیلی نزدیک آن عدد معین هستند در xهای ضابطه تابع، yها به چه عددی خیلی خیلی نزدیک میشوند (تابع در نهایت به چه عددی خواهد رسید).
کاربرد مفهوم حد در ریاضی در توصیف مقداری است که یک تابع یا دنباله به آن نزدیک میشود، هنگامی که ورودی آن تابع یا شمارندهٔ آن دنباله به مقداری مشخص نزدیک میشود. حد یک مفهوم اساسی در حساب دیفرانسیل و انتگرال و در حالت کلی در آنالیز ریاضی است و در تعریف پیوستگی، مشتق و انتگرال کاربرد دارد. موضوع حد، به منظور بیان رفتار یک تابع میپردازد و میتواند رفتار آن را در نقاط روی صفحه یا در بینهایت هم ارزیابی کند.
مفهوم حد یک دنباله به حالت کلی تر حد شبکهٔ مکانشناسی گسترش مییابد و ارتباط نزدیکی با حد و حد مستقیم در نظریهٔ ردهها دارد.
ریاضیدانان پیش از آنکه مفهوم دقیقتر حد را ارائه کنند، در مورد آن مجادلههای بسیار کردهاند. یونانیها در عصر باستان درکی از مفهوم حد داشتهاند. برای نمونه ارشمیدس مقدار تقریبی را با استفاده از پیرامون چند ضلعیهای منتظم محاط در دایره به شعاع یک، وقتی که تعداد اضلاع بدون کران افزایش مییابد به دست میآورد. در قرون وسطی نیز تا دورهٔ رنسانس مفهوم حد برای بدست آوردن مساحت شکلهای گوناگون بکار گرفته میشد.
در نوشتار ریاضی حد را گاهی به صورت lim نمایش میدهند مانند lim(an) = a، گاهی با یک پیکان رو به راست (→) نمایش میدهند مانند: an → a و گاهی هم به فارسی حد مینویسند.
تعریف پیوستگی
[ویرایش]در ریاضیات، تابع پیوسته تابعی است به طوری که یک تغییر پیوسته (یعنی تغییر بدون جهش) آرگومان، تغییر پیوسته مقدار تابع را القا می کند. این بدان معنی است که هیچ تغییر ناگهانی در ارزش وجود ندارد که به عنوان ناپیوستگی شناخته می شود. به طور دقیق تر، یک تابع پیوسته است در صورتی که بتوان تغییرات دلخواه کوچک در مقدار آن را با محدود کردن به تغییرات به اندازه کافی کوچک آرگومان آن تضمین کرد. تابع ناپیوسته تابعی است که پیوسته نباشد. تا قرن 19، ریاضیدانان عمدتاً بر مفاهیم شهودی تداوم تکیه می کردند و فقط توابع پیوسته را در نظر می گرفتند. تعریف اپسیلون-دلتا از یک حد برای رسمی کردن تعریف تداوم معرفی شد.
پیوستگی یکی از مفاهیم اصلی حساب دیفرانسیل و انتگرال و تحلیل ریاضی است که در آن آرگومان ها و مقادیر توابع اعداد واقعی و مختلط هستند. این مفهوم به توابع بین فضاهای متریک و بین فضاهای توپولوژیکی تعمیم داده شده است. دومی کلی ترین توابع پیوسته هستند و تعریف آنها اساس توپولوژی است. یک شکل قویتر از تداوم، تداوم یکنواخت است. در نظریه نظم، به ویژه در نظریه حوزه، مفهوم مرتبط با پیوستگی، تداوم اسکات است.
به عنوان مثال، تابع (H(t که نشان دهنده ارتفاع یک گل در حال رشد در زمان t است پیوسته در نظر گرفته می شود. در مقابل، تابع (M(t که مقدار پول موجود در یک حساب بانکی را در زمان t نشان میدهد، ناپیوسته در نظر گرفته میشود، زیرا در هر نقطه از زمان که پول واریز یا برداشت میشود، "پرش" میکند.
منابع
[ویرایش]https://en.m.wikipedia.org/wiki/Continuous_function
https://fa.m.wikipedia.org/wiki/%D8%AD%D8%AF_(%D8%B1%DB%8C%D8%A7%D8%B6%DB%8C)
در حال تحقیق...
مشتق

مشتق (به انگلیسی Derivative) ایدهٔ اصلی حساب دیفرانسیل، بخش اول آنالیز ریاضی است که نرخ تغییرات تابع را نشان میدهد. مشتق نیز، نظیر انتگرال، از مسئلهای در هندسه، یعنی یافتن خط مماس در یک نقطه از منحنی ناشی شدهاست.
مفهوم مشتق تا اوائل قرن ۱۷ میلادی، یعنی تا قبل از آنکه ریاضیدان فرانسوی، پییر دو فرما به تعیین اکسترممهای چند تابع خاص دست بزند، تنظیم نشده بود. فرما دریافت که خطوط مماس، در نقاطی که منحنی ماکزیمم یا مینیمم دارد، باید افقی باشد. از اینرو به نظرش رسید که مسئلهٔ تعیین نقاط اکسترمم تابع، به حل مسئلهٔ دیگر، یعنی یافتن مماسهای افقی مربوط میشود، تلاش برای حل این مسئلهٔ کلیتر بود که فرما را به کشف برخی از ایدههای مقدماتی مفهوم مشتق هدایت کرد.
در نگاه نخست اینطور به نظر میرسید که بین مسئلهٔ یافتن مساحت سطح زیر یک نمودار و موضوع تعیین خط مماس بر منحنی در یک نقطه رابطهای وجود ندارد، اما اولین کسی که دریافت این دو مفهومِ به ظاهر دور از هم، در واقع ارتباط نسبتاً نزدیکی با هم دارند آیزاک بارو معلم آیزاک نیوتون بودهاست.
اما مفهوم مشتق به شکل امروزی آن، نخستین بار در سال ۱۶۶۶ میلادی توسط نیوتون و به فاصلهٔ چند سال بعد از او، توسط گوتفرید لایبنیتس، مستقل از یکدیگر پدید آمد. این دو دانشمند در ادامهٔ کار خود، باز هم بهطور مستقل، بخش دوم آنالیز ریاضی یعنی حساب انتگرال را عرضه کردند که اساس آن بر عمل انتگرالگیری قرار دارد.
نیوتون از شیوهٔ استدلال سینماتیک و با دیدگاه فیزیکی به بررسی مشتق پرداخته و از آن برای بدست آوردن سرعت لحظهای استفاده میکرد. اما لایبنیتس با دیدگاهی هندسی، از مشتق برای بدست آوردن ضریب زاویهٔ مماس در منحنیها استفاده میکرد. هر یک از این دو دانشمند نمادهای جداگانهای را برای نشان دادن مشتق به کار میبردند.
پیشرفت حساب دیفرانسیل و انتگرال در دوران بعد به آگوستَن لویی کوشی، برنهارد ریمان و برادران برنولی، یعنی یاکوب و یوهان، مربوط میشود. گیوم لوپیتال ، دانشمند فرانسوی، در سال ۱۶۹۶ نخستین کتاب درسی مربوط به آنالیز ریاضی را با نام «آنالیز بینهایت کوچکها برای بررسی منحنیها» منتشر کرد که در واقع خلاصهای از درسهایی بود که یوهان برنولی به عنوان معلم برای او نوشته بود. در این کتاب، قاعدهٔ رفع ابهام در حد، با استفاده از مشتق نیز آمده که به قاعدهٔ هوپیتال مشهور است ولی در واقع متعلق به یوهان برنولی بودهاست.
مشتق تابع
[ویرایش]اگر نقطهای از نمودار تابع و نقطهٔ دیگری از این نمودار باشد، آنگاه و شیب خط قاطع عبارت است از:
کسر فوق، خارج قسمت تفاضلی در نامیده میشود. اگر ثابت نگه داشته شود و به سمت صفر میل کند، آنگاه خارج قسمت تفاضلی در اگر فقط به بستگی داشته باشد به مقداری میل میکند که به آن شیب خط مماس گفته میشود. به عبارت دیگر، حاصل حد زیر در صورت وجود ضریب زاویهٔ خط مماس نمودار تابع در را بدست میدهد:
تعریف مشتق تابع
[ویرایش]برای تابع که در همسایگی نقطهٔ تعریف شدهاست، اگر وجود داشته باشد، در مشتقپذیر است. این حد (ریاضی) یکتا را با نمایش داده و آن را مشتق تابع در نقطهٔ مینامند.
بر طبق این تعریف، مقدار مشتق برابر نرخ تغییرات مقدار تابع است زمانی که تغییرات مربوط به متغیر مستقل به سمت صفر میل میکند.
با تبدیل به تعریف دوم مشتق به صورت زیر حاصل میشود:
نمادهای مشتق
[ویرایش]لایبنیتس، نیوتون، لاگرانژ، آربوگاست و اویلر هر یک نماد جداگانهای را برای نمایش مشتق بکار میبردند؛ اما در میان پیشگامان اولیهٔ آنالیز ریاضی، لایبنیتس بیش از هر کس دیگری به اهمیت علامات مناسب پی برده بود. او علامات را با حوصلهٔ زیادی آزمایش میکرد و با سایر ریاضیدانان مکاتبات بسیاری داشت و از این طریق معایب و محاسن نمادهای مختلف را برای آنها مطرح میساخت. پیشرفت حساب دیفرانسیل و انتگرال و گسترش ریاضیات نوین تا حدود زیادی بواسطهٔ علامتهای پیشرفتهای است که بسیاری از آنها توسط لایبنیتس ابداع شدهاند.
لایبنیتس در سال ۱۶۷۵ میلادی با استفاده از عملگر تفاضلی خارج قسمت تفاضلی را به شکل نوشت و برای مشتق تابع در نماد را معرفی کرد که به صورت نیز نوشته میشود. این نماد که نمایش دیفرانسیلی مشتق نامیده میشود، برای نمایش مشتق مراتب بالاتر به شکل نوشته میشود. با استفاده از این نماد تعریف مشتق به صورت در میآید.
نیوتون برای نشان دادن مشتق اول از و برای مشتق دوم از استفاده میکرد. نمادهای نقطهدار نیوتون در برخی مسائل فیزیکی مانند سرعت و شتاب بکار میروند.
مشتق تابع را با نیز میتوان نشان داد. این نماد بر آن تأکید دارد که تابع جدیدی است که با مشتقگیری از تابع بدست آمدهاست و مقدارش در با نموده میشود. مختصات و واقع بر نمودار با معادلهٔ به هم مربوط میشوند، و علامت نیز برای نمایش بکار میرود که مقدارش در به صورت نوشته میشود. این نماد در سال ۱۷۷۰ میلادی توسط ژوزف لویی لاگرانژ مورد استفاده قرار گرفت و مشتق مراتب بالاتر را به صورت (مشتق اول)، (مشتق دوم)، (مشتق سوم)، (مشتق چهارم) … (مشتق ام) نشان میدهد.
در سال ۱۸۰۰ میلادی نماد دیگری توسط لوییس آربوگاست معرفی شد و توسط لئونارد اویلر مورد استفاده قرار گرفت. این نماد مشتق را به شکل نشان میدهد. علامت یک عملگر دیفرانسیلی است و این فکر را القا میکند که تابع جدیدی است که با مشتقگیری از بدست آمدهاست. مشتق مراتب بالاتر به صورت و مقدار آن در به صورت نوشته میشود.
مشتقپذیری
[ویرایش]
تابع در مشتقپذیر است هرگاه در این نقطه پیوسته باشد و مشتق چپ و راست تابع با هم برابر و مساوی یک عدد حقیقی معین باشد.
تعبیر هندسی مشتقپذیری: تابع در مشتقپذیر است هرگاه بتوان در این نقطه یک خط کامل مماس و غیر موازی با محور yها بر منحنی رسم کرد.
اگر تابع در نقطهٔ مشتقپذیر باشد، آنگاه در آن نقطه پیوسته نیز هست.
ولی عکس قضیهٔ فوق صحیح نمیباشد یعنی ممکن است تابع پیوسته باشد اما مشتقپذیر نباشد؛ به عبارت دیگر، پیوستگی تابع در شرط لازم برای مشتقپذیری تابع است، نه شرط کافی. پس اگر تابع در ناپیوسته باشد، آنگاه در مشتقپذیر نیست.
موارد مشتقناپذیری
[ویرایش]
مواردی که تابع در نقطهٔ مفروض مشتقپذیر نیست:
- نقاط ناپیوسته: تابع در نقاط ناپیوسته مشتقناپذیر است و از دید هندسی نمیتوان در این نقاط مماس بر منحنی رسم کرد.
- نقاط زاویهدار: تابع در نقاط پیوستهای که مشتق چپ و راست در آنها دو عدد حقیقی نابرابر، یا یکی عدد و دیگری بینهایت باشد، مشتقپذیر نیست. از دید هندسی، در این نقاط دو نیممماس بر منحنی رسم میشود که با هم زاویه میسازند.
- نقاط عطف قائم: تابع در نقاط پیوستهای که مشتق چپ و راست در آنها بینهایتهای همعلامت باشد مشتقناپذیر است. از دید هندسی، در این نقاط میتوان یک خط کامل مماس به موازات محور yها رسم کرد. نقطهٔ عطف قائم تنها نقطهای است که تابع در آن مشتقپذیر نیست ولی مماس کامل دارد.
- نقاط بازگشت: تابع در نقاط پیوستهای که مشتق چپ و راست در آنها بینهایتهای غیر همعلامت باشد مشتقناپذیر است. از دید هندسی، در این نقاط میتوان یک نیممماس، به موازات محور yها رسم کرد.
- تابع در نقاطی که پیوستهاند ولی مشتق در آنها به سمت عدد مشخصی میل نمیکند نیز مشتقناپذیر است. از دید هندسی، در این نقاط نمیتوان مماس مشخصی بر منحنی رسم کرد.
مشتق مراتب بالاتر
[ویرایش]اگر تابع روی بازهٔ مشتقپذیر باشد تابع خود ممکن است در نقطهای مثل مشتقپذیر باشد. به عبارتی اگر موجود باشد، میگوییم مشتق مرتبهٔ دوم تابع در موجود است و آن را با نمایش میدهیم.
مشتق مراتب بالاتر یک تابع، از تعریف اصلی مشتق بدست میآید. بهطوریکه با مشتق گرفتن از مشتق اول تابع به مشتق دوم آن میرسیم و به همین ترتیب مشتق مراتب بالاتر نیز تعریف میشوند. به صورت کلی داریم:
مشتق nام چند تابع مهم
[ویرایش]مشتق ام چند تابع مهم نسبت به که و اعداد ثابت هستند:
قاعدهٔ لایبنیتس
[ویرایش]قاعدهٔ لایبنیتس بیان میکند که اگر دو تابع و روی بازهٔ دارای مشتقهای متوالی تا مرتبهٔ باشند، آنگاه حاصلضرب نیز روی این بازه دارای مشتقهای متوالی تا مرتبهٔ است و داریم:
منابع
[ویرایش]ویکی پدیای فارسی
انتگرال حجمی
یک انتگرال حجمی یا انتگرال سه گانه در ریاضی مورد خاصی از حساب انتگرال چند بعدی است که عمدتاً در فیزیک کاربرد پیدا می کند. این انتگرال سطحی را به یکپارچگی در هر دامنه ادغام سه بعدی گسترش می دهد، که در آن یک تابع سه بار پشت سر هم، هر کدام بر روی مختصاتی از سه ادغام می شود. -بعدی فضا. با این حال، این لزوماً نباید حجم یک جسم هندسی باشد. برای سادگی، اغلب فقط یک علامت انتگرال نوشته می شود و ادغام حجم فقط با عنصر حجم نشان داده می شود: :
جایی که تابعی که باید ادغام شود به حداقل سه متغیر برای توصیف (دکارتی) در فضای سه بعدی در اینجا دو معنی دارد، یک بار در عنصر حجم و یک بار به عنوان یک شناسه برای حجمی که یکی در آن ادغام،دامنه ادغام می شود.
در سیستم مختصات های سه بعدی
[ویرایش]همچنین برای دستگاه مختصات استوانهای داریم:
و برای دستگاه مختصات کروی داریم:
منابع
[ویرایش]https://de.m.wikipedia.org/wiki/Volumenintegral
توابع مثلثاتی
در ریاضیات، منظور از توابع مثلثاتی شش تابع سینوس، کسینوس، تانژانت، کتانژانت، سکانت و کسکانت است که این توابع رابطهٔ میان زاویهها و ضلعهای یک مثلث قائمالزاویه را نشان میدهند و به همین دلیل توابع مثلثاتی نامیده میشوند. قدمت اولین متنهای بهجامانده از توابع مثلثاتی به دوران پیش از میلاد در مصر و یونان بازمیگردد. قضیهٔ تالس توسط تالس در سدهٔ ششم پیش از میلاد در مصر مطرح شد، همچنین از قضیهٔ فیثاغورس به عنوان سنگ بنای مثلثات یاد میشود. علاوه بر مصر و یونان، کشورهای دیگری از جمله چین، هند، کشورهای اسلامی و کشورهای اروپایی پیشبردهای مطرحی در زمینهٔ مثلثات داشتند که میتوان به افرادی چون خوارزمی، بتانی، ابوالوفا محمد بوزجانی، شن کو، گو شوجینگ و رتیکوس اشاره کرد.
تعاریف متفاوتی از توابع مثلثاتی بیان شدهاست، سادهترین آنها بر پایهٔ دایرهٔ واحد است که در این تعریف دایرهای با شعاع ۱ ترسیم میشود و شعاعی با زاویهٔ مشخص نسبت به محور افقی روی آن رسم شده و یک مثلث را تشکیل میدهد. هر یک از توابع مثلثاتی را میتوان با پارهخطی در این دایره نشان داد. تعاریف دیگری از توابع مثلثاتی نیز بر پایهٔ انتگرال، سری توانی و معادلهٔ دیفرانسیل بیان شدهاست که هر یک از آنها کاربرد خاص خود را دارند. برای نمونه در تعریف بر پایهٔ سری توانی، از سری مکلورن استفاده میشود که در محاسبهٔ مقدار تقریبی آنها توابع مثلثاتی استفاده فراوان دارد.
توابع مثلثاتی بر روی یک زاویه عملیات انجام میدهند و یک عدد حقیقی را برمیگردانند و هر یک از آنها ویژگیهای خاص خود را دارند، از جمله زوج یا فرد بودن، متناوب بودن، پیوسته بودن، متعامد بودن. کاربرد اصلی این تابعها در محاسبهٔ اندازهٔ ضلعها و زاویههای یک مثلث و سایر عوامل مرتبط با آنها است. این کاربرد، در دانشهای مختلفی مانند نقشهبرداری، ناوبری و زمینههای گوناگون فیزیک مورد استفاده قرار میگیرد. در نقشهبرداری، با استفاده از اندازهگیری زاویهٔ یک نقطه نسبت به دو نقطه معین، مختصات آن نقطه را محاسبه میکنند که امروزه از این روش برای اندازهگیری سهبعدی نوری استفاده میشود یا در ناوبری، تنظیم خط سیر کشتیها و سایر شناورها بر پایهٔ اجسام ثابت مانند فانوس دریایی با بهرهگیری از توابع مثلثاتی انجام میشود. همچنین به علت خاصیت تناوبی بودن این تابعها، از آنها در مدلسازی فرایندهای نوسانی مانند نور و موج استفاده میشود. برای نمونه قانون اسنل بنیادیترین کاربرد توابع مثلثاتی است که در پدیدهٔ شکست نور به کار میرود. از دیگر کاربردهای توابع مثلثاتی میتوان به استفاده آن در صنعت برق و مخابرات اشاره کرد. از جمله کاربرد امواج سینوسی در جریانهای متناوب و همچنین انواع مدولاسیون که برپایه همین امواج سینوسی انجام میشود.
مقدمه
[ویرایش]قضیه فیثاغورس
[ویرایش]تشابه دو مثلث
[ویرایش]تاریخ
[ویرایش]تعاریف
[ویرایش]تعریف برپایه مثلث قائم الزاویه
[ویرایش]تعریف برپایه انتگرال
[ویرایش]تعریف برپایه سری توانی
[ویرایش]تعریف برپایه حساب دیفرانسیل
[ویرایش]ویژگی ها
[ویرایش]دور معکوس
[ویرایش]دور معکوس توابع مثلثاتی،که با نشان اختصاری(arc)که واژه مخفف(arcus)آن را نشان می دهند.این توابع،توابع معکوس مثلثاتی است که در صفحه بعد با آن سر و کار داریم.
تعریف
[ویرایش]توابع مثلثاتی تناوبی هستند، و بنابراین تزریقی نیستند، بنابراین به طور دقیق، تابع معکوس ندارند . با این حال، در هر بازهای که یک تابع مثلثاتی یکنواخت است ، میتوان یک تابع معکوس تعریف کرد و این توابع مثلثاتی معکوس را به عنوان توابع چند ارزشی تعریف میکند . برای تعریف یک تابع معکوس واقعی، باید دامنه را به بازهای محدود کرد که در آن تابع یکنواخت است و بنابراین از این بازه به تصویر آن توسط تابع دوگانه است. انتخاب رایج برای این بازه، مجموعه مقادیر اصلی نامیده می شود، در جدول زیر آورده شده است. طبق معمول، توابع مثلثاتی معکوس با پیشوند "قوس" قبل از نام یا مخفف آن تابع کار کرد نشان داده می شوند.انتخاب رایج برای این بازه، که مجموعه مقادیر اصلی نامیده می شود، در جدول زیر آورده شده است. طبق معمول، توابع مثلثاتی معکوس با پیشوند "قوس" قبل از نام یا مخفف آن تابع نشان داده می شوند.
| تایع | تعریف | دامنه | مجموعه ای از مقادیر اصلی |
|---|---|---|---|
قضیه
[ویرایش]نمادهای sin^-1 ، cos^-1 ، و غیره اغلب برای arcsin و arccos و غیره استفاده میشوند. وقتی از این نمادها استفاده میشود، ممکن است خواننده توابع معکوس را با معکوسهای ضربی اشتباه بگیرد. علامتگذاری با پیشوند "arc" از چنین سردرگمیای جلوگیری می کند، اگرچه "arcsec" برای arcsecant را می توان با "arcsecond" اشتباه گرفت. درست مانند سینوس و کسینوس، توابع مثلثاتی معکوس را نیز می توان بر حسب سری نامتناهی بیان کرد. همچنین می توان آنها را بر حسب لگاریتم های پیچیده بیان نمود.
روش محاسبه
[ویرایش]اتحادها و مقادیر جبری
[ویرایش]برحسب رادیان
[ویرایش]منابع
[ویرایش]- حساب دیفرانسیل و انتگرال وهندسه تحلیلی/نوشته ریچارد ا.سیلورمن/ترجمه:دکتر علی اکبر عالم زاده/۱۴۰۱
- حساب دیفرانسیل و انتگرال/جیمز استوارت/انتشارات دانشگاه فاطمی/۱۳۸۸
- ویکی پدیای فارسی
- ویکی پدیای انگلیسی
آزمون دینی
در ریاضیات، آزمون دینی آزمونی است برای تعیین همگرایی نقطه ای یک سری فوریه. این آزمون نخستین بار بوسیله ریاضیدان ایتالیایی اولیسه دینی در سال ۱۸۸۰ معرفی شد.
گزاره
[ویرایش]فرض کنید یک تابع موضعا انتگرالپذیر متناوب و باشد. اگر عددی حقیقی همچون و یک موجود باشد که ، آنگاه سری فوریه در نقطه به همگرا خواهد بود.
آزمون دینی به یک معنا در قویترین حالت ممکن است: اگر تابعی متناوب باشد که در نقطه موضعا انتگرالپذیر نباشد، آنگاه تابع با تناوب موجود است که برای هر ولی سری فوریه در واگراست.
منابع
[ویرایش]ویکیپدیای فارسی
انواع هندسه
هندسه اقلیدوسی
[ویرایش]
هندسه اقلیدوسی یک دستگاهی ریاضیاتی از هندسه است که آن را به ریاضیدان یونانی،اقلیدوس نسبت داده اند،چون اقلیدوس در کتاب خود به اسم اصول اقلیدوس به این نوع هندسه اشاره و توصیف کرده است.این هندسه شامل هندسه فضایی نیز می گردد
تمامِ هندسهٔ اقلیدسی، میتواند از پنج اصلِ موضوعهٔ زیر استخراج شود:
- از هر دو نقطه متمایز، یک و تنها یک خط راست میگذرد.
- هر پارهخط را میتوان تا بینهایت رویِ خطِ راست امتداد داد.
- با یک نقطه به عنوانِ مرکز و یک پارهخط به عنوانِ شعاع میتوان یک دایره رسم نمود.
- همهٔ زوایایِ قائمه با هم برابرند. (این اصل معیاری طبیعی برای اندازهگیری زاویهها در اختیار میگذارد)
- اگر یک خط، دو خطِ دیگر را قطع کند، آن دو خط در طرفی که جمعِ زوایایِ داخلیِ تولید شده توسطِ خطِ مورب کمتر از دوقائمه است به هم میرسند (خود یا امتدادشان).
هندسه فضایی
[ویرایش]ر ریاضیات،هندسه فضایی یا هندسه سه بعدی،نوعی هندسه اقلیدوسی است که به فضای حجمی یا سه بعدی اطلاق می شود.این هندسه برای آشنایی با احجام هندسی،احجام چندوجهی و... و مقاطع مخروطی،فضای سه بعدی،مختصات کروی،استوانه ای،حجم،مساحت و... است.
حجم های هندسی به اجسام هایی گفته میشود که برای آنها میتوانیم برای آنهافرمول سطح و حجم بنویسیم.حجم آن اجسام هندسی را میتوانیم به روش الگویابی با استفاده از تجزیه و تحلیل و اندازه گیری حجم اجزای متناظر و جمع بندی و فرمول بندی آن میتوان فرمول حجم آن را بدست آورد.برای پیدا کردن مساحت آن ابتدا با تجزیه و گسترده کشیدن شکل به روش پیوسته و گسسته مساحت اجزای آن را حساب میکنیم و با آنالیز فرمول آن را مینویسیم.
در ریاضیات فضای سه بعدی فضای برداری دارای سه بعد و یک مدل هندسی از جهان فیزیکی است که در آن زندگی میکنیم. ابعاد سهگانه معمولاً به نام طول، عرض، و ارتفاع (یا عمق) شناخته میشوند اگر چه این نامگذاری اختیاری است.
هندسه نااقلیدسی
[ویرایش]هندسه نااقلیدوسی به مطالب عمین تر و گسترده تر از هندسه اقلیدوسی می پردازد و شامل موارد های هندسی جدید مثل هندسه کروی،البته مطالب هندسه نا اقلیدوسی به مطالب هندسه اقلیدوسی به صورتی عمیق تر بررسی می کند.
هندسهٔ نااقلیدسی بعدها توسط گاوس و ریمان در قالب هندسهٔ کلّیتری بسط داده شدند. همین هندسهٔ کلیتر است که در نگرهٔ نسبیت عام اینشتین استفاده شدهاست. در هندسه نااقلیدوسی مجموعه زوایای داخلی مثلت ۱۸۰درجه نمیباشد. برای مثال اگر ضلعهای مثلث هذلولوی باشد مجموعه زوایای داخلی هیچگاه به۱۸۰درجه نمیرسد و کمتر میباشد. همچنین اگر هندسه بیضوی باشد، هیچگاه ۱۸۰ درجه نمیشود؛ بلکه بیشتر میباشد.
هندسه ریمانی
[ویرایش]
هندسه ریمانی شاخه ای از هندسه دیفرانسیل است که به بررسی و مطالعه مطالب منیفلدهای ریمانی می پردازد، یعنی منیفلدهای هموار مجهز به متریک ریمانی، این ساختار منیفلد را در هر نقطه مجهز به ضرب داخلی روی فضای مماس می کند، به طوری که از نقطهای به نقطه دیگر به طور هموار تغییر میکند. همچنین این ساختار به طور خاص مفاهیم موضعی چون زاویه، طول خم، مساحت رویه و حجم را بدست می دهد. از اینها، برخی از سایر کمیّتهای سرتاسری را می توان به وسیله انتگرالگیری بدست آورد.
هندسه ریمانی اولین بار به طور کلی توسط برنهارد ریمان در قرن نوزدهم مطرح شد. با طیف وسیعی از هندسهها سروکار دارد که ویژگیهای متریک آنها از نقطهای به نقطه دیگر متفاوت است، از جمله انواع استاندارد هندسه غیراقلیدسی . هر منیفولد صاف یک متریک ریمانی را می پذیرد که اغلب به حل مسائل توپولوژی دیفرانسیل کمک می کند . همچنین به عنوان سطح ورودی برای ساختار پیچیدهتر منیفولدهای شبه ریمانی ، که (در چهار بعد) اشیاء اصلی نظریه نسبیت عام هستند، عمل میکند. از دیگر تعمیم هندسه ریمانی می توان به هندسه فینسلر اشاره کرد.
هندسه جبری
[ویرایش]هندسهٔ جبری شاخهای از ریاضیات است که بهطور سنتی به مطالعهٔ صفرهای چندجملهایهای چند متغیره میپردازد. هندسهٔ جبری مدرن بر اساس استفاده از تکنیکهای جبر مجرد بنا شده که اساساً از جبر جابجایی استفاده میکند تا مسائل هندسی مربوط به این مجموعه صفرها (ریشه این چند جملهایها) را مطالعه کند.
هندسه تحلیلی
[ویرایش]هندسه تحلیلی شاخهای از ریاضیات است که از ترکیب هندسه و جبر مقدماتی به وجود آمدهاست. در این رشته اشکال هندسی و روابط بین آنها را با مقادیر و معادلات عددی و جبری و اتحادی بیان میکنند.
بنیانگذاران این مبحث در اروپا ، دکارت و فرما در قرن ۱۷ میلادی بودهاند.
رایجترین سیستم مختصاتی در هندسه تحلیلی که استفاده در فضای دوبعدی میشود، سیستم مختصات دکارتی است ، که در آن هر نقطه دارای یک مختصات x است و گاهی هم مختصاتyاست.در معادله خطی هم از مختصات دکارتی استفاده می کنیم،که موقعیت افقی آن را نشان میدهد و یک مختصات y که موقعیت عمودی آن را نشان میدهد. اینها معمولاً به صورت یک جفت مرتب شده ( x , y ) نوشته می شوند. این سیستم همچنین می تواند برای هندسه سه بعدی استفاده شود، که در آن هر نقطه در فضای اقلیدسی با یک سه مرتبه مختصات ( x ، y ، z ) نشان داده می شود.در مختصات درکارتی موارد برداری هم تعریف می گردد.
هندسه دیفرانسیلی
[ویرایش]هندسه دیفرانسیل یک مبحث ریاضیاتی پیشرفته است که به بررسی و مطالعه هندسه اشکال صاف و فضاهای صاف به همراه مختصات آنها بر اساس انحنا آنها می پردازد که در غیر این صورت منیفولدهای صاف نامیده می شوند.هندسه دیفرانسیل به کمک هندسه ریمانی به بررسی مینفولدهای خم و پیچیده می پردازد.از تکنیک های حساب دیفرانسیل ، حساب انتگرال ، جبر خطی و جبر چند خطی و هندسه فضایی،هندسه تحلیلی،آنالیز ریاضی و...استفاده می کند. ریشه این رشته در مطالعه هندسه کروی از دوران باستان است. همچنین به نجوم ، ژئودزی زمین و بعدها مطالعه هندسه هذلولی توسط لوباچفسکی مربوط می شود .. سادهترین نمونههای فضاهای صاف، منحنیها و سطوح صفحه و فضا در فضای سهبعدی اقلیدسی هستند و مطالعه این اشکال مبنای توسعه هندسه دیفرانسیل مدرن در قرنهای 18 و 19 بود.
هندسه دیفرانسیل در سراسر ریاضیات و علوم طبیعی کاربرد دارد(مثل:ساختار مهندسی در معماری مخروطی و کروی و ساختار جغرافیایی مثل کوها وپزشکی در دستگاه رادیولوژی). زبان هندسه دیفرانسیل بیشتر توسط آلبرت انیشتین فیزیکدان و ریاضیدان آمریکایی در نظریه نسبیت عام و متعاقباً توسط فیزیکدانان در توسعه نظریه میدان کوانتومی و مدل استاندارد فیزیک ذرات مورد استفاده قرار گرفت. خارج از فیزیک، هندسه دیفرانسیل در شیمی ، اقتصاد ، مهندسی ، تئوری کنترل ، گرافیک کامپیوتری و بینایی کامپیوتر و اخیراً در یادگیری ماشین کاربرد دارد.
هندسه تصویری
[ویرایش]
هندسه تصویری شاخه از ریاضیات و هندسه است که اشکال هندسی و روابط قضیه هندسی را به صورت ترسیم تصویر نمایش می دهد.این نوع ترسیم نوعی تصویرخوانی ریاضی-هندسی است.
رابطه فیثاغورس طبق مفاهیم(a2=b2+c2)است طبق تصویر هندسی زیر این رابطه به صورت مربعی شکل است
مساحت و حجم
سطحوحجم(بهانگلیسیArea&Volume) مبحثی از علمهندسهفضایی است کهدر مورد خواص،ویژگی،کاربرد و محاسبه حجم ومساحت احجام هندسی سه بعدی میپردازد.احسام سهبعدی به اجسامی گفته میشوند که دارای سهبعد(طول،عرض،ارتفاع)است.
دَوَران،مَقطَع،بُرش،رسم سهنما،رسم گسترده احجام،مُحاط کردن،حجم ومساحت از عناصر مهم این علم است.
حجم های هندسی به دو دسته تقسیم میشوند:
- حجم های هندسی مثل منشور، کره،هرم، ...
- حجم های غیرهندسی
زندگی نامه کاشفان در زمینه سطح و حجم
[ویرایش]ارشمیدوس یک دانشمند،فیلسوف،ریاضیدان،هندسه دان، فیزیک دان،مخترع،ستاره شناس و مهندس یونانی است که در سال ۲۸۷ق.م در شهر سیراکوز و در سال۲۱۲ق.م در همان شهر در ۷۵سالگی از دنیا رفت. او در زمینه ریاضیات کارهای مهمی انجام داده است. او توانست مساحت و حجم استوانه،مخروط و کره را محاسبه کند و عدد پی را با دقت محاسبه کند و توانست نسبت حجم و مساحت کره را به حجم و مساحت استوانه بدست آورد و حتی او توانست نسبت V/S احجام را محاسبه کند.جایگاه وی در زمینه ریاضیات بالا است.
تعریف ها
[ویرایش]تعریف مساحت و حجم
[ویرایش]حجم: به مقدار فضایی که یک جسم اشغال میکند حجم میگویند. واحد حجم برابر با واحد مکعب است.حَجم کمیتی از فضای سهبعدی است که با یک مرز مشخص محدود شدهاست برای نمونه فضای اشغالی یک ماده (جامد، گاز، مایع، پلاسما) یا شکل آن است.حجم، یک یکای فرعی اسآی است که واحد آن، متر به توان ۳ (متر مکعب) میباشد. میزان حجم یک ظرف، برابر است با حجم سیالی که آن را پر میکند. برای محاسبه حجم، شکلهای ۳ بعدی خاص، روابط مشخصی وجود دارد که برای شکلهای ساده دارای نظم هندسی، روابط ساده هستند. برای شکلهای پیچیده نیز که رابطهی سادهای برای محاسبه حجم، وجود ندارد از روشهای انتگرالی میتوان حجم را بهدست آورد. حجم شکلهای یکبعدی، مانند خط یا دوبعدی، مانند صفحه، صفر میباشد.
مساحت:نوعی کمیت است که مقدار سطح رویه اجسام سه بعدی و مقدار درونی اجسام دوبعدی را محاسبه میکند واحد مساحت برابر با واحدمربع است.مساحت کمیتی است که وسعت یک ناحیه را روی صفحه یا روی یک سطح منحنی بیان می کند. مساحت ناحیه صفحه یا مساحت صفحه به مساحت یک لایه یا لایه مسطح اشاره دارد ، در حالی که مساحت سطح به مساحت یک سطح باز یا مرز یک جسم سه بعدی اشاره دارد . مساحت را می توان به عنوان مقدار ماده ای با ضخامت معین که برای شکل دادن به مدلی از شکل لازم است یا مقدار رنگ لازم برای پوشاندن سطح با یک لایه درک کرد. این آنالوگ دو بعدی طول یک منحنی (یک مفهوم یک بعدی) یا حجم یک جامد (یک مفهوم سه بعدی) است.
تعریف احجام هندسی و غیرهندسی
[ویرایش]حجم های غیر هندسی= حجم های غیر هندسی به حجم های پیچیده گفته میشود که حجم های آن سخت بدست آید. اما مساحت آنها را میتوان بدست آورد اما کمی پیچیده است.برای بدست آوردن حجم های غیرهندسی ابتدا در یک لیوان بشر،آب میریزیم.بعد که پر از آب کردیم و مقدار لیتر را اندازه گیری کردیم؛جسم غیر هندسی را در آب میاندازیم با این روش آب بالا میآید، بعد مقدار آبی که با حجم غیر هندسی بالا آمده است را با مقدار آبی که قبل تعیین شد کم میکنیم و بعد حجم آن را اندازه گیری و مینویسیم.
حجم های هندسی= حجم های هندسی به اجسام هایی گفته میشود که برای آنها میتوانیم برای آنهافرمول سطح و حجم بنویسیم.حجم آن اجسام هندسی را میتوانیم به روش الگویابی با استفاده از تجزیه و تحلیل و اندازه گیری حجم اجزای متناظر و جمع بندی و فرمول بندی آن میتوان فرمول حجم آن را بدست آورد.برای پیدا کردن مساحت آن ابتدا با تجزیه و گسترده کشیدن شکل به روش پیوسته و گسسته مساحت اجزای آن را حساب میکنیم و با آنالیز فرمول آن را مینویسیم.
مثال= کره،هرم،منشور،چندوجهی،استوانه،مخروط و مکعب،چهاروجهی،متوازی السطوح
نکاتی در مورد حجم های هندسی
[ویرایش]نکته۱: مکعب یک چندوجهی(شش وجهی) منتظم دارای وجه مربع است که دارای دو قاعده مربع است پس مکعب یک حجم چند وجهی- منشوری منتظم است.
نکته۲: چهاروجهی یک هرم و چندوجهی با قاعده و وجه های مثلث متساوی الاضلاع است. پس چهاروجهی یک حجم هرمی-چندوجهی و نوعی جسم افلاطونی به حساب می آید.
نکته۳: متوازی السطوح یک حجم منشوری دارای وجه جانبی و دوقاعده است و یک شش وجهی با وجه های متوازی الاضلاع است.پس متوازی السطوح یک حجم منشوری-چندوجهی است.
تعریف منشور، کره و هرم
[ویرایش]تعریف منشور:منشور حجمی است که دارای دو قاعده وجه جانبی،راس و یال است .وجه های منشور مستطیلی است و تعداد وجه های آن با تعداد ضلع قاعده اش برابر است،تعداد راس های آن دو برابر وجه و تعداد یال سه برابر وجه منشور است.وجه های هرم با فرمولn+2بدست می آیو چون تعداد وجه هاب منشور همیشه دو تا بیشتر از وجه جانبی است چون دو وجه دیگر قاعده منشور هستند.منشور درهندسه،یک چندوجهی است که با یک قاعدهٔ n-ضلعی، انتقالیافتهٔ چندضلعی قاعده (درصفحهای دیگر) و n وجه دیگر که لزوماً همه متوازیالأضلاع بوده و رأسهای متناظر دو n-ضلعی را به هم متصل میکنند. همهٔ سطح مقطعهای موازی با قاعده، یکسان هستند. منشورها با توجه به تعداد اضلاع قاعدهشان نامگذاری میشوند؛ بنابراین بهعنوان مثال، یک منشور با قاعدهٔ پنجضلعی، منشور پنجضلعی نامیده میشود.در تعریف منشور به هرم این است که منشور همان هرم است ولی راس آن در بی نهایت قرار دارد
تعریف هرم:هرم حجمی است که وجه های آن در یک نقطه قطع میشود و وجه های آن مثلثی شکل است که دارای یک قاعده است.وجه های هرم با فرمولn+1بدست می آید چودن هرم دارای یک راسی اضافه است.تعداد یال های هرم دوبرابر تعداد ضلع قاعده است.درواقع هرم شکلی سهبعدی است که از اتصال نقطهای در فضا به تمام نقاط شکلی بسته در صفحه به وجود میآید. به آن نقطه، رأس هرم و به آن شکل مسطح، قاعده هرم گفته میشود. قاعده هرم، چندضلعی دلخواه است و سایر وجهها مثلثهایی هم راس هستند که در رأس به یکدیگر متصل میشوند. خط قائمی که رأس را به قاعده متصل میکند، ارتفاع هرم نامیده میشود. از معروف ترین سازه های جهان به شکل هرم ،می توان به اهرام ثلاثه مصر اشاره کرد.
تعریف کره:کره یک جسم هندسی کاملاً گرد در فضای سه بعدی است. برای نمونه توپ یک کره است. کره مانند دایره که در دو بعد است، در فضای سه بعدی یک کاملاً متقارن در گرداگرد یک نقطهاست. تمام نقاطی که بر سطح کره جای دارند در فاصلهٔ یکسان از مرکز کره قرار دارند. فاصلهٔ این نقطهها از مرکز کره، شعاع کره نام دارد و با حرف r نمایش داده میشود. بلندترین فاصله از دو سوی کره (که از درون کره عبور کند) قطر کره نام دارد. قطر کره از مرکز آن نیز میگذرد و در نه نتیجه اندازهٔ آن دو برابر شعاع است. ،کره مجموعه نقاطی از فضا است که دارای شعاع و قاعده دایره ای شکل است که یک چند وجهی منتظم است.کره حاصل دوران یک نیم دایره و دایره حول قطر است که در دایره به اندازه ۱۸۰درجه می چرخد و در نیم دایره به اندازه۳۶۰درجه میچرخد.وجه های کره بر اساس تقسیمی از مساحت آن که۳۶۰ درجه است به چندین درجه تقسیم میکنیم.
تعریف استوانه،مخروط وچندوجهی
[ویرایش]تعریف استوانه:استوانه یک حجم منشوری است که قاعده آن به صورت دایره ای شکل است.استوانه در هندسه یک پایه منحنی فضایی است که دور سطح آن را مجموعه نقاطی تشکیل داده است.یال های استوانه همان نامشخص است چون قاعده آن به صورت دایره ای است،می توان گفت که وجه جانبی،وجه،راس،یال استوانه به ترتیب3n,2n,n+2,nاست.استوانه درهندسه دیفرانسیل به صورت یک سطح کشیده است که که مولد آن یک دسته خط موازی است.تعریف استوانه در مخروط این است که استوانه همان مخروط است ولی راس آن در بی نهایت قرار دارد.استوانه حاصل دوران یک مستطیل حول یکی از اضلاع آن(طول،عرض) به اندازه۳۶۰درجه می باشد.
تعریف مخروط:مخروط یک حجم هرمی می باشد که قاعده آن به صورت دایره ای است،یک مخروط یک شکل هندسی سهبُعدی است که از پایهٔ تختش (سطح مقطع مخروط) به آرامی یا به سرعت (به سطح قاعده و ارتفاع بستگی دارد) تا راس باریک میشود. بهطور جزئیتر شکلی جامد است که به یک صفحهٔ پایه (سطح مقطع مخروط)، محدود میشود و سطح جانبی آن نیز مکان هندسی خطوط راستی است که نوک مخروط را به نقاط پیرامون پایه (سطح مقطع) پیوند میزنند. واژهٔ مخروط گاهی به رویهٔ این جسم توپر گفته میشود و گاه تنها به رویهٔ پهلویی آن است.مخروطها میتوانند به صورت قائم یا اریب باشند. لازم است ذکر شود که حجم یک مخروط اریب با مساحت سطح مقطع معین و ارتفاع مشخص، با حجم یک مخروط قائم با همان مساحت و ارتفاع معین، برابر است.مخروط حاصل دوران یک مثلث قائم الزاویه حول یکی از اضلاع مجاورش به اندازه۳۶۰درجه است.
تعریف چندوجهی:چندوجهی یک شیء صلب هندسی در فضای سه بعدی است که وجههایی صاف (هر وجه در یک صفحه) و ضلعها یا یالهایی واقع بر خط راست دارد. تا کنون تعریف واحدی برای آن ارائه نشدهاست. چهاروجهی از انواع هرم است و مکعب نمونهای از یک شش وجهی است. چندوجهی میتواند محدب یا غیر محدب باشد.چندوجهیهایی مثل هرم و منشور را با میتوان اکستروژن (بیرون کشیدن) چندضلعیهای دوبعدی ساخت. تنها تعداد محدودی از چندوجهیهای محدب با وجوه منتظم و شکل گوشههای برابر میتواند وجود داشته باشد که شامل اجسام افلاطونی و اجسام ارشمیدسی میشود. برخی اجسام ارشمیدسی را میتوان با بریدن هرم راس اجسام افلاطونی ساخت.به دلیل سادگی ساختن، در غالب آثار معماری مانند گنبدهای ژئودزیک و اهرام از چندوجهیها استفاده میشود. اخیراً نیز به علت استفاده از اشکال علاقه به سطوح چندوجهی افزایش یافتهاست. برخی مولکولها و اتمهای فشرده، بهویژه ساختارهای بلوری و هیدروکربنهای افلاطونی و همچنین برخی شعاعیان شکلی شبیه اجسام افلاطونی دارند. از اجسام افلاطونی در ساخت تاس نیز استفاده میشود.چندوجهیها ویژگیها و انواع گوناگونی دارند و در گروههای تقارنی مختلفی جای میگیرند. با اعمالی روی هر چندوجهی میتوان چندوجهیهای دیگری ساخت. بعضی از آنها با هم روابطی دارند. چندوجهیها از عصر حجر مورد توجه بودهاند.کره نیز از خانواده چندوجهی ها نیز به حساب می آید.مکعب،چهاروجهی،متوازی السطوح از احجام های هندسی هستند که چندوجهی نیز به حساب می آید.
مساحت و حجم اشکال هندسی
[ویرایش]حجم مکعب:
مساحت مکعب:
حجم چهار وجهی:
مساحت چهاروجهی:
حجم هشت وجهی منتظم:
مساحت هشت وجهی منتظم:
حجم مکعب مستطیل:
مساحت مکعب مستطیل:
حجم منشور:
حجم منشور با قاعده چندضلعی:
مساحت منشور با قاعده چندضلعی:
حجم استوانه:
مساحت منشور:
مساحت استوانه:
حجم هرم:
حجم مخروط:
مساحت هرم:
مساحت مخروط:
حجم کره:
مساحت کره:
حجم کره بیضی گون با قاعده دایره(کره گون):
حجم کره بیضی گون مختلف:
مساحت کره گون=
مساحت بیضی گون=:
حجم هرم ناقص:
مساحت هرم ناقص:
حجم مخروط ناقص:
مساحت مخروط ناقص: حجم چنبره:
مساحت چنبره:
حجم متوازی السطوح:
مساحت متوازی السطوح:
مساحت چندوجهی منتظم:
حجم جامدات چندوجهی:
حجم مکعب
[ویرایش]محاسبه حجم مکعب از طریق توان سوم اضلاع آن، توان سوم مکعب نامیده میشود همانطور که توان دوم مربع نامیده میشود.حجم آن به این صورت است:
محاسبه حجم مکعب به صورت مساحت چندضلعی منتظم
[ویرایش]مربع از نوع چندضلعی های منتظم است و از وجه های مکعب و قاعده مکعب مربع است.مساحت مربع همواره با فرمول مساحت چندضلعی برابر است.در اینجا:
مساحت
[ویرایش]مربع از نوع چندضلعی های منتظم است و از وجه های مکعب و قاعده مکعب مربع است.مساحت مربع همواره با فرمول مساحت چندضلعی برابر است.و مکعب از شش وجه مربع ساخته شده است و به همین از تشکیل وجه های چندضلعی منتظم،چندوجهی منتظم ساخته می شود.
مکعب نیز دارای مساخت کل نیز است.و مساحت آن برابر با این رابطه است:
اگر طبق مساحت چندضلعی حساب شود،به این صورت است.
در اینجا:
حجم مکعب
[ویرایش]محاسبه حجم مکعب از طریق توان سوم اضلاع آن، توان سوم مکعب نامیده میشود همانطور که توان دوم مربع نامیده میشود.حجم آن به این صورت است:
محاسبه حجم مکعب به صورت مساحت چندضلعی منتظم
[ویرایش]مربع از نوع چندضلعی های منتظم است و از وجه های مکعب و قاعده مکعب مربع است.مساحت مربع همواره با فرمول مساحت چندضلعی برابر است.در اینجا:
مساحت
[ویرایش]مربع از نوع چندضلعی های منتظم است و از وجه های مکعب و قاعده مکعب مربع است.مساحت مربع همواره با فرمول مساحت چندضلعی برابر است.و مکعب از شش وجه مربع ساخته شده است و به همین از تشکیل وجه های چندضلعی منتظم،چندوجهی منتظم ساخته می شود.
مکعب نیز دارای مساخت کل نیز است.و مساحت آن برابر با این رابطه است:
اگر طبق مساحت چندضلعی حساب شود،به این صورت است.
در اینجا:
حجم
[ویرایش]متوازی السطوح حجمی است که از سه بردار سه بعدی a,b,cدرست شده است و با ضرب خارجی بردار ها درست شده است.
محاسبه حجم
[ویرایش]ابتدا متوازی السطوحی رسم می کنیم که در فضای برداری باشد و در فضای سه بعدیR3قرار می دهیم.بردار های آن اینگونه است که:
محاسبه حجم اینگونه است مساحت قاعده بر اساس مساحت متوازی الاضلاع بدست آید و ارتفاع آن بر اساس رابطه فیثاغورس بدست آید.پس حجم متوازی السطوح برابر با این رابطه است.کسینوس تتا و سینوس تتا در محاسبه قدر مطلق برابر با یک می شود،قدرمطلق مساحت برداری هایa,b,cبرابر با خودشان است.
می توان به روش عمیق تری حجم آن را بدست آورد،ضرب داخلی بردار های خارجی که با ضرب خارجی این سه بردار متوازی السطوح را بدست آورند این گونه است.حجم برابر است
که همان برابر با این رابطه است.راه دیگر برای اثبات ( V1 ) استفاده از مولفه اسکالر در جهت استa×b
از بردار:a,b,cحجم متوازی السطوح به صورت مختصاتی برابر با این عبارت فوق است اما به روش دیگر هم که به صورا مختصاتی نوشته نمی گردد بلکه مثل حجم مکعب مستطیل است که برابر با ضرب طول بردار هاست ولی یک عبارتی لازم دارد.
نتیجه بر این است.
با استفاده از روش قدر مطلق و محاسبه ضرب داخلی و خارجی بردارها به مقداری به نامkنیاز است.kمقداری است که بر اساس زاویه های لبه متوازی السطوح بدست می آید.که به صورت جذر آن درحجم متوازی السطوح به کار می رود.
مقدار kبراساس این رابطه بدست می آید.مقدار جذر آن این گونه استحجم آن براساس این رابطه نوشته می گردد.که می توان این گونه نوشتکه برابر با حجم مختصاتی متوازی السطوح است.
مساحت
[ویرایش]مساحت یک متوازی السطوح براساس جمع مساحت شش متوازی الاضلاع بدست می آید که براساس این رابطه نوشته می گرددمساحت متوازی السطوح مثل مساحت مکعب مستطیل بدست می آید،مکعب،مکعب مستطیل از احجام منشوری است که به صورت برداری کشیده اند.
به صورت دیگر هم مساحت آن پیدا می گردد که به صورت مساحت متوازی الاضلاع بدست می آید
برای پیدا کردن مساحت متوازی السطوج بر اساس a,b,c اینگونه است.
hبرابر با ارتفاع متوازی السطوح است بر حسب تتا زاویه است که h بر اساس رابطه فیثاغورس نوشته میشود.
=مقداری است که بر اساس تتا زیر جزئی از طول های به ترتیب b,c است
اگر این دو رابطه را محاسبه کنیم به این نتیجه می رسیم
حجم
[ویرایش]حجم منشور اگرsمساحت قاعده و h ارتفاع باشد،حجم آن می شود:
مساحت
[ویرایش]مساحت جانبی منشور اگرpمحیط قاعده و hارتفاع باشد بر این اساس نوشته می شود.
مساحت کل منشور اگر s مساحت قاعده باشد می توان بر اساس این فرمول نوشت
حجم به صورت مثلثاتی
[ویرایش]حجم یک منشور حاصل ضرب مساحت قاعده و فاصله بین دو وجه قاعده یا ارتفاع است (در مورد منشور غیر راست توجه داشته باشید که این به معنای فاصله عمود بر هم است). که در آن B مساحت پایه و h ارتفاع است. حجم منشوری که قاعده آن یک چندضلعی منتظم n ضلعی با طول ضلع s است برابر است با:
مساحت به روش مثلثاتی
[ویرایش]مساحت سطح منشور راست 2 · B + P · h است که B مساحت قاعده، h ارتفاع و P محیط پایه است.
مساحت سطح یک منشور راست که قاعده آن یک چندضلعی n ضلعی منتظم با طول ضلع s و ارتفاع h است به این صورت است:
نسبت V/S منشور
[ویرایش]نسبت V/Sروشی است که نسبت حجم به سطح کل است
نسبتV/S منشور:
حجم
[ویرایش]قاعده یک استوانه به صورت دایره ای است و نوعی منشور به حساب می آید.
- مساحت دایره(قاعده):
- ارتفاع:
- حجم استوانه:
حجم یک استوانه طبق حجم منشور ها حساب می گردد چون استوانه منشوری است و دوقاعده دارد و دارای ارتفاع نیز هست و قاعده آن نیز دایره ای است پس طبق حجم منشور می نویسیم
حجم استوانه به روش انتگرالی
[ویرایش]به طور کلی، بر اساس همین اصل، حجم هر استوانه حاصل ضرب مساحت پایه و ارتفاع است. به عنوان مثال، یک استوانه بیضوی با پایه دارای محور نیمه اصلی a ، محور نیمه فرعی b و ارتفاع h دارای حجم V = Ah است که در آن A مساحت بیضی پایه (= π ab ) است. این نتیجه برای استوانه های بیضوی راست را می توان با ادغام نیز به دست آورد، که در آن محور استوانه به عنوان محور x مثبت و A ( x ) = A مساحت هر مقطع بیضوی در نظر گرفته می شود، بنابراین:یک جزء از حجم، استوانهٔ راستی است که قاعدهٔ آن مساحتی برابر با Awi دارد و ضخامتی برابر با Δix دارد. پس اگر V حجم استوانهٔ دایرهای راست باشد، با استفاده از جمعهای ریمانی داریم:
مساحت
[ویرایش]با داشتن شعاع r و ارتفاع (ارتفاع) h ، سطح یک استوانه دایره ای سمت راست، به گونه ای که محور آن عمودی باشد، از سه قسمت تشکیل شده است:
- مساحت پایه بالایی:
- مساحت پایه پایین:
- مساحت ضلع:
مساحت پایه های بالا و پایین یکسان است و مساحت پایه B نامیده می شود . مساحت ضلع به نام ناحیه جانبی ، L شناخته می شود.
یک استوانه باز شامل عناصر بالا و پایین نیست و بنابراین دارای سطح (منطقه جانبی) است.
مساحت استوانه دایره ای راست جامد از مجموع هر سه جزء بالا، پایین و جانبی تشکیل شده است. بنابراین مساحت سطح آن،
که در آن d = 2 r قطر بالا یا پایین مدور است .
برای یک حجم معین، استوانه دایره ای سمت راست با کوچکترین سطح دارای h = 2 r است. به طور معادل، برای یک سطح معین، استوانه دایره ای سمت راست با بیشترین حجم دارای h = 2 r است، یعنی استوانه به خوبی در یک مکعب به طول ضلع = ارتفاع (= قطر دایره پایه) قرار می گیرد.
مساحت جانبی، L ، یک استوانه دایره ای، که نیازی به استوانه سمت راست نیست، به طور کلی به صورت زیر نشان داده می شود:
که e طول یک عنصر و p محیط قسمت سمت راست استوانه است. این فرمول قبلی را برای مساحت جانبی زمانی که استوانه یک استوانه دایره ای راست است، تولید می کند.
حجم و مساحت مخروط
[ویرایش]حجم
[ویرایش]حجم یک هرم برابر بر این رابطه است که چون سه هرم برابر با حجم منشور است.پس حجم هرم برابر با این رابطه است.
حجم یک مخروط چون قاعده آن دایره است،به این صورت نوشته می گردد.
در ریاضیات مدرن، این فرمول را می توان به راحتی با استفاده از حساب دیفرانسیل و انتگرال محاسبه کرد - تا مقیاس بندی، انتگرال است.بدون استفاده از حساب دیفرانسیل و انتگرال، فرمول را می توان با مقایسه مخروط با یک هرم و اعمال اصل کاوالیری - به ویژه، مقایسه مخروط با یک هرم مربع راست (مقیاس عمودی)، که یک سوم مکعب را تشکیل می دهد، اثبات کرد. این فرمول را نمیتوان بدون استفاده از چنین استدلالهای بینهایتی اثبات کرد - بر خلاف فرمولهای دو بعدی برای مساحت چند وجهی، اگرچه شبیه به مساحت دایره است - و از این رو قبل از ظهور حساب دیفرانسیل و انتگرال، اثباتهای کمتر دقیقتری را پذیرفتند، با یونانیان باستان از روش استفاده میکردند. فرسودگی . این اساساً محتوای مسئله سوم هیلبرت است - به طور دقیق تر، همه اهرام چند وجهی با قیچی همخوانی ندارند.(می توان آن را به قطعات متناهی تقسیم کرد و به قطعات دیگر مرتب کرد) و بنابراین حجم را نمی توان صرفاً با استفاده از یک آرگومان تجزیه محاسبه کرد
مساحت
[ویرایش]مساحت جانبی یک مخروط بر اساس مساحت هرم برابر با این تساوی است.
rشعاع مخروط وLکمان مخروط است
ارتفاع اصلی مخروط دایره ای راست، فاصله ای از هر نقطه از دایره قاعده آن تا راس از طریق یک قطعه خط در امتداد سطح مخروط است. توسط آن داده می شود، جایی کهrشعاع پایه است وhارتفاع است این را می توان با قضیه فیثاغورث ثابت کرد.
مساحت کل مخروط بر اساس این رابطه نوشته می گردد.
مساحت کل یعنی مساحت قاعده به علاوه مساحت جانبی
محاسبه کمان مخروط و دور مخروط
[ویرایش]اگرrشعاع وhارتفاع باشد.دور و کمان مخروط برابر با این رابطه است.
اگرcدور و Lکمان مخروط باشد،مساحت اینگونه است.
براساس زاویه و ارتفاع راس مساحت مخروط برابر با این رابطه است
فرم معادلات
[ویرایش]سطح یک مخروط را می توان به صورت پارامتربندی کرد
جایی که زاویه تتا برابر باو زاویه اطراف مخروط است و ارتفاع جزئی از اعداد حقیقی باشد یعنیاست.
مخروط دایره ای جامد راست با ارتفاعhو دیافراگم، که محور آن استzمحور مختصات و راس آن مبدا است، به صورت پارامتریک به عنوان توصیف می شود
جایی کهu,t,s محدوه بیش از، به ترتیب در شکل ضمنی ، همان جامد با نابرابری ها تعریف می شود.
جایی که به طور کلی، یک مخروط دایره ای راست با راس در مبدا، محور موازی با بردار d و دیافراگم، توسط معادله برداری ضمنی به دست می آیدجایی که
یا
حجم و مساحت هرم
[ویرایش]حجم
[ویرایش]حجم یک هرم (همچنین هر مخروطی) است، کهS مساحت قاعده و h ارتفاع از قاعده تا راس است. این برای هر چند ضلعی، منتظم یا غیرمنظم، و هر مکان راس کار می کند، مشروط بر اینکه h به عنوان فاصله عمود از صفحه حاوی قاعده اندازه گیری شود.
فرمول را می توان به طور رسمی با استفاده از حساب دیفرانسیل و انتگرال اثبات کرد. با تشابه، ابعاد خطی یک مقطع موازی با پایه به صورت خطی از راس به پایه افزایش می یابد. ضریب مقیاس (ضریب تناسب) است، یا، که در آن h ارتفاع و y فاصله عمود از صفحه پایه تا سطح مقطع است. از آنجایی که مساحت هر مقطع با مربع ضریب پوسته پوسته شدن شکل متناسب است ، مساحت سطح مقطع در ارتفاع y برابر است بایا از آنجایی که b و h یاهر دو ثابت هستند و دو عبارتوداریم. حجم توسط انتگرال داده می شود
همین معادله،همچنین برای مخروط ها با هر پایه نگه می دارد. این را می توان با استدلالی مشابه استدلال فوق اثبات کرد; حجم یک مخروط را ببینید .
به عنوان مثال، حجم هرمی که قاعده آن یک چندضلعی منتظم n ضلعی با طول ضلع s و ارتفاع آن h است.
این فرمول را می توان دقیقاً بدون حساب برای اهرام با پایه های مستطیلی نیز به دست آورد. یک مکعب واحد را در نظر بگیرید. از مرکز مکعب به هر یک از 8 راس خطوط بکشید. این مکعب را به 6 هرم مربع مساوی با سطح پایه 1 و ارتفاع 1/2 تقسیم می کند. حجم هر هرم به وضوح 1/6 است. از این نتیجه می گیریم که حجم هرم =
(3/ارتفاع × مساحت پایه)
در مرحله بعد، مکعب را به طور یکنواخت در سه جهت به مقدار نامساوی باز کنید تا لبه های مستطیلی مستطیل شکل a , b و c با حجم جامد abc باشند. هر یک از 6 هرم داخل نیز به همین ترتیب گسترش یافته اند. و هر هرم دارای همان حجم abc /6 است. از آنجایی که جفت اهرام دارای ارتفاع های a /2، b /2 و c /2 هستند، می بینیم که حجم هرم = ارتفاع × مساحت پایه / 3 دوباره.
وقتی مثلث های ضلعی متساوی الاضلاع باشند، فرمول حجم به این صورت است
این فرمول فقط برای n = 2، 3، 4 و 5 اعمال می شود. و همچنین مورد n = 6 را پوشش می دهد که حجم آن برابر با صفر است (یعنی ارتفاع هرم صفر است).
مساحت
[ویرایش]مساحت یک هرم برابر با این رابطه است.
Pیعنی محیط چندضلعی و Bیعنی مساحت قاعده هرم است.
Lکمان هرم است و فرمول آن بر اساس این رابطه نوشته می گردد
اگر قاعده هرم چندضلعی باشد بر اساس این رابطه نوشته می گردد
anیعنی Pو محیط چندضلعی است.
حجم کره
[ویرایش]حجم کره بر اساس این رابطه نوشته می گردد. در این رابطه، r شعاع کره و π عدد پی است. این رابطه را نخستین بار ارشمیدس بدست آورد. او نشان داد که حجم یک کره ۲/۳ حجم استوانهٔ محیطی آن کرهاست. حجم کره بر اساس این رابطه نوشته می گردد.
اثبات حجم کره
[ویرایش]یک کره را در یک استوانه که قطر و ارتفاع آن برابر است محاط می کنیم. ابتدا کره را به دو نیم کره تقسیم میکنیم. اگر نیم کره را سه بار آب کنیم و در استوانه بریزیم حجم استوانه پر می شود.پس حجم نیمکره یک سوم حجم استوانه است و حجم کره دو سوم حجم استوانه است.

حجم استوانه=
اگر نسبت حجم کره به حجم استوانه را بر حجم استوانه ضرب کنیم حجم کره بدست می آید
که r شعاع و d قطر کره است. ارشمیدس ابتدا این فرمول را با نشان دادن اینکه حجم درون یک کره دو برابر حجم بین کره و استوانه محصور آن کره است (با ارتفاع و قطر برابر با قطر کره) به دست آورد. این را می توان با نوشتن یک مخروط به صورت وارونه در نیمکره ثابت کرد، با توجه به اینکه مساحت مقطع مخروط به اضافه سطح مقطع کره با سطح مقطع کره برابر است. استوانه محدود کننده، و استفاده از اصل کاوالیری . این فرمول همچنین می تواند با استفاده از حساب انتگرال نیز به دست آورد، یعنی ادغام دیسک برای مجموع حجم های بی نهایت از دیسک های دایره ای با ضخامت بی نهایت کوچک که در کنار هم چیده شده اند و در امتداد محور x از x = - r تا x = r متمرکز شده اند ، با فرض اینکه کره شعاع r در مرکز قرار گرفته است. اصل و نسب.
اثبات حجم کره به روش انتگرال ومثلثات
[ویرایش]نخست حجم نیم کره را بدست میآوریم و چون کره متقارن است حجم یک کرهٔ کامل دو برابر حجم نیم کره میشود. فرض کنید این کره از تعداد بی شماری دیسک دایرهای با ضخامت بسیار کم ساخته شدهاست. مجموع (انتگرال) حجم این دیسکها، حجم کرهٔ مورد نظر را میسازد. محور تمام این دیسکها بر روی محور yها قرار دارد در نتیجه دیسکی که بر روی نقطهٔ h = ۰ قرار دارد، شعاعی برابر با r دارد (s = r) و دیسکی که در نقطهٔ h = r قرار دارد، شعاعی برابر با صفر دارد (s = ۰).
اگر ضخامت دیسکها در هر نقطهٔ دلخواه h، برابر با δh باشد، آنگاه حجم دیسک برابر خواهد بود با مساحت مقطع دیسک در ضخامت آن:
پس حجم کل نیم کره برابر است با مجموع حجم دیسکها:
در بالای کره، شعاع دیسکها بسیار کوچک و نزدیک به صفر است. در نتیجه برای بدست آوردن مجموع حجم دیسکها باید از رابطهٔ بالا، انتگرال گرفت:
با توجه به قضیه فیثاغورس میدانیم که در هرنقطه بر روی محور عمودی داریم:
پس به جای از رابطهٔ زیر که تابعی از مقدار است استفاده میکنیم:
مقدار تازهٔ را در انتگرال جایگذاری میکنیم:
مقدار انتگرال برابر است با:
حجم نیمی از کره برابر با است پس حجم کل کره میشود:
حجم کره در دستگاه مختصات قطبی نیز قابل محاسبه است که در آن حالت باید از رابطهٔ زیر استفاده کرد:
بنابر این داریم
برای بیشتر اهداف عملی، حجم داخل یک کره حک شده در یک مکعب را می توان به 52.4٪ حجم مکعب تقریب زد، زیرا V =π/6 d 3 که d قطر کره و همچنین طول یک ضلع مکعب است وπ/6 ≈ 0.5236. به عنوان مثال، کره ای با قطر 1 متر، 52.4 درصد حجم یک مکعب با طول لبه 1 متر یا حدود 0.524 متر مکعب دارد.
بر اساس بازتابی از ریاضیدانان ارشمیدس یونانی، برای نیمکره ای با شعاع میدان مرجعی وجود دارد که حجم آن با نیمکره مطابقت دارد، اما محاسبه آسان است. این بدنه مقایسه با تبدیل یک استوانه (به طور دقیق تر: یک استوانه دایره ای راست) با شعاع سطح پایه و ارتفاع به a مخروط (به طور دقیق تر: مخروط دایره ای راست) با شعاع پایه و ارتفاع حذف شده است. فکر کنم نادرست باشد برای همین ادامه ندادم
می توان از اصل کاوالیری برای اثبات اینکه نیمکره و جسم مقایسه دارای حجم یکسانی هستند استفاده کرد. این اصل مبتنی بر ایده تقسیم اجسام در نظر گرفته شده به برش های بی نهایت با ضخامت بی نهایت کوچک (بی نهایت کوچک) است. (یک جایگزین برای این روش استفاده از حساب انتگرال خواهد بود.) با توجه به اصل ذکر شده، سطوح تقاطع هر دو جسم را با صفحه که موازی و یک فاصله از آن داده شده است. در مورد نیمکره، تقاطع یک ناحیه دایره ای است.
شعاع این ناحیه دایره ای از قضیه فیثاغورث حاصل می شود:
- .
این برای محتوای رابط می دهد
- .
از طرف دیگر، در مورد جسم مرجع، تقاطع یک حلقه دایره ای با شعاع بیرونی و یک شعاع داخلی است. مساحت این تقاطع بنابراین
- .
برای فاصله دلخواه تا ناحیه پایه، دو ناحیه تقاطع در محتوای ناحیه توافق دارند. این از اصل کاوالیری ناشی می شود که نیمکره و بدن مقایسه دارای حجم یکسانی هستند.
اکنون می توان حجم بدن مقایسه و در نتیجه نیمکره را به راحتی محاسبه کرد:
یکی کمتر از حجم استوانه و یکی بیشتر از حجم مخروط.
بنابراین، موارد زیر در مورد حجم کره (جامد) صدق می کند:
- .
اشتقاق جایگزین
[ویرایش]کره را می توان به بی نهایت هرم با ارتفاع (راس در مرکز کره) تقسیم کرد که قاعده کل آنها با سطح کره مطابقت دارد (به زیر مراجعه کنید). بنابراین حجم کل همه اهرام برابر است با:
.
استخراج با استفاده از حساب انتگرال
[ویرایش]شعاع در فاصله :
- .
ناحیه دایره ای در فاصله :
- .
حجم کره:
- .
حجم یک قطعه کروی از ارتفاع را می توان به همین ترتیب محاسبه کرد:
- .
مشتقات بیشتر
[ویرایش]کره ای با شعاع که مرکز آن در مبدا مختصات است، می تواند با معادله نمایش داده شود:
توضیح داده می شود که در آن مختصات فاصله هستند.
این مشکل را می توان به دو روش با استفاده از حساب انتگرال حل کرد:
ما کره را به یک مجموعه تهی لبسگو پارامتر بندی می کنیم.
با تعیین عملکردی:
عنصر حجم مورد نیاز به عنوان نتیجه میشود:
- .
بنابراین حجم کره به این صورت داده می شود:
امکان دیگر از طریق مختصات قطبی است:
اکنون دستگاه مختصات دکارتی به سیستم مختصات قطبی تبدیل می شود، به این معنی که ادغام پس از تغییر سیستم مختصات با استفاده از متغیرهای و به جای و . انگیزه این تحول، ساده سازی قابل توجه محاسبه در دوره بعدی است. برای دیفرانسیل این به این معنی است:
راه دیگر با کمک فرمول بدنه های انقلاب:
اگر قطعه ای از سطح را حول یک محور مکانی ثابت بچرخانید، جسمی با حجم معین به دست می آورید. در مورد یک ناحیه دایره ای، یک کره تشکیل می شود. این را می توان به عنوان یک سکه در حال چرخش تجسم کرد.
فرمول کلی برای چرخش بدن انقلاب حول محور x به دست میدهد:
- .
معادله به صورت دایره ای است:
با مرکز:
- .
با وصل کردن معادله دایره، دریافت می کنیم"
- .
با جایگزین کردن فرمول بدنه های چرخشی حول محور x، دریافت می کنیم:
مساحت کره
[ویرایش]مساحت کره از رابطهٔ زیر بدست میآید:
ارشمیدس نخستین کسی بود که توانست مساحت کره را بدست آورد. مشتق حجم کره نسبت به r، شعاع کره، مساحت کره را بدست میدهد. میتوان این گونه تصور کرد که حجم یک کره برابر است با مجموع مساحتهای بیشمار پوستهٔ کروی با ضخامت ناچیز که شعاع آنها از ۰ تا r میتواند متفاوت باشد. در نتیجه اگر هریک از جزء حجمهای کره را با δV، ضخامت هر پوسته را با δr و مساحت هر پوستهٔ کروی با شعاع r با(A(rنمایش دهیم؛ رابطهٔ زیر میان این متغیرها برقرار خواهد بود:
حجم کل برابر است با مجموع حجم هریک از این پوستهها:
هنگامی که δr به سمت صفر میل میکند باید از انتگرال بجای سیگما استفاده کنیم:
چون قبلاً فرمول حجم کره را بدست آوردهایم، پس خواهیم داشت:
از دو سر رابطهٔ بالا مشتق میگیریم:
که در حالت عمومی به صورت زیر نوشته میشود:
در دستگاه مختصات قطبی جزء سطح به صورت و در دستگاه مختصات دکارتی به صورت بدست میآید.
مساحت کل کره از انتگرال جزء سطح در تمام سطح کره بدست میآید:
کره دارای کمترین سطح در بین تمام سطوحی است که حجم معینی را در بر می گیرند و بیشترین حجم را در بین تمام سطوح بسته با یک سطح معین در بر می گیرد. بنابراین کره در طبیعت ظاهر می شود: برای مثال، حباب ها و قطرات کوچک آب تقریباً کروی هستند زیرا کشش سطحی به طور محلی سطح سطح را به حداقل می رساند.
مساحت سطح نسبت به جرم یک توپ را مساحت سطح مخصوص می نامند و می توان آن را از معادلات ذکر شده در بالا به صورت بیان کرد.
که ρ چگالی ( نسبت جرم به حجم) است.
روش دیگر
[ویرایش]سطح کره، سطح دو بعدی است که لبه کره را تشکیل می دهد. بنابراین مجموعه تمام نقاطی است که فاصله آنها از مرکز کره دارای مقدار ثابت است. این یک منیفولد دو بعدی بسته است. مساحت آن را همانطور که گفتیم برابر با است که این یعنی چهار برابر با مساحت دایره و دو سوم و همان مساحت سطح استوانه دایرهای است که کره را در بر می گیرد.برای یک حجم معین، کره کوچکترین سطح را در بین تمام اجسام ممکن دارد.
محاسبه مساحت
[ویرایش]
اگر یک کره را به زیر تقسیم کنید:
- لایه های هر کدام با ارتفاع باشد.
- طولی که در خط استوا نیز از هم فاصله دارند.
و اجازه دهید برای تلاش کند،
- بنابراین طول هر سلول برعکس متناسب با است—یعنی با فاصله آن از محور مرکزی.
- این از تصویر بالا در سمت راست مشخص است: فاصله نقطه مماس تا محور مرکزی است. مماس بر "سخن" عمود است و دو مثلث (راست) مشابه هستند. بر این اساس:
- .
- با این حال، عرض هر فیلد با متناسب است.
- این به طور مستقیم از نقاشی زیر، "نمای بالا" دنبال می شود.
بنابراین طول ضرب در عرض همیشه یکسان است، یعنی. همه میدان های مربع مساحت یکسانی دارند.
مساحت خط استوا است ( که در آن به تمایل دارد زیرا در خط استوا به سریعتر از به تمایل دارد. از آنجایی که همه فیلدها دارای محتوای هستند و در مجموع (تعداد فیلدها در جهت افقی ضربدر تعداد فیلدها در جهت عمودی، به عنوان مثال) وجود دارد در آنجا فیلد میشود مساحت کل همه فیلدها است: .
مشتق جایگزین با استفاده از حجم کره
[ویرایش]کره ای را می توان متشکل از بی نهایت بی نهایت کوچک (بی نهایت کوچک) هرم تصور کرد. پایه های این اهرام با هم سطح کره را تشکیل می دهند. ارتفاع اهرام برابر با شعاع کره است. از آنجایی که حجم هرم با فرمول داده میشود، یک رابطه متناظر با حجم کل همه هرمها، یعنی حجم کره اعمال میشود:
- (
بر اساس پیدا کردن حجم کره به صورت مساحت کره برابر با:
مشتق جایگزین با استفاده از حجم یک کره و حساب دیفرانسیل
[ویرایش]حجم کره بر اساس این فرمولتعریف میشود و از سوی دیگر، سطح با توجه به تغییر حجم تعریف می شود:
این است که فرمول سطح بلافاصله از مشتق فرمول حجم پیروی می کند.
استخراج با استفاده از حساب انتگرال
[ویرایش]به صورت انتگرالی اینگونه بدست می آید
برای سطح جانبی بدنه چرخشی:
استخراج با استفاده از حساب انتگرال در مختصات کروی
[ویرایش]برای عنصر سطح روی سطوح = ثابت در مختصات کروی اعمال می شود:
- .
این امر محاسبه سطح را آسان می کند:
نسبتSA:V احجام هندسی
[ویرایش]نسبت مساحت سطح به حجم یا نسبت سطح به حجم که با علائم مختلفی مثل sa/vol و SA:V نشان داده میشود؛ عبارت است از مقدار مساحت سطح در واحد حجم یک شی یا مجموعهای از اشیا. در واکنشهای شیمیایی که یک ماده جامد درگیر باشد، نسبت سطح به حجم یک عامل مهم است که نشان میدهد واکنشهای شیمیایی در حال انجام است.نسبت سطح به حجم یاSA:V یک فرمولی است که از نسبت حجم به سطح کل است و مقادیر آن در احجام هندسی متفاوت است. نسبتSA:Vبه اندازه شعاع یا اندازه احجام هندسی بستگی دارد.
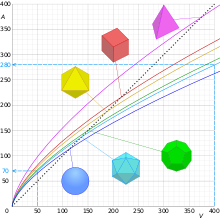
نسبت V/Sاجسام هندسی
[ویرایش]نسبتV/Sمکعب:
نسبتV/Sچهاروجهی:
نسبت V/Sمنشور:
نسبتV/Sاستوانه:
نسبتV/Sهرم:
نسبتV/Sمخروط:
نسبتV/Sکره=
SA:V برای توپهای معمولی و Nبعدی
[ویرایش]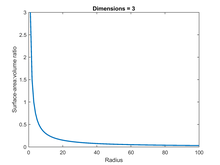
توپ یک شیء سه بعدی به شکل کره است (دراین مبحث بیشتر ناحیه (مساحت) روی کره مورد نظر است نه حجم داخل آن). توپها در هر چند بعد که نیاز باشد میتوانند وجود داشته باشند و در حالت کلی توپ n بعدی نامیده میشوند که n تعداد ابعاد توپ است. برای یک توپ معمولی سه بعدی میتوان SA:V را با استفاده از معادله استاندارد مساحت و حجم حساب کرد؛ که در آن مساحت و حجم است. برای توپی به شعاع واحد (r=۱) نسبت سطح به حجم برابر با ۳ میشود. SA:V با شعاع رابطه عکس دارد، اگر شعاع ۲ برابر شود SA:V نصف میشود.
استدلال بالا را میتوان برای توپ n بعدی تعمیم داد و روابط کلی حجم و مساحت رویه را به شکل زیر نوشت:
حجم؛ مساحت سطحی
نسبت در حالت n بعدی به کاهش پیدا میکند؛ بنابراین همان رابطهٔ خطی برای سطح و حجم در هر بعد برقرار است: دو برابر کردن شعاع همواره نسبت را نصف میکند.
دوران اشکال هندسی
[ویرایش]از دوران یک مستطیل حول یکی از اضلاعش= استوانه
از دوران یک مثلث قائمالزاویه حول یکی از اضلاع مجاورش= مخروط
از دوران یک ذوزنقه قائم الزاویه حول ضلع قائم= مخروط ناقص
از دوران یک مثلث قائم الزاویه حول وتر= دو مخروط
از دوران یک دایره حول قطر به اندازه○180= کره
از دوران یک نیم دایره حول قطر به اندازه○360= کره
در دوران حجم آن ضلعی که حول شکل آن دوران می دهد بچرخد ارتفاع میشود اما آن ضلعی که چرخیده می شود شعاع آن جسم است.

ترسیم سه نما
[ویرایش]
ترسیم سه نما به ترسیمی در هندسه می گویند که نمای جسم سه بعدی را رسم می کند که این مبحث جهات بالا،پایین،راست،چپ،روبه رو و پشت را به سه نمای بالا،راست،روبه رو خلاصه می کند.اگر نمایی از چپ،پایین،پشت با نمای راست،بالا،روبه رو مطابقت نکرد آن را با خط چین مشخص می کنیم.ترسیم سه نما در معماری و ترسیم مهندسی به کار برده می شود.البته اجسامی مثل استوانه،مخروط فقط دونما رسم می شود چون نمای روبه رو با راست آنها باهم برابر است کلی بالا آنها باهم فرق دارد اما کره فقط یک نمای آن رسم می شوو چون سه نمای آن باهم هم شکل است.
ترسیم گسترده
[ویرایش]ترسیم به ترسمی گفته می شود که اجزای یک جسم سه بعدی را تجزیه می کند.ترسیم کشیدن گسترده یک جسم هندسی سه بعدی منشوروهرم،استوانه،چندوجهی،مخروط ساده است.منشور وجه های آن به همراه دو قاعده چندضلعی او کشیده میشود و هرن وجه های مثلث به همراه قاعده چندضلعی آو کشیده میشود.استوانه قسمت مستطیلی که دور دایره کشیده شده به همراه دوقاعده دایره کشیده میشود و در هرم قسمت از یک دایره کشیده میشود و چندوجهی وجه های چندضلعی منتظم او کشیده میشود.اما کره به صورت آنالیز و تجزیه آن گسترده آن بدست می آید،ما کره را بدون هیچ کاری آن را به چهار دایره بر اساس قاعده دورن آن را بدست می آوریم که به چهار دایره تقسیم می شود.

مقطع
[ویرایش]مقطع یک نوع مبحث گفته می شود که جسم سه بعدی را از طریق اقفی و عمودی و صاف و مورب قطع می کند و جسم جدید با قاعده جدید درست می کند.از طریق مورب و عمودی شکل حاصل با قاعده فرق دارد و در صاف و افقی شکل حاصل با قاعده فرق ندارد.مشهورترین مقطع،مقطع مخروطی است.

سطح مقطع
[ویرایش]سطح مقطع مساحت قاعده و شکل حاصل از مقطع را محاسبه و آنالیز می کند. بیشترین سطح مقطع کره و هرم و چندوجهی قاعده های آنها است و سطح مقطع در حجم های هندسی با مساحت قاعده آنها برابر است.

نسبت سطح مقطع
[ویرایش]نسبت سطح مقطع یعنی نسبت مساحت قاعده مقطع و مساحت قاعده حجم هندسی است.
در احجام منشوری نسبت سطح مقطع های موازی برابر با یک می شود،چون مقطع های آنها باهم هم مساحت است. در هرم و کره نسبت سطح مقطع ها باهم متفات است.
محاط
[ویرایش]محاط کردن یعنی حجمی را در حجمی احاطه کنیم به شرط آنکه در تمام آن قسمت حجم محاطی در تمام حجم محیطی شعاع آن با آن مماس شود و شعاع و ارتفاع حجم محاطی با شعاع و ارتفاع حجم محیطی برابر باشد.محاطی کره در استوانه یکی از محاط کردن است. کره جسم محاطی است و استوانه جسم محیطی است. با محاط کردن می توان حجم و مساحت احجام را بدست آورد.و نسبت آنهارا بدست آورد

محاطکردن کره در استوانه
[ویرایش]یک کره را در یک استوانه که قطر و ارتفاع آن برابر است محاط می کنیم.به طوری که شعاع کره با شعاع استوانه برابر است و قطر کره بر ارتفاع و قطر استوانه برابر است و شعاع کره نیز بر تمامی نقاط استوانه مماس است.
دراین حالت می گوییم
جسم محاطی:کره
جسم محیطی:استوانه
محاسبه حجم کره
ابتدا کره را به دو نیم کره تقسیم میکنیم. اگر نیم کره را سه بار آب کنیم و در استوانه بریزیم حجم استوانه پر می شود.پس حجم نیمکره یک سوم حجم استوانه است و حجم کره دو سوم حجم استوانه است.
حجم استوانه: اگر نسبت حجم کره به حجم استوانه را بر حجم استوانه ضرب کنیم حجم کره بدست می آید
محاطکردن مخروط در استوانه
[ویرایش]ابتدامخروط را در استوانهای باارتفاعوشعاعمختلف محاطمیکنیم.ارتفاعوشعاعمخروط با ارتفاعوشعاعاستوانه برابر است.درایننوع محاط کردن ارتفاع مخروط بر قاعده استوانه مماسمیگردد.
دراین حالت میگوییم
- جسممحاطی:مخروط
- جسممحیطی:استوانه
محاسبه حجم مخروط
اگرمخروط را فشردهکنیم وبهاستوانه تبدیلکنیم٬یکاستوانه کوچک بهوجود میآید.اگر سهتا ازاین استوانههای فشردهکه قبلامخروط بودند را در استوانهبزرگ جای دهیم.حجماستوانه کامل پرمیشود.
حجماستوانه:
اگر نسبتحجممخروط را بهحجماستوانه را در حجماستوانه ضربکنیم،حجم مخروط بدست میآید
کاربرد
[ویرایش]کاربرد سطح و حجم بیشتر در معماری،نجوم و... استفاده می شود و یکی از مهم ترین عناصر در ریاضیات و هندسه است.مساحت و حجم هم در مبحث هایی چون مختصات کروی و مختصات استوانه ای،مقطعمخروطی،مثلثات کروی،انتگرال و... استفاده میشود.
نگارخانه
[ویرایش]



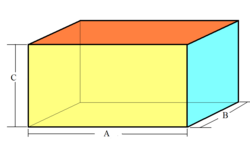










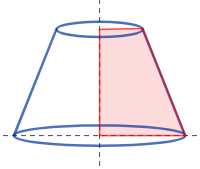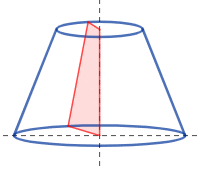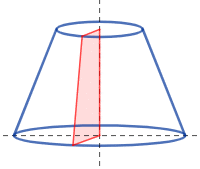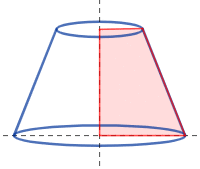
یادداشت
[ویرایش]- Vیعنی نماد حجم(Volume)
- S,Aیعنی نماد مساحت(Area,surface)
- P,pیعنی نماد محیط(periphery)
- aیعنی ضلع مکعب،منشور چندپهلو و چهاروجهی
- a,b,cاضلاع مستطیل و متوازی السطوح
- h,Hیعنی ارتفاع(Height)
- مماس یعنی خطی که بر یک خط در تماس باشد و زاویه تماس آن قائم یا 90درجه باشد،مماس در فضایی سه بعدی باعث محاطی یک جسم می گردد
- برای محاط کردن باید جسم را درجسم دیگر بر حالت مماس احاطه کنیم.
- ترسیم سه نما از سه جهت بالا،روبه رو،راست را میکشیم
- در گسترده کشیدن باید اجزای جسم را بکشیم و بعد آن را درهم طتبیق کنیم
- در مقطع کار اصلی ایجاد قاعده و جسمی جدید است
- سطح مقطع یعنی مساحت حاصل مقطع
- دوران یعنی چرخش
- nیعنی هم تعداد وجه ها و ضلع ها
- 'nیعنی تعداد ضلع های وجه ها
- کره نوعی چندوجهی است که وجه های بی نهایت دارد
- متوازی السطوح،مکعب،مکعب مستطیل از بردار های سه بعدی تشکیل شده اند
- نسبتSA/Vیعنی نسبت حجم به مساحت
- Kرابطه مثلثاتی است. حجم متوازی السطوح از جذر این عدد در کنارضربa,b,c نوشته می شودو از رابطه زیر نوشته می گردد
منابع
[ویرایش]- ویکی پدیای انگلیسی و فارسی(مساحت،حجم)
- ریاضی پایه هفتم و نهم(ترسیم سه نما،محاط،دوران ساده،گسترده کشیدن)
- هندسه پایه دهم و دوازدهم(مقطع،دوران پیشرفته،مختصات سه بعدی،فضایR^3)
- ویکی انبار[۷]
- درسنامه فرادرس[۴]
- مترجم گوگل[۴]
چندضلعی منتظم
چندضلعی منتظم،در هندسه اقلیدوسی چندضلعی است که همه زوایا و اضلاع آن هماندازهاند.چندضلعیهای منتظم، میتوانند کوژ یا به شکل ستاره باشند. در حالت حدی، یک دنباله از چندضلعیهای منتظم با افزایش تعداد اضلاع، در صورت ثابت ماندن محیط به دایره تبدیل میشود و در صورت ثابت ماندن طول ضلع، به apeirogon تبدیل میشود.
محیط و مساحت
[ویرایش]محیط
[ویرایش]محیط چندضلعی منتظم براساس ضرب تعداد ضلع های چندضلعی منتظم و اندازه اضلاع چندضلعی منتظم است.
محیط مساحت براساس این رابطه بدست می آید.دراینجاnبرابر با تعداد اضلاع چندضلعی منتظم است و aدر اینجا برابر با اندازه اضلاع چندضلعس منتظم است.
مساحت
[ویرایش]مساحت چندضلعی منتظم براساس روابط مثلثاتی بدست می آید.مساحت چندضلعی منتظم براساس اینکه از مربع های 1×1ساخته شده است و تعداد اضلاع آنn-تا است و چون براساس عدد پی نیز تعداد اضلاع آن گسترش می یابد به صورت مثلثاتی براساس کتانژانت به صورت عددپی بر تقسیم تعداد اضلاع چندضلعی منتظم بدست می آید.
مساحت چندضلعی منتظم براین اساس نوشته می گردد
دراینجا عدد پی،برحسب رادیان است.(برابربا°۱۸۰)
رابطه مساحت مربع به روش مثلثاتی
[ویرایش]مربع چون یک چندضلعی منتظم است،مساحت آن را می توان به صورت مساحت چندضلعی منتظم که به روش مثلثاتی بدست می آید نیز نوشت که به رابطه به این صورت است:در اینجا:
پس مساحت مربع همراوه با مجذور ضلع آن برابر است.
سایر فرمول های دیگر مساحت
[ویرایش]مساحت یک n-ضلعی منتظم کوژ با اندازهٔ ضلع a، شعاع دایره محیطی R، شعاع دایره محاطی r و محیط p با استفاده از روابط زیر بدست میآید:
(زوایا برحسب رادیان است.)
که در آن R برابر است با:
تعداد قطرها
[ویرایش]برای n > ۲، تعداد قطرهای n-ضلعی، برابر است با ، بهعنوان مثال برای مثلث، چهارضلعی، پنجضلعی و ششضلعی، تعداد قطرها بهترتیب، ۰، ۲، ۵ و ۹ است.
برای یک n-ضلعی منتظم محاطشده در یک دایره به شعاع واحد، حاصلضرب فاصلهٔ هر رأس تا همهٔ رأسهای دیگر، برابر است با n.
زوایا
[ویرایش]زاویه داخلی
[ویرایش]یک nضلعی منتظم را درنظر بگیرید. ابتدا تعداد مثلث هایش را طبق چندضلعی های معروف محاسبه میکنیم
- مربع:۲مثلث
- پنج ضلعی منتظم:۳مثلث
- شش ضلعی منتظم:۴مثلث
- هفت ضلعی منتظم:۵مثلث
- هشت ضلعی منتظم:۶مثلث
- نه ضلعی منتظم:۷مثلث
- ده ضلعی منتظم:۸مثلث
چون مجموعه زاویههایی داخلی یک مثلث°۱۸۰درجه است پس مجموعه زاویههایی داخلی بر اساس مجموع زاویه های تعداد مثلث های دورن او است.تعداد مثلث:
اندازه زاویهداخلی چندضلعی منتظم برابر با تقسیم تعداد ضلعها است.چون تعداد راس ها با تعداد ضلعها برابر است.مجموع زاویه داخلی:
اندازه زاویهداخلی:
زاویه خارجی
[ویرایش]مجموع زاویه خارجی:360درجه اندازه زاویه خارجی:
ویژگی
[ویرایش]ویژگیهای بیانشده در ادامه، برای همهٔ چندضلعیهای منتظم (اعم از کوژ و ستارهای) برقرار است.
یک چندضلعی منتظم n-ضلعی، تقارن چرخشی از مرتبهٔ n دارد.
همهٔ رأسهای یک چندضلعی منتظم بر روی یک دایره (دایره محیطی) قرار میگیرند. بهعبارت دیگر، رأسها نقاطی همدایره هستند. یعنی یک چندضلعی منتظم، لزوماً یک چندضلعی دایرهای هم هست.
هر چندضلعی منتظم، یک دایره محاطی دارد که به همه اضلاع در نقطهٔ وسط آنها مماس است. بنابراین هر چندضلعی منتظم، لزوماً یک چندضلعی مماسی هم هست.
یک n-ضلعی منتظم با استفاده از خطکش و پرگار قابل ترسیم است؛ اگر و تنها اگر فاکتورهای اول فرد n، اعداد اول فرمای متفاوتی باشند.
چندضلعی های منتظم محیطی، بیشترین مساحت را در دایره دارند. به عنوان مثال بین همهی سه ضلعی های محیطی در یک دایره مثلث متساوی الاضلاع و در بین همه ی چهار ضلعی های محیطی در یک دایره مربع بیشترین مساحت را دارد.
منابع
[ویرایش]ویکی پدیای فارسی
زاویه داخلی و خارجی
هندسه ریمانی
هندسه ریمانی، شاخهای از هندسه دیفرانسیل است که به مطالعه منیفلدهای ریمانی می پردازد، یعنی منیفلدهای هموار مجهز به متریک ریمانی، این ساختار منیفلد را در هر نقطه مجهز به ضرب داخلی روی فضای مماس می کند، به طوری که از نقطهای به نقطه دیگر به طور هموار تغییر میکند. همچنین این ساختار به طور خاص مفاهیم موضعی چون زاویه، طول خم، مساحت رویه و حجم را بدست می دهد. از اینها، برخی از سایر کمیّتهای سرتاسری را می توان به وسیله انتگرالگیری بدست آورد.
هندسه ریمانی، از بینش برنهارت ریمان نشأت گرفت که در نطق افتتاحیه خودش (با عنوان «در مورد فرضیاتی که هندسه بر آن بنا نهاده شده») آن را بیان داشت. این هندسه، تعمیم بسیار وسیع و مجردی از هندسه دیفرانسیل رویههای درون است. توسعه هندسه ریمانی منجر به ایجاد نتایج متنوعی در ارتباط با هندسه رویهها و رفتار ژئودزیک رویشان شد، به همراه تکنیکهایی که می توان از آن ها در مطالعه منیفلدهای دیفرانسیلپذیر ابعاد بالاتر استفاده کرد. این ساختار منجر به فرموله کردن نسبیت عام انشتین شده و اثرات ژرفی را بر روی نظریه گروهها، نظریه نمایش، و آنالیز ایجاد کرده و موجب توسعه توپولوژی جبری و توپولوژی دیفرانسیل گشته است.
مقدمه
[ویرایش]هندسه ریمانی اولین بار به طور کلی توسط برنهارد ریمان در قرن نوزدهم مطرح شد. با طیف وسیعی از هندسهها سروکار دارد که ویژگیهای متریک آنها از نقطهای به نقطه دیگر متفاوت است، از جمله انواع استاندارد هندسه غیراقلیدسی .
هر منیفولد صاف یک متریک ریمانی را می پذیرد که اغلب به حل مسائل توپولوژی دیفرانسیل کمک می کند . همچنین به عنوان سطح ورودی برای ساختار پیچیدهتر منیفولدهای شبه ریمانی ، که (در چهار بعد) اشیاء اصلی نظریه نسبیت عام هستند، عمل میکند. از دیگر تعمیم هندسه ریمانی می توان به هندسه فینسلر اشاره کرد.
تشابه نزدیکی از هندسه دیفرانسیل با ساختار ریاضی عیوب در بلورهای منظم وجود دارد. دررفتگی ها و بریدگی ها باعث ایجاد پیچش و انحنا می شوند.
قضایا
[ویرایش]مقده ای از قضایای کلی
[ویرایش]آنچه در زیر می آید فهرست ناقصی از کلاسیک ترین قضایا در هندسه ریمانی است. انتخاب بسته به اهمیت و ظرافت فرمولاسیون آن انجام می شود. بیشتر نتایج را می توان در تک نگاری کلاسیک جف چیگر و دی. ایبین یافت (به زیر مراجعه کنید). فرمول های ارائه شده بسیار دقیق یا کلی نیستند. این فهرست برای کسانی است که از قبل تعاریف اولیه را میدانند و میخواهند بدانند این تعاریف در مورد چیست.
قضایای عمومیویرایش کنید
[ویرایش]- قضیه گاوس-بونه انتگرال انحنای گاوس روی منیفولد ریمانی فشرده 2 بعدی برابر است با 2πχ( M ) که در آن χ( M ) مشخصه اویلر M را. این قضیه یک تعمیم به هر چندبعدی فشرده ریمانی دارد، به قضیه تعمیم یافته گاوس-بونت مراجعه کنید.
- قضایای جاسازی نش آنها بیان می کنند که هر منیفولد ریمانی را می توان به صورت ایزومتریکدر فضای اقلیدسی R n جاسازی کرد .
هندسه در بزرگویرایش کنید
[ویرایش]در تمام قضایای زیر، برخی از رفتارهای محلی فضا (معمولاً با استفاده از فرض انحنای فرمولبندی میشوند) را برای به دست آوردن اطلاعاتی در مورد ساختار کلی فضا، از جمله برخی اطلاعات در مورد نوع توپولوژیکی منیفولد یا رفتار نقاط، فرض میکنیم. در فواصل "به اندازه کافی بزرگ".
انحنای مقطعی فشردهویرایش کنید
[ویرایش]- قضیه کره . اگر M یکمنیفولد ریمانی n بعدی فشرده با انحنای مقطعی باشد که کاملاً بین 1/4 و 1 فشرده شده باشد، M به یک کره دیفئومورفیک است.
- قضیه تناهی چیگر. با توجه به ثابت های C ، D و V ، منیفولدهای ریمانی فشرده n بعدی با انحنای مقطعی به تعداد محدود (تا دیفئومورفیسم) وجود دارد. K | ≤ C ، قطر ≤ D و حجم ≥ V.
- منیفولدهای تقریباً مسطح گروموف . یک ε n > 0 وجود دارد به طوری که اگر یکمنیفولد ریمانی n بعدی دارای یک متریک با انحنای مقطعی باشد | K | ≤ ε n و قطر ≤ 1 پس پوشش محدود آن به منیفولد صفر دیفرومورفیک است .
انحنای مقطعی در زیر محدود شده استویرایش کنید
[ویرایش]- قضیه روح چیگر-گرومول . اگر M یک منیفولد ریمانی n- بعدی منحنی کامل غیر فشرده و غیر فشرده باشد، آنگاه M حاوی یک زیرمنیفولد S فشرده و کاملاً ژئودزیکی است به طوری که M نسبت به بسته نرمال S متمایز است ( S روح M نامیده می شود ) . به ویژه، اگر M در همه جا انحنای کاملاً مثبت داشته باشد، آنگاه با Rn تفاوت دارد . G. Perelman در سال 1994 یک مدرک شگفتانگیز زیبا/کوتاه از حدس روح ارائه کرد:اگر فقط در یک نقطه دارای انحنای مثبت باشد، M نسبت به Rn دیفئومورفیک است.
- قضیه اعداد بتی گروموف. یک ثابت C = C ( n ) وجود دارد به طوری که اگر M یک منیفولد ریمانی n بعدی متصل فشرده با انحنای مقطعی مثبت باشد، مجموع اعداد بتی آن حداکثر C است.
- قضیه تناهی گرو-پترسن. با توجه به ثابتهای C ، D و V ، تعداد محدودی از انواع همتوپی از منیفولدهای ریمانی فشرده n بعدی با انحنای مقطعی K ≥ C ، قطر ≤ D و حجم ≥ V وجود دارد.
انحنای مقطع در بالا محدود شده استویرایش کنید
[ویرایش]- قضیه Cartan - Hadamard بیان میکند که یک منیفولد ریمانی کاملاً متصل به سادگی با انحنای مقطعی غیر مثبت با فضای اقلیدسی Rn با n = dim M از طریق نقشه نمایی در هر نقطه تفاوت دارد. این نشان می دهد که هر دو نقطه از یک منیفولد ریمانی کامل متصل به سادگی با انحنای مقطعی غیر مثبت توسط یک ژئودزیک منحصر به فرد به هم می پیوندند.
- جریان ژئودزیکی هر منیفولد فشرده ریمانی با انحنای مقطعی منفی ارگودیک است .
- اگر M یک منیفولد ریمانی کامل با انحنای مقطعی است که در بالا با یک ثابت کاملاً منفی k محدود شده است، یک فضای CAT( k ) است . در نتیجه، گروه بنیادی آن Γ = π 1 ( M ) گروموف هذلولی است . این پیامدهای زیادی برای ساختار گروه بنیادی دارد:
- به طور محدود ارائه شده است .
- کلمه مشکل برای Γ یک راه حل مثبت دارد.
- گروه Γ دارای ابعاد همولوژیکی مجازی محدودی است .
- فقط شامل تعداد محدودی از کلاسهای مزدوج از عناصر با نظم محدود است .
- زیرگروه های آبلی Γ تقریباً حلقوی هستند ، به طوری که دارای زیرگروه ایزومورف به Z × Z نیست.
انحنای ریچی در زیر محدود شده استویرایش کنید
[ویرایش]- قضیه مایرز اگر یک منیفولد ریمانی کامل دارای انحنای ریچی مثبت باشد، گروه بنیادی آن محدود است.
- فرمول بوشنر اگر یک منیفولد n فشرده ریمانی دارای انحنای ریچی غیرمنفی باشد، اولین عدد بتی آن حداکثر n است، اگر و فقط اگر منیفولد ریمانی یک چنبره مسطح باشد برابر است.
- قضیه تقسیم . اگر یک منیفولد ریمانی n بعدی دارای انحنای ریمانی غیرمنفی و یک خط مستقیم باشد (یعنی ژئودزیکی که فاصله را در هر بازه به حداقل میرساند) آنگاه به یک ضرب مستقیم خط واقعی و یکریمانی کامل ( n -1) بعدی ایزومتریک است. منیفولدی که دارای انحنای ریچی غیرمنفی است.
- نابرابری اسقف - گروموف حجم یک توپ متریک شعاع r در یک منیفولد ریمانی کامل n بعدی با انحنای ریچی مثبت حداکثر حجم توپی با همان شعاع r در فضای اقلیدسی است.
- قضیه فشردگی گروموف . مجموعه تمام منیفولدهای ریمانی با انحنای ریچی مثبت و حداکثر قطر D در متریک گروموف-هاسدورف از پیش فشرده است .
انحنای ریچی منفیویرایش کنید
[ویرایش]- را ایزومتری یک منیفولد فشرده ریمانی با انحنای ریچی منفی گسسته است .
- هر منیفولد صاف با بعد n ≥ 3 یک متریک ریمانی با انحنای ریچی منفی را تایید می کند. ( این برای سطوح صادق نیست .)
انحنای اسکالر مثبتویرایش کنید
[ویرایش]- راچنبره بعدی n اسکالر مثبت را نمی پذیرد.
- اگر شعاع تزریق یک منیفولد ریمانی n بعدی فشرده ≥ π باشد، میانگین انحنای اسکالر حداکثر n ( n -1) است.
منابع
[ویرایش]https://en.m.wikipedia.org/wiki/Riemannian_geometry
هندسه تصویری
هندسهی تصویری (به انگلیسی: Projective Geometry) شاخهای از دانش هندسه است که به مطالعه خواص هندسیای میپردازد که در تبدیلهای تصویری ثابت می مانند. بارزترین تفاوت این هندسه با هندسهی فضای شهودی یا هندسهی اقلیدسی در حذفشدنِ اصل توازیست. در هندسه تصویری، در هر بعد، فضای تصویری نقاط بیشتری از فضای اقلیدسی دارد و بعلاوه تبدیلهای هندسی که این نقاط (که به نام نقاط در بینهایت خوانده میشوند) را به نقاط معمولی و بالعکس منتقل میکند، مجاز هستند.
هندسه تصویری شکلی پایهای و غیر متریک از هندسه است، یعنی برپایه مفهوم فاصله بنا نشده است. این هندسه در فضای دو بعدی با مطالعه پیکربندیهای نقاط و خطوط آغاز میشود.
ویژگی های معنادار
[ویرایش]ویژگیهای معنادار برای هندسه تصویری توسط این ایده جدید تبدیل، که در تأثیرات آن رادیکالتر از آن چیزی است که با یک ماتریس تبدیل و ترجمهها ( تبدیلهای وابسته ) بیان شود، احترام گذاشته میشود. اولین مسئله برای هندسهسنجها این است که چه نوع هندسهای برای یک موقعیت جدید مناسب است. ارجاع به زوایا در هندسه تصویری مانند هندسه اقلیدسی امکان پذیر نیست ، زیرا زاویه نمونه ای از مفهومی است که نسبت به تبدیل های تصویری ثابت نیست، همانطور که در ترسیم پرسپکتیو مشاهده می شود . یک منبع برای هندسه تصویری در واقع نظریه پرسپکتیو بود. تفاوت دیگر با هندسه ابتدایی روشی است که در آن وجود داردمی توان گفت که خطوط موازی در نقطه ای در بی نهایت به هم می رسند ، زمانی که مفهوم به اصطلاحات هندسه تصویری ترجمه شود. مجدداً این مفهوم دارای یک مبنای شهودی است، مانند برخورد خطوط راه آهن در افق در یک ترسیم پرسپکتیو. برای اطلاع از مبانی هندسه تصویری در دو بعدی به صفحه تصویری مراجعه کنید .
ایده ها
[ویرایش]در حالی که این ایده ها قبلاً در دسترس بودند، هندسه تصویری عمدتاً توسعه قرن نوزدهم بود. این شامل نظریه فضای تصویری پیچیده بود، مختصات استفاده شده ( مختصات همگن ) اعداد مختلط هستند. چندین نوع اصلی از ریاضیات انتزاعی تر (از جمله نظریه ثابت ، مکتب هندسه جبری ایتالیایی ، و برنامه ارلانگن فلیکس کلاین که منجر به مطالعه گروه های کلاسیک می شود ) توسط هندسه تصویری انگیزه داده شدند. همچنین به عنوان هندسه مصنوعی ، موضوعی با تمرینکنندگان زیادی بود . موضوع دیگری که از مطالعات بدیهی هندسه تصویری ایجاد شده استهندسه محدود .
مباحث
[ویرایش]مبحث هندسه تصویری در حال حاضر خود به بسیاری از موضوعات فرعی تحقیقاتی تقسیم می شود که دو نمونه از آنها هندسه جبری تصویری (مطالعه انواع تصویری ) و هندسه دیفرانسیل تصویری (مطالعه متغیرهای دیفرانسیل تبدیل های تصویری) است.
بررسی ها
[ویرایش]هندسه فرافکنی یک شکل غیر متریک ابتدایی هندسه است، به این معنی که بر مفهوم فاصله استوار نیست. در دو بعد با مطالعه پیکربندی نقاط و خطوط آغاز می شود . این که واقعاً مقداری علاقه هندسی در این محیط پراکنده وجود دارد، ابتدا توسط دسارگو و دیگران در کاوش در اصول هنر پرسپکتیو مشخص شد. در فضاهای با ابعاد بالاتر ، ابرصفحه ها (که همیشه به هم می رسند) و سایر فضاهای فرعی خطی در نظر گرفته می شوند که اصل دوگانگی را نشان می دهند.. ساده ترین تصویر دوگانگی در صفحه نمایشی است، جایی که گزاره های "دو نقطه متمایز یک خط منحصر به فرد را تعیین می کنند" (یعنی خطی که از آنها عبور می کند) و "دو خط مجزا یک نقطه منحصر به فرد را تعیین می کنند" (یعنی نقطه تقاطع آنها) همین را نشان می دهد. ساختار به عنوان گزاره ها هندسه فرافکنی را میتوان بهعنوان هندسه سازههایی با لبه مستقیم نیز دید . از آنجایی که هندسه تصویری ساختارهای قطب نما را مستثنی می کند ، هیچ دایره، هیچ زاویه، هیچ اندازه گیری، هیچ موازی، و هیچ مفهومی از واسطه وجود ندارد . مشخص شد که قضایایی که در هندسه تصویری کاربرد دارند، گزارههای سادهتری هستند. به عنوان مثال، بخش های مخروطی مختلفهمگی در هندسه تصویری (مختلط) معادل هستند و برخی از قضایای دایره ها را می توان به عنوان موارد خاص این قضایای عمومی در نظر گرفت.
در اوایل قرن نوزدهم، کار ژان ویکتور پونسله ، لازار کارنو و دیگران هندسه تصویری را به عنوان یک رشته مستقل از ریاضیات تثبیت کردند . پایه های دقیق آن توسط کارل فون استادت مورد توجه قرار گرفت و توسط ایتالیایی ها جوزپه پیانو ، ماریو پیری ، الساندرو پادوآ و جینو فانو در اواخر قرن نوزدهم تکمیل شد. هندسه تصویری، مانند هندسه افین و اقلیدسی ، همچنین می تواند از برنامه ارلانگن فلیکس کلاین توسعه یابد. هندسه تصویری با مشخصهمتغیرهای تحت تبدیل گروه تصویری .
بنابراین، پس از کار زیاد روی تعداد بسیار زیاد قضایای موضوع، مبانی هندسه تصویری درک شد. ساختار بروز و نسبت متقاطع متغیرهای اساسی تحت تحولات تصویری هستند. هندسه فرافکنی را می توان با صفحه افین (یا فضای نزدیک) به اضافه یک خط (ابر صفحه) "در بی نهایت" مدل کرد و سپس آن خط (یا ابر صفحه) را "معمولی" در نظر گرفت. یک مدل جبری برای انجام هندسه تصویری به سبک هندسه تحلیلی با مختصات همگن ارائه شده است. از سوی دیگر، مطالعات بدیهی وجود هواپیماهای غیر دسارگوزی را نشان داد.مثالهایی برای نشان دادن اینکه بدیهیات وقوع را میتوان (فقط در دو بعد) توسط ساختارهایی که برای استدلال از طریق سیستمهای مختصات همگن قابل دسترسی نیستند، مدلسازی کرد.
در مفهوم بنیادی، هندسه تصویری و هندسه مرتب ابتدایی هستند زیرا حداقل بدیهیات را در بر می گیرند و می توانند به عنوان پایه ای برای هندسه همبستگی و اقلیدسی استفاده شوند. هندسه فرافکنی مرتب نیست و بنابراین پایه و اساس مشخصی برای هندسه است.
تاریخ
[ویرایش]اولین خصوصیات هندسی ماهیت تصویری در قرن سوم توسط پاپوس اسکندریه کشف شد. فیلیپو برونلسکی (1404-1472) بررسی هندسه پرسپکتیو را در طول سال 1425 آغاز کرد ( به تاریخچه پرسپکتیو مراجعه کنید تا یک بحث کاملتر در مورد کار در هنرهای زیبا که انگیزه بسیاری از توسعه هندسه تصویری بود). یوهانس کپلر (1571-1630) و جرارد دزارگ (1591-1661) به طور مستقل مفهوم "نقطه در بی نهایت" را توسعه دادند. Desargues با تعمیم استفاده از نقاط ناپدید برای شامل مواردی که این نقاط بسیار دور هستند، روشی جایگزین برای ساختن نقشه های پرسپکتیو ایجاد کرد. او هندسه اقلیدسی را ، که در آن خطوط موازی واقعاً موازی هستند، به یک مورد خاص از یک سیستم هندسی فراگیر تبدیل کرد. مطالعه Desargues در مورد مقاطع مخروطی توجه بلز پاسکال 16 ساله را به خود جلب کرد و به او کمک کرد تا قضیه پاسکال را فرموله کند . کارهای گاسپارد مونگ در پایان قرن 18 و آغاز قرن 19 برای توسعه بعدی هندسه تصویری مهم بود. کار دزارگ نادیده گرفته شد تا اینکه میشل شزلز در طول سال 1845 به یک نسخه دست نویس دست یافت.ژان ویکتور پونسله در سال 1822 رساله اساسی در مورد هندسه تصویری منتشر کرد. رابطه بین خواص متریک و تصویری هندسههای غیر اقلیدسی که به زودی پس از آن کشف شدند، در نهایت نشان دادند که دارای مدلهایی مانند مدل کلاین فضای هذلولی هستند که به هندسه تصویری مربوط میشود.
در سال 1855 AF Möbius مقاله ای در مورد جایگشت، که اکنون تبدیلات موبیوس نامیده می شود ، از دایره های تعمیم یافته در هواپیمای پیچیده نوشت . این دگرگونی ها نمایانگر فرافکنی های خط تصویری پیچیده هستند . در مطالعه خطوط در فضا، جولیوس پلوکر از مختصات همگن در توصیف خود استفاده کرد، و مجموعه خطوط بر روی ربع کلاین ، یکی از مشارکت های اولیه هندسه تصویری در زمینه جدیدی به نام هندسه جبری ، که شاخه ای از هندسه تحلیلی است، مشاهده شد. با ایده های فرافکنی
هندسه فرافکنی در اعتبار سنجی گمانه زنی های لوباچفسکی و بولیایی در مورد هندسه هذلولی با ارائه مدل هایی برای صفحه هذلولی بسیار مهم بود : برای مثال، مدل دیسک پوانکاره که در آن دایره های تعمیم یافته عمود بر دایره واحد با "خطوط هایپربولیک" مطابقت دارند ( ژئودزیک ). ) و «ترجمههای» این مدل با تبدیلهای موبیوس توصیف میشوند که دیسک واحد را به خودش ترسیم میکند. فاصله بین نقاط توسط یک متریک Cayley-Klein داده می شود که در ترجمه ها ثابت است زیرا به نسبت متقاطع بستگی دارد.، یک تغییر ناپذیر تصویری کلیدی. ترجمه ها به صورت ایزومتریک در نظریه فضای متریک ، به طور رسمی به عنوان تبدیل های کسری خطی ، و به عنوان تبدیل های خطی تصویری گروه خطی تصویری ، در این مورد SU(1,1) توصیف می شوند.
کار Poncelet ، یاکوب اشتاینر و دیگران در نظر گرفته نشده بود برای گسترش هندسه تحلیلی. قرار بود تکنیکها ترکیبی باشند : در واقع فضای تصویری همانطور که اکنون فهمیده میشود باید به صورت بدیهی معرفی شود. در نتیجه، فرمول بندی مجدد کار اولیه در هندسه تصویری به طوری که استانداردهای فعلی دقت را برآورده کند، می تواند تا حدودی دشوار باشد. حتی در مورد صفحه نمایشی به تنهایی، رویکرد بدیهی می تواند به مدل هایی منجر شود که از طریق جبر خطی قابل توصیف نیستند .
این دوره در هندسه با تحقیق بر روی منحنی جبری عمومی توسط کلبش ، ریمان ، ماکس نوتر و دیگران پیشی گرفت، که تکنیک های موجود را گسترش داد، و سپس توسط نظریه ثابت . در اواخر قرن، مکتب هندسه جبری ایتالیا ( Enriques ، Segre ، Severi ) از موضوع سنتی به منطقه ای تبدیل شد که نیاز به تکنیک های عمیق تر داشت.
در اواخر قرن نوزدهم، مطالعه دقیق هندسه تصویری کمتر مد شد، اگرچه ادبیات حجیم است. برخی از کار مهم در هندسه شمارشی به ویژه انجام شد، توسط شوبرت، که در حال حاضر به عنوان پیش بینی نظریه کلاس های Chern در نظر گرفته شده، به عنوان نمایندگی توپولوژی جبری Grassmannians .
هندسه فرافکنی بعدها کلید اختراع مکانیک کوانتومی پل دیراک شد . در سطح بنیادی، کشف این که اقدامات کوانتومی ممکن است در رفت و آمد با شکست مواجه شوند ، هایزنبرگ را آشفته و منصرف کرده بود ، اما مطالعه قبلی هواپیماهای پرتابی بر روی حلقههای غیرقابل جابهجایی احتمالاً دیراک را حساستر کرده بود. دیراک در کارهای پیشرفتهتر، از نقاشیهای گستردهای در هندسه تصویری برای درک معنای شهودی معادلات خود استفاده کرد، قبل از اینکه کار خود را با فرمالیسم منحصراً جبری بنویسد.
شرح
[ویرایش]وابسته کمتر محدود کننده است . این یک هندسه ذاتا غیر متریک است، به این معنی که حقایق مستقل از هر ساختار متریک هستند. تحت تبدیل های تصویری، ساختار بروز و رابطه مزدوج های هارمونیک تصویری حفظ می شود. محدوده تصویری پایه یک بعدی است. هندسه فرافکنی یکی از اصول اصلی هنر پرسپکتیو را رسمیت می بخشد: این که خطوط موازی در بی نهایت به هم می رسند.، و بنابراین به این صورت ترسیم می شوند. در اصل، هندسه تصویری را میتوان بهعنوان امتداد هندسه اقلیدسی در نظر گرفت که در آن «جهت» هر خط در درون خط بهعنوان یک «نقطه» اضافه میشود، و در آن «افق» جهتهای متناظر با خطوط همسطح است. به عنوان یک "خط" در نظر گرفته می شود. بنابراین، دو خط موازی در یک خط افق به دلیل ترکیب جهت یکسانی به هم می رسند.
جهت های ایده آل به عنوان نقاط در بی نهایت نامیده می شوند، در حالی که افق های ایده آل به عنوان خطوط در بی نهایت نامیده می شوند. به نوبه خود، تمام این خطوط در هواپیما در بی نهایت قرار دارند. با این حال، بینهایت یک مفهوم متریک است، بنابراین یک هندسه صرفاً تصویری هیچ نقطه، خط یا صفحهای را در این زمینه مشخص نمیکند – آنهایی که در بینهایت هستند، درست مانند سایرین رفتار میشوند.
از آنجا که یک هندسه اقلیدسی در یک هندسه تصویری قرار می گیرد - با هندسه تصویری که پایه ساده تری دارد - نتایج کلی در هندسه اقلیدسی ممکن است به شیوه ای شفاف تر به دست آید، جایی که قضایای جداگانه اما مشابه هندسه اقلیدسی ممکن است به طور جمعی در چارچوب پروژه مورد بررسی قرار گیرند. هندسه. برای مثال، خطوط موازی و غیر موازی نباید به عنوان موارد جداگانه در نظر گرفته شوند. بلکه یک صفحه نمایشی دلخواه به عنوان صفحه ایده آل مشخص می شود و با استفاده از مختصات همگن "در بی نهایت" قرار می گیرد.
منابع
[ویرایش]https://en.m.wikipedia.org/wiki/Projective_geometry
https://fa.m.wikipedia.org/wiki/هندسه_تصویری#/languages
هندسه تحلیلی
در ریاضیات،هندسه تحلیلی ، که به هندسه مختصات یا هندسه دکارتی نیز معروف است، مطالعه هندسه با استفاده از سیستم مختصات است . این در تضاد با هندسه مصنوعی است .
هندسه تحلیلی در فیزیک و مهندسی و همچنین در هوانوردی , موشک , علوم فضایی و پروازهای فضایی استفاده می شود . این پایه و اساس بیشتر زمینه های مدرن هندسه، از جمله هندسه جبری ، دیفرانسیل ، گسسته و محاسباتی است .
معمولاً سیستم مختصات دکارتی برای دستکاری معادلات برای صفحات، خطوط مستقیم و دایره ها، اغلب در دو و گاهی اوقات سه بعدی استفاده می شود. از نظر هندسی، صفحه اقلیدسی (دو بعدی) و فضای اقلیدسی را مطالعه می کند. همانطور که در کتاب های مدرسه آموزش داده شده است، هندسه تحلیلی را می توان ساده تر توضیح داد: این هندسه به تعریف و نمایش اشکال هندسی به روش عددی و استخراج اطلاعات عددی از تعاریف و نمایش های عددی اشکال مربوط می شود. اینکه جبر اعداد حقیقی را می توان برای به دست آوردن نتایجی در مورد پیوستار خطی هندسه به کار برد، به اصل اصل کانتور-ددکیند متکی است.
تاریخ(به ترتیب)
[ویرایش]یونان باستان
[ویرایش]ریاضیدان یونانی منائخموس با استفاده از روشی که شباهت زیادی به استفاده از مختصات داشت و گاهی اوقات گفته می شود که او هندسه تحلیلی را معرفی کرده است، مسائل را حل کرده و قضایا را اثبات می کند .
آپولونیوس از پرگا ، در بخش معین ، با مسائل به شیوه ای برخورد کرد که می توان آن را هندسه تحلیلی یک بعدی نامید. با سؤال یافتن نقاطی در یک خط که نسبت به سایرین باشد. آپولونیوس در سونیس روشی را توسعه داد که بسیار شبیه به هندسه تحلیلی است که گاهی اوقات تصور می شود کار او کار دکارت را پیش بینی کرده است.تا حدود 1800 سال استفاده او از خطوط مرجع، قطر و مماس اساساً هیچ تفاوتی با استفاده مدرن ما از یک قاب مختصات ندارد، جایی که فواصل اندازهگیری شده در امتداد قطر از نقطه مماس عبارتند از ابسیساها، و قطعات موازی با مماس و قطع شده بین محور و منحنی مختصات هستند. او بیشتر روابط بین ابسیساها و دستورات مربوطه را توسعه داد که معادل معادلات بلاغی (بیان شده در کلمات) منحنی ها هستند. با این حال، اگرچه آپولونیوس به توسعه هندسه تحلیلی نزدیک شده بود، اما موفق به انجام این کار نشد زیرا قدرهای منفی را در نظر نمی گرفت و در هر مورد سیستم مختصات به جای پیشینی بر یک منحنی معین به صورت پسینی قرار می گرفت.. یعنی معادلات با منحنی تعیین می شدند، اما منحنی ها با معادلات تعیین نمی شدند. مختصات، متغیرها و معادلات مفاهیم فرعی بودند که برای یک موقعیت هندسی خاص اعمال می شدند.
ایران
[ویرایش]عمر خیام ، ریاضیدان ایرانی قرن یازدهم، زمانی که با حل هندسی معادلات مکعب عمومی کمک کرد شکاف بین جبر عددی و هندسی کند، رابطه قوی بین هندسه و جبر مشاهده کرد و در مسیر درست حرکت کرد. اما گام تعیین کننده بعداً با دکارت رسید. عمر خیام را به شناسایی مبانی هندسه جبری نسبت می دهند و کتاب رساله او در برهان المسائل جبر (1070) که اصول هندسه تحلیلی را بیان می کند، بخشی از پیکره ریاضیات فارسی است که در نهایت منتقل شد. به اروپا. خیام به دلیل رویکرد دقیق هندسی او به معادلات جبری، را می توان پیشروی دکارت در ابداع هندسه تحلیلی دانست.
اروپا
[ویرایش]هندسه تحلیلی به طور مستقل توسط رنه دکارت و پیر دو فرما ابداع شد ، اگرچه گاهی اوقات به دکارت اعتبار میدهند. هندسه دکارتی ، اصطلاح جایگزینی که برای هندسه تحلیلی استفاده می شود، از نام دکارت نامگذاری شده است.
دکارت با روشهای مقالهای با عنوان [۸]La Géométrie (هندسه) ، یکی از سه مقاله همراه (ضمائم) منتشر شده در سال 1637 همراه با گفتار او در مورد روش هدایت صحیح عقل و جستجوی حقیقت در علوم ، پیشرفت چشمگیری داشت. از آن به عنوان گفتمان در مورد روش یاد می شود. La Geometrie ، که به زبان مادری فرانسوی خود نوشته شده است ، و اصول فلسفی آن، پایه ای برای حساب دیفرانسیل و انتگرال در اروپا فراهم کرد. در ابتدا این کار به خوبی مورد استقبال قرار نگرفت، تا حدی به دلیل شکاف های فراوان در استدلال ها و معادلات پیچیده. تنها پس از ترجمه به لاتین و اضافه شدن تفسیر توسطون شوتن در سال 1649 (و کارهای بعدی پس از آن) شاهکار دکارت مورد توجه قرار گرفت.
پیر دو فرما نیز پیشگام توسعه هندسه تحلیلی بود. اگرچه در زمان حیات او منتشر نشده بود، یک فرم خطی از Ad locos planos et solidos isagoge (مقدمه ای بر مکان و مکان جامد) در پاریس در سال 1637، درست قبل از انتشار گفتار دکارت، در گردش بود . به وضوح نوشته شده و به خوبی پذیرفته شده است، مقدمههمچنین زمینه را برای هندسه تحلیلی فراهم کرد. تفاوت اصلی بین رفتارهای فرما و دکارت یک موضوع دیدگاه است: فرما همیشه با یک معادله جبری شروع میکرد و سپس منحنی هندسی را توصیف میکرد که آن را برآورده میکرد، در حالی که دکارت با منحنیهای هندسی شروع کرد و معادلات آنها را به عنوان یکی از چندین ویژگی منحنیها تولید کرد. . در نتیجه این رویکرد، دکارت مجبور شد با معادلات پیچیدهتری سر و کار داشته باشد و او مجبور شد روشهایی را برای کار با معادلات چند جملهای درجه بالاتر توسعه دهد. این لئونارد اویلر بود که برای اولین بار روش مختصات را در مطالعه سیستماتیک منحنی ها و سطوح فضا به کار برد.
تعریف سیستم مختصات ها
[ویرایش]تعریف مختصات
[ویرایش]در هندسه تحلیلی، به صفحه یک سیستم مختصات داده می شود که به وسیله آن هر نقطه دارای یک جفت مختصات اعداد حقیقی است. به طور مشابه، به فضای اقلیدسی مختصاتی داده می شود که در آن هر نقطه دارای سه مختصات است. مقدار مختصات به انتخاب نقطه مبدا اولیه بستگی دارد. انواع مختلفی از سیستم های مختصات استفاده می شود، اما رایج ترین آنها موارد زیر است:
مختصات دکارتی
[ویرایش]سیستم مختصات دکارتی در یک صفحه یک سیستم مختصاتی است که هر نقطه را منحصراً با یک جفت مختصات عددی مشخص می کند . که فواصل علامت گذاری شده تا نقطه از دو خط ثابت عمود بر هم هستند که در یک واحد طول اندازه گیری می شوند.. هر خط مختصات مرجع یک محور مختصات یا محور ( محورهای جمع ) سیستم نامیده می شود و نقطه ای که آنها به هم می رسند مبدا آن است ، در جفت مرتب شده (0، 0) . مختصات همچنین می تواند به عنوان موقعیت های برجستگی عمود نقطه بر روی دو محور تعریف شود که به صورت فاصله علامت دار از مبدا بیان می شود.
میتوان از همین اصل برای تعیین موقعیت هر نقطه در فضای سهبعدی با سه مختصات دکارتی، فواصل علامتدار آن تا سه صفحه متقابل عمود بر هم (یا بهطور معادل، با طرحریزی عمود بر سه خط متقابل متقابل) استفاده کرد. به طور کلی، n مختصات دکارتی (عنصری از فضای n واقعی ) نقطه را در فضای اقلیدسی n بعدی برای هر بعد n مشخص می کند. این مختصات، تا علامت ، با فواصل از نقطه تا n ابرصفحه متقابل عمود بر هم برابر هستند .
اختراع مختصات دکارتی در قرن هفدهم توسط رنه دکارت ( نام لاتین شده : Cartesius ) با ایجاد اولین پیوند سیستماتیک بین هندسه اقلیدسی و جبر ، انقلابی در ریاضیات ایجاد کرد . با استفاده از سیستم مختصات دکارتی، اشکال هندسی (مانند منحنی ها) را می توان با معادلات دکارتی توصیف کرد: معادلات جبری شامل مختصات نقاطی که روی شکل قرار دارند. به عنوان مثال، دایره ای با شعاع 2 که در مرکز مبدأ صفحه قرار دارد، ممکن است به عنوان مجموعه ای از تمام نقاطی که مختصات آنها x و y است توصیف شود.معادله x 2 + y 2 = 4 را برآورده کنید .
مختصات دکارتی شالوده هندسه تحلیلی هستند و برای بسیاری از شاخه های دیگر ریاضیات مانند جبر خطی ، آنالیز مختلط ، هندسه دیفرانسیل، حساب چند متغیره ، نظریه گروه و غیره، تفاسیر هندسی روشنگر ارائه می دهند. یک مثال آشنا مفهوم نمودار یک تابع است. مختصات دکارتی نیز ابزارهای ضروری برای اکثر رشته های کاربردی هستند که با هندسه سروکار دارند، از جمله نجوم ، فیزیک ، مهندسی و بسیاری دیگر. آنها رایج ترین سیستم مختصات مورد استفاده در گرافیک کامپیوتری هستند ،طراحی هندسی به کمک کامپیوتر و سایر پردازش داده های مرتبط با هندسه .
مختصات قطبی
[ویرایش]در ریاضیات ، سیستم مختصات قطبی یک سیستم مختصات دو بعدی است که در آن هر نقطه از یک صفحه با فاصله از یک نقطه مرجع و یک زاویه از یک جهت مرجع تعیین می شود. نقطه مرجع (مشابه منشا یک سیستم مختصات دکارتی ) قطب نامیده می شود و پرتوی از قطب در جهت مرجع، محور قطبی است . فاصله از قطب را مختصات شعاعی ، فاصله شعاعی یا به سادگی شعاع می نامندو زاویه را مختصات زاویه ای ، زاویه قطبی یا آزیموت می نامند . زوایای نماد قطبی معمولاً در درجه یا رادیان بیان میشوند (rad)2π)برابر با 360 درجه است).
مختصات کروی
[ویرایش]در ریاضیات مختصات کروی،برای فضای سه بعدی است که در آن موقعیت یک نقطه با سه عدد مشخص می شود: فاصله شعاعی آن نقطه از یک مبدأ ثابت، زاویه قطبی آن اندازه گیری شده از یک جهت اوج ثابت ، و زاویه متعامد برآمدگی متعامد آن بر روی صفحه مرجعی که از مبدا می گذرد و متعامد به نقطه اوج است، از یک جهت مرجع ثابت در آن صفحه اندازه گیری می شود. می توان آن را نسخه سه بعدی سیستم مختصات قطبی دید .
مختصات استوانه ای
[ویرایش]یک سیستم مختصات استوانه ای یک سیستم مختصات سه بعدی است که موقعیت نقطه را با فاصله از یک محور مرجع انتخابی (محور L در تصویر مقابل)، جهت از محور نسبت به یک جهت مرجع انتخابی (محور A) مشخص می کند. فاصله از صفحه مرجع انتخاب شده عمود بر محور (صفحه حاوی بخش بنفش). بسته به اینکه کدام طرف صفحه مرجع رو به نقطه است، فاصله اخیر به عنوان یک عدد مثبت یا منفی داده می شود. یک سیستم مختصات استوانهای با مبدا O، محور قطبی A و محور طولی L. نقطه نقطه با فاصله شعاعی ρ = 4، مختصات زاویهای φ = 130 درجه و ارتفاع z = 4 است.
منابع
[ویرایش]https://en.m.wikipedia.org/wiki/Analytic_geometry
هندسه جبری
هندسهٔ جبری شاخهای از ریاضیات است که بهطور سنتی به مطالعهٔ صفرهای چندجملهای های چند متغیره میپردازد. هندسهٔ جبری مدرن بر اساس استفاده از تکنیکهای جبر مجرد بنا شده که اساساً از جبر جابجایی استفاده میکند تا مسائل هندسی مربوط به این مجموعه صفرها (ریشه این چند جملهایها) را مطالعه کند.
اشیای بنیادی که در مطالعه هندسه جبری استفاده میشوند واریتههای جبریاند که بیان هندسی حل دستگاهی از معادلات چند جملهایاند. بیشترین واریتههای جبری مطالعه شده خمهای جبری صفحهاند که شامل خطوط، دایرهها، سهمیها، بیضیها، هذلولیها، خمهای مکعبی مثل خمهای بیضوی و خمهای درجه چهار مثل lemniscateها و Cassini ovalها میباشند. یک نقطه از صفحه به خم بیضوی متعلق است اگر مختصات آن در یک معادلهٔ چند جملهای دادهشده صدق کند. سوالات بنیادی مربوط به مطالعهٔ نقاط خاصی مثل نقاط تکین، نقاط عطف و نقاط در بینهایت میباشد. سوالات پیشرفتهتر مرتبط میشوند به توپولوژی خم و معادلات بین خمهای داده شده بهوسیله معادلات مختلف.
نقش و کاربرد
[ویرایش]هندسه جبری نقش محوری در ریاضیات مدرن ایفا کرده و پیوندهای مفهومی چندگانهای با شاخههای گستردهای از ریاضیات چون آنالیز مختلط، توپولوژی و نظریه اعداد دارد. در ابتدا مطالعهٔ دستگاه معادلات چند جملهایهای چند متغیره موضوع هندسه جبری بود، آنجا که حل معادله از نظر خارج شده و فهمیدن خواص ذاتی جواب دستگاه معادلات اهمیت بیشتری پیدا میکند، آنجاست که هندسه جبری ظاهر میشود؛ چرا که در این مرحله دیگر یک جواب خاص اهمیت چندانی در مقابل آن خواص ندارد، این ما را به برخی قلمروها میکشاند که برخی از آنها جزو عمیقترین قلمروهای ریاضی هستند، چه از نظر مفهومی یا تکنیکی.
در قرن بیستم
[ویرایش]در قرن بیستم، هندسه جبری به چندین زیرمجموعه تقسیمبندی شدند:
- جریان اصلی هندسه جبری به مطالعه نقاط مختلط واریتههای جبری و بهطور عمومیتر نقاطی که مختصات آنها در میدان بسته جبری قرار دارند میپردازد.
- هندسه جبری حقیقی به مطالعه نقاط حقیقی یک واریته جبری میپردازد.
- هندسه سیالهای و بهطور عمومیتر هندسهٔ حساب به مطالعهٔ نقاط یک واریته جبری که مختصاتشان در میدانهای غیر بسته قرار دارند میپردازد، مثل میدانهایی که در نظریه جبری اعداد بحث میشوند چون اعداد گویا، میدانهای عددی، میدانهای متناهی، میدان توابع و میدان p-adicها.
- بخش عمده نظریه تکینگی به تکینگیهای واریتههای جبری میپردازد.
- هندسه جبری محاسباتی قلمرویی است که با ظهور رایانهها از برخورد هندسه جبری و جبر رایانهای بهوجود آمدهاست. این قلمرو عمدتاً شامل طراحی الگوریتم و توسعه نرمافزار برای مطالعه خواص بارز یک واریته داده شده میباشد.
بسیاری از پیشرفتهای جریان اصلی هندسه جبری در قرن بیستم در چارچوب جبر مجرد، صورت گرفت، با افزایش تأکید بر روی خواص «ذاتی» واریتههای جبری که وابسته به هیچکدام از روشهای متفاوت جاسازی آن واریته در فضای مختصاتی اطرافیش (ambient) وابسته نباشد؛ این هدف موازی با پیشرفت در شاخههایی چون توپولوژی، هندسه دیفرانسیل و هندسه مختلط میباشد. یکی از دستاوردهای کلیدی این هندسه جبری مجرد، نظریه اسکیم گروتندیک است که اجازه استفاده از نظریه شیفها برای مطالعهٔ واریتههای جبری را داده به طوری که این نحوه استفاده، شباهت بسیاری به استفاده از آن در مطالعه منیفلدهای دیفرانسیل و تحلیلی دارد. این دستاورد با توسعهٔ مفهوم نقطه بهوجود آمد؛ در هندسه جبری کلاسیک، یک نقطه از واریته آفین را از طریق قضیه صفرهای هیلبرت میتوان شناسایی کرد، بهوسیله یک ایدهآل ماکسیمال حلقه مختصاتی، در حالی که نقطه متناظر با آن در اسکیم آفین، همگی ایدهآلهای اولی از این حلقه میباشند. این بدین معناست که یک نقطه از چنین اسکیمی میتواند یا یک نقطه عادی، یا یک زیرواریته باشد. همچنین این رویکرد موجب اتحاد زبان و ابزارهای هندسه جبری کلاسیک گشته که بهطور عمده با نقاط مختلط، و نظریه جبری اعداد مرتبط میگردد. اثبات وایلز بر حدس فرما به نام قضیه آخر فرما که به مدت طولانی، حلناشدنی باقی مانده بود، اثباتی بر قدرت این رویکرد میباشد.
مفاهیم پایه ای
[ویرایش]صفرهای همزمان چند جمله ایها
[ویرایش]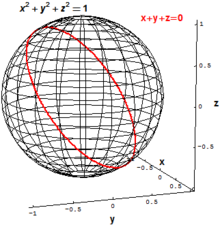
در هندسه جبری کلاسیک، علاقه اصلی بر روی اشیایی بود که بهطور همزمان مجموعهای از چند جملهایها را ناپدید میکنند (صفر میکنند)، یعنی مجموعه نقاطی که همزمان در یک یا تعداد بیشتری از معادلات چندجملهای صدق میکنند. به عنوان مثال، کره دوبُعدی با شعاع ۱ در فضای اقلیدسی را میتوان به صورت مجموعه تمام نقاط (x,y,z)ی تعریف کرد که در این معادله، صدق میکنند:
یک دایرهٔ «اریب» در را میتوان به صورت مجموعه نقاط (x,y,z) تعریف کرد که در دو معادلهٔ چندجملهای زیر، همزمان، صدق میکنند:
واریتههای آفین
[ویرایش]مقاله اصلی: واریتههای آفین
ابتدا با یک میدان شروع میکنیم. در هندسه جبری کلاسیک، این میدان، همیشه میدان اعداد مختلط بود؛ اما بسیاری از نتایج با فرض یک میدان جبره بستی چون هم، معتبر باقی خواهند ماند. ما فضای آفین بعدی روی را در نظر گرفته و آن را با نمایش میدهیم (یا صرفاً با ، هنگامی که در متن واضح باشد). هنگامی که دستگاه مختصات ثابت و مشخص باشد، میتوان را با یکی گرفت. هدف کار نکردن با این است که ساختار فضای برداری که با خود حمل میکند «فراموش» شود.
یک تابع را چندجملهای (یا منظم) گویند اگر آن را بتوان به صورت چندجملهای نوشت، یعنی اگر وجود داشته باشد چندجملهای چون در به گونهای که برای هر نقطه با مختصات در داشته باشیم .
هنگامی که یک دستگاه مختصات، انتخاب شد، توابع منظمِ روی n-فضای آفین را میتوان با حلقه توابع چندجملهای n متغیره روی یکی گرفت؛ به همین دلیل، مجموعه توابع منظم روی حلقه است و آن را با نمایش میدهند.
یک چندجملهای، در نقطهای ناپدید میشود اگر که مقدارش در آن نقطه، صفر شود. فرض کنید مجموعه تمام چندجملهایهای درون باشد. مجموعه ناپدیدشونده (یا مکان هندسی ناپدیدشونده یا مجموعه صفر) مجموعه شامل تمام نقاط درون است که هر چندجملهای بر روی آن، ناپدید میشوند؛ بهطور نمادین:
برای مجموعهای چون ، زیرمجموعه از را مجموعه جبری میگویند. مخفف کلمه varietry است (یک نوع خاص از مجموعههای جبری که در ادامه، تعریف شدهاست).
فرض کنید که مجموعهای مثل از داده شده باشد، آیا میتوان مجموعه تمام چندجملهایهایی که آن را تولید کردهاند را یافت؟ اگر زیرمجموعه دلخواهی از باشد، را به این صورت تعریف کنید: مجموعه تمام چندجملهایهایی که مجموعه صفرشان شامل باشد. اول کلمه ایدئال است: اگر دو چندجملهای و هر دو روی ناپدید (صفر) شوند، آنگاه هم روی ناپدید میشود، و اگر یک چندجملهای دلخواه باشد، آنگاه هم روی ناپدید شده؛ به همین دلیل، همیشه یک ایدهآل از حلقه چندجملهایهای است.
دو پرسش طبیعی، پیش میآید:
- برای یک زیرمجموعه دلخواه از ، چه زمان ؟
- برای یک مجموعه دلخواه از چندجملهایها چون ، چه زمان ؟
جواب سؤال اول با معرفی توپولوژی زاریسکی داده شد، یک توپولوژی روی که مجموعههای بسته آن، همان مجموعههای جبری هستند که بهطور مستقیم ساختار جبری را انعکاس میدهند. آنگاه اگر و تنها اگر یک مجموعه جبری یا یک مجموعه بسته زاریسکی باشد. جواب سؤال دوم توسط قضیه صفرهای هیلبرت داده میشود. یکی از شکلهای این قضیه میگوید که رادیکال ایدهآلهای تولید شده توسط است. به بیان مجردتر، یک ارتباط گالوایی، وجود دارد که منجر به ظهور دو عملگر بستار میگردد؛ آنها را میتوان شناسایی کرده و بهطور طبیعی، نقش بنیادینی در این نظریه بازی میکنند؛ مثال مربوط در بحث مربوط به ارتباط گالوایی، تشریح شدهاست.
به دلایل مختلف، ممکن است همیشه نخواهیم با کل ایدهآل مربوط به یک مجموعه جبری چون کار کنیم. قضیه بنیادی هیلبرت میگوید که ایدهآلهای درون همیشه متناهی، تولید شدهاند.
یک مجموعه جبری را تحویلناپذیر گویند اگر نتوان آن را به صورت اجتماع دو مجموعه جبری کوچکتر نوشت. هر مجموعه جبری به صورت اجتماع متناهی مجموعههای جبری تحویلناپذیر بوده و این تجزیه یکتاست؛ لذا عناصر آن را مؤلفههای تحویلناپذیر آن مجموعه جبری گویند. به یک مجموعه جبری تحویلناپذیر واریته هم میگویند. مشخص میشود که یک مجموعه جبری واریته (مجموعه جبری تحویلناپذیر) است اگر و تنها اگر به صورت مجموعه ناپدیدکننده (صفر کننده) یک ایدهآل اول از حلقه چندجملهای باشد.
برخی از مؤلفان، تمایز مشخصی بین مجموعههای جبری و واریتهها برقرار نمیکنند و در صورت لزوم از اصطلاح واریته تحویلناپذیر برای ایجاد چنین تمایزی استفاده میکنند.
توابع منظم
[ویرایش]مقاله اصلی: تابع منظم
درست همانگونه که توابع پیوسته نگاشتهای طبیعی روی فضاهای توپولوژی و توابع هموار نگاشتهای طبیعی روی منیفلدهای دیفرانسیلپذیر اند، دسته ای طبیعی از توابع روی یک مجموعه جبری نیز وجود دارند که به آنها توابع منظم یا توابع چندجمله ای گویند. یک تابع منظم روی مجموعه ای جبری چون در ، تحدید توابع منظم روی به مجموعه جبری است. برای یک مجموعه جبری که روی میدان اعداد مختلط تعریف شده باشد، توابع منظم هموار و حتی تحلیلی اند.
ممکن است الزام توسعه پذیر بودن یک تابع منظم به کل فضای پیرامونی (ambient) بهطور غیرطبیعی محدود کننده به نظر آید، اما این کار شباهت بسیاری به شرایط فضای توپولوژیکی نرمال دارد که در آن قضیه توسعه تیتز تضمین میکند که یک تابع پیوسته روی یک مجموعه بسته همیشه به فضای توپولوژیکی پیرامونی توسعه یابد.
توابع منظم روی ، درست همانند توابع منظم روی فضای آفینی، تشکیل یک حلقه میدهند که با نمایش داده میشود. این حلقه را حلقه مختصاتی روی مینامند.
از آنجا که توابع منظم روی از توابع منظم روی نشأت میگیرند، رابطه ای بین حلقههای مختصاتیشان وجود دارد. بهخصوص، اگر یک تابع منظم روی V تحدید دو تابع و در باشد، آنگاه هم یک تابع چند جمله ای خواهد بود که روی ناپدید شده و لذا به تعلق خواهد داشت. ازینرو، را میتوان با یکی گرفت.
هندسه جبری محاسباتی
[ویرایش]می توان تاریخ پیدایش هندسه جبری محاسباتی را به نشست EUROSAM'79 (سمپوزیوم بین المللی در مورد دستکاری نمادین و جبری) که در مارسی، فرانسه در ژوئن 1979 برگزار شد، دانست. دنیس اس. آرنون نشان داد که تجزیه جبری استوانه ای جورج کالینز (CAD) امکان محاسبه توپولوژی مجموعه های نیمه جبری را فراهم می کند. برونو بوخبرگر پایه های گروبنر و الگوریتم خود را برای محاسبه آنها ارائه کرد. دانیل لازارد الگوریتم جدیدی را برای حل سیستمهای معادلات چند جملهای همگن با پیچیدگی محاسباتی ارائه کرد که اساساً در تعداد راهحلهای مورد انتظار چند جملهای است و بنابراین به سادگی در تعداد مجهولات نمایی است. این الگوریتم به شدت با برآیند چند متغیره مکالی مرتبط است. از آن زمان، اکثر نتایج در این زمینه به یک یا چند مورد از این موارد یا با استفاده یا بهبود یکی از این الگوریتمها و یا با یافتن الگوریتمهایی که پیچیدگی آنها صرفاً در تعداد متغیرها تصاعدی است، مربوط میشود. مجموعهای از نظریههای ریاضی مکمل روشهای نمادین به نام هندسه جبری عددی در چند دهه گذشته توسعه یافته است. روش محاسباتی اصلی، ادامه هموتوپی است. برای مثال، این مدل از محاسبات ممیز شناور برای حل مسائل هندسه جبری پشتیبانی می کند.
بر اساس گروبنر
[ویرایش]مبنای گروبنر سیستمی از مولدهای یک ایده آل چند جمله ای است که محاسبه آن امکان کسر بسیاری از ویژگی های تنوع جبری وابسته را که با ایده آل تعریف می شود را فراهم می کند. با توجه به یک ایده آل I که مجموعه جبری V را تعریف می کند: V خالی است (بیش از یک پسوند جبری بسته از فیلد پایه)، اگر و فقط در صورتی که مبنای گروبنر برای هر ترتیب تک جمله ای به {1} کاهش یابد. با استفاده از سری هیلبرت می توان بعد و درجه V را از هر مبنای گروبنر از I برای یک مرتبه یکپارچه محاسبه کرد که درجه کل را اصلاح می کند. اگر بعد V 0 باشد، می توان نقاط (تعداد محدود) V را از هر مبنای گروبنر I محاسبه کرد (به سیستم معادلات چند جمله ای مراجعه کنید). یک محاسبات مبتنی بر گروبنر به شخص اجازه می دهد تا تمام اجزای تقلیل ناپذیر موجود در یک ابرسطح معین را از V حذف کند. یک محاسبات مبتنی بر گروبنر به فرد اجازه می دهد تا بسته شدن Zariski تصویر V را با طرح ریزی روی مختصات اولیه k، و زیر مجموعه ای از تصویر که در آن طرح ریزی مناسب نیست، محاسبه کند. به طور کلی تر، محاسبات مبتنی بر گروبنر به فرد اجازه می دهد تا بسته شدن Zariski تصویر و نقاط بحرانی یک تابع منطقی V را در یک نوع وابسته دیگر محاسبه کند. محاسبات مبتنی بر گروبنر به شخص اجازه نمی دهد که تجزیه اولیه I یا ایده آل های اولیه را که مؤلفه های تقلیل ناپذیر V را تعریف می کنند، مستقیماً محاسبه کند، اما اکثر الگوریتم ها برای این کار شامل محاسبات پایه گروبنر هستند. الگوریتمهایی که مبتنی بر پایههای گروبنر نیستند از زنجیرههای منظم استفاده میکنند، اما ممکن است در برخی شرایط استثنایی به پایههای گروبنر نیاز داشته باشند. محاسبه پایه های گروبنر دشوار است. در واقع، ممکن است در بدترین حالت، چند جملهای داشته باشند که درجه آنها از نظر تعداد متغیرها دوبرابر نمایی است و تعدادی چندجملهای که نیز دو برابر نمایی است. با این حال، این تنها یک پیچیدگی در بدترین حالت است، و محدودیت پیچیدگی الگوریتم لازارد در سال 1979 ممکن است اغلب اعمال شود. الگوریتم Faugère F5 این پیچیدگی را درک می کند، زیرا ممکن است به عنوان بهبود الگوریتم لازارد در سال 1979 در نظر گرفته شود. نتیجه این است که بهترین پیادهسازیها به فرد امکان میدهد تقریباً بهطور معمول با مجموعههای جبری با درجه بیش از 100 محاسبه کند. این بدان معناست که در حال حاضر، دشواری محاسبه بر اساس گروبنر به شدت با دشواری ذاتی مسئله مرتبط است.
تجزیه جبری استوانه ای (CAD)
[ویرایش]CAD الگوریتمی است که در سال 1973 توسط G. Collins برای پیاده سازی قضیه Tarski-Seidenberg در مورد حذف کمیت بر روی اعداد واقعی با پیچیدگی قابل قبولی معرفی شد. این قضیه به فرمول های منطق مرتبه اول مربوط می شود که فرمول های اتمی آن برابری های چند جمله ای یا نامساوی بین چندجمله ای ها با ضرایب واقعی است. بنابراین، این فرمول ها فرمول هایی هستند که ممکن است از فرمول های اتمی توسط عملگرهای منطقی و (∧)، یا (∨)، نه (¬)، برای همه (∀) و (∃) ساخته شوند. قضیه تارسکی بیان می کند که از روی چنین فرمولی می توان فرمول معادل را بدون کمیت (∀, ∃) محاسبه کرد. پیچیدگی CAD در تعداد متغیرها دو برابر است. این بدان معنی است که CAD در تئوری اجازه می دهد تا هر مسئله هندسه جبری واقعی را که ممکن است با چنین فرمولی بیان شود، حل کند، که تقریباً هر مشکلی در مورد انواع و مجموعه های نیمه جبری صریح داده شده است. در حالی که محاسبات مبتنی بر گروبنر فقط در موارد نادر دارای پیچیدگی نمایی مضاعف است، CAD تقریباً همیشه این پیچیدگی بالا را دارد. این به این معنی است که، مگر اینکه اکثر چند جمله ای های ظاهر شده در ورودی خطی باشند، ممکن است مشکلات بیش از چهار متغیر را حل نکند. از سال 1973، بیشتر تحقیقات در مورد این موضوع یا به بهبود CAD یا یافتن الگوریتم های جایگزین در موارد خاص مورد علاقه عمومی اختصاص یافته است. به عنوان نمونه ای از وضعیت هنر، الگوریتم های کارآمدی برای یافتن حداقل یک نقطه در هر جزء متصل از یک مجموعه نیمه جبری وجود دارد، و بنابراین برای آزمایش خالی بودن یک مجموعه نیمه جبری. از سوی دیگر، CAD هنوز در عمل بهترین الگوریتم برای شمارش تعداد اجزای متصل است.
=== پیچیدگی مجانبی در مقابل کارایی عملی === الگوریتمهای عمومی اولیه هندسه محاسباتی دارای پیچیدگی دوگانه در بدترین حالت هستند. به طور دقیق تر، اگر d حداکثر درجه چند جمله ای های ورودی و n تعداد متغیرها باشد، پیچیدگی آنها حداکثر برای است. مقداری ثابت c، و برای برخی از ورودیها، پیچیدگی حداقل برای یک ثابت دیگر c است. در طول 20 سال آخر قرن بیستم، الگوریتم های مختلفی برای حل مسائل فرعی خاص با پیچیدگی بهتر معرفی شده اند. اکثر این الگوریتمها دارای پیچیدگی هستند. در میان این الگوریتمها که یک مشکل فرعی از مسائل حل شده توسط پایههای گروبنر را حل میکنند، میتوان به «آزمایش در صورتی که یک تنوع وابسته خالی است» و «حل سیستمهای چند جملهای ناهمگن که تعداد راهحلهای محدودی دارند» اشاره کرد. چنین الگوریتمهایی عبارتند از. به ندرت اجرا می شود، زیرا در بیشتر مدخل ها، الگوریتم های F4 و F5 Faugère کارایی عملی بهتری دارند و احتمالاً پیچیدگی مشابه یا بهتری دارند ("احتمالا" زیرا ارزیابی پیچیدگی الگوریتم های مبتنی بر گروبنر در یک کلاس خاص از ورودی ها کار دشواری است. که تنها در چند مورد خاص انجام شده است). الگوریتم های اصلی هندسه جبری واقعی که یک مسئله حل شده توسط CAD را حل می کند به توپولوژی مجموعه های نیمه جبری مربوط می شود. ممکن است «شمارش تعداد مؤلفههای متصل»، «آزمایش دو نقطه در یک مؤلفه» یا «محاسبه طبقهبندی ویتنی از یک مجموعه جبری واقعی» استناد شود. آنها دارای پیچیدگی هستند، اما ثابت درگیر نماد "O" به قدری زیاد است که استفاده از آنها برای حل هر مشکل غیر ضروری که به طور موثر توسط CAD حل می شود، غیر ممکن است حتی اگر بتوان از تمام توان محاسباتی موجود در جهان استفاده کرد. بنابراین، این الگوریتمها هرگز پیادهسازی نشدهاند و این یک حوزه تحقیقاتی فعال برای جستجوی الگوریتمهایی است که در کنار هم از پیچیدگی مجانبی خوب و کارایی عملی خوبی برخوردار هستند.
منابع
[ویرایش]https://en.m.wikipedia.org/wiki/Algebraic_geometry#/editor/9
https://fa.m.wikipedia.org/wiki/هندسه_جبری#/languages
https://de.m.wikipedia.org/wiki/Algebraische_Geometrie
هندسه اقلیدسی
هندسه اقلیدسی، دستگاهی ریاضیاتی است که آن را به اقلیدس، ریاضیدان یونانی اهل اسکندریه نسبت میدهند، چرا که او در کتاب هندسه خود به نام اصول اقلیدس این نوع هندسه را توصیف نمود. روش اقلیدس شامل فرض گرفتن دسته کوچکی از اصول موضوعههای شهودی، و استنتاج گزارههای زیادی از این اصول میباشد. گرچه که بسیاری از نتایج اقلیدس توسط ریاضیدانان قبل تر از او هم بیان شده بودند، اقلیدس اولین کسی بود که که نشان داد چگونه میتوان این گزارهها را در یک دستگاه استنتاجی و منطقی جامع گنجاند. کتاب اصول اقلیدس، ابتدا از هندسه مسطحه شروع میکند که هنوز هم در آموزش متوسطه به عنوان اولین دستگاه اصول موضوعهای و اولین مثالها از اثباتهای ریاضیاتی تدریس میگردند. سپس این کتاب به مباحث اجسام صلب از فضای سه بعدی میپردازد. بخش اعظم کتاب اصول اقلیدس به بیان نتایجی میپردازد که اکنون به آن جبر و نظریه اعداد گفته شده و در آنجا به زبان هندسی بیان شدهاند.

پیشینه
[ویرایش]در حدود ۳۰۱ سال قبل از میلاد دنیای هندسه در تب و تاب بود. نظرات مختلفی در زمینهٔ هندسه وجود داشت و سرانجام اقلیدس با انتشار کتاب اصول بنیادی را بنا نهاد که تا قرنها منسجمترین بنیادهای نظری بشر محسوب میشد. روش اقلیدس ساده بود او چند اصل موضوع و چند اصل متعارف را بدون اثبات به عنوان اصول بدیهی پذیرفت و سپس بر اساس آن صدها قضیه دیگر را اثبات کرد که بیشتر آنها بسیار دور از ذهن بودند.
اقلیدس شاگرد مکتب افلاطون بود. او در اصول سیزده جلدی خود تمام دانش بشری تا آن زمان را گرد آورد که به مدت دو هزار سال به صورت مرجعی بیبدیل باقی ماند. روش بنداشتی (اصل موضوع) اقلیدس منجر به کاربرد الگویی شد که امروزه به آن ریاضیات محض میگوییم. محض از این نظر که با اندیشهٔ محض سر و کار دارد و از راه آزمون و خطا و تجربه به دست نمیآید و درستی یا نادرستی احکام آن را نیز از راه تجربه نمیتوان اثبات یا نفی کرد.
برای استفاده از روش بنداشتی یا اصل موضوع دو شرط را باید پذیرفت:
- شرط اول: پذیرفتن احکامی به نام بنداشت یا اصل موضوع که به هیچ توجیه دیگری نیاز نداشته باشند.
- شرط دوم: توافق بر اینکه کی و چگونه حکمی «بهطور منطقی» از حکم دیگر نتیجه میشود، یعنی توافق در برخی قواعد استدلال.
کار عظیم اقلیدس این بود که چند اصل ساده، چند حکم که بینیاز به توجیهی پذیرفتنی بودند دستچین کرد، و از آنها ۴۶۵ گزاره نتیجه گرفت. زیبایی کار اقلیدس در این است که این همه را از آن اندک نتیجه گرفت.
عناصر
[ویرایش]عناصر عمدتاً نظامبندی دانش قبلی از هندسه است. بهبود آن نسبت به درمان های قبلی به سرعت شناخته شد و در نتیجه علاقه کمی به حفظ درمان های قبلی وجود داشت و اکنون تقریباً همه آنها از بین رفته اند.درباب این عناصر 13تا کتاب نوشته شده بود.
اصل موضوعه
[ویرایش]تمامِ هندسهٔ اقلیدسی، میتواند از پنج اصلِ موضوعهٔ زیر استخراج شود:
- از هر دو نقطه متمایز، یک و تنها یک خط راست میگذرد.
- هر پارهخط را میتوان تا بینهایت رویِ خطِ راست امتداد داد.
- با یک نقطه به عنوانِ مرکز و یک پارهخط به عنوانِ شعاع میتوان یک دایره رسم نمود.
- همهٔ زوایایِ قائمه با هم برابرند. (این اصل معیاری طبیعی برای اندازهگیری زاویهها در اختیار میگذارد)
- اگر یک خط، دو خطِ دیگر را قطع کند، آن دو خط در طرفی که جمعِ زوایایِ داخلیِ تولید شده توسطِ خطِ مورب کمتر از دوقائمه است به هم میرسند (خود یا امتدادشان).
برایِ بیانِ این اصولِ موضوعه به مفاهیمی مانندِ نقطه و خط نیاز داریم. همانطور که باید چند گزاره را بدونِ اثبات بپذیریم تا بقیهٔ گزارهها استخراج شوند لازم است چند مفهوم را نیز بدونِ تعریف بپذیریم. به این مفاهیم «تعریفنشدهها» میگویند. همانطور که دیده میشود اصولِ هندسهٔ اقلیدسی به جز اصلِ پنجم بسیار ساده و بدیهی به نظر میآیند. به همیندلیل از زمانِ اقلیدس ریاضیدانانِ بیشماری در شرق و غرب (منجمله خیام ریاضیدانِ ایرانی) تلاش کردهاند اصلِ آزاردهندهٔ پنجم را به اثبات برسانند.اما این کار همواره با شکست رو به رو شد. سپس برخی ریاضیدانان تلاش نمودند خلافِ اصلِ پنجم را فرض کنند تا ببینند آیا هندسهای متناقض پدید میآید یا نه. از آنجا که هیچ تناقضی در هندسههایِ دارایِ اصلِ پنجمِ متفاوت دیده نشد به آنها نامِ هندسه نااقلیدسی را دادند. در نتیجه این مسئله مطرح گردید که تجربه کدام هندسه را تأیید میکند. نظریهٔ نسبیت عام به این پرسش پاسخ میدهد.
پس از اقلیدس
[ویرایش]تا ۲۱۰۰ سال پس از اقلیدس هندسهٔ او یگانه هندسهٔ موجود بود.بعد از او هندسه ای مثل هندسه اقلیدسی ولی عمیق تر که اسم آن نااقلیدسی بود توسط گاوس پایه گذاری شد.
سیستم اندازه گیری
[ویرایش]هندسه اقلیدسی دارای دو نوع اندازه گیری اساسی است: زاویه و فاصله . مقیاس زاویه مطلق است و اقلیدس از زاویه راست به عنوان واحد اصلی خود استفاده می کند، به طوری که برای مثال، یک زاویه 45 درجه به عنوان نیمی از زاویه قائم نامیده می شود. مقیاس فاصله نسبی است. یکی به دلخواه یک پاره خط با طول غیر صفر معینی را به عنوان واحد انتخاب می کند و سایر فواصل در رابطه با آن بیان می شوند. جمع کردن فواصل با ساختاری نشان داده می شود که در آن یک پاره خط در انتهای یک پاره خط دیگر کپی می شود تا طول آن افزایش یابد، و به طور مشابه برای تفریق.
اندازه گیری مساحت و حجم از فواصل بدست می آید. به عنوان مثال، یک مستطیل با عرض 3 و طول 4 دارای مساحتی است که نشان دهنده حاصلضرب است، 12. از آنجا که این تفسیر هندسی ضرب به سه بعد محدود می شد، هیچ راه مستقیمی برای تفسیر حاصل ضرب چهار یا بیشتر وجود نداشت. اعداد، و اقلیدس از چنین محصولاتی اجتناب می کند، اگرچه به طور ضمنی، برای مثال در اثبات کتاب نهم، گزاره 20، اشاره شده است.
اقلیدس به یک جفت خط، یا یک جفت شکل مسطح یا جامد، در صورتی که طول، مساحت یا حجم آنها به ترتیب برابر باشد، و به طور مشابه برای زاویه ها، به عنوان «مساو» (ἴσος) اطلاق می شود. اصطلاح قوی تر " همخوان " به این ایده اشاره دارد که یک شکل کامل به اندازه و شکل شکل دیگری است. از طرف دیگر، اگر بتوان یکی را روی دیگری جابهجا کرد تا دقیقاً با آن مطابقت داشته باشد، دو شکل همخوان هستند. (برگرداندن آن بر روی آن مجاز است.) بنابراین، برای مثال، یک مستطیل 2x6 و یک مستطیل 3x4 مساوی هستند اما متجانس نیستند و حرف R با تصویر آینه ای آن همخوانی دارد. به ارقامی که به جز اندازههای متفاوت با هم همخوانی دارند، مشابه نامیده میشوند . زوایای متناظر در یک جفت شکل مشابه همخوان هستند واضلاع متناظر با یکدیگر متناسب هستند.
کاربرد
[ویرایش]به دلیل موقعیت بنیادی هندسه اقلیدسی در ریاضیات، ارائه بیش از یک نمونه نمونه از کاربردها در اینجا غیرعملی است.
منابع
[ویرایش]https://en.m.wikipedia.org/wiki/Euclidean_geometry
هندسه نااقلیدسی
هندسه غیراقلیدسی یا نااقلیدوسی شامل دو هندسه مبتنی بر بدیهیات است که نزدیک به آنهایی است که هندسه اقلیدسی را مشخص می کنند . از آنجایی که هندسه اقلیدسی در تقاطع هندسه متریک و هندسه وابسته قرار دارد ، هندسه غیراقلیدسی با جایگزین کردن اصل موازی با یک جایگزین یا کاهش نیاز متریک به وجود می آید. در مورد اول، هندسه هذلولی و هندسه بیضوی ، هندسههای سنتی غیر اقلیدسی به دست میآیند. هنگامی که نیاز متریک آرام شد، در آن صورت صفحات همبسته مرتبط با جبرهای مسطح وجود دارد، که هندسه های سینماتیکی را به وجود می آورند که هندسه نااقلیدسی نیز نامیده می شود.
نمونه استدلال
[ویرایش]توازی دو خط چگونه است؟
[ویرایش]
هندسه نااقلیدوسی:رفتار خطوط با عمود مشترک در هر یک از سه نوع توازی به صورت بیضوی،اقلیدوسی یا خط راست و هذلولی مانند۱
هندسه اقلیدوسی:فاصلهٔ (عمودی) بین دو نیمخط هنگامی که به سمت راست حرکت میکنیم فاصلهٔ P تا Q باقی میمانند.۲
- ۱=به نمودار شماره یک مراجعه کنید(تعریف از راست به چپ است)
- ۲=قسمت وسط نموادر شماره یک ببینید.
گسترش
[ویرایش]هندسهٔ نااقلیدسی بعدها توسط گاوس و ریمان در قالب هندسهٔ کلّیتری بسط داده شدند. همین هندسهٔ کلیتر است که در نگرهٔ نسبیت عام اینشتین استفاده شدهاست. در هندسه نااقلیدوسی مجموعه زوایای داخلی مثلت ۱۸۰درجه نمیباشد. برای مثال اگر ضلعهای مثلث هذلولوی باشد مجموعه زوایای داخلی هیچگاه به۱۸۰درجه نمیرسد و کمتر میباشد. همچنین اگر هندسه بیضوی باشد، هیچگاه ۱۸۰ درجه نمیشود؛ بلکه بیشتر میباشد.
بدیهیات
[ویرایش]هندسه اقلیدسی را می توان به روش های مختلفی به صورت اصولی توصیف کرد. متأسفانه، سیستم اصلی اقلیدس متشکل از پنج اصل (بدیهیات) یکی از اینها نیست، زیرا براهین او بر چندین فرض بیان نشده تکیه می کنند که باید به عنوان بدیهیات نیز در نظر گرفته می شدند. سیستم هیلبرت متشکل از 20 بدیهیات از نزدیکترین رویکرد اقلیدس را دنبال می کند و توجیه همه براهین اقلیدس را فراهم می کند. سیستمهای دیگر، با استفاده از مجموعههای مختلف اصطلاحات تعریفنشده ، هندسه یکسانی را با مسیرهای مختلف به دست میآورند. با این حال، همه رویکردها بدیهی دارند که از نظر منطقی با فرض پنجم اقلیدس، یعنی اصل موازی، معادل است. هیلبرت از فرم بدیهی Playfair استفاده می کند، در حالی که Birkhoffبرای مثال، از این اصل استفاده میکند که میگوید: "یک جفت مثلث مشابه اما متجانس وجود دارد." در هر یک از این سیستمها، حذف یک اصل اصلی معادل اصل موازی، به هر شکلی که باشد، و دست نخورده ماندن همه بدیهیات دیگر، هندسه مطلق را ایجاد میکند . از آنجایی که 28 گزاره اول اقلیدس (در عناصر ) نیازی به استفاده از فرض موازی یا چیزی معادل آن ندارند، همه آنها گزاره های واقعی در هندسه مطلق هستند.
برای به دست آوردن یک هندسه غیر اقلیدسی، فرض موازی (یا معادل آن) باید با نفی آن جایگزین شود . نفی شکل بدیهی Playfair ، از آنجایی که یک دستور مرکب است (... یک و تنها یک وجود دارد ...)، می تواند به دو روش انجام شود:
- یا بیش از یک خط از طریق نقطه موازی با خط داده شده وجود خواهد داشت یا هیچ خطی در نقطه موازی با خط داده شده وجود نخواهد داشت. در حالت اول، جایگزینی فرض موازی (یا معادل آن) با عبارت "در یک صفحه، با توجه به نقطه P و خط l که از P نمی گذرد، دو خط از P وجود دارد که l را برآورده نمی کنند " و حفظ همه بدیهیات دیگر، هندسه هذلولی را نشان می دهد.
- مورد دوم به این راحتی قابل رسیدگی نیست. صرفاً جایگزین کردن فرض موازی با این جمله، "در یک صفحه، با توجه به نقطه P و خط l که از P نمی گذرد، تمام خطوط از طریق P با l ملاقات می کنند "، مجموعه ای از بدیهیات را به دست نمی دهد. از آنجایی که خطوط موازی در هندسه مطلق وجود دارند، نتیجه میشود اما این عبارت می گوید که هیچ خط موازی وجود ندارد. این مشکل برای خیام، ساکری و لامبرت (در ظاهری دیگر) شناخته شده بود و مبنایی برای رد آنچه به عنوان «مورد زاویه مبهم» شناخته میشد، شد. برای به دست آوردن مجموعه ای ثابت از بدیهیات که شامل این اصل در مورد نداشتن خطوط موازی می شود، برخی بدیهیات دیگر باید بهینه سازی شوند. این تنظیمات به سیستم بدیهی مورد استفاده بستگی دارد. از جمله، این ترفندها تأثیری بر تغییر فرض دوم اقلیدس از این جمله دارند که پارههای خط را میتوان به طور نامحدود به این جمله که خطوط نامحدود هستند گسترش داد. هندسه بیضوی ریمان به عنوان طبیعی ترین هندسه ای که این اصل را برآورده می کند ظاهر می شود.
منابع
[ویرایش]منابع موجود در ویکی پدیای فارسی
منابع موجود در ویکی پدیای انگلیسی
زاویه داخلی و خارجی
زاویهداخلی یا زاویهداخلی چندضلعی نوعی دیگر از زاویه است که در مورد اندازهگیری زاویه درون چندضلعی منتظم بهکارگیری میرود.
زاویهخارجی نوعی دیگر از زاویه است که در مورد اندازهگیری زاویه بیرون چندضلعی منتظم به کار میرود.

ویژگیها
[ویرایش]- در زاویهداخلی هرچقدر تعداد ضلعها بیشتر شود،اندازه زاویهداخلی بیشتر میشود.
- در زاویهخارجی هرچقدر تعداد ضلعها بیشتر شود،اندازه زاویه خارجی کمتر میشود.
- اگر زاویهداخلی را با زاویهخارجی جمع کنیم،برابر با°۱۸۰درجه میشود.
- زاویهداخلی و زاویهخارجی باهم مکمل هستند.
- مجموع زاویههای داخلی بستگی به تعداد ضلع چندضلعی منتظم دارد
- مجموع زاویههایی خارجی چندضلعی منتظم٬همیشه برابر با°۳۶۰درجه است
- مثلث متساوی الاضلاع تنها چندضلعی منتظم است که زاویهخارجی او بیشتر زاویهداخلی اش میباشد
- مجموع زاویه داخلی یک مثلث برای با°۱۸۰درجه است.
- مربع تنها چندضلعیمنتظم است که زاویه داخلی او برابر با زاویهخارجی او است.
اندازهگیری زاویه داخلی
[ویرایش]یک nضلعی منتظم را درنظر بگیرید.
ابتدا تعداد مثلث هایش را طبق چندضلعی های معروف محاسبه میکنیم
- مربع:۲مثلث
- پنج ضلعی منتظم:۳مثلث
- شش ضلعی منتظم:۴مثلث
- هفت ضلعی منتظم:۵مثلث
- هشت ضلعی منتظم:۶مثلث
- نه ضلعی منتظم:۷مثلث
- ده ضلعی منتظم:۸مثلث
چون مجموعه زاویههایی داخلی یک مثلث°۱۸۰درجه است پس مجموعه زاویههایی داخلی بر اساس مجموع زاویه های تعداد مثلث های دورن او است.تعداد مثلث:
اندازه زاویهداخلی چندضلعی منتظم برابر با تقسیم تعداد ضلعها است.چون تعداد راس ها با تعداد ضلعها برابر است.مجموع زاویه داخلی:
اندازه زاویهداخلی:
اندازه زاویه خارجی
[ویرایش]مجموع زاویه خارجی:360درجه اندازه زاویه خارجی:
مجموع اندازه زاویه داخلی وجه های چندوجهی منتظم
[ویرایش]که در اینجاnبرابر با تعداد وجه ها است،و'nتعداد ضلع وجه های چندوجهی منتظم است.اندازه زاویه داخلی چندوجهی منتظم:
جدول زاویه های داخلی
[ویرایش]| نام چندضلعی | مجموع زاویه داخلی | اندازه زاویه داخلی | اندازه زاویه خارجی |
|---|---|---|---|
| مثلث متساوی الاضلاع | |||
| مربع | |||
| پنج ضلعی منتظم | |||
| شش ضلعی منتظم | |||
| هشت ضلعی
منتظم |
|||
| نه ضلعی منتظم | |||
| ده ضلعی منتظم | |||
| دوازده ضلعی منتظم | |||
| پانزده ضلعی منتظم | |||
| شانزده ضلعی منتظم | |||
| بیست ضلعی منتظم | |||
| بیست و چهار ضلعی منتظم | |||
| سی ضلعی منتظم | |||
| سی و دو ضلعی منتظم | |||
| سی و شش ضلعی منتظم | |||
| چهل ضلعی منتظم | |||
| شصت ضلعی منتظم | |||
| نود ضلعی منتظم | |||
| صد ضلعی منتظم | |||
| صد و بیست ضلعی منتظم |
منابع
[ویرایش]- ریاضیات پایههشتم/فصل سوم/درس چهارم/۱۴۰۱
- ریاضیات پایههشتم/فصل سوم/درس پنجم/۱۴۰۱
مختصات کروی
در ریاضیات مختصات کروی،برای فضای سه بعدی است که در آن موقعیت یک نقطه با سه عدد مشخص می شود: فاصله شعاعی آن نقطه از یک مبدأ ثابت، زاویه قطبی آن اندازه گیری شده از یک جهت اوج ثابت ، و زاویه متعامد برآمدگی متعامد آن بر روی صفحه مرجعی که از مبدا می گذرد و متعامد به نقطه اوج است، از یک جهت مرجع ثابت در آن صفحه اندازه گیری می شود. می توان آن را نسخه سه بعدی سیستم مختصات قطبی دید .
استفاده از نمادها و ترتیب مختصات در منابع و رشته ها متفاوت است. این مقاله از کنوانسیون ISO که اغلب در فیزیک با آن مواجه میشود، استفاده میکند :فاصله شعاعی، زاویه قطبی و زاویه ازیموت را نشان می دهد. در بسیاری از کتاب های ریاضی،یافاصله شعاعی، زاویه ازیموتال و زاویه قطبی را نشان میدهد و معانی θ و φ را تغییر میدهد . قراردادهای دیگری نیز استفاده می شود، مانند r برای شعاع از محور z ، بنابراین باید دقت زیادی برای بررسی معنای نمادها انجام شود.
طبق قراردادهای سیستم های مختصات جغرافیایی ، موقعیت ها با طول و عرض جغرافیایی و ارتفاع (ارتفاع) اندازه گیری می شوند. تعدادی سیستم مختصات آسمانی بر اساس صفحات بنیادی مختلف و با اصطلاحات مختلف برای مختصات مختلف وجود دارد. سیستم های مختصات کروی مورد استفاده در ریاضیات معمولاً به جای درجه از رادیان استفاده می کنند و زاویه آزیموتال را در خلاف جهت عقربه های ساعت از محور x به محور y اندازه می گیرند نه در جهت عقربه های ساعت از شمال (0 درجه) به شرق (90 درجه) مانند سیستم مختصات افقی . . زاویه قطبی اغلب با زاویه جایگزین می شودزاویه ارتفاع از صفحه مرجع اندازه گیری می شود، به طوری که زاویه ارتفاع صفر در افق باشد.
سیستم مختصات کروی سیستم مختصات قطبی دو بعدی را تعمیم می دهد. همچنین می توان آن را به فضاهای با ابعاد بالاتر گسترش داد و سپس به عنوان یک سیستم مختصات ابرکره ای نامیده می شود .

منابع
[ویرایش]https://en.m.wikipedia.org/wiki/Spherical_coordinate_system
درحال تحقیق
مختصات استوانه ای
یک سیستم مختصات استوانهای یک سیستم مختصات سه بعدی است که موقعیت نقطه را با فاصله از یک محور مرجع انتخابی (محور L در تصویر مقابل)، جهت از محور نسبت به یک جهت مرجع انتخابی (محور A) مشخص میکند. فاصله از صفحه مرجع انتخاب شده عمود بر محور (صفحه حاوی بخش بنفش). بسته به اینکه کدام طرف صفحه مرجع رو به نقطه است، فاصله اخیر به عنوان یک عدد مثبت یا منفی داده میشود. یک سیستم مختصات استوانهای با مبدا O، محور قطبی A و محور طولی L. نقطه نقطه با فاصله شعاعی ρ = ۴، مختصات زاویهای φ = 130 درجه و ارتفاع z = ۴ است. مبدأ سیستم نقطهای است که هر سه مختصات را میتوان صفر داد. این نقطه تقاطع بین صفحه مرجع و محور است. محور را بهطور متفاوتی محور استوانهای یا طولی مینامند تا آن را از محور قطبی متمایز کند، که پرتویی است که در صفحه مرجع قرار دارد و از مبدأ شروع میشود و در جهت مرجع قرار میگیرد. سایر جهات عمود بر محور طولی را خطوط شعاعی مینامند. فاصله از محور ممکن است فاصله شعاعی یا شعاع نامیده شود، در حالی که مختصات زاویهای گاهی اوقات به عنوان موقعیت زاویهای یا به عنوان آزیموت نامیده میشود. شعاع و آزیموت با هم مختصات قطبی نامیده میشوند، زیرا با یک سیستم مختصات قطبی دوبعدی در صفحه از طریق نقطه، موازی با صفحه مرجع مطابقت دارند. مختصات سوم ممکن است ارتفاع یا ارتفاع (اگر صفحه مرجع افقی در نظر گرفته شود)، موقعیت طولی، یا موقعیت محوری نامیده میشود. مختصات استوانهای در ارتباط با اجسام و پدیدههایی که دارای تقارن چرخشی حول محور طولی هستند، مانند جریان آب در یک لوله مستقیم با مقطع گرد، توزیع گرما در یک استوانه فلزی، میدانهای الکترومغناطیسی تولید شده توسط جریان الکتریکی در سیم بلند و مستقیم، قرصهای برافزایشی در نجوم و غیره. آنها گاهی اوقات «مختصات قطبی استوانهای» و «مختصات استوانهای قطبی» نامیده میشوند و گاهی برای تعیین موقعیت ستارگان در یک کهکشان («مختصات قطبی استوانهای کهکشانی مرکزی») استفاده میشوند.
منابع
[ویرایش]هندسه فضایی
هندسه مقدماتی
مکعب
مُکَعَّب (به انگلیسی: Cube) به حجم بسته سه بعدی گویند که از ۶ مربع برابر تشکیل شده باشد. به صورتی که هر ضلع هریک از مربعها با تنها یک مربع دیگر مشترک باشد و در رأسها سه مربع با یکدیگر در ارتباط هستند. مکعب را میتوان یک شش وجهی منظم نامید و یکی از پنج جسم افلاطونی است. اگر همه یا برخی از وجوه یک مکعب را از مربع به مستطیل تغییر بدهیم، شش وجهی به وجود آمده مکعب مستطیل نامیده میشود و اگر وجه های آن را به لوزی و متوازی الاضلاع تبدیل کنیم،به متوازی السطوح تبدیل می شود. گاه برای تمایز با مکعب مستطیل، مکعب (با وجوه مربع) را مکعب مربع نیز ممکن است بنامند.
مکعب درکل۲تا قاعده،۴تا وجه جانبی،۶تا وجه،۸تا راس و۱۲تا یال دارد.
حجم و مساحت
[ویرایش]حجم مکعب
[ویرایش]محاسبه حجم مکعب از طریق توان سوم اضلاع آن، توان سوم مکعب نامیده میشود همانطور که توان دوم مربع نامیده میشود.حجم آن به این صورت است:
محاسبه حجم مکعب به صورت مساحت چندضلعی منتظم
[ویرایش]مربع از نوع چندضلعی های منتظم است و از وجه های مکعب و قاعده مکعب مربع است.مساحت مربع همواره با فرمول مساحت چندضلعی برابر است.در اینجا:
مساحت
[ویرایش]مربع از نوع چندضلعی های منتظم است و از وجه های مکعب و قاعده مکعب مربع است.مساحت مربع همواره با فرمول مساحت چندضلعی برابر است.و مکعب از شش وجه مربع ساخته شده است و به همین از تشکیل وجه های چندضلعی منتظم،چندوجهی منتظم ساخته می شود.
مکعب نیز دارای مساخت کل نیز است.و مساحت آن برابر با این رابطه است:
اگر طبق مساحت چندضلعی حساب شود،به این صورت است.
در اینجا:
قضایا
[ویرایش]قضیه۲:حجم مکعب همراوه با توان سوم ضلع آن به همراه مساحت چندضلعی منتظم از طریق مربع برابر است.
مساحت مکعب نیز با مساحت چندضلعی ها به وجه های مربع که چهارضلعی منتظم است برابر است.
منابع
[ویرایش]ویکی پدیای فارسی
منشور
در هندسه ، منشور یک چندوجهی است که شامل یک پایه چند ضلعی n وجهی است ، یک پایه دوم که یک نسخه ترجمه شده (بدون چرخش بدون چرخش) است، و n وجه دیگر ، لزوماً همه متوازی الاضلاع ، که اضلاع متناظر دو پایه را به هم می پیوندند . . تمام مقاطع موازی با پایه ها ترجمه پایه ها هستند. منشورها بر اساس پایه هایشان نامگذاری می شوند، به عنوان مثال منشوری با پایه پنج ضلعی را منشور پنج ضلعی می نامند. منشورها زیرمجموعه ای از منشورها هستند.مانند بسیاری از اصطلاحات اولیه هندسی، کلمه منشور (از یونانی Prisma ( prisma ) "چیزی اره شده") برای اولین بار در عناصر اقلیدس استفاده شد . اقلیدس این اصطلاح را در کتاب یازدهم اینگونه تعریف کرد: «شکل جامدی که توسط دو صفحه متضاد، مساوی و موازی تشکیل شده است، در حالی که بقیه متوازی الاضلاع هستند». با این حال، این تعریف به دلیل مشخص نبودن کافی در رابطه با ماهیت پایه ها مورد انتقاد قرار گرفته است که باعث سردرگمی هندسه نویسان بعدی شد.
حجم و مساحت
[ویرایش]حجم
[ویرایش]حجم منشور اگرsمساحت قاعده و h ارتفاع باشد،حجم آن می شود:
مساحت
[ویرایش]مساحت جانبی منشور اگرpمحیط قاعده و hارتفاع باشد بر این اساس نوشته می شود.
مساحت کل منشور اگر s مساحت قاعده باشد می توان بر اساس این فرمول نوشت
حجم به صورت مثلثاتی
[ویرایش]حجم یک منشور حاصل ضرب مساحت قاعده و فاصله بین دو وجه قاعده یا ارتفاع است (در مورد منشور غیر راست توجه داشته باشید که این به معنای فاصله عمود بر هم است). که در آن B مساحت پایه و h ارتفاع است. حجم منشوری که قاعده آن یک چندضلعی منتظم n ضلعی با طول ضلع s است برابر است با:
مساحت به روش مثلثاتی
[ویرایش]مساحت سطح منشور راست 2 · B + P · h است که B مساحت قاعده، h ارتفاع و P محیط پایه است.
مساحت سطح یک منشور راست که قاعده آن یک چندضلعی n ضلعی منتظم با طول ضلع s و ارتفاع h است به این صورت است:
نسبت V/S منشور
[ویرایش]نسبت V/Sروشی است که نسبت حجم به سطح کل است
نسبتV/S منشور:
منابع
[ویرایش]ویکی پدیا فارسی
ویکی پدیای انگلیسی
استوانه

اُستوانه یا سُتوُن یکی از پایهایترین شکلهای منحنی فضایی در هندسه است که سطح دور آن را مجموعه نقاطی تشکیل میدهد که در فاصلهٔ یکسان از یک خط راست قرار دارند، این خط راست محور نام دارد. دو سر این شکل فضایی به کمک دو صفحهٔ عمود بر محور استوانه بسته میشود. سطح و حجم استوانه از گذشتههای دور برای ریاضیدانان معلوم بودهاست.
در هندسهٔ دیفرانسیل یک استوانه را به صورت یک سطح خطکشیده تعریف میکنند که مولد آن یک دسته خط موازی میباشد. استوانهای که مقطع عرضی آن یک بیضی، سهمی یا هذلولی باشد به ترتیب استوانهٔ بیضیگون، استوانهٔ سهمیگون و استوانهٔ هذلولیگون مینامند.
انواع
[ویرایش]سطح استوانه ای سطحی است متشکل از تمام نقاط روی تمام خطوط که موازی با یک خط معین هستند و از یک منحنی صفحه ثابت در صفحه ای غیر موازی با خط معین عبور می کنند. هر خطی در این خانواده از خطوط موازی، عنصر سطح استوانه ای نامیده می شود. از دیدگاه سینماتیک ، با توجه به یک منحنی مسطح به نام مستقیم ، سطح استوانهای به سطحی گفته میشود که توسط خطی به نام ژنراتیکس ترسیم میشود ، نه در صفحه مستقیم، که به موازات خود حرکت میکند و همیشه از مسیر مستقیم عبور میکند. . هر موقعیت خاص ژنراتیکس عنصری از سطح استوانه ای است.
یک استوانه دایره ای راست و مایل جامدی که توسط یک سطح استوانه ای و دو صفحه موازی محدود شده است، استوانه (جامد) نامیده می شود . قطعات خطی که توسط یک عنصر از سطح استوانه ای بین دو صفحه موازی تعیین می شود، عنصر استوانه نامیده می شود . تمام عناصر یک استوانه دارای طول مساوی هستند. ناحیه ای که توسط سطح استوانه ای در هر یک از صفحات موازی محدود شده است، قاعده استوانه نامیده می شود . دو قاعده یک استوانه شکلهای متجانس هستند. اگر عناصر استوانه بر صفحات حاوی پایه عمود باشند، استوانه یک استوانه راست است و در غیر این صورت استوانه مایل نامیده می شود . اگر پایه ها هستنددیسک ها (منطقه هایی که مرز آنها دایره است ) استوانه را استوانه دایره ای می نامند . در برخی از درمان های ابتدایی، استوانه همیشه به معنای استوانه مدور است.
ارتفاع یک استوانه فاصله عمودی بین پایه های آن است.استوانه ای که با چرخاندن یک پاره خط حول یک خط ثابت که موازی با آن است به دست می آید یک استوانه چرخشی است . استوانه چرخشی یک استوانه دایره ای راست است. ارتفاع یک سیلندر چرخشی طول قطعه خط تولید است. خطی که قطعه به دور آن می چرخد، محور استوانه نامیده می شود و از مرکز دو پایه می گذرد.
سیلندرهای دایره ای سمت راست
[ویرایش]اصطلاح سیلندر خالی اغلب به یک استوانه جامد با انتهای دایره ای عمود بر محور اشاره دارد، یعنی یک استوانه دایره ای راست، همانطور که در شکل نشان داده شده است. سطح استوانه ای بدون انتهای آن استوانه باز نامیده می شود . فرمول مساحت سطح و حجم استوانه دایره ای راست از دوران باستان شناخته شده است.
یک استوانه دایرهای راست را میتوان بهعنوان جامد چرخشی که با چرخاندن یک مستطیل به دور یکی از اضلاع آن ایجاد میشود، در نظر گرفت. این سیلندرها در یک تکنیک یکپارچه سازی ("روش دیسک") برای به دست آوردن حجم جامدات چرخشی استفاده می شوند.
حجم و مساحت
[ویرایش]حجم
[ویرایش]قاعده یک استوانه به صورت دایره ای است و نوعی منشور به حساب می آید.
- مساحت دایره(قاعده):
- ارتفاع:
- حجم استوانه:
حجم یک استوانه طبق حجم منشور ها حساب می گردد چون استوانه منشوری است و دوقاعده دارد و دارای ارتفاع نیز هست و قاعده آن نیز دایره ای است پس طبق حجم منشور می نویسیم
حجم استوانه به روش انتگرالی
[ویرایش]به طور کلی، بر اساس همین اصل، حجم هر استوانه حاصل ضرب مساحت پایه و ارتفاع است. به عنوان مثال، یک استوانه بیضوی با پایه دارای محور نیمه اصلی a ، محور نیمه فرعی b و ارتفاع h دارای حجم V = Ah است که در آن A مساحت بیضی پایه (= π ab ) است. این نتیجه برای استوانه های بیضوی راست را می توان با ادغام نیز به دست آورد، که در آن محور استوانه به عنوان محور x مثبت و A ( x ) = A مساحت هر مقطع بیضوی در نظر گرفته می شود، بنابراین:یک جزء از حجم، استوانهٔ راستی است که قاعدهٔ آن مساحتی برابر با Awi دارد و ضخامتی برابر با Δix دارد. پس اگر V حجم استوانهٔ دایرهای راست باشد، با استفاده از جمعهای ریمانی داریم:
با استفاده از مختصات استوانهای حجم را میتوان بوسیلهٔ انتگرالگیری بدست آورد:
مساحت
[ویرایش]با داشتن شعاع r و ارتفاع (ارتفاع) h ، سطح یک استوانه دایره ای سمت راست، به گونه ای که محور آن عمودی باشد، از سه قسمت تشکیل شده است:
- مساحت پایه بالایی:
- مساحت پایه پایین:
- مساحت ضلع:
مساحت پایه های بالا و پایین یکسان است و مساحت پایه B نامیده می شود . مساحت ضلع به نام ناحیه جانبی ، L شناخته می شود.
یک استوانه باز شامل عناصر بالا و پایین نیست و بنابراین دارای سطح (منطقه جانبی) است.
مساحت استوانه دایره ای راست جامد از مجموع هر سه جزء بالا، پایین و جانبی تشکیل شده است. بنابراین مساحت سطح آن،
که در آن d = 2 r قطر بالا یا پایین مدور است .
برای یک حجم معین، استوانه دایره ای سمت راست با کوچکترین سطح دارای h = 2 r است. به طور معادل، برای یک سطح معین، استوانه دایره ای سمت راست با بیشترین حجم دارای h = 2 r است، یعنی استوانه به خوبی در یک مکعب به طول ضلع = ارتفاع (= قطر دایره پایه) قرار می گیرد.
مساحت جانبی، L ، یک استوانه دایره ای، که نیازی به استوانه سمت راست نیست، به طور کلی به صورت زیر نشان داده می شود:
که e طول یک عنصر و p محیط قسمت سمت راست استوانه است. این فرمول قبلی را برای مساحت جانبی زمانی که استوانه یک استوانه دایره ای راست است، تولید می کند.
خواص
[ویرایش]مقاطع استوانه ای
[ویرایش]مقطع استوانه ای محل تلاقی سطح استوانه با یک صفحه است. آنها به طور کلی منحنی هستند و انواع خاصی از مقاطع صفحه هستند . مقطع استوانه ای توسط صفحه ای که شامل دو عنصر استوانه است متوازی الاضلاع است. چنین بخش استوانه ای از یک استوانه راست یک مستطیل است.
مقطع استوانه ای که در آن صفحه متقاطع قطع می شود و بر تمام عناصر استوانه عمود می شود، مقطع راست نامیده می شود . اگر قسمت سمت راست یک استوانه دایره ای باشد، استوانه یک استوانه دایره ای است. به طور کلی، اگر بخش راست استوانه یک مقطع مخروطی باشد (پارابولا، بیضی، هذلولی) استوانه جامد به ترتیب سهمی، بیضوی و هذلولی گفته می شود.
برای یک استوانه دایره ای راست، راه های مختلفی وجود دارد که هواپیماها می توانند با یک استوانه برخورد کنند. اول، صفحاتی که یک پایه را حداکثر در یک نقطه قطع می کنند. صفحه ای مماس بر استوانه است اگر در یک عنصر با استوانه برخورد کند. بخش های سمت راست دایره هستند و تمام صفحات دیگر سطح استوانه ای را به صورت بیضی قطع می کنند. اگر صفحه ای پایه استوانه را دقیقاً در دو نقطه قطع کند، پاره خطی که به این نقاط می پیوندد بخشی از بخش استوانه ای است. اگر چنین صفحه ای دارای دو عنصر باشد، یک مستطیل به عنوان بخش استوانه ای دارد، در غیر این صورت اضلاع بخش استوانه ای قسمت هایی از یک بیضی است. در نهایت، اگر صفحه ای بیش از دو نقطه از یک قاعده داشته باشد، کل قاعده را شامل می شود و قسمت استوانه ای یک دایره است.
در مورد یک استوانه دایره ای راست با مقطع استوانه ای که بیضی است، خروج از مرکز e بخش استوانه ای و محور نیمه اصلی a از بخش استوانه ای به شعاع استوانه r و زاویه α بین صفحه سکونت بستگی دارد. و محور سیلندر به روش زیر:
استوانه توخالی دایره ای راست (پوسته استوانه ای)
[ویرایش]یک استوانه توخالی دایره ای راست (یا پوسته استوانه ای ) ناحیه ای سه بعدی است که توسط دو استوانه دایره ای راست با محور یکسان و دو پایه حلقوی موازی عمود بر محور مشترک استوانه ها، مانند نمودار، محدود شده است.
بگذارید ارتفاع h ، شعاع داخلی r و شعاع خارجی R باشد. حجم داده شده توسطبنابراین، حجم یک پوسته استوانه ای برابر 2 π (شعاع متوسط) (ارتفاع) (ضخامت) است.
مساحت سطح، از جمله بالا و پایین، توسط داده می شود
پوستههای استوانهای در یک تکنیک ادغام رایج برای یافتن حجمهای جامد چرخشی استفاده میشوند.
محاط کره در استوانه
[ویرایش]در رساله به این نام نوشته شده ج. 225 قبل از میلاد، ارشمیدس به نتیجه ای دست یافت که بسیار به آن افتخار می کرد، یعنی به دست آوردن فرمول های حجم و سطح یک کره با بهره برداری از رابطه بین یک کره و استوانه دایره ای سمت راست آن با همان ارتفاع و قطر . حجم کره دو سوم حجم استوانه محدود شده و مساحت سطح دو سوم استوانه (شامل پایه ها) است. از آنجایی که مقادیر سیلندر قبلاً مشخص بود، او برای اولین بار مقادیر مربوط به کره را به دست آورد. حجم کره ای به شعاع r برابر با این رابطه است.طبق مساحت استوانه به ارتفاع و قطر برابر مساوی با این است که با ضرب دوسوم برابربااست.به درخواست او یک کره و استوانه حجاری شده بر روی مقبره ارشمیدس گذاشته شد.
معادله استوانه
[ویرایش]رابطهٔ استوانه مربوط به یک رویهٔ درجهٔ دوم است چون حداقل یکی از محورهای مختصات (در این مورد، محور zها) در آن ظاهر نشدهاست.
در یک استوانهٔ مایل قاعدههای بالا و پایین کمی نسبت به یکدیگر جابهجا شدهاند.
گونههای دیگری از استوانه وجود دارد که چندان معمول نیستند. این گونهها عبارتند از استوانههای بیضیگون پنداری:که در آن
و
و شعاع استوانهاست. معمولاً این نتیجهها با استفاده از ماتریسهای دوران بدست میآید.
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
کره
کره یک شی هندسی است که یک شبیه به یک دایره دو بعدی در سه بعدی است،کره مجموعه نقاطی از فضا است که به یک فاصله معین از یک نقطه به مرکز کره قرار دارد که به آن شعاع دایره گویند.شعاع کره مثل دایره برابر باrاست.کره از احجام هندسی است و از نوع اجسام کروی-چندوجهی به حساب می آید.

اصلاحات پایه
[ویرایش]شعاع کره را باRیاrنشان می دهند.شعاع کره از مرکز دایره تا نقطه ای نقاط کره امتداد دارد. اگر شعاع را از مرکز دایره کره به نقطه ای از کره که قاعده نصف کند امتداد دهیم قطر به وجود می آید.قطر دوبرابر شعاع است که با نماد2rیاdنشان می دهند.اگر شعاع کره برابر با عدد۱ باشد این کره یک واحد کره به حساب می آید.سیارات و ستاره ها و کره زمین و خورشید به صورت کروی هستند و از نوع کرات متشابه هستند.این اجرام آسمانی هم شعاع نیستند و به همین چون کره هستند باهم تشابه دارند. ریاضیدانان کره را یک سطح بسته دو بعدی می دانند که در فضای سه بعدی اقلیدسی جاسازی شده است . آنها یک کره و یک توپ را که یک منیفولد سه بعدی با مرزی است که شامل حجم موجود در کره است، متمایز می کنند. یک توپ باز خود کره را حذف می کند، در حالی که یک توپ بسته شامل کره است: یک توپ بسته ترکیب توپ باز و کره است و یک کره مرز یک توپ (بسته یا باز) است. تمایز بین توپ و کرههمیشه حفظ نشده است و به خصوص منابع ریاضی قدیمی تر در مورد کره به عنوان یک جامد صحبت می کنند. تمایز بین " دایره " و " دیسک " در هواپیما مشابه است.
کره های کوچک گاهی اوقات کروی نامیده می شوند، به عنوان مثال کره مریخ .
نکاتی درباره کره
[ویرایش]- حجم کره دوسوم حجم استوانه است
- مساحت آن چهار برابر مساحت دایره است
- کره نوعی چندوجهی است
- کره از نوع احجام هندسی است
- اگر حجم دو کره هم شعاع رد درهم ضرب کنیم حاصل برابر با چهار برابر حجم کره با شعاع مجذور دوکره است
- اگر مساحت دو کره هم شعاع رد درهم ضرب کنیم حاصل برابر با چهار برابر مساحت کره با شعاع مجذور دوکره است
- کره در مختصات سه بعدی به کار می رود
معادلات
[ویرایش]در هندسه تحلیلی کره ای با مرکز(x0,y0,z0)داشته باشیم و مختصات کره(x,y,z)برابر با مکان تمامی شعاع کره باشد. می توان آن را به صورت یک چند جمله ای درجه دوم بیان کرد، یک کره یک سطح چهارگانه ، نوعی سطح جبری است.
معادله فرض کنید a، b، c، d، e اعداد حقیقی با a ≠ 0 باشند و درمعادله درجه یک قرار دهیدسپس معادله برابر با
معادله پارامتریک
[ویرایش]اگر به صورت پارامپر معادله کره بدست آوریم به طوری که شعاع کره برابر باباشد و مرکز کره ما برابر باباشد به صورت زیر نوشته می گردد
نمادهای استفاده شده در اینجا همان نمادهایی است که در مختصات کروی استفاده می شود . r ثابت است، در حالی که θ از 0 تا π ومتغیر است از0 تا نیز متغیر است .
مداد کروی
[ویرایش]یک کره به طور منحصر به فرد توسط چهار نقطه که همسطح نیستند تعیین می شود. به طور کلی، یک کره به طور منحصر به فردی با چهار شرط مانند عبور از یک نقطه، مماس بودن بر صفحه و غیره تعیین می شود.این ویژگی مشابه این ویژگی است که سه نقطه غیر خطی یک دایره منحصر به فرد را در یک صفحه تعیین می کنند. در نتیجه، یک کره منحصراً توسط یک دایره و نقطه ای که در صفحه آن دایره نیست تعیین می شود (یعنی از آن عبور می کند). با بررسی راه حل های رایج معادلات دو کره می توان دریافت که دو کره در یک دایره قطع می شوند و صفحه حاوی آن دایره رادیکال نامیده می شود. صفحه ' کره های متقاطع. اگرچه صفحه رادیکال یک صفحه واقعی است، اما دایره ممکن است خیالی باشد (کره ها نقطه مشترک واقعی ندارند) یا از یک نقطه تشکیل شده باشد (کره ها در آن نقطه مماس هستند).اگر
f(x، y، z) = 0 و g( x، y، z) = 0
سپس معادلات دو کره مجزا هستند پس :
همچنین معادله یک کره برای مقادیر دلخواه پارامترهای λ و μ است. مجموعه تمام کرههایی که این معادله را برآورده میکنند «مداد کرهها» نامیده میشوند که توسط دو کره اصلی تعیین میشود. در این تعریف، کره مجاز است یک صفحه باشد (شعاع بی نهایت، مرکز در بی نهایت) و اگر هر دو کره اصلی صفحه باشند، تمام کره های مداد صفحه هستند، در غیر این صورت فقط یک صفحه (صفحه رادیکال) در آن وجود دارد. مداد.
حجم
[ویرایش]حجم کره بر اساس این رابطه نوشته می گردد. در این رابطه، r شعاع کره و π عدد پی است. این رابطه را نخستین بار ارشمیدس بدست آورد. او نشان داد که حجم یک کره ۲/۳ حجم استوانهٔ محیطی آن کرهاست. حجم کره بر اساس این رابطه نوشته می گردد.
اثبات حجم کره
[ویرایش]یک کره را در یک استوانه که قطر و ارتفاع آن برابر است محاط می کنیم. ابتدا کره را به دو نیم کره تقسیم میکنیم. اگر نیم کره را سه بار آب کنیم و در استوانه بریزیم حجم استوانه پر می شود.پس حجم نیمکره یک سوم حجم استوانه است و حجم کره دو سوم حجم استوانه است.

حجم استوانه=
اگر نسبت حجم کره به حجم استوانه را بر حجم استوانه ضرب کنیم حجم کره بدست می آید
که r شعاع و d قطر کره است. ارشمیدس ابتدا این فرمول را با نشان دادن اینکه حجم درون یک کره دو برابر حجم بین کره و استوانه محصور آن کره است (با ارتفاع و قطر برابر با قطر کره) به دست آورد. این را می توان با نوشتن یک مخروط به صورت وارونه در نیمکره ثابت کرد، با توجه به اینکه مساحت مقطع مخروط به اضافه سطح مقطع کره با سطح مقطع کره برابر است. استوانه محدود کننده، و استفاده از اصل کاوالیری . این فرمول همچنین می تواند با استفاده از حساب انتگرال نیز به دست آورد، یعنی ادغام دیسک برای مجموع حجم های بی نهایت از دیسک های دایره ای با ضخامت بی نهایت کوچک که در کنار هم چیده شده اند و در امتداد محور x از x = - r تا x = r متمرکز شده اند ، با فرض اینکه کره شعاع r در مرکز قرار گرفته است. اصل و نسب.
اثبات حجم کره به روش انتگرال ومثلثات
[ویرایش]نخست حجم نیم کره را بدست میآوریم و چون کره متقارن است حجم یک کرهٔ کامل دو برابر حجم نیم کره میشود. فرض کنید این کره از تعداد بی شماری دیسک دایرهای با ضخامت بسیار کم ساخته شدهاست. مجموع (انتگرال) حجم این دیسکها، حجم کرهٔ مورد نظر را میسازد. محور تمام این دیسکها بر روی محور yها قرار دارد در نتیجه دیسکی که بر روی نقطهٔ h = ۰ قرار دارد، شعاعی برابر با r دارد (s = r) و دیسکی که در نقطهٔ h = r قرار دارد، شعاعی برابر با صفر دارد (s = ۰).
اگر ضخامت دیسکها در هر نقطهٔ دلخواه h، برابر با δh باشد، آنگاه حجم دیسک برابر خواهد بود با مساحت مقطع دیسک در ضخامت آن:
پس حجم کل نیم کره برابر است با مجموع حجم دیسکها:
در بالای کره، شعاع دیسکها بسیار کوچک و نزدیک به صفر است. در نتیجه برای بدست آوردن مجموع حجم دیسکها باید از رابطهٔ بالا، انتگرال گرفت:
با توجه به قضیه فیثاغورس میدانیم که در هرنقطه بر روی محور عمودی داریم:
پس به جای از رابطهٔ زیر که تابعی از مقدار است استفاده میکنیم:
مقدار تازهٔ را در انتگرال جایگذاری میکنیم:
مقدار انتگرال برابر است با:
حجم نیمی از کره برابر با است پس حجم کل کره میشود:
حجم کره در دستگاه مختصات قطبی نیز قابل محاسبه است که در آن حالت باید از رابطهٔ زیر استفاده کرد:
بنابر این داریم
برای بیشتر اهداف عملی، حجم داخل یک کره حک شده در یک مکعب را می توان به 52.4٪ حجم مکعب تقریب زد، زیرا V =π/6 d 3 که d قطر کره و همچنین طول یک ضلع مکعب است وπ/6 ≈ 0.5236. به عنوان مثال، کره ای با قطر 1 متر، 52.4 درصد حجم یک مکعب با طول لبه 1 متر یا حدود 0.524 متر مکعب دارد.
بر اساس بازتابی از ریاضیدانان ارشمیدس یونانی، برای نیمکره ای با شعاع میدان مرجعی وجود دارد که حجم آن با نیمکره مطابقت دارد، اما محاسبه آسان است. این بدنه مقایسه با تبدیل یک استوانه (به طور دقیق تر: یک استوانه دایره ای راست) با شعاع سطح پایه و ارتفاع به a مخروط (به طور دقیق تر: مخروط دایره ای راست) با شعاع پایه و ارتفاع حذف شده است. فکر کنم نادرست باشد برای همین ادامه ندادم
می توان از اصل کاوالیری برای اثبات اینکه نیمکره و جسم مقایسه دارای حجم یکسانی هستند استفاده کرد. این اصل مبتنی بر ایده تقسیم اجسام در نظر گرفته شده به برش های بی نهایت با ضخامت بی نهایت کوچک (بی نهایت کوچک) است. (یک جایگزین برای این روش استفاده از حساب انتگرال خواهد بود.) با توجه به اصل ذکر شده، سطوح تقاطع هر دو جسم را با صفحه که موازی و یک فاصله از آن داده شده است. در مورد نیمکره، تقاطع یک ناحیه دایره ای است.
شعاع این ناحیه دایره ای از قضیه فیثاغورث حاصل می شود:
- .
این برای محتوای رابط می دهد
- .
از طرف دیگر، در مورد جسم مرجع، تقاطع یک حلقه دایره ای با شعاع بیرونی و یک شعاع داخلی است. مساحت این تقاطع بنابراین
- .
برای فاصله دلخواه تا ناحیه پایه، دو ناحیه تقاطع در محتوای ناحیه توافق دارند. این از اصل کاوالیری ناشی می شود که نیمکره و بدن مقایسه دارای حجم یکسانی هستند.
اکنون می توان حجم بدن مقایسه و در نتیجه نیمکره را به راحتی محاسبه کرد:
یکی کمتر از حجم استوانه و یکی بیشتر از حجم مخروط.
بنابراین، موارد زیر در مورد حجم کره (جامد) صدق می کند:
- .
اشتقاق جایگزین
[ویرایش]کره را می توان به بی نهایت هرم با ارتفاع (راس در مرکز کره) تقسیم کرد که قاعده کل آنها با سطح کره مطابقت دارد (به زیر مراجعه کنید). بنابراین حجم کل همه اهرام برابر است با:
.
استخراج با استفاده از حساب انتگرال
[ویرایش]شعاع در فاصله :
- .
ناحیه دایره ای در فاصله :
- .
حجم کره:
- .
حجم یک قطعه کروی از ارتفاع را می توان به همین ترتیب محاسبه کرد:
- .
مشتقات بیشتر
[ویرایش]کره ای با شعاع که مرکز آن در مبدا مختصات است، می تواند با معادله نمایش داده شود:
توضیح داده می شود که در آن مختصات فاصله هستند.
این مشکل را می توان به دو روش با استفاده از حساب انتگرال حل کرد:
ما کره را به یک مجموعه تهی لبسگو پارامتر بندی می کنیم.
با تعیین عملکردی:
عنصر حجم مورد نیاز به عنوان نتیجه میشود:
- .
بنابراین حجم کره به این صورت داده می شود:
امکان دیگر از طریق مختصات قطبی است:
اکنون دستگاه مختصات دکارتی به سیستم مختصات قطبی تبدیل می شود، به این معنی که ادغام پس از تغییر سیستم مختصات با استفاده از متغیرهای و به جای و . انگیزه این تحول، ساده سازی قابل توجه محاسبه در دوره بعدی است. برای دیفرانسیل این به این معنی است:
راه دیگر با کمک فرمول بدنه های انقلاب:
اگر قطعه ای از سطح را حول یک محور مکانی ثابت بچرخانید، جسمی با حجم معین به دست می آورید. در مورد یک ناحیه دایره ای، یک کره تشکیل می شود. این را می توان به عنوان یک سکه در حال چرخش تجسم کرد.
فرمول کلی برای چرخش بدن انقلاب حول محور x به دست میدهد:
- .
معادله به صورت دایره ای است:
با مرکز:
- .
با وصل کردن معادله دایره، دریافت می کنیم"
- .
با جایگزین کردن فرمول بدنه های چرخشی حول محور x، دریافت می کنیم:
مساحت
[ویرایش]مساحت کره از رابطهٔ زیر بدست میآید:
ارشمیدس نخستین کسی بود که توانست مساحت کره را بدست آورد. مشتق حجم کره نسبت به r، شعاع کره، مساحت کره را بدست میدهد. میتوان این گونه تصور کرد که حجم یک کره برابر است با مجموع مساحتهای بیشمار پوستهٔ کروی با ضخامت ناچیز که شعاع آنها از ۰ تا r میتواند متفاوت باشد. در نتیجه اگر هریک از جزء حجمهای کره را با δV، ضخامت هر پوسته را با δr و مساحت هر پوستهٔ کروی با شعاع r با(A(rنمایش دهیم؛ رابطهٔ زیر میان این متغیرها برقرار خواهد بود:
حجم کل برابر است با مجموع حجم هریک از این پوستهها:
هنگامی که δr به سمت صفر میل میکند باید از انتگرال بجای سیگما استفاده کنیم:
چون قبلاً فرمول حجم کره را بدست آوردهایم، پس خواهیم داشت:
از دو سر رابطهٔ بالا مشتق میگیریم:
که در حالت عمومی به صورت زیر نوشته میشود:
در دستگاه مختصات قطبی جزء سطح به صورت و در دستگاه مختصات دکارتی به صورت بدست میآید.
مساحت کل کره از انتگرال جزء سطح در تمام سطح کره بدست میآید:
کره دارای کمترین سطح در بین تمام سطوحی است که حجم معینی را در بر می گیرند و بیشترین حجم را در بین تمام سطوح بسته با یک سطح معین در بر می گیرد. بنابراین کره در طبیعت ظاهر می شود: برای مثال، حباب ها و قطرات کوچک آب تقریباً کروی هستند زیرا کشش سطحی به طور محلی سطح سطح را به حداقل می رساند.
مساحت سطح نسبت به جرم یک توپ را مساحت سطح مخصوص می نامند و می توان آن را از معادلات ذکر شده در بالا به صورت بیان کرد.
که ρ چگالی ( نسبت جرم به حجم) است.
روش دیگر
[ویرایش]سطح کره، سطح دو بعدی است که لبه کره را تشکیل می دهد. بنابراین مجموعه تمام نقاطی است که فاصله آنها از مرکز کره دارای مقدار ثابت است. این یک منیفولد دو بعدی بسته است. مساحت آن را همانطور که گفتیم برابر با است که این یعنی چهار برابر با مساحت دایره و دو سوم و همان مساحت سطح استوانه دایرهای است که کره را در بر می گیرد.برای یک حجم معین، کره کوچکترین سطح را در بین تمام اجسام ممکن دارد.
محاسبه مساحت
[ویرایش]
اگر یک کره را به زیر تقسیم کنید:
- لایه های هر کدام با ارتفاع باشد.
- طولی که در خط استوا نیز از هم فاصله دارند.
و اجازه دهید برای تلاش کند،
- بنابراین طول هر سلول برعکس متناسب با است—یعنی با فاصله آن از محور مرکزی.
- این از تصویر بالا در سمت راست مشخص است: فاصله نقطه مماس تا محور مرکزی است. مماس بر "سخن" عمود است و دو مثلث (راست) مشابه هستند. بر این اساس:
- .
- با این حال، عرض هر فیلد با متناسب است.
- این به طور مستقیم از نقاشی زیر، "نمای بالا" دنبال می شود.
بنابراین طول ضرب در عرض همیشه یکسان است، یعنی. همه میدان های مربع مساحت یکسانی دارند.
مساحت خط استوا است ( که در آن به تمایل دارد زیرا در خط استوا به سریعتر از به تمایل دارد. از آنجایی که همه فیلدها دارای محتوای هستند و در مجموع (تعداد فیلدها در جهت افقی ضربدر تعداد فیلدها در جهت عمودی، به عنوان مثال) وجود دارد در آنجا فیلد میشود مساحت کل همه فیلدها است: .
مشتق جایگزین با استفاده از حجم کره
[ویرایش]کره ای را می توان متشکل از بی نهایت بی نهایت کوچک (بی نهایت کوچک) هرم تصور کرد. پایه های این اهرام با هم سطح کره را تشکیل می دهند. ارتفاع اهرام برابر با شعاع کره است. از آنجایی که حجم هرم با فرمول داده میشود، یک رابطه متناظر با حجم کل همه هرمها، یعنی حجم کره اعمال میشود:
- (
بر اساس پیدا کردن حجم کره به صورت مساحت کره برابر با:
مشتق جایگزین با استفاده از حجم یک کره و حساب دیفرانسیل
[ویرایش]حجم کره بر اساس این فرمولتعریف میشود و از سوی دیگر، سطح با توجه به تغییر حجم تعریف می شود:
این است که فرمول سطح بلافاصله از مشتق فرمول حجم پیروی می کند.
استخراج با استفاده از حساب انتگرال
[ویرایش]به صورت انتگرالی اینگونه بدست می آید
برای سطح جانبی بدنه چرخشی:
استخراج با استفاده از حساب انتگرال در مختصات کروی
[ویرایش]برای عنصر سطح روی سطوح = ثابت در مختصات کروی اعمال می شود:
- .
این امر محاسبه سطح را آسان می کند:
خواص
[ویرایش]یک کره را می توان به عنوان سطحی که با چرخاندن یک دایره به دور هر یک از قطرهای آن تشکیل می شود، ساخت . این اساساً تعریف سنتی کره است که در عناصر اقلیدس ارائه شده است . از آنجایی که دایره نوع خاصی از بیضی است، کره نیز نوع خاصی از بیضوی چرخش است. با جایگزینی دایره با یک بیضی که حول محور اصلی آن چرخیده است ، شکل به یک کروی پرولات تبدیل می شود . چرخش حول محور فرعی، یک کروی مایل.
یک کره به طور منحصر به فرد توسط چهار نقطه که همسطح نیستند تعیین می شود. بهطور کلیتر، یک کره به طور منحصربهفردی چهار شرط مانند عبور از یک نقطه، مماس بودن بر صفحه و غیره تعیین میشود .
در نتیجه، یک کره منحصراً توسط یک دایره و نقطه ای که در صفحه آن دایره نیست تعیین می شود (یعنی از آن عبور می کند).
با بررسی جواب های رایج معادلات دو کره ، می توان دریافت که دو کره در یک دایره همدیگر را قطع می کنند و صفحه حاوی آن دایره، صفحه رادیکال کره های متقاطع نامیده می شود. اگرچه صفحه رادیکال یک صفحه واقعی است، اما دایره ممکن است خیالی باشد (کره ها نقطه مشترک واقعی ندارند) یا از یک نقطه تشکیل شده باشد (کره ها در آن نقطه مماس هستند).
زاویه بین دو کره در یک نقطه تقاطع واقعی، زاویه دو وجهی است که توسط صفحات مماس بر کره در آن نقطه تعیین می شود. دو کره در تمام نقاط دایره تقاطع خود با یک زاویه قطع می شوند. آنها در زوایای قائمه متقاطع می شوند ( متعامد هستند ) اگر و فقط در صورتی که مجذور فاصله بین مراکز آنها برابر با مجموع مربعات شعاع آنها باشد.
یازده خواص کره
[ویرایش]این خواص را دو ریاضی دان اروپایی به اسم دیوید هیلبرت و استفان کوهن ووسن در کتاب هندسه خود توصیف کرده اند و این خواص های اثبات شده است.
- نقاط روی کره همگی از یک نقطه ثابت فاصله دارند. همچنین نسبت فاصله نقاط آن از دو نقطه ثابت ثابت است.
- بخش اول تعریف معمول کره است و آن را به طور منحصر به فرد تعیین می کند. قسمت دوم به راحتی قابل استنباط است و نتیجه مشابه آپولونیوس پرگا برای دایره را دنبال می کند. این قسمت دوم نیز برای هواپیما صادق است.
- خطوط و مقاطع صفحه کره دایره هستند.
- این ویژگی کره را به طور منحصر به فردی تعریف می کند.
- کره دارای عرض ثابت و دور ثابت است.
- عرض یک سطح فاصله بین جفت صفحات مماس موازی است. بسیاری از سطوح محدب بسته دیگر دارای عرض ثابت هستند، به عنوان مثال بدنه مایسنر . دور یک سطح، محیط مرز برآمدگی متعامد آن روی یک صفحه است. هر یک از این ویژگی ها بر دیگری دلالت دارد.
- تمام نقاط یک کره ناف هستند .
- در هر نقطه از سطح یک جهت عادی با سطح زوایای قائمه است زیرا در کره این خطوط هستند که از مرکز کره خارج می شوند. تقاطع صفحه ای که دارای حالت عادی با سطح است منحنی را تشکیل می دهد که به آن مقطع نرمال می گویند و انحنای این منحنی انحنای نرمال است . برای اکثر نقاط روی بیشتر سطوح، بخش های مختلف انحناهای متفاوتی دارند. مقادیر حداکثر و حداقل آنها را انحنای اصلی می نامند . هر سطح بسته حداقل چهار نقطه به نام نقاط نافی دارد. در یک ناف تمام انحناهای مقطعی برابر هستند. به ویژه انحناهای اصلیبرابر هستند. نقاط ناف را می توان به عنوان نقاطی در نظر گرفت که سطح آن با یک کره تقریباً نزدیک است.
- برای کره، انحنای تمام بخش های عادی برابر است، بنابراین هر نقطه یک ناف است. کره و صفحه تنها سطوحی هستند که این خاصیت را دارند.
- کره سطحی از مراکز ندارد.
- برای یک مقطع عادی، دایره ای از انحنا وجود دارد که برابر با انحنای مقطع است، مماس بر سطح است، و خطوط مرکزی آن در امتداد خط عادی قرار دارند. به عنوان مثال، دو مرکز مربوط به حداکثر و حداقل انحنای مقطع ، نقاط کانونی نامیده می شوند و مجموعه تمام این مراکز، سطح کانونی را تشکیل می دهند.
- برای اکثر سطوح، سطح کانونی دو صفحه تشکیل می دهد که هر کدام یک سطح هستند و در نقاط ناف به هم می رسند. چند مورد خاص هستند:
- * برای سطوح کانال یک ورق یک منحنی و ورق دیگر یک سطح است
- * برای مخروط ها ، استوانه ها، توری ها و سیکلیدها ، هر دو ورق منحنی تشکیل می دهند.
- * برای کره، مرکز هر دایره منعشکننده در مرکز کره است و سطح کانونی یک نقطه واحد را تشکیل میدهد. این خاصیت منحصر به کره است.
- تمام ژئودزیک های کره منحنی های بسته هستند.
- ژئودزیک ها منحنی هایی روی سطحی هستند که کمترین فاصله را بین دو نقطه نشان می دهند. آنها تعمیم مفهوم خط مستقیم در صفحه هستند. برای کره، ژئودزیک ها دایره های بزرگی هستند. بسیاری از سطوح دیگر این ویژگی را به اشتراک می گذارند.
- از میان تمام جامداتی که حجم معینی دارند، کره با کمترین مساحت سطحی است. از بین تمام جامداتی که سطح مشخصی دارند، کره بیشترین حجم را دارد.
- از نابرابری ایزوپریمتری نتیجه می شود . این ویژگیها کره را بهطور منحصربهفردی تعریف میکنند و میتوان آن را در حبابهای صابون مشاهده کرد : حباب صابون یک حجم ثابت را در بر میگیرد و کشش سطحی سطح آن را برای آن حجم به حداقل میرساند. بنابراین یک حباب صابون شناور آزادانه به یک کره نزدیک می شود (اگرچه نیروهای خارجی مانند گرانش شکل حباب را کمی تغییر می دهد). همچنین در سیارات و ستارگانی که گرانش سطح اجرام آسمانی بزرگ را به حداقل می رساند، دیده می شود.
- کره کوچکترین انحنای میانگین کل را در بین تمام جامدات محدب با سطح معین دارد.
- انحنای متوسط میانگین دو انحنای اصلی است که ثابت است زیرا دو انحنای اصلی در تمام نقاط کره ثابت هستند.
- کره دارای انحنای متوسط ثابت است.
- کره تنها سطح نهفته است که فاقد مرز یا تکینگی با میانگین انحنای مثبت ثابت است. سایر سطوح غوطه ور مانند سطوح حداقل دارای میانگین انحنای ثابت هستند.
- کره دارای انحنای گاوسی مثبت ثابت است.
- انحنای گاوسی حاصلضرب دو انحنای اصلی است. این یک ویژگی ذاتی است که می توان آن را با اندازه گیری طول و زوایا تعیین کرد و مستقل از نحوه قرار گرفتن سطح در فضا است. از این رو، خمش یک سطح، انحنای گاوسی را تغییر نمیدهد و سایر سطوح با انحنای گاوسی مثبت ثابت را میتوان با بریدن یک شکاف کوچک در کره و خم کردن آن به دست آورد. همه این سطوح دیگر دارای مرز خواهند بود و کره تنها سطحی است که فاقد مرزی با انحنای گاوسی ثابت و مثبت است. شبه کره نمونه ای از سطحی با انحنای گاوسی منفی ثابت است.
- کره توسط یک خانواده سه پارامتری از حرکات صلب به خود تبدیل می شود.
- چرخش حول هر محوری یک کره واحد در مبدأ، کره را روی خودش ترسیم می کند. هر چرخشی حول یک خط از مبدا می تواند به صورت ترکیبی از چرخش ها حول محور سه مختصات بیان شود (به زوایای اویلر مراجعه کنید ). بنابراین، یک خانواده سه پارامتری از چرخش ها وجود دارد به طوری که هر چرخش کره را به خود تبدیل می کند. این خانواده گروه چرخشی SO(3) است. صفحه تنها سطح دیگری است که دارای یک خانواده تبدیل سه پارامتری است (ترجمه در امتداد محورهای x - و y و چرخش حول مبدا). استوانه های دایره ای تنها سطوح با خانواده های دو پارامتری از حرکات صلب و سطوح چرخشی و هلیکوئیدی هستند.تنها سطوح با خانواده یک پارامتری هستند.
درمان بر اساس حوزه ریاضیات
[ویرایش]هندسه کروی
[ویرایش]عناصر اساسی هندسه صفحه اقلیدسی نقاط و خطوط هستند . در کره، نقاط به معنای معمول تعریف می شوند. آنالوگ "خط" ژئودزیک است که یک دایره بزرگ است . مشخصه تعیین کننده یک دایره بزرگ این است که صفحه ای که تمام نقاط آن را در بر می گیرد از مرکز کره نیز عبور می کند. اندازهگیری با طول قوس نشان میدهد که کوتاهترین مسیر بین دو نقطه قرار گرفته روی کره، بخش کوتاهتر دایره بزرگ است که نقاط را شامل میشود.
بسیاری از قضایای هندسه کلاسیک برای هندسه کروی نیز صادق است، اما همه اینها صادق نیستند، زیرا کره نمی تواند برخی از فرضیه های هندسه کلاسیک ، از جمله فرض موازی را برآورده کند . در مثلثات کروی ، زاویه ها بین دایره های بزرگ تعریف می شوند. مثلثات کروی از بسیاری جهات با مثلثات معمولی متفاوت است . به عنوان مثال، مجموع زوایای داخلی یک مثلث کروی همیشه از 180 درجه بیشتر است. همچنین، هر دو مثلث کروی مشابه همخوان هستند.
هر جفت نقطه روی یک کره که روی یک خط مستقیم از مرکز کره (یعنی قطر) قرار می گیرد، نقاط پادپای نامیده می شوند - روی کره، فاصله بین آنها دقیقاً نصف طول محیط است. هر جفت نقطه متمایز دیگری (یعنی نه پادپا) روی یک کره
- روی یک دایره بزرگ بی نظیر دراز بکش،
- آن را به یک قوس مینور (یعنی کوتاهتر) و یک قوس اصلی (یعنی بلندتر) تقسیم کنید و
- طول قوس فرعی کمترین فاصله بین آنها روی کره باشد.
هندسه کروی شکلی از هندسه بیضوی است که همراه با هندسه هذلولی هندسه غیر اقلیدسی را تشکیل می دهد.
هندسه دیفرانسیل
[ویرایش]کره یک سطح صاف با انحنای گاوسی ثابت در هر نقطه برابر با 1/ r2 است. طبق نظریه گاوس، این انحنا مستقل از جاسازی کره در فضای 3 بعدی است. همچنین با پیروی از گاوس، یک کره را نمی توان با حفظ هر دو ناحیه و زوایا به صفحه نگاشت کرد. بنابراین، هر طرح ریزی نقشه نوعی اعوجاج را معرفی می کند.
کره ای به شعاع r دارای عنصر مساحت است . این را می توان از عنصر حجم در مختصات کروی با r ثابت یافت.
کره ای با هر شعاع با مرکز صفر، سطحی جدایی ناپذیر از شکل دیفرانسیل زیر است :
این معادله نشان می دهد که بردار موقعیت و صفحه مماس در یک نقطه همیشه متعامد با یکدیگر هستند. علاوه بر این، بردار معمولی رو به بیرون برابر با بردار موقعیت است که با 1/r مقیاس شده است.
در هندسه ریمانی ، حدس ناحیه پر شدن بیان می کند که نیمکره پر شدن ایزومتریک بهینه (کمترین مساحت) دایره ریمانی است .
منحنی روی یک کره
[ویرایش]منحنی دایره ای(حلقه ای)
[ویرایش]دایرههای روی کره مانند دایرههایی در صفحه هستند که از تمام نقاط با فاصله معینی از یک نقطه ثابت روی کره تشکیل شدهاند. محل تقاطع یک کره و یک صفحه یک دایره، یک نقطه یا خالی است. دایره های بزرگ محل تلاقی کره با صفحه ای است که از مرکز یک کره می گذرد: بقیه دایره های کوچک نامیده می شوند.
سطوح پیچیده تر نیز ممکن است یک کره را به صورت دایره ای قطع کنند: تقاطع یک کره با سطح چرخشی که محور آن شامل مرکز کره است (هم محور هستند ) از دایره ها و/یا نقاط اگر خالی نباشند تشکیل شده است. به عنوان مثال، نمودار سمت راست تقاطع یک کره و یک استوانه را نشان می دهد که از دو دایره تشکیل شده است. اگر شعاع استوانه شعاع کره باشد، تقاطع یک دایره واحد خواهد بود. اگر شعاع استوانه بزرگتر از شعاع کره بود، تقاطع خالی بود.
لوکسودروم
[ویرایش]در ناوبری ، خط رومب یا لوکسودروم کمانی است که از تمام نصف النهارهای طول جغرافیایی در یک زاویه عبور می کند. لوکسودروم همان خطوط مستقیم در طرح مرکاتور است . خط لوزی یک مارپیچ کروی نیست . به جز برخی موارد ساده، فرمول خط روم پیچیده است.
منحنی کلیا
[ویرایش]منحنی کللیا منحنی روی کره ای است که طول جغرافیایی آن استو همبستگیمعادله را برآورده کند
موارد خاص عبارتند از: منحنی ویویانی () و مارپیچ های کروی () مانند مارپیچ سیفرت . منحنی های کلیا مسیر ماهواره ها را در مدار قطبی تقریبی می کند .
مخروط های کروی
[ویرایش]آنالوگ یک مقطع مخروطی روی کره یک مخروطی کروی است ، یک منحنی کوارتیک که می تواند به چندین روش معادل تعریف شود، از جمله:
- به عنوان محل تلاقی یک کره با یک مخروط درجه دوم که راس آن مرکز کره است.
- به عنوان تقاطع یک کره با یک استوانه بیضوی یا هذلولی که محور آن از مرکز کره می گذرد.
- به عنوان مکان نقاطی که مجموع یا اختلاف فواصل دایره بزرگ از یک جفت کانون ثابت است.
بسیاری از قضایای مربوط به مقاطع مخروطی مسطح به مخروط های کروی نیز گسترش می یابد.
تقاطع یک کره با سطح عمومی تر
[ویرایش]اگر یک کره با سطح دیگری قطع شود، ممکن است منحنی های کروی پیچیده تری وجود داشته باشد.
مثال
[ویرایش]تقاطع کره - استوانه
تقاطع کره با معادلهو استوانه با معادلهفقط یک یا دو دایره نیست. حل سیستم غیر خطی معادلات است
تاریخ
[ویرایش]هندسه کره توسط یونانیان مورد مطالعه قرار گرفت. عناصر اقلیدس کره را در کتاب XI تعریف میکند، در کتاب دوازدهم ویژگیهای مختلف کره را مورد بحث قرار میدهد و نشان میدهد که چگونه پنج چند وجهی منظم را در یک کره در کتاب سیزدهم حک کنید. اقلیدس مساحت و حجم یک کره را در بر نمی گیرد، فقط یک قضیه را شامل می شود که حجم یک کره به عنوان توان سوم قطر آن تغییر می کند، احتمالاً به دلیل Eudoxus of Cnidus . فرمول های حجم و مساحت ابتدا در کتاب ارشمیدس روی کره و استوانه با روش اگزوز تعیین شد. زنودوروس اولین کسی بود که بیان کرد، برای یک سطح معین، کره جامد با حداکثر حجم است.
ارشمیدس در مورد مشکل تقسیم یک کره به بخش هایی نوشت که حجم آنها در یک نسبت مشخص است، اما آن را حل نکرد. راه حلی با استفاده از سهمی و هذلولی توسط دیونیسودوروس آمیسوس (حدود قرن اول پیش از میلاد) ارائه شد و مسئله مشابهی - ساختن قطعه ای برابر حجم با یک قطعه معین و از نظر سطح با یک قطعه دیگر - بعداً حل شد. توسط القیحی .
نگارخانه
[ویرایش]

منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
هرم
هرم شکلی سهبعدی است کهاز اتصال نقطهای درفضا به تمام نقاط شکلی بسته در صفحه به وجود میآید. به آن نقطه، رأس هرم و به آن شکل مسطح، قاعده هرم گفته میشود. قاعده هرم، چندضلعی دلخواه است و سایر وجهها مثلثهایی همرس هستند که در رأس به یکدیگر متصل میشوند. خط قائمی که رأس را به قاعده متصل میکند، ارتفاع هرم نامیده میشود. از معروف ترین سازه های جهان به شکل هرم ،می توان به اهرام ثلاثه مصر اشاره کرد.
هشت قانون برای هرم
[ویرایش]- هر هرم دارای یک راس مرکزی است
- حجم آن ثلث حجم منشور است
- هرمی که آن دایره است مخروط نام دارد
- وجه های هرم مثلثی است
- هرم دارای یال است
- چندوجهی هرمی چهاروجهی و هشت وجهی است
- هشت وجهی دارای دوهرم است
- برای محاسبه ارتفاع هرم از رابطه فیثاغورس استفاده می کنیم.
اهرام راست منظم و نامنظم
[ویرایش]منظم
[ویرایش]هرم راست با قاعده منتظم دارای اضلاع مثلث متساوی الساقین است که تقارن آنها C n v یا [1, n ] و با مرتبه 2 n است. می توان یک نماد Schläfli توسعه یافته∨ {n}، نشان دهنده یک نقطه(n)، متصل (متعامد افست) به یک چند ضلعی منظم ، {n} به آن داد. عملیات اتصال یک لبه جدید بین تمام جفت رئوس دو شکل به هم پیوسته ایجاد می کند.
هرم مثلثی یا مثلثی با تمام وجوه مثلث متساوی الاضلاع تبدیل به چهار وجهی منظم می شود که یکی از جامدات افلاطونی است. مورد تقارن پایین هرم مثلثی C 3v است که دارای یک قاعده مثلث متساوی الاضلاع و 3 ضلع مثلث متساوی الساقین یکسان است. هرم های مربع و پنج ضلعی نیز می توانند از چند ضلعی های محدب منظم تشکیل شده باشند که در این صورت آنها جامدات جانسون هستند .
اگر تمام لبه های هرم مربعی (یا هر چند وجهی محدب) مماس بر یک کره باشند به طوری که میانگین موقعیت نقاط مماسی در مرکز کره باشد، آنگاه به هرم گفته می شود که متعارف است و نیمی از یک کره را تشکیل می دهد. هشت وجهی منظم .
اهرام با پایه شش ضلعی یا بالاتر باید از مثلث های متساوی الساقین تشکیل شده باشند. یک هرم شش ضلعی با مثلث های متساوی الاضلاع یک شکل کاملاً مسطح است و اگر هفت ضلعی یا بالاتر باشد، مثلث ها اصلاً به هم نمی رسند.
نامنظم
[ویرایش]هرم سمت راست را می توان به صورت∨P نام برد که در آن نقطه راس، ∨ عملگر اتصال و P چند ضلعی پایه است.
چهار ضلعی قائم الزاویه متساوی الساقین را می توان به صورت[(n)∨(n)∨{n}] به عنوان اتصال یک نقطه به یک قاعده مثلث متساوی الساقین ، به صورت [(n)∨(b)∨{n)یا {n}∨{n} به عنوان پیوستن (تغییرهای متعامد) دو بخش متعامد، یک دیسپنوئید دو ضلعی ، حاوی 4 وجه مثلث متساوی الساقین. دارای تقارن C1v از دو جهت مختلف پایه-راس، و C2v در تقارن کامل آن است.
یک هرم راست مستطیل شکل که به صورت
[(n}∨{n}×(n}] نوشته می شود
یک هرم لوزی شکل به صورت (n}∨{n}]+{n}]، هر دو دارای تقارن C2v هستند.
حجم و مساحت
[ویرایش]حجم
[ویرایش]حجم یک هرم (همچنین هر مخروطی) است، کهS مساحت قاعده و h ارتفاع از قاعده تا راس است. این برای هر چند ضلعی، منتظم یا غیرمنظم، و هر مکان راس کار می کند، مشروط بر اینکه h به عنوان فاصله عمود از صفحه حاوی قاعده اندازه گیری شود.
فرمول را می توان به طور رسمی با استفاده از حساب دیفرانسیل و انتگرال اثبات کرد. با تشابه، ابعاد خطی یک مقطع موازی با پایه به صورت خطی از راس به پایه افزایش می یابد. ضریب مقیاس (ضریب تناسب) است، یا، که در آن h ارتفاع و y فاصله عمود از صفحه پایه تا سطح مقطع است. از آنجایی که مساحت هر مقطع با مربع ضریب پوسته پوسته شدن شکل متناسب است ، مساحت سطح مقطع در ارتفاع y برابر است بایا از آنجایی که b و h یاهر دو ثابت هستند و دو عبارتوداریم. حجم توسط انتگرال داده می شود
همین معادله،همچنین برای مخروط ها با هر پایه نگه می دارد. این را می توان با استدلالی مشابه استدلال فوق اثبات کرد; حجم یک مخروط را ببینید .
به عنوان مثال، حجم هرمی که قاعده آن یک چندضلعی منتظم n ضلعی با طول ضلع s و ارتفاع آن h است.
این فرمول را می توان دقیقاً بدون حساب برای اهرام با پایه های مستطیلی نیز به دست آورد. یک مکعب واحد را در نظر بگیرید. از مرکز مکعب به هر یک از 8 راس خطوط بکشید. این مکعب را به 6 هرم مربع مساوی با سطح پایه 1 و ارتفاع 1/2 تقسیم می کند. حجم هر هرم به وضوح 1/6 است. از این نتیجه می گیریم که حجم هرم =
(3/ارتفاع × مساحت پایه)
در مرحله بعد، مکعب را به طور یکنواخت در سه جهت به مقدار نامساوی باز کنید تا لبه های مستطیلی مستطیل شکل a , b و c با حجم جامد abc باشند. هر یک از 6 هرم داخل نیز به همین ترتیب گسترش یافته اند. و هر هرم دارای همان حجم abc /6 است. از آنجایی که جفت اهرام دارای ارتفاع های a /2، b /2 و c /2 هستند، می بینیم که حجم هرم = ارتفاع × مساحت پایه / 3 دوباره.
وقتی مثلث های ضلعی متساوی الاضلاع باشند، فرمول حجم به این صورت است
این فرمول فقط برای n = 2، 3، 4 و 5 اعمال می شود. و همچنین مورد n = 6 را پوشش می دهد که حجم آن برابر با صفر است (یعنی ارتفاع هرم صفر است).
مساحت
[ویرایش]مساحت یک هرم برابر با این رابطه است.
Pیعنی محیط چندضلعی و Bیعنی مساحت قاعده هرم است.
Lکمان هرم است و فرمول آن بر اساس این رابطه نوشته می گردد
اگر قاعده هرم چندضلعی باشد بر اساس این رابطه نوشته می گردد
anیعنی Pو محیط چندضلعی است.
اهرام nبعدی
[ویرایش]هرم 2 بعدی مثلثی است که توسط یک لبه قاعده متصل به یک نقطه غیرخطی به نام راس تشکیل شده است.
هرم 4 بعدی هرم چند وجهی نامیده می شود که توسط یک چند وجهی در یک ابر صفحه 3 فضایی 4 فضایی با یک نقطه دیگر از آن ابرصفحه ساخته شده است.
اهرام با ابعاد بالاتر به طور مشابه ساخته می شوند.
خانواده ساده ها هرم ها را در هر بعد نشان می دهند که از مثلث ، چهار وجهی ، 5 سلولی ، 5 ساده و غیره افزایش می یابند. یک سیمپلکس n بعدی دارای حداقل n+1 رئوس است، با تمام جفت رئوس به هم متصل شده توسط یال ها ، همه سه برابر هستند. از رئوس که چهره ها را مشخص می کنند، تمام نقاط چهارگانه تعیین کننده سلول های چهار وجهی و غیره.
اهرام چندوجهی منتظم
[ویرایش]در هندسه 4 بعدی ، هرم چند وجهی یک پلی توپ 4 است که توسط یک سلول چند وجهی پایه و یک نقطه راس ساخته شده است. وجوه جانبی سلول های هرمی هستند که هر کدام توسط یک وجه از چندوجهی پایه و راس ساخته شده اند. رئوس و لبههای اهرام چند وجهی نمونههایی از گرافهای راس را تشکیل میدهند، نمودارهایی که با افزودن یک راس (راس) به یک نمودار مسطح (نمودار پایه) شکل میگیرند.
5 سلولی معمولی (یا 4 - سیمپلکس ) نمونه ای از هرم چهار وجهی است. چندوجهی یکنواخت با دورنماهای کمتر از 1 را می توان هرم های چند وجهی با اضلاع چهاروجهی منظم ساخت. یک چندوجهی با رئوس v ، یالهای e و وجههای f میتواند پایه یک هرم چند وجهی با راسهای v+1 ، یالهای e+v ، وجههای f+e و سلولهای 1+f باشد .
یک هرم چند وجهی 4 بعدی با تقارن محوری را می توان به صورت سه بعدی با نمودار شلگل - یک برآمدگی سه بعدی که راس را در مرکز چند وجهی پایه قرار می دهد، تجسم کرد.
هر 4-پلی توپ محدب را می توان با اضافه کردن یک نقطه داخلی و ایجاد یک هرم از هر وجه به نقطه مرکزی به اهرام چند وجهی تقسیم کرد. این می تواند برای محاسبه حجم ها مفید باشد.
ابرحجم 4 بعدی یک هرم چند وجهی 1/4 حجم چند وجهی پایه ضربدر ارتفاع عمود آن است، در مقایسه با مساحت یک مثلث که 1/2 طول قاعده ضربدر ارتفاع و حجم هرم است. 1/3 مساحت پایه ضربدر ارتفاع.
حجم سطح سه بعدی هرم چند وجهی است،
جایی که B حجم پایه، A مساحت سطح پایه، و L ارتفاع مایل(ارتفاع سلول های هرمی جانبی) است که بر این روش بیان می شود.
که در آن h ارتفاع و r شعاع است.
منابع
[ویرایش]ویکی پدیای انگلیسی
ویکی پدیای فارسی
مخروط
یک مخروط یک شکل هندسی سهبُعدی است که از پایهٔ تختش (سطح مقطع مخروط) به آرامی یا به سرعت (به سطح قاعده و ارتفاع بستگی دارد) تا راس باریک میشود. بهطور جزئیتر شکلی جامد است که به یک صفحهٔ پایه (سطح مقطع مخروط)، محدود میشود و سطح جانبی آن نیز مکان هندسی خطوط راستی است که نوک مخروط را به نقاط پیرامون پایه (سطح مقطع) پیوند میزنند. واژهٔ مخروط گاهی به رویهٔ این جسم توپر گفته میشود و گاه تنها به رویهٔ پهلویی آن.
مخروطها میتوانند به صورت قائم یا اریب باشند. لازم است ذکر شود که حجم یک مخروط اریب با مساحت سطح مقطع معین و ارتفاع مشخص، با حجم یک مخروط قائم با همان مساحت و ارتفاع معین، برابر است.
تعریف ها و تعمیم ها
[ویرایش]یک مخروط توسط مجموعه ای از پاره های خط ، نیم خط یا خطوطی تشکیل می شود که یک نقطه مشترک، راس، را به همه نقاط روی یک پایه که در صفحه ای است که راس را شامل نمی شود، متصل می کند. بسته به نویسنده، پایه ممکن است به یک دایره ، هر شکل درجه دوم یک بعدی در صفحه، هر شکل یک بعدی بسته ، یا هر یک از موارد بالا به اضافه تمام نقاط محصور محدود شود. اگر نقاط محصور در پایه قرار گیرند، مخروط یک جسم جامد است . در غیر این صورت دو بعدی استجسم در فضای سه بعدی در مورد یک جسم جامد، مرز تشکیل شده توسط این خطوط یا خطوط جزئی، سطح جانبی نامیده می شود . اگر سطح جانبی نامحدود باشد، سطح مخروطی است .
در مورد پاره های خط، مخروط فراتر از قاعده گسترش نمی یابد، در حالی که در مورد نیمه خطوط، تا بی نهایت فاصله دارد. در مورد خطوط، مخروط در هر دو جهت از راس بی نهایت امتداد دارد، در این صورت گاهی اوقات آن را مخروط دوتایی می نامند.. هر یک از نیمی از مخروط دوتایی در یک طرف راس، ناپ نامیده می شود .
محور یک مخروط ، خط مستقیمی است (در صورت وجود)، که از راس عبور می کند، که قاعده (و کل مخروط) در اطراف آن دارای تقارن دایره ای است .
در استفاده متداول در هندسه ابتدایی ، مخروط ها را دایره راست فرض می کنند ، که در آن دایره به معنای دایره است و راست به این معنی است که محور از مرکز پایه در زوایای قائم به صفحه خود می گذرد. اگر مخروط دایره ای راست باشد، تقاطع یک صفحه با سطح جانبی یک مقطع مخروطی است. با این حال، به طور کلی، پایه ممکن است به هر شکلی باشد و راس ممکن است در هر جایی قرار داشته باشد (اگرچه معمولاً فرض میشود که پایه محدود است و بنابراین دارای مساحت محدودی است.، و اینکه راس خارج از صفحه قاعده قرار دارد). در تقابل با مخروطهای راست، مخروطهای مورب هستند که در آنها محور بهطور غیر عمود از مرکز قاعده عبور میکند.
مخروط با قاعده چند ضلعی هرم نامیده می شود .
بسته به زمینه، "مخروط" ممکن است به طور خاص به معنای مخروط محدب یا مخروط برجسته نیز باشد.
حجم و مساحت
[ویرایش]حجم
[ویرایش]حجم یک هرم برابر بر این رابطه است که چون سه هرم برابر با حجم منشور است.پس حجم هرم برابر با این رابطه است.
حجم یک مخروط چون قاعده آن دایره است،به این صورت نوشته می گردد.
در ریاضیات مدرن، این فرمول را می توان به راحتی با استفاده از حساب دیفرانسیل و انتگرال محاسبه کرد - تا مقیاس بندی، انتگرال است.
بدون استفاده از حساب دیفرانسیل و انتگرال، فرمول را می توان با مقایسه مخروط با یک هرم و اعمال اصل کاوالیری - به ویژه، مقایسه مخروط با یک هرم مربع راست (مقیاس عمودی)، که یک سوم مکعب را تشکیل می دهد، اثبات کرد. این فرمول را نمیتوان بدون استفاده از چنین استدلالهای بینهایتی اثبات کرد - بر خلاف فرمولهای دو بعدی برای مساحت چند وجهی، اگرچه شبیه به مساحت دایره است - و از این رو قبل از ظهور حساب دیفرانسیل و انتگرال، اثباتهای کمتر دقیقتری را پذیرفتند، با یونانیان باستان از روش استفاده میکردند. فرسودگی . این اساساً محتوای مسئله سوم هیلبرت است - به طور دقیق تر، همه اهرام چند وجهی با قیچی همخوانی ندارند.(می توان آن را به قطعات متناهی تقسیم کرد و به قطعات دیگر مرتب کرد) و بنابراین حجم را نمی توان صرفاً با استفاده از یک آرگومان تجزیه محاسبه کرد
مساحت
[ویرایش]مساحت جانبی یک مخروط بر اساس مساحت هرم برابر با این تساوی است.
rشعاع مخروط وLکمان مخروط است
ارتفاع اصلی مخروط دایره ای راست، فاصله ای از هر نقطه از دایره قاعده آن تا راس از طریق یک قطعه خط در امتداد سطح مخروط است. توسط آن داده می شود، جایی کهrشعاع پایه است وhارتفاع است این را می توان با قضیه فیثاغورث ثابت کرد.
مساحت کل مخروط بر اساس این رابطه نوشته می گردد.
مساحت کل یعنی مساحت قاعده به علاوه مساحت جانبی
محاسبه کمان مخروط و دور مخروط
[ویرایش]اگرrشعاع وhارتفاع باشد.دور و کمان مخروط برابر با این رابطه است.
اگرcدور و Lکمان مخروط باشد،مساحت اینگونه است.
براساس زاویه و ارتفاع راس مساحت مخروط برابر با این رابطه است
فرم معادلات
[ویرایش]سطح یک مخروط را می توان به صورت پارامتربندی کرد
جایی که زاویه تتا برابر باو زاویه اطراف مخروط است و ارتفاع جزئی از اعداد حقیقی باشد یعنیاست.
مخروط دایره ای جامد راست با ارتفاعhو دیافراگم، که محور آن استzمحور مختصات و راس آن مبدا است، به صورت پارامتریک به عنوان توصیف می شود
جایی کهu,t,s محدوه بیش از، به ترتیب در شکل ضمنی ، همان جامد با نابرابری ها تعریف می شود.
جایی که به طور کلی، یک مخروط دایره ای راست با راس در مبدا، محور موازی با بردار d و دیافراگم، توسط معادله برداری ضمنی به دست می آیدجایی که
یا
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
قطاع کروی
در هندسه،"قطاع کروی"، که به عنوان "مخروط کروی" نیز شناخته می شود، بخشی از یک کره یا یک توپ توسط یک مرز مخروطی با راس در مرکز کره تعریف شده است. می توان آن را به عنوان اتحاد یک عرقچین و مخروط که توسط مرکز کره و پایه کلاهک تشکیل شده است توصیف کرد. این آنالوگ سه بعدی بخش یک دایره است.

حجم
[ویرایش]اگر شعاع کره را با r و ارتفاع کلاهک را با h نشان دهیم، حجم بخش کروی است:
ممکن است این نیز به صورت نوشته شود :
جایی که φ نصف زاویه مخروط است، یعنی، φ زاویه بین لبه کلاهک و جهت به وسط کلاهک است که از تصویر مشاهده می شود. مرکز کره حجم V بخش مربوط به ناحیه A کلاهک است:
مساحت
[ویرایش]منحنی سطح بخش کروی (روی سطح کره، به استثنای سطح مخروط) است. : هم هست : که در آن Ω زاویه جامد بخش کروی در استرادیان ثانیه است، واحد SI زاویه جامد. یک استرادیان به عنوان زاویه ثابتی تعریف میشود که توسط ناحیه کلاهکی A = r2 فروکش میکند.
اشتقاقات دیفرانسیل
[ویرایش]حجم را می توان با ادغام المان حجم دیفرانسیل محاسبه کرد. : بیش از حجم بخش کروی اینگونه است: جایی که انتگرال ها از هم جدا شده اند، زیرا انتگرال را می توان به حاصلضرب توابع با یک متغیر ساختگی جدا کرد. مساحت را می توان به طور مشابه با ادغام عنصر مساحت کروی دیفرانسیل محاسبه کرد : بیش از بخش کروی، دادن : که در آن "φ" تمایل (یا ارتفاع) و "θ" سمت راست (راست) است. توجه کنید "r" یک ثابت است. باز هم انتگرال ها
فرمول های عمیق تر
[ویرایش]فرمول های زیر برای محاسبه حجم، مساحت جانبی و سطح یک مقطع از یک کره اعمال می شود. تعیین شده استR شعاع کره،a شعاع دایره پایه قطعه کروی و h ارتفاع قطعه کروی این سه کمیت مستقل از یکدیگر نیستند. بخش کروی با هر دو از این سه کمیت تعیین می شود. سومی را می توان از دو مقدار از سه مقدار محاسبه کرد. در همه فرمول ها، اگر مقطع کروی کمتر از نصف کره باشد، − برای ± در نظر گرفته می شود، در غیر این صورت + برای ±.
به جایوتعیین زاویه نیز کافی استدایره پایه (به تصویر مراجعه کنید). موارد زیر اعمال می شود:
بنابراین، بسته به اینکه کدام یک از مقادیر داده شده است، چندین فرمول در هر مورد وجود دارد.
| فرمولاسیون های عمومی قطاع کروی | |
|---|---|
| مساحت سطح جانبی مخروط | |
| مساحت سطح جانبی بخش کروی | |
| مساحت سطح | |
موارد خاص
[ویرایش]برای ، و بخش کروی یک نیمکره است: برای ، و بخش کره یک کره کامل است:
اشتقاق
[ویرایش]برای استخراج این فرمول، آن را به دو جسم تقسیم میکنیم: مخروط و قطعه کروی. این مخروط دارای شعاع پایه و ارتفاع است. حجم مخروط است : قطعه کروی دارای حجم است : حجم بخش کروی نیز همینطور است : از قضیه فیثاغورث ما بدست می آوریم. درج و حذف براکت ها در نهایت ارائه می شود : روش دیگر برای محاسبه حجم مختصات کروی است:
که در آن نصف زاویه دیافراگم قسمت مخروط است. با فرمول بالا برای volume به شرح زیر است. سطح مخروط است :
و سطح قسمت کره است (به استثنای دایره پایه). : .
پس این سطح است : ج
منابع
[ویرایش]https://en.m.wikipedia.org/wiki/Spherical_sector
https://de.m.wikipedia.org/wiki/Kugelausschnitt
چهاروجهی منتظم
چهاروجهی منتظم،یک جسم هندسی است که از چهار تا مثلث متساوی الاضلاع است و از خانواده چندوجهی ها است و جزء اجسام افلاطونی است. چهاروجهی دارای یک راس مرکز،5راس ودارای 6راس،3وجه است و یک قاعده است.در احجام هندسی اگر یک جسم هندسی یک قاعده و راس مرکزی داشته باشد،این جسم هرمی است.پس چهاروجهی یک جسم هرمی است.می توان این نتیجه را گرفت که چهاروجهی یک جسم هرمی-چندوجهی-افلاطونی است.چهاروجهی تنها شکلی نیست که از وجه های مثلث متساوی الاضلاع داشته باشد.بیست وجهی منتظم نیز دارای وجه های مثلث متساوی الاضلاع است.

تشکیل و شکل فیزیکی چهاروجهی
[ویرایش]با بههم رسیدن سه سهضلعی منتظم (مثلث متساویالاضلاع) در هر رأس، چهاروجهی منتظم تشکیل میشود. مجموع زوایا در هر رأس برابر ۳ × ۶۰° = ۱۸۰° میشود که از ۳۶۰° کمتر است، بنابراین چهاروجهی منتظم جسم افلاطونی است. اگر هریک از لیگاندها در روی هر چهار گوشه یک چهار وجهی قرار گیرد و اتم مرکزی وسط چهار وجهی قرار گیرد شکل کمپلکس چهار وجهی است.
چهاروجهی منتظم با خودش مزدوج است. یعنی با وصل کردن نقطهٔ وسط وجههای آن یک چهاروجهی کوچکتر میتوان ساخت (تعداد وجوه و رئوس چهاروجهی با هم برابر است). افلاطون و فیثاغوریها باور داشتند که چهاروجهی منتظم، که نوکهای تیز دارد، ساختاردهندهٔ عنصر آتش در هستی است.کپلر باور داشت که چهاروجهی منتظم مبین فاصلهٔ بین مشتری و مریخ در منظومه شمسی است.
مجموع زاویه های چهاروجهی برابر با°۷۲۰درجه است.
حجم
[ویرایش]پیدا کردن مساحت قاعده و ارتفاع چهاروجهی
[ویرایش]مساحت قاعده
[ویرایش]برای پیدا کردن حجم چهاروجهی به مساحت قاعده نیاز است که قاعده آن به شکل مثلث متساوی الاضلاع است. پس مساحت مثلث متساوی الاضلاع را بدست می آوریم.
ابتدا ارتفاع قاعده را به روش فیثاغورس بدست می آوریم
در اینجا مثلث را به دو مثلث قائم الزاویه تبدیل می کنیم و ضلع قاعده نصف می شود و به همین دلیل نصف قاعده ضلع مجاور و ضلعaوتر است وhارتفاع است.
ارتفاع اینگونه بدست می آید
مساحت قاعده به این صورا بیان می گردد
ارتفاع
[ویرایش]برای محاسبه حجم به ارتفاع نیز لازم است. و ارتفاع بر این اساس نوشته می گردد.
حجم
[ویرایش]با توجه به این که مساحت قاعده و ارتفاع را داریم اینگونه می نویسیم.
مساحت
[ویرایش]مساحت چندوجهی اینگونه است که مساحت چهاروجه چهاروجهی را محاسبه می کنیم.
مساحت مثلث متساوی الساقین اینگونه است.
پس مساحت چهاروجهی برابر با این رابطه است.
رابطه مساحت چهاروجهی با چندضلعی منتظم
[ویرایش]مثلث متساوی الاضلاع از خانواده چندضلعی های منتظم است.پس طبق مساحت چندضلعی اینگونه می نویسیم.
اگر کسر سه چهارم را در کتانژانت پی/nام ضرب کنیم برابر با ربع رادیکال عدد سه می شود.
مساحت چهاروجهی طبق مساحت چندضلعی برابر با این رابطه است.
منابع
[ویرایش]چندضلعی منتظم
مساحت و حجم
ویکی پدیای فارسی
متوازی السطوح
در هندسه ، متوازی السطوح یک شکل سه بعدی است که توسط شش متوازی الاضلاع تشکیل شده است (اصطلاح لوزی نیز گاهی با این معنی استفاده می شود). بر اساس قیاس، به متوازی الاضلاع مربوط می شود همانطور که یک مکعب به یک مربع مربوط می شود. در هندسه اقلیدسی ، چهار مفهوم - متوازی السطوح و مکعب در سه بعدی، متوازی الاضلاع و مربع در دو بعد - تعریف شده است، اما در زمینه یک هندسه وابسته کلی تر ، که در آن زوایا متمایز نمی شوند، فقط متوازی الاضلاع هستند.و متوازی السطوح وجود دارد. سه تعریف معادل از موازی شکل هستند.متوازی السطوح نیز جز احجام هندسی است و از نوع چندوجهی ها است ولی از نوع منتظم نمی باشد.
خواص
[ویرایش]- هر یک از سه جفت وجه موازی را می توان به عنوان صفحات پایه منشور مشاهده کرد. یک متوازی الاضلاع دارای سه مجموعه از چهار یال موازی است. لبه های هر مجموعه دارای طول مساوی هستند.
- متوازی الاضلاع از تبدیل های خطی یک مکعب (برای موارد غیر انحطاط: تبدیل خطی دوطرفه) حاصل می شود.
- از آنجایی که هر وجه دارای تقارن نقطه ای است , متوازی الاضلاع یک زونهدرون است . همچنین کل متوازی الاضلاع دارای تقارن نقطه ای C i است. هر صورت، از بیرون، تصویر آینه ای از چهره مقابل است. صورت ها به طور کلی کایرال هستند ، اما موازی شکل نیست.
- با رونوشتهای همخوان از هر موازیپایهای امکانپذیر است که فضا را پر کند.
- اگر همه ضلع های مکعب را به یک زاویه برابر مورب کنیم به یک متوازی السطوح تبدیل می شود که تمام وجه هایش لوزی است و مساحت وجه های متوازی السطوح با با مساحت وجه های مکعب برابر است.
- متوازی السطوح از انواع منشورها است
- متوازی السطوح را می توان یکی از چندوجهی ها گفت
رابطه
[ویرایش]چهار وجهی مربوطه
[ویرایش]حجم هر چهار وجهی که دارای سه یال همگرای متوازی الاضلاع است، حجمی برابر با یک ششم حجم آن متوازی الاضلاع دارد.
رابطه متوازی السطوح با مکعب
[ویرایش]حجم یک متوازی السطوح با ضلع های مساوی با مکعب باهم برابر اند.همچنین مساحت های آن دو نیز برابر است.
حجم
[ویرایش]متوازی السطوح حجمی است که از سه بردار سه بعدی a,b,cدرست شده است و با ضرب خارجی بردار ها درست شده است.
محاسبه حجم
[ویرایش]ابتدا متوازی السطوحی رسم می کنیم که در فضای برداری باشد و در فضای سه بعدیR3قرار می دهیم.بردار های آن اینگونه است که:
محاسبه حجم اینگونه است مساحت قاعده بر اساس مساحت متوازی الاضلاع بدست آید و ارتفاع آن بر اساس رابطه فیثاغورس بدست آید.پس حجم متوازی السطوح برابر با این رابطه است.
کسینوس تتا و سینوس تتا در محاسبه قدر مطلق برابر با یک می شود،قدرمطلق مساحت برداری هایa,b,cبرابر با خودشان است.
می توان به روش عمیق تری حجم آن را بدست آورد،ضرب داخلی بردار های خارجی که با ضرب خارجی این سه بردار متوازی السطوح را بدست آورند این گونه است.حجم برابر است
که همان برابر با این رابطه است.راه دیگر برای اثبات ( V1 ) استفاده از مولفه اسکالر در جهت استa×b
از بردار:a,b,c
حجم متوازی السطوح به صورت مختصاتی برابر با این عبارت فوق است اما به روش دیگر هم که به صورا مختصاتی نوشته نمی گردد بلکه مثل حجم مکعب مستطیل است که برابر با ضرب طول بردار هاست ولی یک عبارتی لازم دارد. نتیجه بر این است.
با استفاده از روش قدر مطلق و محاسبه ضرب داخلی و خارجی بردارها به مقداری به نامkنیاز است.kمقداری است که بر اساس زاویه های لبه متوازی السطوح بدست می آید.که به صورت جذر آن درحجم متوازی السطوح به کار می رود.
مقدار kبراساس این رابطه بدست می آید.مقدار جذر آن این گونه است
حجم آن براساس این رابطه نوشته می گردد.که می توان این گونه نوشتکه برابر با حجم مختصاتی متوازی السطوح است.
مساحت
[ویرایش]مساحت یک متوازی السطوح براساس جمع مساحت شش متوازی الاضلاع بدست می آید که براساس این رابطه نوشته می گرددمساحت متوازی السطوح مثل مساحت مکعب مستطیل بدست می آید،مکعب،مکعب مستطیل از احجام منشوری است که به صورت برداری کشیده اند.
به صورت دیگر هم مساحت آن پیدا می گردد که به صورت مساحت متوازی الاضلاع بدست می آید
برای پیدا کردن مساحت متوازی السطوج بر اساس a,b,c اینگونه است.
hبرابر با ارتفاع متوازی السطوح است بر حسب تتا زاویه است که h بر اساس رابطه فیثاغورس نوشته میشود.
=مقداری است که بر اساس تتا زیر جزئی از طول های به ترتیب b,c است
اگر این دو رابطه را محاسبه کنیم به این نتیجه می رسیم
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
چندوجهی
چندوجهی یک شیء صلب هندسی در فضای سه بعدی است که وجههایی صاف و منظم(هر وجه در یک صفحه) و ضلعها یا یالهایی واقع بر خط راست دارد. تا کنون تعریف واحدی برای آن ارائه نشدهاست. چهاروجهی از انواع هرم است و مکعب نمونهای از یک شش وجهی است. چندوجهی میتواند محدب یا غیر محدب باشد.چندوجهیهایی مثل هرم و منشور را با میتوان اکستروژن (بیرون کشیدن) چندضلعیهای دوبعدی ساخت. تنها تعداد محدودی از چندوجهیهای محدب با وجوه منتظم و شکل گوشههای برابر میتواند وجود داشته باشد که شامل اجسام افلاطونی و اجسام ارشمیدسی میشود. برخی اجسام ارشمیدسی را میتوان با بریدن هرم راس اجسام افلاطونی ساخت.به دلیل سادگی ساختن، در غالب آثار معماری مانند گنبدهای ژئودزیک و اهرام از چندوجهیها استفاده میشود. اخیراً نیز به علت استفاده از اشکال علاقه به سطوح چندوجهی افزایش یافتهاست. برخی مولکولها و اتمهای فشرده، بهویژه ساختارهای بلوری و هیدروکربنهای افلاطونی و همچنین برخی شعاعیان شکلی شبیه اجسام افلاطونی دارند. از اجسام افلاطونی در ساخت تاس نیز استفاده میشود.چندوجهیها ویژگیها و انواع گوناگونی دارند و در گروههای تقارنی مختلفی جای میگیرند. با اعمالی روی هر چندوجهی میتوان چندوجهیهای دیگری ساخت. بعضی از آنها با هم روابطی دارند. چندوجهیها از عصر حجر مورد توجه بودهاند.کره نیز از خانواده چندوجهی ها نیز به حساب می آید.مکعب،چهاروجهی،متوازی السطوح از احجام های هندسی هستند که چندوجهی نیز به حساب می آید.
تعریف ها
[ویرایش]چندوجهی های محدب تعریف شده اند و خود چندوجهی های محدب نیز خوش تعریف و قابل محاسبه حجم و مساحت هستند و می توان جز احجام هندسی به کار برد. اما چندوجهی های مقعر جز احجام غیر هندسی هستند و تعریف آنها سخت و خیلی سخت است و فرمول مساحت و حجم ثابت نیز ندارند.احجام هندسی و غیرهندسی از نوع چندوجهی ها هستند ولی تفاوت آنها در مقعر و محدب بودن آنها است.
از این تعاریف میتوان به موارد زیر اشاره کرد:
- یک تعریف متداول و تا حدودی ساده از چند وجهی این است: شیء جامدی که سطوح بیرونی آن را میتوان با تعداد زیادی وجه پوشش داد یا اینکه یک جامد است که به صورت اتحاد چندوجهیهای محدب شکل گرفتهاست. ارتقاء طبیعی این تعریف مستلزم این است که جامد مورد بحث کراندار بوده، فضای داخلی آن و احتمالاً مرز آن نیز همبند باشند. وجوه چنین چندوجهی ای را میتوان به عنوان فضای همبند قسمتهای مرز درون هر یک از صفحاتی که آن را پوشاندهاند، و ضلعها و رئوس آنها را به عنوان بخشهای خط و نقاطی که وجوه در آنها به هم میرسند، تعریف کرد. با این حال، چندوجهی تعریف شده به این روش شامل چندوجهیهای ستاره ای متقاطع نیست که ممکن است وجوه آن را چندضلعیهای ساده تشکیل ندهند و برخی از ضلعهای آن متعلق به بیش از دو وجه باشد.
- تعاریف مبتنی بر ایده سطح محدود کننده و نه جامد نیز معمول است. به عنوان مثال، اورورک (۱۹۹۳) چندوجهی را به عنوان اجتماع چندضلعیهای محدب (وجوه آن) تعریف میکند. این چند ضلعیها به گونهای در فضا آرایش یافتهاند که تقاطع (یا اشتراک) هر دو چندضلعی یک راس یا ضلع مشترک یا مجموعه تهی است، به طوری که اجتماعشان یک منیفلد است. اگر یک قسمت مسطح از چنین رویهای خود چندضلعی محدبی نباشد، اورورک این شرط را میگذارد که آن قسمت باید به قطعاتی تقسیمبندی شوند که هر کدام چندضلعیهای محدب کوچکتری بوده به گونهای که زوایای دووجهی بینشان تخت باشند. تا حدودی بهطور کلی تر، برانکو گرونباوم یک چندوجهی را به عنوان مجموعهای از چندضلعیهای ساده تعریف میکند که یک منیفلد تعبیه شده را تشکیل میدهند، با هر راس که حداقل سه ضلع به آن میرسد و هر دو وجه فقط در راسها و ضلعهای مشترک هر یک از هم تلاقی میکنند. کتاب چندوجهیهای کرامول تعریف مشابهی ارائه میدهد اما بدون محدودیت حداقل سه ضلع در هر راس. باز هم، این نوع تعریف شامل چندوجهیهای متقاطع نیست مفاهیم مشابه اساس تعاریف توپولوژیک از چند وجهی را تشکیل میدهند، به عنوان زیرمجموعههای یک منیفلد توپولوژیکی به دیسکهای توپولوژیک (وجهها) که تقاطعهای دوتایی آنها به صورت نقطه (رئوس)، قوسهای توپولوژیکی (ضلعها) یا مجموعه تهی است. با این حال، چندوجهی توپولوژیکی (حتی با مثلثهای تمام وجه) وجود دارد که نمیتوان آنها را به عنوان چند وجهی هندسی درک کرد.
- تعریف مدرن تری مبتنی بر نظریه چندوجهیهای مجرد نیز رواج دارد. این چندوجهیها را میتوان به صورت مجموعههایی با ترتیب جزئی تعریف نمود، به گونه ای که عناصر آنها راسها، ضلعها و وجههای یک چند وجهی هستند. هنگامی که راس یا ضلع کوچکتر از ضلع یا وجه باشد، یک عنصر راس یا ضلع کمتر از عنصر ضلع یا وجه است (به این ترتیب جزئی). علاوه بر این، ممکن است یکی از عناصر زیرین ویژه این ترتیب جزئی (نشان دهنده مجموعه تهی) و یک عنصر بالا نشان دهنده کل چندوجهی باشد. اگر بخشهای ترتیب جزئی بین عناصر سه وجه از هم فاصله داشته باشند (یعنی بین هر وجه و عنصر پایین و بین عنصر بالا و هر راس) ساختار مشابه نمایش انتزاعی یک چند ضلعی را دارند، سپس این مجموعههایی که مرتب شدهاند دقیقاً همان اطلاعات را با چند وجهی توپولوژیکی حمل میکنند. با این حال، این الزامات اغلب سهل گیرانه هستند، در عوض فقط به این نیاز است که مقاطع بین عناصر دو وجه از یکدیگر دارای ساختار مشابه نمایش انتزاعی یک بخش خط باشند. (این بدان معنی است که هر ضلع شامل دو رأس است و به دو وجه تعلق دارد و هر رأس در یک وجه به دو ضلع آن وجه تعلق دارد) چند وجهی هندسی، که به روشهای دیگر تعریف شدهاست، میتواند به صورت انتزاعی از این طریق توصیف شود، اما همچنین میتوان از چندوجهی انتزاعی به عنوان اساس تعریف چندوجهی هندسی استفاده کرد. تحقق یک چندوجهی انتزاعی بهطور کلی به عنوان نگاشتی از رئوس چندوجهی انتزاعی به نقاط هندسی در نظر گرفته میشود، بدین ترتیب که نقاط هر وجه به صورت همسطح است. پس میتوان یک چندوجهی هندسی را به عنوان تحقق چندوجهی انتزاعی تعریف کرد. تحققاتی که الزام مسطح بودن را حذف میکنند، الزامات اضافی تقارن را تحمیل کرده یا رئوس را به فضاهای ابعاد بالاتر مینگارند نیز در نظر گرفته شدهاند. تعریف اخیر، برخلاف تعاریفی که بر مبنای جامدات و رویهها ارائه شدهاند، برای چندوجهی ستاره ای کاملاً مناسب میباشد. با این حال، بدون محدودیتهای اضافی، این تعریف اجازه میدهد تا چندوجهی تبهگن یا بیوفا (به عنوان مثال، با نگاشت تمام رئوس در یک نقطه واحد) ساخت و این سؤال که: «چگونه تحقق بخشی از اینها را محدود کنیم تا از این تبهگنیها جلوگیری شود؟» نیز لاینحل باقی ماندهاست.
در همه این تعاریف، یک چندوجهی به عنوان یک نمونه سه بعدی از پلیتوپ کلی تر در هر تعداد ابعاد قابل درک است. به عنوان مثال، یک چندضلعی جسمی دو بعدی دارد و هیچ وجهی ندارد، در حالی که یک چهار پلیتوپ دارای یک بدنه چهار بعدی و یک مجموعه اضافی از «سلول» های سه بعدی است. با این حال، برخی از متون مربوط به هندسه ابعاد بالاتر از اصطلاح «چندوجهی» برای معنای دیگری استفاده میکنند: نه یک پلیتوپ سه بعدی، بلکه شکلی است که به نوعی با یک پلیتوپ متفاوت است. به عنوان مثال، برخی منابع چندضلعی محدب را به عنوان محل تلاقی بسیاری از نیم فضاها و یک پلیتوپ را به صورت چندوجهی کراندار تعریف میکنند. در این مقاله تنها به چندوجهی ۳ بعدی پرداخته شدهاست.
زاویا
[ویرایش]- زاویه مسطحه:به هر کدام از زوایای گوشه وجوه چندضلعیهای چندوجهی زاویه مسطحه گویند.
- زاویه فضایی:به هر کدام از زوایایی که چندوجهی در فضای سه بعدی روی رأس میپوشاند زاویه فضایی گویند. هر کدام از این زوایا با سه یا بیشتر از ۳ زاویه زاویه صاف محصور شدهاند.
- زاویه دووجهی:به هر کدام از زوایایی که بین دو وجه چندوجهی پدید آیند، زاویه دووجهی گویند.
سطح چندوجهی
[ویرایش]«سطح چندوجهی» حاصل بههم پیوستن تعداد محدودی وجه چندضلعی تخت است و ملزوما فضایی را محصور نمیکند. در سطوح چندوجهی میتوان اضلاع مرزی و رئوس مرزی (تنها در زمانی که سطح چندوجهی شامل فقط یک وجه باشد) داشت.
اخیراً به علت استفاده از اشکال علاقه به سطوح چندوجهی در معماری افزایش یافتهاست.
مقدمات
[ویرایش]منظور از مقدمات،موارد جزئی است که به صورا ساده تعریف می کنیم.
وجه
[ویرایش]در چندوجهیها، وجه (به انگلیسی: Face) هر يك از چندضلعی هاى داراى مساحت۱ است که بخشی از مرز یک جسم جامد را تشکیل می دهد. یک جامد سه بعدی که منحصراً توسط وجوه محدود شده است یک چندوجهی است.
در روشهای فنیتر هندسه چند وجهیها و پلیتوپهای با ابعاد بالاتر ، این اصطلاح همچنین به معنای عنصری از هر بعد از یک پلیتوپ عمومیتر (در هر تعداد ابعاد) استفاده میشود.
راس
[ویرایش]رَأس (به عربی: رأس) (به انگلیسی: vertex) در هندسه، نقطهای است که دو پهلوی مستقیم از یک چندضلعی باز یا بسته به هم میرسند. به زبان دیگر، رأس، نوکِ گوشهها یا برخوردگاههای خطوط یک شکل هندسی است. از پیوند دادن دو رأس به همدیگر یک خط و از پیوند دادن سه رأس به هم یک سطح پدید میآید.
در مدلهای سهبعدی گرافیک رایانهای از رأسها معمولاً برای تعریف سطوح (معمولاً سهگوشها) استفاده میشود و هر یک از رأسها در این مدلها به عنوان یک بُردار نشان داده میشود. در نظریه گراف رأس را گره نیز مینامند.
تعداد رئوس هر چندضلعی در صفحه برابر تعداد اضلاع آن است.
ضلع
[ویرایش]در هندسه، ضِلع یا بَر یا لَبه پارهخطی است که دو رأس مجاور را در یک چندضلعی به هم پیوند دهد؛ بنابراین در عمل، یک ضلع رابطی برای یک پارهخط یکبعدی و دو شی صفر بعدی است.
ضلع به خطهای سازنده هر شکل گویند که اغلب تعداد آنها در هر شکل نسبت به اشکال دیگر متفاوت است.برای نمونه مثلث، ۳ ضلع و مربع و مستطیل ۴ ضلع دارند.
توالیِ بستهٔ مسطح از ضلعها، یک چندضلعی (و یک وجه) را شکل میدهد. در یک چندوجهی، در هر ضلع دقیقاً دو وجه با یکدیگر تماس دارند، در حالی که در چندبرهای با ابعاد بالاتر، سه یا تعداد بیشتری از وجهها در هر ضلع با یکدیگر تماس دارند.۲
زوایا
[ویرایش]زاویه صاف (به انگلیسی: plane angle) زاويه گوشه يك وجه چندضلعی است.
زاویه فضایی (به انگلیسی: solid angle) زاويه اى در فضاى سه بعدی است كه چندوجهى روى رأس مى پوشاند.اين زاويه با سه يا بيشتر از ٣ زاويه زاویه صاف محصور شده.
زاویه دووجهی (به انگلیسی: dihedral angle) زاويه بين دو وجه مجاور است
۱.وجه های جانبی دارای مساحت رویه است
۲.منظور از تماس به خاطر مشترک بودن راس آنها است.
مفاهیم
[ویرایش]چندوجهی محدب
[ویرایش]چندوجهی محدب چندوجهی ای است که جسمی محدب را مشخص میکند. این شرایط را میتوان به روشهای مختلف معادل بیان کرد:
- برای هر جفت از نقاط جسم، خطی که آنها را به هم وصل میکند کاملاً در جسم موجود است (این تعریف معمول مجموعه محدب در فضا است).
- برای هر جفت رأس، خطی که آنها را به وصل میکند کاملاً در جسم موجود است.
- صفحه حاوی هر وجه، فضا را به دو نیمه تقسیم میکند و چند وجهی کاملاً در یکی از این دو نیمه قرار دارد.
چند وجهی غیر محدب را گاهی مقعر مینامند.
اسکلت چندوجهی
[ویرایش]رئوس و ضلعهای چندوجهی گرافی را تشکیل میدهند که اسکلت چند وجهی نامیده میشود. به عنوان مثال، اسکلت چهار وجهی یک گراف کامل با ۴ راس است.
اسکلت چند وجهی محدب یک گراف مسطح است و به همین دلیل قضیه چندوجهی اویلر (که در ادامه توضیح داده خواهد شد) در آن صدق میکند: در واقع میتوان گراف را از یک نقطه داخلی چندوجهی بر روی هر کره ای که در آن نقطه قرار دارد نمایش داد و سپس با استفاده از تصویر کردن استریوگرافیک به روی صفحه نمایش داد. گراف یک چندوجهی پیچیدهتر ممکن است مسطح نباشد.
تور
[ویرایش]تورِ یک چند وجهی، شکل مسطحی است که از تعدادی چندضلعی در امتداد برخی طرفها تشکیل شدهاست، که میتواند در فضا خم شود تا بسته شود و یک چند وجهی تشکیل دهد. تور ابزاری کاربردی برای ساخت چندوجهی کاغذی است.تور شکل گسترده چندوجهی است.
در سال ۱۹۷۵، جی.سی. شپارد پرسید که آیا هر چندوجهی محدب حداقل دارای یک تور ساده است؟ این سؤال که به عنوان حدس دورر یا مسئله تور دورر یا حدس شپارد نیز شناخته میشود، بی پاسخ ماندهاست.
ویژگی ها و مشخصه ها
[ویرایش]تعداد وجوه چندوجهی
[ویرایش]چندوجهیها بر اساس تعداد وجوهشان و بر اساس یونانی کلاسیک دستهبندی و نامگذاری میشوند؛ مثلاً tetrahedron (چهاروجهی) به معنی چندوجهی با چهار وجه، pentahedron (پنجوجهی) به معنی چندوجهی با پنج وجه، hexahedron (ششوجهی) به معنی چندوجهی با شش وجه است و الی آخر به همین شکل نامگذاری میگردند.
زاویه داخلی چندوجهی
[ویرایش]چندوجهی ها از چندضلعی های منتظم درست شده اند. چندوجهی ها مثل چندضلعی ها زاویه داخلی و خارجی دارند.
زاویه داخلی چندوجهی ها بر اساس تعداد وجوه و اضلاع راس بدست می آید.
مثلا چهاروجهی چهار تا مثلث متساوی الاضلاع دارد و اندازه زاویه داخلی وجه آن 60 درجه است و مجموع زاویه داخلی آن برابر با180درجه است.ولی چهاروجهی مجموع زاویه داخلی فضایی اش برابر با720 درجه است.
پس مجموع زاویه داخلی و اندازه زاویه داخلی به ترتیب بر این اساس نوشته می گردد.
شکل و گوشه ها
[ویرایش]برای هر رأس میتوان یک شکل گوشه تعریف کرد که شکل چندوجهی را در اطراف رأس مشخص میکند. تعاریف دقیق متغیرند، اما میتوان شکل گوشه را شکلی تعریف کرد که در اثر بریدن راس چندوجهی پدید میآید. اگر چندضلعی حاصل از این فرایند منتظم باشد، رأس منتظم شمرده میشود.
نماد رأس
[ویرایش]نماد رأس یا پیکربندی رأس علامتی اختصاری برای نشان دادن شکل گوشه یک چندوجهی یا کاشی کاری به عنوان دنباله ای از وجهها در اطراف یک راس است. برای چندوجهیهای یکنواخت فقط یک نوع شکل گوشه وجود دارد و بنابراین پیکربندی راس کاملاً چند وجهی را تعریف میکند.
نماد راس به عنوان دنباله ای از اعداد ارائه شدهاست که تعداد اضلاع وجههای اطراف راس را نشان میدهد. علامت گذاری «a.b.c» یک راس را توصیف میکند که دارای ۳ وجه در اطراف آن است که a و b و c ضلع دارند.
پیکربندی وجه
[ویرایش]دوگانهای یکنواخت که وجه متقارنند، میتوانند با علامات اختصاری مشابهی با پیکربندی رأس که پیکربندی وجه نامیده میشود نشان داده شوند. این نمادها با یک V برای اختلاف نشان داده میشوند. این نماد به شکل شمارش متوالی تعداد وجوهی که در رئوس اطراف وجه قرار دارند مشخص میشوند. مثلاً پیکربندی وجه دوازده لوز وجهی V۳٫۴٫۳٫۴ یا ۲(۳٫۴)V است.
حجم
[ویرایش]جامدات چندوجهی دارای یک مقدار مشخص به نام حجم هستند که میزان فضای اشغال شده را اندازهگیری میکند. خانوادههای ساده چندوجهیها ممکن است فرمولهای ساده ای برای حجم خود داشته باشند. به عنوان مثال، حجم اهرام، منشورها و موازی السطوحها را میتوان به راحتی بر اساس طول ضلع یا مشخصات دیگر بیان کرد.
حجم چندوجهیهای پیچیدهتر ممکن است فرمولهای ساده ای نداشته باشند. با تقسیم چندوجهی به قطعات کوچکتر، حجم این چند وجهیها محاسبه میشود. به عنوان مثال، میتوان حجم یک چند وجهی منتظم را با تقسیم آن به هرمهای برابر محاسبه کرد، به این شکل که که هر هرم دارای یک وجه از چندوجهی به عنوان قاعده و مرکز چندوجهی به عنوان راس آن است.
بهطور کلی، میتوان از قضیه دیورژانس استخراج کرد که حجم یک جامد چندوجهی توسط آن داده میشود:
که در آن مجموع روی وجوه F چندوجهی است، نقطه ای دلخواه روی وجه F بوده، بردار واحد عمود بر F به سمت بیرون چندوجهی و نقطه ضرب ضرب داخلی است.
مساحت
[ویرایش]مساحت چندوجهی های منتظم دارای یک مساحت رویه دارند.وجههای چندوجهی منتظم٬چندضلعی منتظم است.چندوجهی های ثابت مثل منشور٬هرم٬متوازیالسطوح مساحت های ثابتی دارند.هرم ها و منشورهای چندوپهلو نیز بر اساس مساحت منشور بدست میآید اما چون قاعده منشور٬چندضلعی منتظم میباشد٬براساس مجموع مساحت چندضلعی و مساحت جانبی منشور(محیط چندضلعی×ارتفاع)بدست میآید.
مساحت چندوجهی:.
nدر اینجا تعداد وجه و'nتعداد ضلع چندضلعی است عددπدر اینجا برحسب رادیان است
نماد اشلفلی
[ویرایش]نماد اشلفلی نوعی نشانه گذاری برای پلیتوپهای منتظم، از جمله چندوجهیهای منتظم است.
چندوجهیهای منتظم به شکل {p,q} نشانه گذاری میشوند که در آن q نماد اشلفلی شکل گوشهها بوده و p هم نماد اشلفلی چندضلعی هر وجه است.
نماد اشلفلی چندضلعی منتظم محدب به شکل {p} است که در آن p تعداد اضلاع است. نماد اشلفلی چندضلعی منتظم مقعر (ستاره ای) به شکل {p/q} است که در آن p تعداد رئوس و q تعداد اضلاع میان دو رأس در وصل کردن رئوس چندضلعی محدب منتظم برای ساختن آن است.
چندوجهیهایی که نماد اشلفلی آنها قرینه باشند، دوگان یکدیگرند.
تقارن
[ویرایش]بسیاری از چندوجهیهای مورد مطالعه بسیار متقارن هستند، یعنی با انعکاس یا چرخش فضا، شکل ظاهری آنها تغییر نمیکند. هر یک از این تقارنها ممکن است محل یک راس، وجه یا ضلع معین را تغییر دهد، اما مجموعه تمام رئوس (به همین ترتیب وجوه، اضلاع) بدون تغییر است. مجموعه تقارنهای چندوجهی را گروه تقارن آن مینامند.
گفته میشود که تمام اجزایی که توسط تقارنها بر روی یکدیگر قرار میگیرند، یک مدار تقارن را تشکیل میدهند. به عنوان مثال، تمام وجههای مکعب در یک مدار قرار دارند، در حالی که تمام ضلعها در مدار دیگر قرار دارند. اگر تمام اجزا یک بعد معین، مثلاً تمام وجهها، در یک مدار قرار بگیرند، گفته میشود که شکل در آن مدار متقارن است. به عنوان مثال، یک مکعب وجه -متقارن است، در حالی که یک مکعب بریده شده دارای دو مدار تقارن وجه است.
گروههای تقارنی
[ویرایش]بسیاری از تقارنها یا گروههای نقطهای در سه بعد با نام تقارن مرتبط با چند وجهی نامگذاری شدهاند. این گروههای تقارنی شامل:
- T – تقارن چهاروجهی دستسان:گروه چرخشی برای چهاروجهی منتظم
- Td – تقارن چهاروجهی کامل:گروه تقارنی چهاروجهی منتظم
- Th – تقارن پیریتووجهی:تقارن یک پیریتووجهی (دوازده وجهی با وجوه پنج ضلعی غیر منتظم)
- O – تقارن هشت وجهی دستسان:گروه چرخشی مکعب و هشت وجهی
- Oh – تقارن هشت وجهی کامل:گروه تقارنی مکعب و هشت وجهی
- I – تقارن بیست وجهی دستسان:گروه چرخشی بیست وجهی و دوازده وجهی
- Ih – تقارن بیست وجهی کامل:گروه تقارنی بیست وجهی و دوازده وجهی
- Cnv – تقارن هرم n-پهلو
- Dnh – تقارن منشور n-پهلو
- Dnv – تقارن پادمنشور n-پهلو
تقارنهای دستسان تقارن انعکاسی ندارند از این رو دارای دو شکل متقارن هستند که بازتابی از یکدیگر هستند.
خانوادههای مشهور چندوجهیها
[ویرایش]منشوروار
[ویرایش]چندوجهیای است که همه رئوس آن روی دو صفحه موازی قرار گیرند. وجوه جانبی آن میتوانند ذوزنقه یا مثلث باشد. خانوادههای منشوروارها عبارتند از:[۱۱]
| هرم | گوه | متوازیالسطوح | منشور | پاد منشور | گنبد | هرم ناقص | ||
|---|---|---|---|---|---|---|---|---|

|

|

|

|

|

|

| ||
حجم منشوروار از رابطه حاصل میشود که در آن V حجم، A1 و A3 مساحت دو وجه موازی، A2 مقطعی از تقاطع منشوروار با وسط صفحه بین دو وجه موازی و h ارتفاع است.[۱۲]
در زیر انواع منشوروارها شرح داده شده.
- هرم:

«هرم» از گونههای شناختهشدهٔ چندوجهی است. هرم بهطور کلی از یک قاعدهٔ چندضلعی B واقع در صفحهٔ P تشکیل میشود که رئوس آن بهوسیلهٔ وجههای مثلثیشکل به نقطهٔ v که روی صفحهٔ P نیست متصل شدهاند. با این حساب یال M هر هرم، سطحی چندوجهی با وجوه مثلثی خواهد بود. برای ساختن یک هرم میتوان از اکستروژن مرکزی بهره برد. در اکستروژن مرکزی رئوس چندضلعی B در صفحهٔ p در راستای خطوطی همگرا به سوی یک نقطه (v) کشیده میشوند و شکل نهایی هرم به شکل چندضلعی B و جای نقطهٔ v وابسته است.
- روابط: در هرمی به مساحت قاعده S و ارتفاع h و حجم V همواره رابطه برقرار است.
- گوه:

گُوِه نوعی چندوجهی است که وجوه آن شامل دو مثلث و سه ذوزنقه است. گوه دارای ۵ وجه، ۹ ضلع و ۶ رأس است.
- روابط: در گوه مقابل با حجم V همواره رابطه برقرار است.[۱۳]
- متوازیالسطوح:

از انواع منشور است که از شش وجه متوازیالاضلاع ساخته شده. دارای ۱۲ رأس و ۸ ضلع است. حجم متوازی السطوح مقابل با حجم V به وسیله بردارهای و و شکل زیر محاسبه میگردد:
- روابط: از آنجا که متوازی السطوح منشوری ناقائم با قاعده متوازی الاضلاع است، بنابرین حجم برابر با حاصل ضرب مساحت قاعده S در ارتفاع h است.
میدانیم: و: که در اثر یکی شدن:[۱۴]
- منشور

منشور چندوجهیای است که وجههای بالا و پایینش چندضلعیهای همنهشت (مساوی) باشند که در صفحههایی موازی هم قرار دارند. رئوس وجههای بالا و پایین یک منشور با پارهخطهایی به هم وصل میشوند. بااینحساب هر یک از وجههای جانبی منشور یک متوازیالاضلاع است و یال ایجادشده یک سطح چندوجهی است. اگر وجههای بالای منشور با خطهای عمود بر صفحهٔ شامل وجه پایینی آن به وجه پایینی وصل شده باشد، حاصل حالت خاصی از منشور موسوم به «منشور راست» است که در آن همهٔ وجههای جانبی مستطیل هستند. اگر وجوه بالا و پایین یک منشور هم مستطیل باشند منشور راست خاصی به نام مکعب مستطیل تشکیل میشود.
برای ساختن یک منشور میتوان از اکستروژن موازی بهره برد. در اکستروژن موازی رئوس چندضلعی B در صفحهٔ p در راستای خطوطی موازی کشیده میشوند.منشور یکی از خانوادهای منشوروار است.
- روابط: در منشور راستی به مساحت قاعده S و ارتفاع h و حجم V و مساحت کل A همواره روابط زیر برقرارند:
همچنین در منشوری راست با قاعده n-ضلعی منتظم با طول ضلع s و ارتفاع h نیز همواره روابط زیر برقرارند:[۱۵]
- پادمنشور:

پادمنشور نوعی چندوجهی است که دارای دو قاعده همنهشت و موازی، اما پیچ خورده بوده که توسط تعدادی مثلث به هم وصل شدهاند.
- روابط: در پاد منشوری با وجوه چندضلعی منتظم و قاعده n-ضلعی و طول ضلع a و حجم V و مساحت کل A همواره روابط زیر برقرارند:
- گنبد:

گنبد نوعی چندوجهی است که از اتصال دو چندضلعی که یکی از آنها دو برابر دیگری ضلع دارد که وسیله زنجیره ای از مثلثها و مستطیلها حاصل میشود. یک گنبد را میتوان منشوری دید که در آن تعداد اضلاع یکی از قاعدهها با ادغام رأسهای مجاور نصف شدهاست.
- هرم ناقص:

یک هرم ناقص یا بریده هرمی بهطور معمول بخشی از یک مخروط یا هرم است که بین یک یا دو صفحه موازی برش داده میشود و از انواع منشوروار است. هرم ناقص قائم، برش موازی هرم قائم یا مخروط قائم است. یک هرم ناقص n-پهلو متشکل از n وجه ذوزنقه و ۲تا وجه n-ضلعی است.[۱۶]پایهٔ ابلیسک نمونهٔ یک بریدهٔ هرمی است.
- روابط: در هرم ناقصی با مساحت قاعده هرم اولیه B1 و ارتفاع هرم اولیه h1 و مساحت قاعده هرم بریده شده B2 و ارتفاع هرم بریده شده h2 و حجم V همواره رابطه برقرار است. همچنین در مخروط ناقص راستی با شعاع دو قاعده r1 و r2 و سهم h مساحت کل از رابطه زیر به دست میآید:
مساحت کل A هرم ناقصی که قواعدش n-ضلعیهای منتظم اند از رابطه زیر به دست میآید:
- کره

کره ازنوع احجامهندسی است.کره مجموعهنقاطی از فضا است که فاصله مرکز کره تا نقاطکره را شعاع آنگویند.شکلفیزیکی یا اسکلتی کره بهصورت دایرهای است کهدرون آن یکبیضی قرار دارد.کره از نوع چندوجهیها است ولیاز نوع منتظم یاد نشدهاست،چون وجه های کره از چندضلعی منتظم نیست و دارایانحنا است.کره میتواند چندوجهی هارا محاط کند وبر اساس همین محاطکردن میتوانیم حجم چندوجهی هارا محاسبه کرد.اگرچندوجهی در کره محاط شود قطر چندوجهی منتظم با قطر کره برابر میشود.
حجمکره و مساحتکره به اینصورت است:
رابطه مساحتکره و حجمکره به اینصورت است که با مشتق حجمکره،مساحتکره بدستمیآید ولی با انتگرالگیری مساحتکره،حجم کره بدستمیآید.
چندوجهی منتظم
[ویرایش]چندوجهی که همه وجوه آن چندضلعیهای منتظم همنهشت بوده و بهطور یکسان دور هر وجه قرار گرفتهاند. در کل ۹ چندوجهی منتظم وجود دارد که شامل ۵ چندوجهی منتظم محدب (اجسام افلاطونی) و ۴ چندوجهی مقعر منتظم (چندوجهیهای کپلر پوآنسو) هستند.[۱۷]
اجسام افلاطونی
[ویرایش]چندوجهیهای منتظم محدب را اجسام افلاطونی گویند.
تنها پنج جسم افلاطونی وجود دارد که مشخصاتشان در جدول آورده شده.
اجسام افلاطونی ویژگیهای زیر را دارا میباشند:
- همهٔ وجههای آن چندضلعیهای منتظم همنهشت باشند.
- که هیچکدام از وجههای آن با هم تلاقی نکنند، مگر در اضلاع آن.
- تعداد یکسانی از وجهها در هر یک از رأسها به هم برسند.
چندوجهی کپلر-پوآنسو
[ویرایش]هر چندوجهی منتظم مقعر را چندوجهی کپلر-پوآنسو گویند.
چهار چندوجهی کپلر-پوآنسو وجود دارد که مشخصاتشان در جدول آورده شده.[۱۸]
اجسام ارشمیدسی
[ویرایش]گروهی از چندوجهیهای محدبی هستند که وجوه آنها چندضلعیهای منتظم باشند، هرچند لزوماً از یک نوع نباشند، در رأس بهطور یکسان به هم برسند و جزء اجسام افلاطونی و منشورها و پادمنشورها نباشند. در کل ۱۳ جسم ارشمیدسی وجود دارد که مشخصاتشان در جدول آورده شده.
اجسام کاتالان
[ویرایش]اجسام کاتالان یا دوگانهای ارشمیدسی اجسامی هستند که از دوگان کردن (وصل کردن وسط وجوه مجاور) اجسام ارشمیدسی به دست میآیند. به ازای هر جسم ارشمیدسی یک جسم کاتالان وجود دارد که مشخصاتشان در جدول آورده شده.
چندوجهی یکنواخت
[ویرایش]
چندوجهی یکنواخت (Uniform Polyhedron) دارای چندضلعیهای منتظم به عنوان وجه است و رأس-متقارن است. از این رو میتوان گفت که همه رئوس آن با هم همنهشتند.
چندوجهی یکنواخت ممکن است منتظم باشد (اگر هم وجه و هم ضلع متقارن باشد)، شبه منتظم باشد (اگر ضلع-متقارن باشد اما وجه-متقارن نباشد) یا نیمه منتظم باشد (اگر نه ضلع-متقارن باشد و نه وجه-متقارن). نیازی به محدب بودن نیست، بنابراین بسیاری از چندوجهیهای یکنواخت ستاره ای هستند.
دو خانواده شامل بینهایت چندوجهی یکنواخت وجود دارد، همراه با ۷۵ چند وجهی دیگر:
- دارای بینهایت چندوجهی:
- منشورها،
- پادمنشورها.
- استثناهای محدب:
- ۵ جسم افلاطونی:چندوجهیهای منتظم محدب،
- ۱۳ جسم ارشمیدسی:۲ شبه منتظم و ۱۱ نیمه منتظم.
- استثناهای ستاره ای (مقعر):
- ۴ چندوجهی کپلر-پوآنسو:چندوجهیهای منتظم مقعر،
- ۵۳ چندوجهی ستاره ای یکنواخت دیگر:۵ شبه منتظم و ۴۸ نیمه منتظم.
پس تعداد چندوجهیهای یکنواخت که فقط منشور و پادمنشور نیستند برابر ۷۵=۵+۱۳+۴+۵۳ است.
اجسام جانسون
[ویرایش]
اجسامی محدبی که وجوه آنها چندوجهیهای منتظم بوده، اما شامل اجسام افلاطونی و اجسام ارشمیدسی و اجسام منشوری و اجسام پادمنشوری نمیباشند. اگرچه محدودیتی آشکار وجود ندارد که هر چند ضلعی منظم نمیتواند وجه یک جسم جانسون باشد، اما وجههای اجسام جانسونی که وجههایشان یکسان نیست، همیشه ۳، ۴، ۵، ۶، ۸ یا ۱۰ ضلعی هستند. در کل ۹۲ جسم جانسون وجود دارد.
چندوجهی گلدبرگ
[ویرایش]
چندوجهیهای محدبی هستند که از وجوه شش ضلعی و پنج ضلعی ساخته شده و توسط مایکل گلدبرگ در سال ۱۹۳۷ توصیف شدند. همه چندوجهیهای گلدبرگ سه ویژگی زیر را دارا میباشند:
- هر وجه یا پنج ضلعی است یا شش ضلعی.
- دقیقاً سه وجه در هر راس به هم میرسند.
- دارای تقارن بیست وجهی چرخشی هستند.
این نوع چندوجهیها همیشه ۱۲ وجه پنج ضلعی دارند.
چندوجهی ژئودزیک
[ویرایش]
چندوجهی ژئودزیک نوعی چندوجهی محدب است که وجوه آن مثلثند. از آنجا که این نوع چندوجهیها دوگان چندوجهیهای گلدبرگ هستند، بنابرین در هر راس ۶ وجه مثلثی به هم میرسند، به جز ۱۲ رأس که در آنها ۵ وجه به هم میرسند.
دلتاوجهی
[ویرایش]دلتاوجهی نوعی چندوجهی است که همه وجوهش مثلث متساوی الاضلاع باشند. نام آن از حرف یونانی دلتا (Δ) که شبیه مثلث است گرفته شده. بی شمار دلتاوجهی وجود دارد اما از میان آنها فقط ۸ تا محدب هستند که دارای ۴، ۶، ۸، ۱۰، ۱۲، ۱۴، ۱۶ و ۲۰ وجه هستند و شامل ۳ جسم افلاطونی و ۵ جسم جانسون میباشند. اما هیچ دلتاوجهی محدبی با ۱۸ وجه وجود ندارد. مشخصات دلتاوجهیهای محدب در جدول زیر آورده شده:
دوهرمها
[ویرایش]
یک دوهرم n-ضلعی یک چندوجهی است که از پیوستن دو عدد هرم n-ضلعی به دست میآید. یک دوهرم n-ضلعی دارای ۲n وجه مثلثی، ۳n یال و ۲ + n راس است.
فقط سه نوع دوهرم میتوانند یالهای برابر داشته باشند (که این بدان معناست که همه وجوه مثلث متساوی الاضلاع هستند و بنابراین آن دوهرمها دلتاوجهی هستند): دوهرمهای مثلثی، مربعی و پنج ضلعی. بی دوهرم مربعی با ضلعهای یکسان یا هشت وجهی منتظم، در میان اجسام افلاطونی شمرده میشود. دوهرمهای مثلثی و پنج ضلعی با ضلعهای یکسان در میان اجسام جانسون (J12 و J13) قرار میگیرند.
پاددوهرمها
[ویرایش]
یک پاددوهرم n-ضلعی دوگان یک پادمنشور با قاعده n-ضلعی بوده و دارای ۲n وجه همنهشت و متقارن کایت پیچ خورده و ۴n یال و ۲ + ۲n رأس هست. با تقارنی بالاتر وجوه آنها تبدیل به کایت میشود. میتوان پاددوهرمی n-ضلعی را به دو عدد هرم و یک پادمنشور با قاعده n-ضلعی تقسیم کرد.
برای ۲=n شکل حاصل به لحاظ هندسی برابر با چهاروجهی بوده و در صورتی که ۳=n باشد وجوه کایت چندوجهی حاصل لوزی است و در نتیجه پاددوهرم مثلثی نوعی لوزوجه است.
چندوجهی انعطافپذیر
[ویرایش]
چندوجهی انعطافپذیر چندوجهیای بدون هیچ ضلع مرزی است که میتواند شکل خود را بهطور مداوم تغییر داده در حالی که اشکال تمام وجههای آن بدون تغییر است. در بعد ۳ چنین چندوجهیای نمیتواند محدب باشد (این امر در ابعاد بالاتر نیز برای سایر پلیتوپها صادق است). «حدس قوی بیلوز» یا (آن طور که پس از اثباتش در سال ۲۰۱۸ نامیده میشود) «قضیه قوی بیلوز» بیان میکند ناوردای دن هر چندوجهی انعطافپذیر در حال انعطاف ناورداست.
دوگانگی
[ویرایش]برای هر چندوجهی محدب یک دوگانه چندوجهی وجود دارد. به هر گوشه چند وجهی یک وجه از چندوجهی دوگانه دو وجهی اختصاص داده میشود و بالعکس. علاوه بر این، به هر یال یک یال از چند وجهی دوگانه دوطرفه اختصاص داده شده است. دوتایی یک چندوجهی محدب را می توان با حرکت قطبی به سمت جلو به دست آورد. چند وجهی دوتایی به صورت جفت وجود دارد و دوتایی یک دوباره چند وجهی اصلی است. برخی از چندوجهی خود دوگانه هستند، به این معنی که دوگانه چندوجهی با چندوجهی اصلی همخوانی دارد. این چند وجهیها برای مثال چهارضلع، هرم مربع و همه هرمهای منظم هستند.دوگانه یک جامد افلاطونی خود یک جامد افلاطونی است. هگزا وجهی به هشت وجهی دوتایی است و بالعکس، دوازده وجهی دوتایی به ایکو وجهی و بالعکس، و چهارضلعی دوتایی به خود است. هر یک از 13 جامد ارشمیدسی دوتایی به یکی از 13 جامد کاتالانی است و بالعکس. چند وجهی انتزاعی نیز دارای دوگانه است، که علاوه بر این اطمینان می دهد که آنها همان ویژگی اویلر و جهت گیری را به عنوان چند وجهی اصلی دارند. با این حال، این شکل از دوگانگی شکل یک چندوجهی دوگانه را توصیف نمی کند، فقط ساختار ترکیبی آن را توصیف می کند. برای برخی از تعاریف چندوجهی هندسی غیر محدب، چندوجهی وجود دارد که دو وجهی انتزاعی آنها را نمی توان تحت همین تعریف به عنوان چندوجهی هندسی درک کرد.
منابع
[ویرایش]ویکیپدیای فارسی (مقالههای مربوط به «مساحت و حجم» و «چندضلعی منتظم»)
- ↑ مقدمه
- ↑ بخش بدنه صفحه
- ↑ ویکی پدیای انگلیسی:https://en.m.wikipedia.org/wiki/Algebra
- ↑ ۴٫۰ ۴٫۱ ۴٫۲ ۴٫۳ ویکی پدیای فارسی:وhttps://fa.m.wikipedia.org/wiki/%D8%AC%D8%A8%D8%B1 خطای یادکرد: برچسب
<ref>نامعتبر؛ نام «:0» چندین بار با محتوای متفاوت تعریف شده است - ↑ ۵٫۰ ۵٫۱ ۵٫۲ ۵٫۳ «گشتی در دنیای هندسه - ویکیکتاب». بازبینیشده در ۲۰۲۲-۱۱-۱۰.
- ↑ ویکی پدیای آلمانی
- ↑ نگارخانه
- ↑ کتابی برای اقلیدوس است.
- ↑ ویکی کتاب فارسی(ریاضیات پیشرفته/چندوجهی)
- ↑ ویکی پدیای آلمانی
- ↑ William F. Kern, James R Bland, Solid Mensuration with proofs, 1938, p.75
- ↑ B. E. Meserve, R. E. Pingry: Some Notes on the Prismoidal Formula. The Mathematics Teacher, Vol. 45, No. 4 (April 1952), pp. 257-263
- ↑ Harris, J. W. , & Stocker, H. "Wedge". §4.5.2 in Handbook of Mathematics and Computational Science. New York: Springer, p. 102, 1998.
- ↑ Coxeter, H. S. M. Regular Polytopes, 3rd ed. New York: Dover, p. 122, 1973.
- ↑ William F. Kern, James R. Bland, Solid Mensuration with proofs, 1938, p.81
- ↑ William F. Kern, James R. Bland, Solid Mensuration with proofs, 1938, p. 67
- ↑ «Regular Polyhedron». MathWorld. بازبینیشده در ۱۰ آوریل ۲۰۱۴.
- ↑ Coxeter, Star polytopes and the Schläfli function f(α,β,γ) p. 121 1. The Kepler–Poinsot polyhedra
هشت وجهی منتظم
هشت وجهی منتظم یک جسم سه بعدی بسته است که از هشت مثلث متساوی الاضلاع تشکیل شده است.این جسم از نوع چندوجهی ها به حساب می آید و جزء اجسام افلاطونى است.این نوع حجم از احجام هندسی است و دارای دو هرم به قاعده مشترک مربع دارد.این حسم دارای 12یال،6راس،8وجه و یک قاعده و دو راس مرکز دارد.این نوع حجم نیز از احجام هرمی است.می توان این نتیجه را گرفت،هشت وجهی یک افلاطونی-چندوجهی-هرمی است.

روابط هندسی
[ویرایش]دوگان
[ویرایش]یک هشت و جهی منتظم که در مکعب محاط می شود. روابط های زیر برقرار است.
- ضلع هشت وجهی محاطی نصف وتر صفحه مکعب است.
- ارتفاع هشت وجهی برابر با ارتفاع مکعب است
- راس مرکز هشت وجهی در مرکز مربع ها قرار دارد.
- وجه مکعب با قاعده هشت وجهی ها باهم تشابه دارند.
هشت وجهی ستاره ای
[ویرایش]
این نوع جسم از نوع چندوجهی های ستاره ای است و اضلاع چهاروجهی ها برابر با اضلاع هشت وجهی است.رئوس هشت ضلعی در نقاط میانی لبه های چهار وجهی قرار دارد و از این نظر به چهار وجهی ارتباط دارد به همان صورتی که مکعب و ایکوزید وجه با سایر جامدات افلاطونی ارتباط دارند.
چندوجهی اسناب
[ویرایش]همچنین می توان لبه های یک هشت وجهی را به نسبت میانگین طلایی تقسیم کرد تا رئوس یک ایکو وجهی مشخص شود . این کار با قرار دادن بردارها در امتداد لبه های هشت وجهی به گونه ای انجام می شود که هر وجه توسط یک چرخه محدود شود، سپس به طور مشابه هر یال را به میانگین طلایی در امتداد جهت بردار آن تقسیم می کنیم. پنج هشت ضلعی وجود دارد که هر ایکوساهدر معین را به این شکل تعریف می کنند و با هم یک ترکیب منظم را تعریف می کنند . به ایکوساهدری که به این روش تولید می شود، هشت وجهی اسناب یا اسنوب نامیده می شود
معادله هشت وجهی منتظم
[ویرایش]مختصات دکارتی
[ویرایش]یک هشت ضلعی با طول یال 2√ را می توان با مرکز آن در مبدا و رئوس آن بر روی محورهای مختصات قرار داد. مختصات دکارتی رئوس پس از آن است
- ( ± 1، 0، 0 )؛
- ( 0, ± 1, 0 );
- ( 0، 0، 1±).
در سیستم مختصات دکارتی x – y – z ، هشت وجهی با مختصات مرکزی ( a ، b ، c ) و شعاع r مجموعه ای از تمام نقاط ( x ، y ، z ) است به طوری که برابر با این رابطه است.
در این معادله ما از قدر مطلق برای مثبت شدن عبارات منفی استفاده می کنیم.
حجم و مساحت
[ویرایش]حجم
[ویرایش]حجم یک هش وجهی اینگونه بدست می آید که ابتدا ارتفاع را بدست آوریم،بعد مساحت قاعده آن بدست آوریم هشت وجهی دارای دوهرم است و هرم ها دارای ارتفاع هستندو ارتفاع هشت وجهی مجموع دو ارتفاع این دو هرم است.قاعده دوهرم نیز باهم هم مساحت و مشترک است.
ارتفاع
[ویرایش]برای بدست ارتفاع،ابتدا باید مثلث متساوی الاضلاع را به دو مثلث قائم الزاویه نصف کرد و قاعده را نیز نصف کرد. سپس طبق رابطه فیثاغورس می نویسیم.
این ربطه،رابطه مجذور ارتفاع مثلث است که این گونه ارتفاع اصلی نوشته می شود.
و بعد ارتفاع را چون مثلث است نصف می کنیم و برابر با این رابطه است.
ارتفاع مثلث متساوی الاضلاع نوعی وتر شده است و ضلع مجاور بعدی ضلع مربع است که نصف شده است.چون مربع اضلاع های عمود درون آن با اضلاع مربع و مثلث متساوی الاضلاع در هشت وجهی برابر است.پس ارتفاع اصلی به روش فیثاغورس زیر بیان می شود.
با جذر گرفتن ارتفاع اصلی با دوبرابر کردن و مجموع ارتفاع آن بدست می آید.
مساحت قاعده
[ویرایش]مساحت قاعده مربع است و مساحت مربع برابر با ضلع به توان دو است.
محاسبه حجم
[ویرایش]با ضرب ثلث مساحت قاعده در ارتفاع حجم بدست می آید
مساحت
[ویرایش]مساحت هشت وجهی برابر است با مجموع مساحت هشت تا مثلث متساوی الاضلاع است.
مساحت مثلث متساوی الاضلاع برابر با این رابطه است. پس مساحت هشت وجهی این گونه است.
معادله مساحت و حجم
[ویرایش]اگر یک هشت ضلعی کشیده شده باشد تا معادله را رعایت کند
فرمول های سطح و حجم گسترش می یابد تا تبدیل شود
به علاوه تانسور اینرسی هشت وجهی کشیده شده است
اینها به معادلات هشت وجهی منتظم کاهش می یابند
منابع
[ویرایش]ویکی پدیای انگلیسی
چنبره
چَنبَره (به انگلیسی: torus) در هندسه، نوعی رویه دورانی است که از طریق دوران یک دایره در فضای سهبعدی، حول یک محور که با دایره همصفحه است، ایجاد میشود.

در هندسه
[ویرایش]چنبره را میتوان به صورت پارامتری تعریف کرد:
که در آن:
- پارامتر u و v در بازه [۰, ۲π) قرار دارند.
- R شعاع از مرکز تا محور چنبره است
- r شعاع چنبره است
در دستگاه مختصات دکارتی میتوان تعریف کرد:
که به طور سادهتر میتوان نوشت:
A مساحت رویه چنبره از معادله:
و V حجمی که یک چنبره محصور میکند از
بدست میآید.
در محور چرخش
[ویرایش]اگر محور چرخش با دایره تماس نداشته باشد، سطح به شکل حلقه است و به آن چنبره چرخش می گویند. اگر محور چرخش مماس بر دایره باشد، سطح یک چنبره شاخ است. اگر محور چرخش دو بار از دایره عبور کند، سطح یک چنبره دوکی است. اگر محور چرخش از مرکز دایره عبور کند، سطح یک چنبره منحط، یک کره دوپوشیده است. اگر منحنی چرخان یک دایره نباشد، سطح یک شکل مرتبط، یک حلقوی است. اشیاء دنیای واقعی که به یک چنبره انقلاب نزدیک می شوند عبارتند از حلقه های شنا، لوله های داخلی و حلقه های رینگت. عدسی های عینک که ترکیبی از اصلاح کروی و استوانه ای هستند، لنزهای توریک هستند
چگونگی
[ویرایش]یک چنبره را نباید با یک چنبره جامد که با چرخش یک دیسک به جای یک دایره حول یک محور تشکیل می شود، اشتباه گرفت. چنبره جامد یک چنبره به اضافه حجم داخل چنبره است. اشیاء دنیای واقعی که تقریباً به یک چنبره جامد میرسند عبارتند از حلقههای O-Ring، شناورهای نجات غیر قابل باد کردن، دونات حلقهای و شیرینی.
در توپولوژی
[ویرایش]در توپولوژی، یک چنبره حلقوی با حاصلضرب دکارتی دو دایره همومورف است: S1 × S1، و دومی به عنوان تعریف در آن زمینه در نظر گرفته میشود. این یک 2 منیفولد فشرده از جنس 1 است. چنبره حلقه یکی از راههای جاسازی این فضا در فضای اقلیدسی است، اما راه دیگر برای انجام این کار، حاصلضرب دکارتی تعبیه S1 در صفحه با خودش است. این یک جسم هندسی به نام چنبره کلیفورد، سطحی در 4 فضای ایجاد می کند. در زمینه توپولوژی، چنبره هر فضای توپولوژیکی است که با چنبره همومورف باشد.[1] سطح یک فنجان قهوه و یک دونات هر دو توری توپولوژیکی با جنس یک هستند. نمونه ای از چنبره را می توان با برداشتن یک نوار مستطیلی از مواد انعطاف پذیر، به عنوان مثال، یک ورق لاستیکی، و اتصال لبه بالایی به لبه پایین، و لبه سمت چپ به لبه سمت راست، بدون هیچ گونه پیچ و تاب ساخت (مقایسه کنید نوار موبیوس).
تولید چنبره
[ویرایش]کره و چنبره حجمهاییاند که با چرخاندن دایره حول یک محور ایجاد میشوند. با چرخاندن دایره به دور محوری که با آن در یک صفحه باشد چنبره به دست میآید. بسته به فاصلهٔ محور چرخش از مرکز دایره سه گونهٔ متفاوت چنبره ایجاد میشود. اگر فاصلهٔ محور از مرکز دایره از شعاع دایره کوچکتر باشد و محورْ دایره را در دو نقطه قطع کند حجم حاصل «چنبرهٔ دوکی»، اگر فاصلهٔ محور از مرکز دایره با شعاع دایره مساوی باشد (s=r) و محورْ دایره را در یک نقطه لمس کند حجم حاصل «چنبرهٔ شاخی»، و اگر فاصلهٔ محور از مرکز دایره از شعاع دایره بیشتر باشد و محور با دایره تقاطع نداشته باشد حجم حاصل «چنبرهٔ حلقهای» خواهد بود. چنبرهٔ حلقهای در این میان ویژگی خاصی دارد و آن این است که علاوه بر دو خانوادهٔ دوایر نصفالنهاری و دوایر موازی، دو خانوادهٔ از دوایر دیگر نیز در آن شکل میگیرد (یعنی هر نقطه روی سطح چنبرهٔ حلقهای روی محیط چهار دایره روی سطح آن قرار دارد) که به دوایر ولاسیون موسومند.
اگر محور چرخش بر هر کدام از قطرهای دایره منطبق باشد حاصل کره خواهد بود (کره را میتوان حالت خاص چنبره دانست).

منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیاس انگلیسی
دوران
دوران حرکت دایره ای یک جسم حول محور چرخش در جهت عقربه های ساعت یا خلاف جهت عقربه های ساعت است. یک جسم سه بعدی ممکن است دارای بی نهایت محور چرخش باشد.
اگر محور چرخش به صورت داخلی از مرکز جرم خود بدن عبور کند ، آنگاه گفته میشود که جسم در حال چرخش یا چرخش خودکار است و محل تلاقی سطح محور را میتوان قطب نامید . چرخش حول یک محور کاملاً خارجی، مثلاً سیاره زمین به دور خورشید ، چرخان یا در حال گردش نامیده می شود ، معمولاً زمانی که توسط گرانش ایجاد می شود ، و انتهای محور چرخش را می توان قطب های مداری نامید .
ریاضیات
[ویرایش]از نظر ریاضی ، چرخش یک حرکت بدن سفت و سخت است که بر خلاف ترجمه ، یک نقطه را ثابت نگه می دارد. این تعریف برای چرخش در دو بعد و سه بعد (به ترتیب در یک صفحه و در فضا) اعمال می شود.
تمام حرکات سفت و سخت بدن چرخش، ترجمه یا ترکیبی از این دو هستند.
چرخش به سادگی یک جهت شعاعی پیشرونده به یک نقطه مشترک است. آن نقطه مشترک در محور آن حرکت قرار دارد. محور 90 درجه عمود بر صفحه حرکت است.
اگر چرخش حول یک نقطه یا محور با چرخش دوم حول همان نقطه/محور دنبال شود، چرخش سوم حاصل می شود. معکوس ( معکوس ) یک چرخش نیز یک چرخش است. بنابراین، چرخشهای حول یک نقطه/محور یک گروه را تشکیل میدهند . با این حال، یک چرخش حول یک نقطه یا محور و یک چرخش حول یک نقطه/محور متفاوت ممکن است منجر به چیزی غیر از یک چرخش شود، به عنوان مثال، تبدیل.
چرخش حول محورهای x ، y و z چرخش اصلی نامیده می شود . چرخش حول هر محوری را می توان با چرخش حول محور x و به دنبال آن یک چرخش حول محور y و به دنبال آن چرخش حول محور z انجام داد. یعنی هر چرخش فضایی را می توان به ترکیبی از چرخش های اصلی تجزیه کرد.
در دینامیک پرواز ، چرخشهای اصلی بهعنوان انحراف ، گام و رول (معروف به زوایای تایت-برایان ) شناخته میشوند. این اصطلاح در گرافیک کامپیوتری نیز استفاده می شود .
هندسه
[ویرایش]در هندسه دوران به صورت چرخش حجم سازی انجام می گردد،به این نوع حرکت،حرکت اسپینی یا دوران اسپینی گویند.در دوران حجم آن ضلعی که حول شکل آن دوران می دهد بچرخد ارتفاع میشود اما آن ضلعی که چرخیده می شود شعاع آن جسم است.
اصول های دورانی
از دوران یک مستطیل حول یکی از اضلاعش= استوانه
از دوران یک مثلث قائمالزاویه حول یکی از اضلاع مجاورش= مخروط
از دوران یک ذوزنقه قائم الزاویه حول ضلع قائم= مخروط ناقص
از دوران یک مثلث قائم الزاویه حول وتر= دو مخروط
از دوران یک دایره حول قطر به اندازه○180= کره
از دوران یک نیم دایره حول قطر به اندازه○360= کره
از دوران یک بیضی حول یکی از قطر هایش یک کره گون به وجود می آید.
از دوران یک سهمی حول یکی از قطرهایش یک سهمی گون به وجود می آید
از دوران یک هذلولی حول یکی از قطرهایش ،یک هذلولی گون به وجود می آید.
محور ثابت مقابل نقطه ثابت
[ویرایش]نتیجه نهایی هر دنباله ای از چرخش هر جسم به صورت سه بعدی حول یک نقطه ثابت همیشه معادل چرخش حول یک محور است. با این حال، یک جسم ممکن است به طور فیزیکی به صورت سه بعدی حول یک نقطه ثابت روی بیش از یک محور به طور همزمان بچرخد، در این صورت هیچ محور ثابت چرخشی وجود ندارد - فقط نقطه ثابت. با این حال، این دو توصیف را می توان با هم تطبیق داد - چنین حرکت فیزیکی را همیشه می توان بر حسب یک محور چرخش دوباره توصیف کرد، مشروط بر اینکه جهت آن محور نسبت به جسم اجازه داده شود لحظه به لحظه تغییر کند.
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
زاویه مرکزی
زاویه مرکزی زاویهای است که راس آن مرکز O یک دایره است و پاها (اضلاع) آن دایره را در دو نقطه متمایز A و B قطع میکنند . طول قوس زاویه مرکزی یک دایره به شعاع یک است (بر حسب رادیان اندازه گیری می شود ). زاویه مرکزی به عنوان فاصله زاویه ای قوس نیز شناخته می شود .
اندازه یک زاویه مرکزی Θ 0 ° < Θ < 360 درجه یا 0 < Θ < 2π (رادیان) است. هنگام تعریف یا ترسیم یک زاویه مرکزی، علاوه بر مشخص کردن نقاط A و B ، باید مشخص شود که زاویه مورد نظر زاویه محدب (<180 درجه) یا زاویه بازتاب (> 180 درجه) باشد. به طور معادل، باید مشخص کرد که حرکت از نقطه A به نقطه B در جهت عقربه های ساعت است یا خلاف آن.
فرمول ها
[ویرایش]اگر نقاط تقاطع A و B پایه های زاویه با دایره قطر تشکیل دهند ، آنگاه Θ = 180 درجه یک زاویه مستقیم است . (در رادیان، Θ = π .)
بگذارید L قوس فرعی دایره بین نقاط A و B باشد و R شعاع دایره باشد .
اگر زاویه مرکزی Θ توسط L تحت فشار قرار گیرد ، آنگاه
اثبات (برای مدرک)
محیط دایره ای با شعاع R برابر 2π R است و قوس کوچک L برابر است با (Θ/360 درجه) بخش متناسب کل محیط ( قوس را ببینید ). بنابراین:
اثبات (برای رادیان)
محیط دایره ای با شعاع R برابر 2π R است و قوس کوچک L برابر است با (Θ/2π) بخش متناسب کل محیط ( قوس را ببینید ). بنابراین
اگر زاویه مرکزی Θ توسط قوس کوچک L تحت تأثیر قرار نگیرد ، آنگاه Θ زاویه بازتابی است و اگر یک مماس در A و یک مماس در B در نقطه بیرونی P قطع شوند ، آنگاه با نشان دادن مرکز به صورت O ، زوایای ∠ BOA (محدب) و ∠ BPA مکمل هستند (مجموع 180 درجه).
زاویه مرکزی یک چند ضلعی منتظم
[ویرایش]یک چند ضلعی منتظم با n ضلع دایره ای محصور دارد که تمام رئوس آن روی آن قرار دارند و مرکز دایره نیز مرکز چند ضلعی است. زاویه مرکزی چند ضلعی منتظم در مرکز توسط شعاع دو راس مجاور تشکیل می شود. اندازه گیری این زاویه است2π/n
دربعد بالاتر
[ویرایش]در یک کُره یا بیضیگون، زاویهٔ مرکزی را با توجه به دایرهٔ بزرگ مشخص میکنیم. مختصات معمولی که برای یک نقطه روی یک کره یا بیضیگون در نظر گرفته میشود، همان عرض جغرافیایی مزدوج با نماد ("Lat") یا و طول جغرافیایی مزدوج با نماد ("Long") یا است. و در حقیقت نقطهٔ نسبت به دایرهٔ بزرگ سنجیده میشود.
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
زاویه محاطی
زاویهٔ محاطی در هندسه هنگامی ساخته میشود که دو خط گذرا از روی دایره (یا در تباهیدگی یک خط قطع کننده و یک خط مماس) با یکدیگر روی پیرامون دایره برخورد کنند.
به بیان سادهتر اگر یک زاویه درون یک دایره باشد و ضلعهای زاویه، دو وتر از دایره باشد که با هم یک نقطهٔ مشترک دارند، چنین زاویهای زاویهٔ محاطی نام دارد. در کتاب سوم اصول اقلیدس، گزارههای ۲۰ تا ۲۲، ویژگیهای این زاویه گفته شدهاست. اگر یک زاویهٔ مرکزی و یک زاویهٔ محاطی هر دو یک کمان از دایره را دربرداشته باشند، اندازهٔ زاویهٔ محاطی نصف زاویهٔ مرکزی خواهد بود
اثبات
[ویرایش]زاویهٔ محاطی با یک قطر
[ویرایش]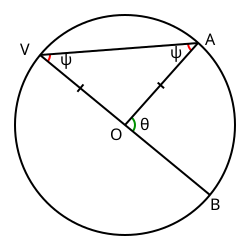
اگر O مرکز دایره باشد، دو نقطهٔ بر روی محیط دایره انتخاب کنید و آنها را به ترتیب V و A بنامید. V را به O وصل کنید و آن را ادامه دهید تا با پیرامون دایره در نقطهٔ B برخورد کند. چون این خط از مرکز دایره گذشتهاست پس قطر دایرهاست در نتیجه V در یک سوی قطر و B در سوی دیگر آن جای گرفتهاست. حال زاویهای بکشید که راس آن در نقطهٔ V باشد و دو لبهٔ آن از A و B بگذرد.
نقطهٔ A را به O وصل کنید. زاویهٔ BOA یک زاویهٔ مرکزی است. آن را θ بنامید. دو پاره خط OA و OV با هم برابرند چون هر دو شعاع دایرهاند. پس مثلث VOA متساویالساقین است. در نتیجه دو زاویهٔ BVA (زاویهٔ محاطی) و VAO با هم برابرند. هر دوی این زاویهها را ψ مینامیم.
زاویههای BOA و AOV با هم مکمل اند و مجموع آنها ۱۸۰ درجه میشود. چون خط VB از O میگذرد و یک خط راست است پس اندازهٔ زاویهٔ AOV از رابطهٔ ۱۸۰° − θ بدست میآید.
از سوی دیگر میدانیم که مجموع زاویههای داخلی مثلث ۱۸۰ درجهاست. سه زاویهٔ داخلی مثلث VOA عبارتند از: پس بنابراین.
۱۸۰° را از دو سوی تساوی کم می کنیم.
که در آن θ زاویهٔ مرکزی کمان AB است و ψ زاویهٔ محاطی همان کمان است که اندازهای برابر با نصف آن دارد.
زاویهٔ محاطی و مرکز دایره درون آن
[ویرایش]
دایرهای با مرکز O را در نظر بگیرید. سه نقطهٔ D،VوC را بر روی آن برگزینید. دو پاره خط VC و VD را بکشید. زاویهٔ DVC یک زاویهٔ محاطی است. حال خط VO را بکشید و آن را ادامه دهید تا با سوی دیگر دایره در نقطهٔ E برخورد کند. کمان روبرو به زاویهٔ محاطی DVC، کمان DC نام دارد.
کمان DC نقطهٔ E را در بر میگیرد و میدانیم که این نقطه بر روی قطری از دایره قرار دارد. از سوی دیگر زاویههای DVE و EVC هر دو زاویهٔ محاطیاند. در بخش پیشین بدست آوردیم که اگر یک ضلع زاویهٔ محاطی از مرکز دایره بگذرد اندازهٔ آن برابر نصف کمان روبروی آن است. حال از دادههای بخش پیشین بهره میگیریم:
پس داریم:
نتیجه میگیریم:
حال خطهای OC و OD را میکشیم. زاویهٔ DOC یک زاویهٔ مرکزی است. همچنین زاویههای DOE و EOC هم زاویههای مرکزیاند؛ و میدانیم:
اگر فرض کنیم:
آنگاه:
پیشتر از بخش یک میدانیم که و با توجه به تمامی این دادهها و معادلهٔ (۲) بدست میآوریم که:
با توجه به رابطهٔ (۱) خواهیم داشت:
زاویهٔ محاطی که مرکز دایره در بیرون آن جای دارد
[ویرایش]
دایرهای با مرکز O را در نظر بگیرید. سه نقطهٔ E,C,V و D را بر روی آن برگزینید. دو پاره خط VC و VD را بکشید. زاویهٔ DVC یک زاویهٔ محاطی است. حال خط VO را بکشید و آن را ادامه دهید تا با سوی دیگر دایره در نقطهٔ E برخورد کند. کمان روبرو به زاویهٔ محاطی DVC، کمان DC نام دارد.
میدانیم که نقطهٔ E که بر روی قطری از دایره جای دارد. همچنین میدانیم که زاویههای DVE و EVC هم زاویههایی محاطیاند. در بخشهای پیشین نشان دادیم که اندازهٔ زاویهٔ محاطی که ضلعش از روی مرکز دایره بگذرد برابر نصف کمان روبرویش است. پس خواهیم داشت:
- .
اگر فرض کنیم:
آنگاه
خطهای OC و OD را بکشید. زاویهٔ DOC یک زاویهٔ مرکزی است همچنین میدانیم که زاویههای DOE و EOC هم زاویههایی مرکزیاند. با توجه به آنکه
اگر فرض کنیم
آنگاه خواهیم داشت:
با توجه به نکتههایی که در بخش یک گفته شد میدانیم که و است. با توجه به این تساویها و رابطهٔ (۴):
پس، از رابطهٔ (۳) خواهیم داشت:
نکاتی درباره زاویه محاطی
[ویرایش]- همه زاویههای محاطی روبروی یک کمان با هم برابرند.
- روبروی یک کمان میتوان بینهایت زاویه محاطی رسم کرد.
- زاویه محاطی روبروی قطر دایره برابر با °۹۰ است.
- اگر همه رأسهای یک چهارضلعی روی محیط دایره قرار داشته باشند، زوایای روبروی هم مکمل یکدیگرند.
- همه زاویه های محاطی نصف کمان روبه رو هستند
- زاویه محاطی با زاویه ظلی در یک راس هستند و برابر هستند
منابع
[ویرایش]ویکی پدیای فارسی
زاویه ظلی
زاویه ظلی، نوعی دیگر از زاویههایی است که در دایره رسم میشود که راس آن روی دایره قراردارد و یکیاز اضلاع آن مماس بر دایره است و دیگری وتری از دایره است. زاویه ظلی اندازه زاویه اش نصف کمان روبه رو است،وبا زاویه محاطی برابر است،چون هردو راس آنها روی دایره قرار دارد.

اثبات زاویه ظلی
[ویرایش]زاویه محاطی را در نظر بگیرید و به همراه زاویه ظلی در نظر بگیرید,ابتدا برای اندازه گرفتن زاویه ظلی ابتدا زاویه محاطی را رسم می کنیم.

زاویهDBEزاویه محاطی است و زاویهDBCزاویه ظلی است.زاویه مرکزی ما زاویهDAEاست. به متن زیر توجه کنید
اثبات زاویه محاطی
[ویرایش]
برای ثابت کردن زاویه محاطی که نصف کمان روبه رو است ابتدا مثلثی می کشیم که متساوی الساقین باشد،در هر مثلث زاویه خارجی اش مجموع زاویه های غیر مجاورش است و چون مثلث فوق متساوی الساقین است و در مثلث متساوی الساقین دو زاویه ساق باهم برابر اند و زاویه غیر مجاور زاویه کمان هستند پس زاویه کمان را نصف کرده و زاویه محاطی که زاویه ساق بودند را بدست می آوریم.
اثبات زاویه ظلی به کمک زاویه محاطی
[ویرایش]
اندازه زاویهDAEبرابر با°90است و زاویهCBEهم°90است و زاویهDBEچون محاطی است و نصف کمان است پس °45 درجه می شود.زاویه محاطی و ظلی جزء زاویهCBE است و زاویه محاطی نیز45درجه بود،پس زاویه ظلی نیز برابر با 45-90برابر با°45درجه است
قضیه:اندازه زاویه ظلی برابر با زاویه محاطی کمان است و نصف کمان روبه رو اشت
مسئله
[ویرایش]اندازه زاویه ظلی این شکل را بدست آورید.

منابع
[ویرایش]هندسه پایه یازدهم(ص12)
ریاضیات پایه هشتم(تحقیق زاویه محاطی)
ویکی پدیای فارسی
زاویه فضایی
زاویه فضایی یا زاویه حجمی٬نوعی زاویه است که در فضای سهبعدی قرار دارد که یکجسم یک نقطه روی یکنقطه ای میپوشاند که از دید بزرگ به نظر میرسد. زاویه از سطح کره ای درست شده.این نوع زاویه بر اساس رویه کره و شعاع آن اندازه گیری میشود. زاویه فضایی را با نشان میدهند.
مقدار
[ویرایش]مقدار امگا بر اساس سطح مساحت کره تقسیم بر مجذور آن بدست می آید با ضرب عدد که در زاویه فضایی یک ضریب متناسب در زاویه فضایی و سطح مساحت کره و شعاع است،بدست می آید
یکای سنجش زاویهٔ فضایی در سیستم استاندارد بینالمللی واحدها استرادیان است. در یکای استرادیان، ضریب تناسب برابر با یک است.
در مختصات کروی، جزء زاویهٔ فضایی برابر با این رابطه است
زاوایای ثابت برای اشیاءمشترک
[ویرایش]مخروط،کلاهک کروی،نیمکره
[ویرایش]زاویه جامد یک مخروط با راس آن در راس زاویه جامد و با زاویه راس2θ، مساحت یک کلاهک کروی روی یک کره واحد است .
در اینجاcosθبه این صورت نوشته می گرددموارد فوق با محاسبه انتگرال دوگانه زیر با استفاده از عنصر سطح واحد در مختصات کروی بدست می آید :
می توان این مبحث را بدون انتگرال و دیفرانسیل استدلال و اثبات کرد.برای اولین بار بیش از 2200 سال پیش ارشمیدس ثابت کرد که مساحت سطح یک کلاهک کروی همیشه برابر با مساحت دایره ای است که شعاع آن برابر است با فاصله از لبه کلاهک کروی تا نقطه ای که محور تقارن کلاهک با کلاهک قطع می شود. در نمودار این شعاع به صورت داده شده است
بنابراین برای یک کره فضایی زاویه فصایی کلاهک کروی به صورت داده شده است
وقتی θ =π/2، کلاهک کروی تبدیل به نیمکره ای با زاویه فضایی 2 برابر باπ می شود.
زاویه جامد مکمل مخروط استاین همچنین زاویه جامد بخشی از کره سماوی است که یک ناظر نجومی واقع در عرض جغرافیایی θ می تواند در حین چرخش زمین ببیند. در خط استوا تمام کره آسمانی قابل مشاهده است. در هر دو قطب، فقط یک نیمه.
زاویه جامد که توسط قطعه ای از کلاهک کروی که توسط صفحه ای در زاویه γ از محور مخروط بریده می شود و از رأس مخروط می گذرد، با فرمول بدست می آید.
به عنوان مثال، اگر γ = - θ , آنگاه فرمول به فرمول کلاهک کروی بالا کاهش می یابد: عبارت اول به π و دومین π cos θ می شود.
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
قطاع
قطاع دایره یا قطاع بخشی از یک قرص یا دایرهاست که به دو شعاع و یک کمان محدود شدهاست. θ زاویهٔ مرکزی روبروی کمان، شعاع دایرهrوLطول کمان است. زاویه ای که با اتصال نقاط انتهایی کمان به هر نقطه از محیط که در بخش نیست، برابر با نیمی از زاویه مرکزی است.
یک قطاع با زاویهٔ ۱۸۰ درجه را نیمدایره و با زاویهٔ ۹۰ درجه را ربع دایره مینامند. اگر دو انتهای کمان را به هر نقطهای غیر از مرکز دایره وصل کنیم، بخش پدید آمده قطاع نخواهد بود؛ و زاویهٔ ساخته شده در آن هم زاویهٔ مرکزی نخواهد بود.
مساحت
[ویرایش]مساحت سراسر دایره برابر است پس مساحت یک قطاع برابر است با حاصل ضرب نسبت زاویهای که دربر دارد به زاویهٔ کل دایره (۳۶۰ درجه) در مساحت کل دایره. اگر زاویهٔ θ به رادیان باشد، مساحت قطاع خواهد بود:
و اگر θ به درجه باشد:
روش دیگر آن است که مساحت این قطاع را از راه انتگرال زیر بدست آوریم:
محیط
[ویرایش]محیط یک قطاع برابر است با مجموع طول کمان آن و دو شعاع دایره:
که در اینجا θ به رادیان است.
طول کمان
[ویرایش]فرمول طول کمان این است:که در آن L نشان دهنده طول قوس، r نشان دهنده شعاع دایره و θ نشان دهنده زاویه رادیان ساخته شده توسط کمان در مرکز دایره است. اگر مقدار زاویه به درجه داده شود، می توانیم از فرمول زیر نیز استفاده کنیم:
طول آکورد
[ویرایش]طول یک وتر تشکیل شده با نقاط انتهایی کمان باکه در آن C نشان دهنده طول وتر، R نشان دهنده شعاع دایره، وθنشان دهنده عرض زاویه ای بخش بر حسب رادیان است.
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
رادیان
رادیان زاویه مرکزی مقابل به کمانی از دایره است که طول آن با شعاع دایره برابر است. یعنی زاویه مرکزیِ متناظر با محیط دایره، مساویِ رادیان و اندازه زاویه نیم صفحه، رادیان و اندازه زاویه قائمه، رادیان است.
اندازهٔ بر حسب رادیان برای عملیات تحلیلی و نظری مناسب ولی برای استفادههای عملی نسبتاً نامناسب است، چون عدد گنگ است. اگر از نقطهای روی دایره شروع کرده پشت سر هم کمانهای واحد یعنی کمانهایی به اندازهٔ ۱ رادیان جدا کنیم، هرگز به نقطهٔ شروع باز نخواهیم گشت. اما نظام اندازهگیری معمولی طوری طراحی شده که پس از ۳۶۰ بار کمان یک درجهای، به نقطهٔ شروع برمیگردیم (یعنی یک دور به ۳۶۰ واحد صحیح تقسیم شده است).

موارد زاویه و رادیان
[ویرایش]در همهٔ موارد عملی، زاویه بر حسب واحدهایی اندازهگیری میشود که از تقسیم زاویهٔ راست (قائم) به اجزاء برابر به دست میآیند. اگر تعداد این اجزا ۹۰ باشد، واحد همان واحد آشنای درجه است. تقسیم زاویهٔ راست به ۱۰۰ جزء برای نظام اعشاری ما مناسبتر است (واحد گرادیان)، ولی آن هم معرف همین شیوهٔ اندازهگیری است. اما در بررسیهای نظری بهتر است برای مشخص کردنِ اندازهٔ زاویه، از شیوهٔ اساساً متفاوتی استفاده کنیم که آن را اندازهٔ رادیانی یا اندازه بر حسب رادیان مینامند.
بسیاری از فرمولهای مهمی که شامل تابعهای مثلثاتیِ زاویهها هستند، در این نظام شکل سادهتری دارند تا در نظام اندازهگیری بر حسب درجه.
بیشتر از رادیان
[ویرایش]حال سؤال اینجاست که آیا میتوان بیشتر از زاویهای داشت؟جواب مثبت است. شما میتوانید تا هر چقدر به گردش روی محیط دایره ادامه دهید و مقدار رادیان را زیاد کنید. نکته اینجاست که به زوایای تکراری میرسید. یعنی هر کدام از زوایای صفر تارا که با ضریبی ازجمع کنید، برابر با همان زاویه است.
علت وجود رادیان
[ویرایش]حتما با مفهوم درجه آشنایی دارید. درجه واحدی برای اندازهگیری زاویه است.یک دایره کامل برابر ۳۶۰ درجه، نیم دایره برابر ۱۸۰ درجه و ربع دایره برابر با ۹۰ درجه است.
اما تا به حال از خود پرسیدهاید چرا یک دایره کامل را ۳۶۰ درجه میگوییم؟ علت چیست؟
واحد درجه از زمانهای خیلی قدیم هم وجود داشته است و در واقع نوعی قرارداد است. اینکه چرا انسانهای قدیمی، یک درجه را برابر با یک دایره گرفتهاند، معلوم نیست.
برخی میگویند منجمان قدیم حساب کرده بودند که خورشید در هر روز به اندازه محیط دایره جابجا میشود. به همین دلیل یک درجه را بدین صورت تعریف کردند.
نظر دیگری هم هست که بابلیها این واحد را اختراع کردند. واحد شمارش آنها بر مبنای ۶۰ بوده (در حال حاضر بر مبنای ۱۰ است). به همین دلیل به عدد ۳۶۰ رسیدهاند.
همانطور که میبینید، درجه مبنای درستی ندارد. دانشمندان ریاضی به این موضوع پی برده بودند. به همین دلیل سعی کردند واحدی برای زاویه بیابند که عمومی باشد.
در نتیجه رادیان به وجود آمد. پس رادیان واحدی برای اندازهگیری درجه است.
تبدیل رادیان به درجه
[ویرایش]هر رادیان تقریباً برابر با ۵۷ درجه است.به عبارت دیگر هر رادیان برابر درجه است. بنابراین با ضرب در رادیان، درجه به دست میآید. به عبارت دیگر با ضرب زاویه بر حسب رادیان در ۱۸۰ و تقسیم آن بر عدد پی، درجه به دست میآید.
زاویه در درجه = زاویه در رادیان .
به عنوان مثال:
و بلعکس: با ضرب در درجه، رادیان بدست میآید:
جدول زیر تبدیل چند زاویه پرکاربرد را نمایش میدهد:
| درجه | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| رادیان | 0 |
منابع
[ویرایش]ویکیپدیا
گرادیان
در حسابان بردارها گرادیان (به فرانسوی: Gradient) یک میدان نردهای، میدانی برداری است که مؤلفههای آن نرخ تغییر میدان نخستین را در جهتهای مختلف نشان میدهد. جهت خود میدان برداری گرادیان جهت بیشینهٔ تغییرات است.

تعاریف
[ویرایش]تعریف و تعبیر ریاضی-هندسی
[ویرایش]
تعریف و تعبیر فیزیکی-ریاضی
[ویرایش]برداری است در جهت بیشینه آهنگ تغییر فضایی و همواره بر سطح عمود است. مثلاً گرادیان سرعت برابر نیروی محرکه است.
در دستگاه مختصات مختلف
[ویرایش]در دستگاه مختصات دکارتی (کارتزین) گرادیان برابر است با:
و در دستگاه مختصات استوانهای:
و در دستگاه مختصات کروی عبارت است از:
منابع
[ویرایش]ویکی پدیای فارسی
گوه کروی
در هندسه،یک گوه کروی یا یونگولا بخشی از یک توپ است که توسط دو نیمدیسک صاف و یک لون کروی (که به آن قاعده گوه میگویند ) محدود شده است. زاویه بین شعاعهای واقع در نیمدیسکهای مرزی α دو وجهی است . اگر AB نیمه دیسکی است که وقتی به طور کامل حول محور z بچرخد، توپی را تشکیل میدهد ،چرخش AB فقط از طریق α معین،گوهای کروی با همان زاویه α ایجاد میکند.
منابع
[ویرایش]https://en.m.wikipedia.org/wiki/Spherical_wedge
قضیه تالس
قضیه قطع مثلث، که به عنوان قضیه تالس، قضیه تناسب پایه یا قضیه شکافنده جانبی نیز شناخته می شود، یک قضیه مهم در هندسه مقدماتی و اقلیدوسی است که در مورد نسبت های پاره خط های مختلف است که اگر دو خط متقاطع توسط یک جفت موازی قطع شوند، ایجاد می شوند. معادل قضیه نسبت ها در مثلث های مشابه است. این به طور سنتی به تالس ریاضیدان یونانی نسبت داده می شود. بابلیان و مصریان باستان آن را می شناختند، اگرچه اولین اثبات شناخته شده آن در عناصر اقلیدس ظاهر می شود.
منابع
[ویرایش]ریاضی۲پایه یازدهم
ویکی پدیای انگلیسی
ضرب داخلی و خارجی
ضرب داخلی و خارجی بردار، دو اصل مهم در سیستم فضای سه بعدی است.ضرب داخلی و خارجی بردارها را می توان تعمیم داد
قضایا
[ویرایش]قضیه۱=ضرب داخلی دو بردارها همیشه اینگونه نوشته می شوند
(|a|.|b|)=a.b
تعریف ضرب داخلی
[ویرایش]در ریاضیات،ضرب داخلی یا ضرب اسکالر یک عملیات جبری است که دو دنباله اعداد با طول مساوی (معمولاً بردارهای مختصات ) را میگیرد و یک عدد واحد را برمیگرداند. در هندسه اقلیدسی ، حاصل ضرب نقطه ای مختصات دکارتی دو بردار به طور گسترده استفاده می شود.اغلب به آن ضرب درونی (یا به ندرت محصول طرح ریزی ) فضای اقلیدسی می گویند، حتی اگر این تنها محصول درونی نیست که می توان در فضای اقلیدسی تعریف کرد ( برای اطلاعات بیشتر به فضای محصول داخلی مراجعه کنید ).
از نظر جبری، حاصل ضرب نقطه ای مجموع حاصل از ورودی های متناظر دو دنباله اعداد است. از نظر هندسی، حاصل ضرب قدر اقلیدسی دو بردار و کسینوس زاویه بین آنهاست. این تعاریف در هنگام استفاده از مختصات دکارتی معادل هستند. در هندسه مدرن ، فضاهای اقلیدسی اغلب با استفاده از فضاهای برداری تعریف می شوند . در این حالت، حاصل ضرب نقطه برای تعریف طول ها (طول یک بردار، جذر حاصل ضرب نقطه ای بردار به خودی خود است) و زوایا (کسینوس زاویه بین دو بردار، ضریب است) استفاده می شود.حاصل ضرب نقطه آنها با حاصلضرب طول آنها).
تعریف ضرب خارجی
[ویرایش]ضرب خارجی، همچنین ضرب برداری یا ضرب بیرونی ، پیوندی در فضای بردار سه بعدی اقلیدسی است که دوباره یک بردار را به دو بردار اختصاص می دهد. به منظور تمایز آن از سایر محصولات، به ویژه از محصول اسکالر ، در کشورهای آلمانی و انگلیسی زبان با یک malkreuz مشخص شده است. به عنوان علامت ضرب نوشته می شود (به بخش نمادها مراجعه کنید ). واژههای حاصلضرب متقاطع و حاصلضرب بردار به فیزیکدان جوزیا ویلارد گیبس برمیگردد ، اصطلاح محصول بیرونی توسط هرمان گراسمان ابداع شد .
منابع
[ویرایش]https://de.m.wikipedia.org/wiki/Kreuzprodukt
https://en.m.wikipedia.org/wiki/Dot_product
آنالیز حقیقی
آنالیز حقیقی یا آنالیز واقعی یکی از موارد آنالیز ریاضیات است که به مباحث عددهای حقیقی و محاسبات آنها به همراه تغییرات آنها میپردازد. این علم حتی موارد توابع حقیقی را نیز بررسی میکند. آنالیز حقیقی برگرفته از آنالیز مختلط است. چون اعداد حقیقی زیر مجموعه اعداد مختلط است.
محدوده
[ویرایش]ساخت اعداد حقیقی
[ویرایش]قضیه هاب آنالیز واقعی بر اساس ویژگی های سیستم اعداد حقیقی تکیه دارند که حتما باید ایجاد شوند. سیستم اعداد واقعی شامل یک مجموعه غیرقابل شمارش(یعنیR)، همراه با دو عملیات باینری با علامت + و - و یک مرتبه با < . عملیات، اعداد حقیقی را یک فیلد و همراه با ترتیب کردن، یک فیلد مرتب شده حقیقی می سازد. سیستم اعداد واقعی یک فیلد مرتب کامل منحصر به فرد است، به این معنا که هر فیلد مرتب کامل دیگری نسبت به آن هم شکل و شاید متشابه است. به طور شهودی، کامل بودن به این معنی است که هیچ شکافی در اعداد حقیقی وجود ندارد. این ویژگی اعداد واقعی را از سایر فیلدهای مرتب شده متمایز می کند (به عنوان مثال، اعداد گویا[Q]) و برای اثبات چندین ویژگی کلیدی توابع اعداد حقیقی بسیار مهم است. کامل بودن اعداد واقعی اغلب به عنوان ویژگی حداقل کران بالا بیان می شود (به زیر مراجعه کنید).
ترتیب خواص اعداد حقیقی
[ویرایش]این ویژگیهای نظری نظم منجر به تعدادی نتایج اساسی و حقیقی در آنالیز حقیقی میشود، مانند قضیه همگرایی یکنواخت و ساختارهای تکراری آن ، قضیه مقدار متوسط.هر زیر مجموعهR غیر خالی از کران بالایی دارد که دارای حداقل کران بالایی و حدااکثر کران پایینی است که آن هم یک عدد حقیقی است.
با این حال، در حالی که نتایج در آنالیز حقیقی برای اعداد حقیقی بیان می شود، بسیاری از این نتایج را می توان به سایر اشیاء ریاضی تعمیم داد. به طور خاص، بسیاری از ایدهها در آنالیز تابعی و نظریه عملگرها، ویژگیهای اعداد حقیقی را تعمیم میدهند - چنین تعمیمهایی شامل نظریههای فضاهای Riesz و عملگرهای مثبت است . همچنین، ریاضیدانان بخش های واقعی و خیالی توالی های پیچیده را در نظر می گیرند یا با ارزیابی نقطه ای دنباله های عملگر .
کلیات
[ویرایش]ایدههای مختلف از آنالیز حقیقی را میتوان از خط حقیقی به زمینههای گستردهتر یا انتزاعی تر تعمیم داد. این تعمیمها آنالیز حقیقی را به سایر رشتهها و زیرشاخهها پیوند میزند. به عنوان مثال، تعمیم ایدههایی مانند توابع پیوسته و فشردگی از تحلیل واقعی به فضاهای متریک و فضاهای توپولوژیکی، تحلیل واقعی را به حوزه توپولوژی عمومی متصل میکند، در حالی که تعمیم فضاهای اقلیدسی محدود به آنالوگهای بیبعد منجر به مفاهیم فضاهای باناخ و فضاهای هیلبرت و به طور کلی به تحلیل عملکردی میشود.
جورج کانتور بررسی مجموعهها و توالی اعداد حقیقی، نگاشت بین آنها و مسائل اساسی تحلیل واقعی، نظریه مجموعههای سادهلوحانه را به وجود آورد. مطالعه مسائل مربوط به همگرایی برای دنبالهای از توابع در نهایت منجر به تجزیه و تحلیل فوریه به عنوان زیرشاخهای از آنالیز ریاضی شد. بررسی پیامدهای تعمیم تمایزپذیری از توابع یک متغیر واقعی به یک متغیر مختلط، مفهوم توابع هولومورفیک و شروع تحلیل پیچیده را به وجود آورد. از سوی دیگر، تعمیم ادغام از مفهوم ریمان به معنای لبگ منجر به تدوین مفهوم فضاهای اندازهگیری انتزاعی شد که یک مفهوم اساسی در نظریه اندازهگیری است. در نهایت، تعمیم ادغام از خط حقیقی به منحنیها و سطوح در فضای ابعاد بالاتر (فضای سه بعدی)، باعث مطالعه حساب برداری شد که تعمیم و رسمیسازی بیشتر آن نقش مهمی در تکامل مفاهیم اشکال دیفرانسیل و منیفولدهای (؟) صاف (متمایز) ایفا کرد. در هندسه دیفرانسیل و سایر حوزههای هندسه نزدیک به هم وتوپولوژی این مبحث کاربردهای زیادی دارد، چون در آنالیز حقیقی در مختصاتهای هندسه دیفرانسیل، در نمادهای خاصیتی توپولوژی استفاده میگردد، آنالیز حقیقی در توابع استفاده نیز میگردد و تابع را براساس انتگرال به همراه قانون تابع و مختصاتهای تابعی استفاده میگردد
منابع
[ویرایش]ویکی پدیای انگلیسی
آنالیز مختلط
آنالیز مختلط که در گذشته به عنوان نظریه توابع یک متغیر مختلط شناخته میشد، شاخهای از آنالیز ریاضی است که به بررسی توابع اعداد مختلط میپردازد. در بسیاری از شاخههای ریاضیات از جمله هندسه جبری، نظریه اعداد، ترکیبات تحلیلی و ریاضیات کاربردی مفید است؛ و همچنین در فیزیک از جمله شاخههای هیدرودینامیک، ترمودینامیک و به ویژه مکانیک کوانتومی. با گسترش، استفاده از تجزیه و تحلیل پیچیده در زمینههای مهندسی مانند مهندسی هستهای، هوافضا، مکانیک و برق نیز مورد استفاده قرار میگیرد. از آنجایی که یک تابع قابل تمایز یک متغیر مختلط برابر با سری تیلور آن است (یعنی تحلیلی است)، تجزیه و تحلیل پیچیده به ویژه به توابع تحلیلی یک متغیر مختلط (یعنی توابع هولومورفیک) مرتبط است.
تاریخ
[ویرایش]آنالیز پیچیده یکی از شاخههای کلاسیک ریاضیات است که ریشه در قرن هجدهم و کمی قبل از آن دارد. ریاضیدانان مهم مرتبط با اعداد مختلط عبارتند از: اویلر، گاوس، ریمان، کوشی، وایرشتراس و بسیاری دیگر در قرن بیستم. تجزیه و تحلیل پیچیده، به ویژه تئوری نقشههای همگام، کاربردهای فیزیکی زیادی دارد و همچنین در سراسر نظریه اعداد تحلیلی استفاده میشود. در دوران مدرن، از طریق بهبود جدید دینامیک پیچیده و تصاویر فراکتالها که با تکرار توابع هولومورفیک تولید میشوند، بسیار محبوب شده است. یکی دیگر از کاربردهای مهم آنالیز پیچیده در نظریه ریسمان است که به بررسی متغیرهای همسان در نظریه میدان کوانتومی میپردازد.
مفاهیم و قضیههای اساسی
[ویرایش]تابع مختلط
[ویرایش]
این توابع به ویژه در مطالعه هندسه فراکتال ها و علوم مهندسی مانند طراحی مدارها و سیستم های مختلف الکترونیکی و مخابراتی کاربرد زیادی دارند. برخلاف توابع واقعی، توابع پیچیده نمی توانند به صورت هندسی روی صفحه نمایش داده شوند و دو بعدی هستند. راه های مختلفی برای نمایش اعداد مختلط وجود دارد. یکی از راه های نمایش این اعداد استفاده از روش دکارتی است. روش دوم نمایش این اعداد، نمایش استاندارد است. سومین و مهمترین روش نمایش اعداد مختلط نمایش قطبی است. فرمول اویلر، ریاضیدان معروف سوئیسی، نقش کلیدی در نمایش اعداد مختلط به شکل قطبی دارد.
مشتقپذیری
[ویرایش]
فرمول کوشی
[ویرایش]
ماندهها
[ویرایش]بسط دادن
[ویرایش]بر خلاف، توابع حقیقی، بسط تیلور برای توابع تحلیلی، همیشه امکانپذیر است. از این گذشته، در شرایط خاصی نیز میتوان از بسط لورنتس در این تئوری استفاده کرد.
منابع
[ویرایش]ویکی پدیا فارسی
آنالیز تابعی

آنالیز تابعی شاخه ای از تحلیل ریاضی است که فضاهای برداری مجهز به ساختارهای مربوط به حد (مانند ضرب درونی، صاف، توپولوژی و غیره) و توابع خطی را که بر روی این فضاها تعریف می شوند (و با ساختار مذکور در ارتباط هستند) مطالعه می کند. به روشی مناسب) هسته آن را تشکیل می دهند. ریشههای تاریخی تحلیل تابعی در مطالعه فضاهای تابع و فرمولبندی ویژگیهای تبدیلهای تابعی مانند تبدیل فوریه است. چنین تبدیل هایی عملگرهای پیوسته، واحد و غیره را بین فضاهای تابع تعریف می کنند.
تجزیه و تحلیل تابع
[ویرایش]کلمه تابع (یا تابعک) ریشه در حساب تغییرات دارد و به معنای تابعی است که ورودی آن تابع است. این اصطلاح اولین بار توسط هادامارد در کتاب خود در سال ۱۹۱۰ که با همین موضوع نوشته شده است به کار رفت. با این حال، مفهوم کلی زیرنویس قبلاً در سال ۱۸۸۷ توسط ریاضیدان و فیزیکدان ایتالیایی ویتو ولترا استفاده شد. تئوری زیرمجموعههای غیرخطی توسط شاگردان هادامارد به ویژه فرشه و لوی ادامه یافت. همچنین هادامارد مکتب مدرن تجزیه و تحلیل توابع خطی را پایهگذاری کرد که پس از او توسط ریس و گروهی از ریاضیدانان لهستانی در اطراف استفان باناخ توسعه یافت و ادامه یافت.
کتب مقدماتی تابع
[ویرایش]در کتب مدرن تحلیل عملکردی این مبحث به عنوان بررسی فضاهای برداری مجهز به توپولوژی در نظر گرفته شده است که یکی از ویژگی های خاص آنها بعد بی نهایت است. اگر بخواهیم آنالیز تابعی را با جبر خطی مقایسه کنیم، جبر خطی به طور کلی با فضاهای با ابعاد محدودی که از توپولوژی استفاده نمی شود، سروکار دارد. بخش مهمی از تحلیل تابعی، توسعه قضایای مربوط به تئوری اندازه، انتگرال گیری و احتمالات به فضاهای ابعادی نامتناهی است که به آن تحلیل ابعادی نامتناهی نیز می گویند.
منابع
[ویرایش]ویکی پدیای فارسی
آنالیز هارمونیک

آنالیز هارمونیک شاخه ای از ریاضیات است که مرتبط با نمایش توابع یا سیگنالها به صورت برآیندی از امواج پایه بوده و به مطالعه و نمایش مفاهیم سریهای فوریه و تبدیل فوریه (یعنی فرم توسعه یافتهی آنالیز فوریه) میپردازد. در دو قرن اخیر، این شاخه به شاخهای وسیع تبدیل شده که کاربردهای گستردهای در نظریه اعداد، نظریه نمایش، پردازش سیگنال، مکانیک کوانتومی، آنالیز جزر و مدی و علوم اعصاب دارد.
عبارت "هماهنگها" از ریشه یونانی به معنای "ماهر در موسیقی" گرفته شده است.در مسائل فیزیکی مقدار ویژهای، این که فرکانس یک موج ضرایب صحیحی از موج دیگری باشد، معنادار شد، مثل هماهنگهای نوت های موسیقایی، اما این اصطلاح (هماهنگ) کاربردهایی فراتر از معنی اصلی آن پیدا کرد.
تبدیل فوریه کلاسیک روی هنوز هم یک حوزه زنده تحقیقاتیست، بخصوص تبدیلهای فوریه روی اشیای کلیتری چون توزیعات تمپرد. به عنوان مثال، اگر ما برخی الزامات روی توزیعی چون اعمال کنیم، میتوانیم آن ها را به زبان تبدیل فوریه روی نیز ترجمه کنیم. قضیه پالی-وینر مثالی از این فرایند است. قضیه پالی-وینر فوراً ایجاب می کند که اگر یک توزیع ناصفر با تکیهگاهی فشرده باشد (شامل توابع با تکیهگاه ثابت هم میشود)، آنگاه تبدیل فوریه آن هیچگاه تکیه گاه فشرده نخواهد داشت. این حالت بسیار مقدماتی از اصل عدم قطعیت در بستر آنالیز-هارمونیک است.
سریهای فوریه را میتوان در بستر فضاهای هیلبرت بهطور مناسبتری مطالعه کرد، چرا که در آنجا ارتباطی بین آنالیز هارمونیک و آنالیز تابعی ارائه میکند.
منابع
[ویرایش]ویکی پدیای فارسی
آنالیز پیچیده
آنالیز مختلط که به طور سنتی به عنوان نظریه توابع یک متغیر مختلط شناخته می شود، شاخه ای از آنالیز ریاضی است که به بررسی توابع اعداد مختلط می پردازد. در بسیاری از شاخه های ریاضیات از جمله هندسه جبری ، نظریه اعداد ، ترکیبات تحلیلی ، ریاضیات کاربردی مفید است . و همچنین در فیزیک , از جمله شاخه های هیدرودینامیک , ترمودینامیک , و به ویژه مکانیک کوانتومی . با گسترش، استفاده از تحلیل پیچیده در زمینه های مهندسی نیز کاربرد داردمهندسی هسته ای , هوافضا , مکانیک و برق .
از آنجایی که یک تابع قابل تمایز یک متغیر مختلط با سری تیلور آن برابر است (یعنی تحلیلی است )، تحلیل مختلط به ویژه به توابع تحلیلی یک متغیر مختلط (یعنی توابع هولومورفیک ) مربوط می شود.
تاریخ
[ویرایش]آنالیز پیچیده یکی از شاخه های کلاسیک ریاضیات است که ریشه در قرن هجدهم و کمی قبل از آن دارد. ریاضیدانان مهم مرتبط با اعداد مختلط عبارتند از: اویلر، گاوس، ریمان، کوشی، وایرشتراس و بسیاری دیگر در قرن بیستم. تجزیه و تحلیل پیچیده، به ویژه تئوری نقشه های همگام، کاربردهای فیزیکی زیادی دارد و همچنین در سراسر نظریه اعداد تحلیلی استفاده می شود. در عصر مدرن، از طریق افزایش جدید دینامیک پیچیده و تصاویر فراکتال تولید شده با تکرار توابع هولومورف، بسیار محبوب شده است. یکی دیگر از کاربردهای مهم تحلیل پیچیده در نظریه ریسمان است که متغیرهای یکسان را در نظریه میدان کوانتومی بررسی می کند.
تابع پیچیده
[ویرایش]تابع مختلط تابعی از اعداد مختلط به اعداد مختلط است. به عبارت دیگر تابعی است که زیر مجموعه ای از اعداد مختلط به عنوان دامنه و اعداد مختلط به عنوان کد دامنه دارد. توابع پیچیده معمولاً دامنه ای دارند که شامل یک زیر مجموعه باز غیر خالی از صفحه مختلط است.
برای هر تابع پیچیده، مقادیرz از دامنه و تصاویر آنهادر محدوده تابع (f(z را می توان به بخش های واقعی و خیالی تقسیم کرد :
جایی کههمه دارای ارزش واقعی هستند.
به عبارت دیگر، یک تابع پیچیدهممکن است تجزیه شود
و
می توان به عنوان مثال، به دو تابع با ارزش واقعی () از دو متغیر واقعی ()باشد.
به طور مشابه، هر تابع با مقادیر مختلط f در مجموعه دلخواه X را می توان به عنوان یک جفت مرتب از دو تابع با ارزش واقعی در نظر گرفت : (Re f , Im f ) یا به عنوان یک تابع با مقدار برداری از X بهR2.
برخی از ویژگی های توابع با ارزش پیچیده (مانند پیوستگی) چیزی بیش از ویژگی های متناظر توابع با ارزش برداری دو متغیر واقعی نیستند. سایر مفاهیم تحلیل پیچیده، مانند تمایزپذیری، تعمیم مستقیم مفاهیم مشابه برای توابع واقعی هستند، اما ممکن است ویژگی های بسیار متفاوتی داشته باشند. به طور خاص، هر تابع پیچیده قابل تمایز، تحلیلی است (به بخش بعدی مراجعه کنید)، و دو تابع متمایز که در همسایگی یک نقطه برابر هستند، در تقاطع دامنه های خود برابر هستند (اگر دامنه ها به هم متصل باشند). ویژگی اخیر اساس اصل تداوم تحلیلی است، که اجازه می دهد تا هر تابع تحلیلی واقعی را به روشی منحصر به فرد گسترش دهیم تا یک تابع تحلیلی پیچیده به دست آوریم که دامنه آن کل صفحه پیچیده با تعداد محدودی از کمان های منحنی حذف شده است گسترش دهد وبه حد نصاب برساند. بسیاری از توابع پیچیده اساسی و ویژه به این ترتیب تعریف می شوند که شامل توابع نمایی پیچیده، توابع لگاریتمی پیچیده و توابع مثلثاتی می شود.
منابع
[ویرایش]ویکی پدیای انگلیسی
آنالیز عددی
آنالیز عددی به تنظیم، مطالعه، و اعمال شیوههای تقریبی محاسباتی برای حلّ آن دسته از مسائل ریاضیات پیوسته (در مقابل ریاضیات گسسته) میپردازد که با روشهای تحلیلی و دقیق قابل حلّ نیستند. برخی از مسائل مورد نظر محاسبات عددی بهطور مستقیم از حسابان میآید. جبر خطی عددی (بر روی میدانهای حقیقی یا مختلط) و نیز حلّ معادلات دیفرانسیل خطی و غیر خطی مربوط به فیزیک و مهندسی از جملهٔ زمینههای دیگر برای کاربرد محاسبات عددیست.
تاریخچه
[ویرایش]از آثار مکتوب بهجامانده چنین برمیآید که گویا نخستین رساله در حساب به معنی امروزی را محمد بن موسی الخوارزمی نوشتهاست. آوازهٔ وی چنان در اروپا پیچید که واژهٔ الگوریتم را (که از الخوارزمی گرفته شدهاست) بر روشهای حل مسئله در محاسبات عددی نهادند.
با پیشرفت رایانهها نیاز به حل مسایل ریاضی به روش عددی بیش از پیش احساس شد. در این هنگام کارایی روشهایی که از قبل توسط نیوتون و لئونارد اویلر ارائه شده بود نمایان شد. ریاضیکارها و دانشگرهای دیگر نیز در این راه پا گذاشتند و روشهایی کاراتر ارائه دادند. به این ترتیب محاسبات عددی شکل نوین خود را یافت.
معرفی
[ویرایش]تعدادی از مسائل ریاضیات پیوسته دقیقاً با یک الگوریتم حل میشوند که به روشهای مستقیم حل مسئله معروفاند. برای مثال، روش حذف گوسی برای حل دستگاه معادلات خطی، و نیز الگوریتم غیرمرکب مورد استفاده در برنامهریزی خطی را میتوان ذکر نمود. در مقابل، برای بسیاری از مسائل روش حل مستقیم وجود ندارد و باید از روشهای دیگری مانند روش تکرارشونده استفاده شود.
برآورد خطاها
[ویرایش]تخمین خطاهای موجود در حل مسائل از مهمترین قسمتهای محاسبات عددی است این خطاها در روشهای تکرارشونده وجود دارد چون به هرحال جوابهای تقریبی بهدست آمده با جواب دقیق مسئله، اختلاف دارد یا وقتیکه از روشهای مستقیم برای حل مسئله استفاده میشود خطاهایی ناشی از گرد کردن اعداد بهوجود میآید. در محاسبات عددی میتوان مقدار خطا را درآخر روش که برای حل مسئله به کار میرود، تخمین زد.
کاربردها
[ویرایش]الگوریتمهای مربوط به محاسبات عددی در حل بسیاری از مسائل موجود در علوم و مهندسی مورد استفاده قرار میگیرد. به عنوان مثال :
- تحلیل و طراحی سازههایی همچون پلها، سدها، و هواپیماها
- هواشناسی مثلاً پیشبینی آب و هوا، و تهیه نقشههای جوی از زمین
- تجزیه و تحلیل ساختار مولکولها
- پیدا کردن مخازن
- مدل سازی چند مقیاسی ریه با روشهای محاسباتی و بررسی عملکرد ریه و عوامل مؤثر بر آسم
- مدل سازی ریاضی تحرکات و رفتارهای جانوران از طریق تحلیل عددی معادلات دیفرانسیل مربوطه
- دینامیک چرخهها و شبکههای هتروکلینیک با روشهای محاسباتی
- توموگرافی امپدانس الکتریکی
- توموگرافی توزیع اپتیکی
- منیفلد (؟؟؟؟؟)سامانههای چندمقیاسی زمانی
- مدل سازی چند مقیاسی ترشح بزاق و تحلیلهای عددی مربوطه
- دینامیک سیستمها با مقیاس زمانی چندمقیاسی
- مسائل معکوس بیزی
- انتشار موج محاسباتی
- مدل سازی و حل عددی حرکت و تعاملات سلولهای ایمنی
- تحریک پذیری ذاتی و سایر اثرات گذرا
- دینامیک مدلهای آب و هوایی
- دینامیک گردابه پایداری گردابه
- ریاضیات صنعتی: توموگرافی فرایند
- پردازش تصویربرداری در صنایع شیمیایی، صنایع خمیر و کاغذ و صنایع معدنی.
- دینامیک مدلهای اقلیمی و پیش بینی تغییرات آب و هوایی با استفاده از مدل سازی و تحلیل عددی
همچنین اکثر ابررایانهها بهطور مداوم بر اساس الگوریتمهای محاسبات عددی برنامهریزی میشوند. بهطور کلی محاسبات عددی از نتایج عملی حاصل از اجرای محاسبات برای پیدا کردن روشهای جدید برای تجزیه و تحلیل مسائل استفاده میکند.
منابع
[ویرایش]ویکی پدیای فارسی
آنالیز برداری
تجزیه و تحلیل برداری یک کتاب درسی توسط ادوین بیدوول ویلسون است که برای اولین بار در سال ۱۹۰۱ منتشر شد و بر اساس سخنرانیهایی است که جوزایا ویلارد گیبز در مورد این موضوع در دانشگاه ییل ارائه کرده بود. این کتاب برای استاندارد کردن نمادها و واژگان جبر خطی سه بعدیو حساب برداری که توسط فیزیکدانان و ریاضیدانان استفاده میشود، بسیار کمک کرد. این اثر در سالهای ۱۹۱۳، ۱۹۱۶، ۱۹۲۲، ۱۹۲۵، ۱۹۲۹، ۱۹۳۱ و ۱۹۴۳ توسط ییل تجدید چاپ شد. این اثر اکنون در مالکیت عمومی است. در سال ۱۹۶۰ توسط انتشارات دوور تجدید چاپ شد.
فهرست
[ویرایش]این کتاب دارای عنوان فرعی است "کتاب درسی برای استفاده دانشجویان ریاضی و فیزیک؛ که بر اساس سخنرانیهای جی. ویلارد گیبز، دکترا، LL.D." فصل اول بردارها را در سه بعد فضایی، مفهوم اسکالر (واقعی) و حاصل ضرب یک اسکالر با بردار پوشش میدهد. فصل دوم محصولات نقطهای و متقاطع را برای جفت بردارها معرفی میکند. اینها به یک محصول سهگانه اسکالر و یک محصول چهارگانه گسترش مییابد. صفحات ۷۷ تا ۸۱ اصول مثلثات کروی را پوشش میدهد، موضوعی که در آن زمان به دلیل استفاده از آن در جهت یابی آسمانی مورد توجه بود.. فصل سوم نماد حساب بردار بر اساس عملگر del را معرفی میکند. تجزیه هلمهولتز یک میدان برداری در صفحه ۲۳۷ آورده شده است.
هشت صفحه پایانی دو بردارها را توسعه میدهند، زیرا این دو جزء لاینفک درس نظریه الکترومغناطیسی نور است که پروفسور گیبز در ییل تدریس کرد. ابتدا ویلسون یک دوبردار را با یک بیضی مرتبط میکند. حاصل ضرب دو بردار با عدد مختلط روی دایره واحد، چرخش بیضوی نامیده میشود. ویلسون با توصیف حرکت هارمونیک بیضوی و مورد امواج ساکن ادامه میدهد.
منابع
[ویرایش]ویکیپدیای انگلیسی
دستهبندی دادهها
دستهبندی داده ها،نوعی کمیت در علمآمار است که داده های بیش از۱۰تا را محاسبه میکند و مجموعههایی از چنددسته را ایجاد میکند
این دستهبندی حتی میانگین بیش از۱۰تا داده را محاسبه میکند
این مبحث در ریاضیات کاربردی در موضوع علمآمار به موارد دستهبندی قد ها در متوسط،کوتاه،بلند،سود و زیان در اقتصاد و مالیات و... بسیار خوب است.
تعاریف
[ویرایش]دامنه تغییرات
[ویرایش]به اختلاف دوعدد که یکیاز آن بزرگترین داده باشد و یکیدیگر کوچکترین داده باشد دامنه تغییرات گفته میشود.
دسته ها
[ویرایش]به تعداد دستههای مشخص در دستهبندی ها که نوعیمتغیر به حساب میآید گفته میشود که اختلاف دو داده بزرگترین و کوچکترین را به تعداد آن تقسیم میکند.ایندسته نشان میدهد کدام داده درمحدوده خود دستهبندی شوند.
فراوانی
[ویرایش]حاصل جمعآوری یکدسته درمحدود دستهرا گویند کهچندین داده در مجموعه قرار دارد.
مرکز دسته
[ویرایش]مرکز دسته یعنی میانگین دو محدوه دسته که برابر با مجموع آنها بر تقسیم عدد دو که برای میانگین داده ها به کار می رود.
منابع
[ویرایش]ریاضیات پایه هشتم/چاپ هشتم/۱۴۰۰
قانون احتمال کل
در احتمال یک قاعده اساسی است که احتمالات حاشیه ای را به احتمالات شرطی مرتبط می کند و این احتمال کل یک نتیجه را بیان می کند که می تواند از طریق چندین رویداد متمایز تحقق یابد ، از این رو نام آن قانون احتمال کل است.
در آمار و احتمال قانون احتمال کل به روش زیر بیان میشود.
که احتمال شرطی[یادداشت ۱] A است در صورتی که N دانسته شده باشد.
قانون گزینهها
[ویرایش]حالت خاص قانون احتمال کامل، قانون گزینههاست که در متغیرهای تصادفی گسسته معتبر است. این قانون میگوید اگر { Bn: n = 1, 2, 3, ... }حاصل از تقسیم فضای احتمال B بر n قسمت متنهای یا نامتنهای و قابل شمارش باشد، و هر 'Bn قابل شمارش باشد. آنگاه:
یا به بیان دیگر:
افراز
[ویرایش]فرض کنید مجموعه U را میخواهیم به زیرمجموعههایی تقسیم کنیم. در اینصورت داریم:

قانون افراز
[ویرایش]برای افرازها و مجموعه کل یک سری قوانین وجود دارد که شامل عبارت های زیر است:
افراز در پرتاب سکه
[ویرایش]پیشامد[یادداشت ۲] رو آمدن را با و پیشامد پشت آمدن را با نشان میدهیم.
فضای نمونه[یادداشت ۳] برابر است با:
حالا شرطهای افراز میبینیم:
یادداشت
[ویرایش]- ↑ در نظریه احتمال ، احتمال شرطی معیاری از احتمال وقوع یک رویداد است، با توجه به اینکه رویداد دیگری (با فرض، فرض، ادعا یا شواهد) قبلاً رخ داده است. این روش خاص متکی بر رویداد B است که با نوعی رابطه با یک رویداد دیگر A رخ می دهد. در این رویداد، رویداد B را می توان با یک احتمال مشروط نسبت به A تجزیه و تحلیل کرد. اگر رویداد مورد علاقه A و رویداد باشد. B شناخته شده است یا فرض می شود که رخ داده است، "احتمال شرطی A داده شده B "، یا "احتمال A تحت شرطB "، معمولاً به صورت (P( A | B یا گاهی اوقات (PB(A نوشته می شود.
- ↑ در نظریهی احتمالات ،پیشامد مجموعهای شامل برخی نتایج ممکن برای آزمایشی تصادفی است که زیرمجموعهای از فضای نمونه میباشد. اگر برآمد(نتیجه، خروجی) یک آزمایش در پیشامد Eوجود داشتهباشد میگوییم پیشامدEرخ دادهاست. برآمد حاصل از یک آزمایش میتواند عضو پیشامدهای متعددی باشد. همچنین پیشامدهای مختلفی میتوانند روی یک آزمایش تعریف شوند که لزوماً احتمال وقوع آنها یکسان نیست؛ زیرا هر کدام میتوانند شامل گروههای مختلفی از برآمدها باشند.
- ↑ در نظریه احتمال فضای نمونه یا فضای نمونهای مجموعه تمام نتایج ممکن از یک آزمایش تصادفی (پدیده تصادفی) است که آن را با نماد،یا نشان میدهند. پیامد هر آزمایش تصادفی، تنها یکی از اعضای خواهد بود. به عنوان مثال، برای آزمایش پرتاب سکه، فضای نمونه برابر است با مجموعه {شیر، خط} و برای یک تاس شش وجهی، فضای نمونه برابر است با مجموعه {۱، ۲، ۳، ۴، ۵، ۶}. در یک رویکرد ساده به احتمالات، هر زیر مجموعهای از فضای نمونه را میتوان یک پیشامد نامید. با این حال، این تعریف زمانی که فضای نمونه نامتناهی باشد مشکلساز میشود. در یک تعریف بهتر، پیشامد را یک زیرمجموعهٔ قابلاندازهگیری از فضای نمونه در نظر میگیرند که شامل یک میدان سیگما روی فضای نمونه باشد.
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
میانگین
چندین گونه برای میانگین (به انگلیسی: Mean) در ریاضیات و بهویژه در آمار وجود دارد. در مطالعه توزیع یک جامعه آماری مقدار نماینده که اندازهها در اطراف آن توزیع شدهاند را مقدار مرکزی مینامند و هر معیار عددی را که معرف مرکز مجموعه دادهها باشد، معیار گرایش به مرکز مینامند. میانگین و میانه از متداولترین معیارهای گرایش به مرکز هستند.
انواع
[ویرایش]میانگین در ریاضیات و آمار کاربرد متفاوت دارد، که شامل
- میانگین حسابی، میانگین حسابی به این شکل تعریف میشود:
- مثال: میانگین حسابی برابر است با
- میانگین هندسی، میانگین هندسی به این شکل تعریف میشود:
- مثال: میانگین هندسی برابر است با
- میانگین هارمونیک، میانگین هارمونیک به این شکل تعریف میشود:
- مثال میانگین هارمونیک برابر است با
- و در آمار به امید ریاضی که یک متغیر تصادفی است و همچنین میانگین جامعه آماری نامیده میشود.
میانگینهای دیگری نیز در دانشهای گوناگون کاربرد دارند که از میان شناختهشدهترین آنها میتوان میانگین وزنی را نام برد.
میانگین بیش از ۱۰ داده
[ویرایش]برای محاسبه میانگین بیش از ده داده، باید به صورت جدول فراوانی آنها را پیدا کرد.
ضرب مرکز دسته در فراوانی و مجموعه آنها و تقسیم بر تعداد دادهها میانگین به دست میآید.
مثال
[ویرایش]۳۰ دانش آموز در کلاس نهم نمرات ریاضی مختلفی گرفتند و معلم میخواهد با دستهبندی ۸ تایی و باتوجه به نمرات ریاضی دانش آموزان، میانگین نمرات را محاسبه کند. میانگین نمرات دانش آموزان چقدر است؟ (نمرات از ۱۰۰ نمره است)
نمرات:۳۰٬۴۰٬۱۲٬۴۵٬۶۷٬۸۹٬۷۸٬۴۸٬۹۳٬۱۲٬۹٬۴٬۲۳٬۵۶٬۸٬۵٬۴۵٬۶۷٬۲۴٬۸۴٬۸۲٬۷۴٬۴۶٬۴۱٬۹۰٬۱۰۰٬۳۴٬۸۹٬۵۰٬۸۰٬۸۱
حل مسئله
[ویرایش]طبق جدول فراوانی میانگین را محاسبه میکنیم.
ابتدا داده کمترین و بیشترین را پیدا میکنیم:۴٬۱۰۰
دامنه تغییرات برابر است با:۹۶
چون دستهبندی ها۸تا است پس جدول را به ۸ قسمت تقسیم میکنیم
| مرکز×فراوانی | مرکز دسته | فروانی | محدوده دسته |
|---|---|---|---|
مجموع مرکز×فراوانی=۱۵۴۸
میانگین:51.6
پس میانگین برابر با۵۱٫۶است.
منابع
[ویرایش]ویکی پدیای فارسی
ریاضی پایه هشتم
متغیرهای آمار
متغیرهای آمار، نوعی از متغیرهاهستند،که بسیار در آمار کاربرد دارد. متغیرهای آمار در مورد موارد طبیعی آمار را در زندگی انجام می دهد. این نوع متغیرها در ریاضی به دلیل اینکه موارد گونانی را در زندگی دارد، اسمشان متغیر هست یا واحد های یکسانی داشته باشد.
انواع متغیرها
[ویرایش]متغیرها به دونوع تقسیم می شوند
- متغیر کمی
- متغیر کیفی
متغیرهای کمی و کیفی هم به دو دسته تقسیم می شوند.
متغیرهای کمی
- متغیر کمی گسسته
- متغیر کمی پیوسته
متغیرهای کیفی
- متغیر کیفی ترتیبی
- متغیر کیفی اسمی
تعاریف
[ویرایش]متغیرهای کمی
[ویرایش]متغیرهای هستند که بیان کننده کمیت و اندازه می باشند و می توان آنها را به دسته گسسته و پیوسته تقسیم نمود.
متغیر کمی گسسته
[ویرایش]متغیرهایی که فقط قابل شمارش هستند، متغیرهای گسسته می گوییم.
متغیر کمی پیوسته
[ویرایش]متغیرهایی که اندازه پذیرند و مقادیر آنها در فاصله ای از اعداد حقیقی قرار دارد متغیرهای پیوسته می گوییم.
متغیرهای کیفی
[ویرایش]متغیرهای هستند که بیان کننده حالت و کیفیت می باشند و شامل متغیرهای اسمی و رتبه ای است
متغیرهای کیفی اسمی
[ویرایش]این مقیاس به داده ها یا اطلاعاتی در مورد صفتها یا ویژگیهایی دلالت دارند. که نمیتوان بصورت عددی و عملیات ریاضی و آماری بر آنها انجام داد. در طبقه بندی اسمی دادهها را بر اساس صفتی یا ویژگی گروهبندی میکنند. این طبقهها یا گروهها با همدیگر رابطه ضروری ندارند.در این طبقه بندی طبقه ها از هم جدا هستند. به هر یک از طبقه ها میتوان عددی را اختصاص داد، اما این عدد ارزش کمی یا مقداری نداشته و تابع قوانین ریاضی نیست. برای مثال میتوان در ورود دادههای مربوط به جنسیت در نرم افزارهای آماری کد شماره یک را به مرد اختصاص داد و کد شماره دو را به زن اختصاص داد.
متغیرهای کیفی ترتیبی
[ویرایش]این نوع مقیاس در خصوص دادههایی میباشد که بر اساس یک نظام سلسلهای ترتیب بندی یا رتبه بندی می شوند. این مقیاس، علاوه بر این که خصوصیات متغیر اسمی را دارا میباشد از ویژگی ترتیبی نیز برخوردار است. رتبهها را میتوان با روشهای گوناگون آماری با هم مقایسه کرد. ولی آنها ارزش عددی ندارند. ارزش آنها در ارتباط یا تناسب با رتبههای دیگر مشخص می شود. در این نوع مقیاس رتبه بندی از عدد کم به بالا انجام می گیرد. برای مثال اگر دانش آموزی بالاترین نمره را کسب کند به عنوان شاگرد اول در نظر گرفته میشود. به عبارت دیگر بالاترین رتبه همیشه یک خواهد بود و تفاوت بین یک رتبه با رتبه بعدی نیز بدون توجه به مقدار صفت یا ویژگی مورد نظر همیشه یک در نظر گرفته میشود.
منابع
[ویرایش]
آمار استنباطی
استنباط آماری فرآیند استفاده از تجزیه و تحلیل داده ها برای استنتاج ویژگی های توزیع احتمال اساسی است. تحلیل استنتاج آماری در مورد ویژگی های جامعه نتیجه گیری می کند و برای این نتیجه گیری از آزمون فرضیه ها و استنباط تخمین ها استفاده می کند. در اینجا، فرض بر این است که مجموعه داده مشاهده شده از یک جمعیت بزرگتر نمونه برداری شده است.
اگر به جای مطالعه کل جامعه، بخشی از آن با استفاده از تکنیک های نمونه گیری انتخاب و مطالعه شود و بخواهیم نتایج را به کل جامعه تعمیم دهیم، از روش هایی استفاده می شود که موضوع آمار استنباطی است. آنچه مهم است این است که در گذر از آمار توصیفی به آمار استنباطی یا به عبارتی از نمونه به جامعه، بحث و نقش احتمال آغاز می شود. در واقع، احتمال پل ارتباطی بین آمار توصیفی و استنباطی است.
مقدمه ای برای بررسی
[ویرایش]استنباط آماری با استفاده از دادههای جمعآوریشده با نوعی نمونهگیری، گزارههایی را درباره یک جمعیت ارائه میکند. با توجه به فرضیه ای در مورد یک جامعه، که می خواهیم برای آن استنتاج کنیم، استنتاج آماری شامل (اول) انتخاب یک مدل آماری از فرآیند است که داده ها را تولید می کند و (دوم) استنتاج گزاره هایی از مدل.
کونیشی و کیتاگاوا بیان می کنند،(اکثر مسائل در استنتاج آماری را می توان مسائل مربوط به مدل سازی آماری در نظر گرفت.)در همین رابطه، سر دیوید کاکس گفته است: "نحوه ترجمه از مسئله موضوعی به مدل آماری اغلب به این صورت است. مهم ترین بخش یک تحلیل».
نتیجه گیری یک استنتاج آماری یک گزاره آماری است.برخی از اشکال رایج گزاره های آماری به شرح زیر است:
- یک تخمین نقطه ای، یعنی مقدار خاصی که به بهترین وجه برخی از پارامترهای مورد علاقه را تقریب می کند.
- تخمین بازه ای، به عنوان مثال یک فاصله اطمینان (یا برآورد مجموعه)، یعنی فاصله ای که با استفاده از مجموعه داده ای که از یک جمعیت گرفته شده است، ساخته شده است، به طوری که، تحت نمونه برداری مکرر از چنین مجموعه های داده، چنین بازه هایی حاوی مقدار پارامتر واقعی با احتمال در سطح اطمینان اعلام شده باشد.
- یک فاصله معتبر، یعنی مجموعه ای از ارزش ها که مثلاً 95 درصد از باورهای پسین را شامل می شود.
- رد یک فرضیه ضعیف
- خوشه بندی یا طبقه بندی نقاط داده در گروه ها.
مدل ها و مفروضات
[ویرایش]هر گونه استنباط آماری مستلزم برخی مفروضات است. مدل آماری مجموعه ای از مفروضات مربوط به تولید داده های مشاهده شده و داده های مشابه است. توصیف مدلهای آماری معمولاً بر نقش مقادیر جمعیت مورد علاقه تأکید میکند که میخواهیم درباره آن استنباط کنیم.آمار توصیفی معمولاً به عنوان یک مرحله مقدماتی قبل از استنتاج رسمی بیشتر استفاده می شود.
منابع
[ویرایش]ویکی پدیای فارسی
ویکی پدیای انگلیسی
آمار توصیفی
موضوع آمار توصیفی، موضوع چیدمان و طبقهبندی دادهها، نمایش گرافیکی و محاسبه مقادیری مانند میانگین، میانه، میانه و غیره است که به ویژگیهای هر یک از اعضای جامعه مورد بحث اشاره دارد. در آمار توصیفی، اطلاعات به دست آمده از یک گروه، همان گروه را توصیف می کند و اطلاعات به دست آمده را نمی توان به گروه های مشابه تعمیم داد.
روش ها
[ویرایش]به طور کلی در آمار توصیفی برای جمع بندی داده ها از سه روش استفاده می شود:
- استفاده از جداول
- استفاده از نمودار
- محاسبه مقادیری خاص که نشاندهنده خصوصیات مهمی از دادهها باشند.
منابع
[ویرایش]ویکی پدیای فارسی
درحال تحقیق...
پیشامدهای مستقل
استقلال یک مفهوم اساسی در نظریه احتمال است، مانند آمار و نظریه فرآیندهای تصادفی. دو رویداد مستقل، مستقل از نظر آماری، یا مستقل از تصادفی هستند. اگر، به طور غیررسمی، وقوع یکی بر احتمال وقوع دیگری تأثیری نداشته باشد یا به طور معادل، بر شانس تأثیری نداشته باشد. به طور مشابه، دو متغیر تصادفی مستقل هستند اگر تحقق یکی بر توزیع احتمال دیگری تأثیر نگذارد. هنگام برخورد با مجموعهای از بیش از دو رویداد، دو مفهوم استقلال باید از هم متمایز شوند. اگر هر دو رویداد در مجموعه مستقل از یکدیگر باشند، رویدادها به صورت زوجی مستقل نامیده می شوند، در حالی که استقلال متقابل (یا استقلال جمعی) رویدادها به معنای غیررسمی این است که هر رویداد مستقل از هر ترکیبی از رویدادهای دیگر در مجموعه است. مفهوم مشابهی برای مجموعه ای از متغیرهای تصادفی وجود دارد. استقلال متقابل مستلزم استقلال دوتایی است، اما نه برعکس. در ادبیات استاندارد تئوری احتمال، آمار و فرآیندهای تصادفی، استقلال بدون صلاحیت بیشتر معمولاً به استقلال متقابل اشاره دارد.[۱]
پیشامد مستقل اجتماع
[ویرایش]اگر دو پیشامد احتمالیAوBداشتم و باهم در نظریه مجموعه اجتماع هم دیگر شوند،به این صورت پیشامد نوشته می گردد:
در این پیشامد مستقل،دو احتمال جمع می گردد و پیشامد مسترک آنها در هم کم می گردد
مثال:
[ویرایش]اگر دو پیشامد AوB داشته باشیم و(P(Aو(P(B به ترتیب برابر با یک دوم و یک سوم باشد پیشامد اینگونه بدست می آید:
که برابر است با:
پیشامد مشترک
[ویرایش]اگر دو پیشامدAوB داشتم و باهم در مجموعه محاسبه اشتراک آنهارا بکنم،در هم ضرب می گردند:
منابع
[ویرایش]
فضای نمونه
در نظریه احتمال، فضای نمونه (که فضای توصیف نمونه یا فضای امکان نیز نامیده می شود) یک آزمایش یا آزمایش تصادفی مجموعه ای از تمام نتایج یا نتایج ممکن از آن آزمایش است. یک فضای نمونه معمولاً با استفاده از نماد مجموعه مشخص می شود و نتایج مرتب شده ممکن یا نقاط نمونه به عنوان عناصر در مجموعه فهرست می شوند. معمولاً به یک فضای نمونه با برچسب های S، Ω یا U (برای "مجموعه جهانی") اشاره می شود. عناصر یک فضای نمونه ممکن است اعداد، کلمات، حروف یا نمادها باشند. آنها همچنین می توانند متناهی، قابل شمارش نامتناهی یا غیرقابل شمارش نامتناهی باشند.
Aزیر مجموعه ای از فضای نمونه یک رویداد است که با نشان داده می شود. اگر نتیجه آزمایش در گنجانده شود، رویداد رخ داده است. برای مثال، اگر آزمایش یک سکه پرتاب میکند، فضای نمونه مجموعه است، جایی که نتیجه به این معنی است که سکه سر است. و نتیجه به این معنی است که سکه دم است. رویدادهای ممکن عبارتند از: ، و برای پرتاب دو سکه، فضای نمونه است که اگر هر دو سکه سر باشند نتیجه است، اگر سکه اول سر و دومی دم باشد، اگر سکه اول دم باشد و دومی سر باشد، و اگر هر دو سکه دم باشند . رویدادی که حداقل یکی از سکه ها سر باشد با داده می شود. برای پرتاب کردن یک قالب شش وجهی یکباره، جایی که نتیجه مورد نظر تعداد پیپ های رو به بالا است، فضای نمونه است. . یک فضای نمونه کاملاً تعریف شده و غیر خالی یکی از سه جزء در یک مدل احتمالی (یک فضای احتمالی) است. دو عنصر اساسی دیگر عبارتند از: یک مجموعه کاملاً تعریف شده از رویدادهای ممکن (یک فضای رویداد)، که معمولاً مجموعه توان است اگر گسسته یا یک & باشد. #x3C3;-جبر در اگر پیوسته باشد، و یک احتمال به هر رویداد اختصاص داده شده است (یک تابع اندازه گیری احتمال).

- قضیه:یک فضای نمونه را می توان به صورت بصری با یک مستطیل نشان داد، که نتایج فضای نمونه با نقاط درون مستطیل نشان داده می شود. رویدادها ممکن است با بیضی نشان داده شوند، جایی که نقاط محصور در بیضی، رویداد را تشکیل می دهند.
منابع
[ویرایش]https://en.m.wikipedia.org/wiki/Sample_space
جامعه و نمونه
جامعه و نمونه، دو عنصر کلی در آمار هستند که در آن نمونه جزئی از جامعه است،به این دو عنصر جامعه آماری و نمونه آماری می گویند.
تعریف
[ویرایش]جامعه آماری
[ویرایش]جامعه آماری عبارتست از مجموعه تمام افراد، گروهها، اشیاء و یا رویدادهایی که دارای یک یا چند ویژگی مشترک باشند. تعداد اعضای جامعه را حجم یا اندازه جامعه مینامند و با حرف بزرگ N نشان میدهند.
نمونه آماری
[ویرایش]نمونه آماری گروه کوچکتری از جامعه است که طبق ضابطهای معین برای مشاهده و تجزیه و تحلیل انتخاب میشود و باید معرف جامعه باشد. نتایج نمونه ای را که معرف جامعه نباشد نمیتوان به جامعه تعمیم داد. تعداد اعضای نمونه را با حرف کوچک n نشان می دهند.
نمونه گیری
[ویرایش]نمونهگیری به منظور گردآوری دادههای مورد نیاز درباره افراد جامعه و برآورد مقادیر جامعه به کمک مقادیر نمونه انجام میشود. نمونهگیری باعث صرفهجویی در هزینه و زمان است و کار تحقیق را ساده و امکانپذیر میسازد.
به طور کلی برای گردآوری اطلاعات دو روش وجود دارد:
الف) سرشماری: اگر محقق پژوهش خود را بر تمامی افراد جامعه اجرا کند روش او سرشماری خواهد بود. یعنی محقق باید تمامی افراد جامعه را تک تک مورد برسی و آزمون قرار دهد. هزینه، نیروی انسانی و مدت زمان لازم برای انجام شمارش کامل (برای گردآوری داده ها) به میزانی است که معمولاً اجرای آن توصیه نمی شود.
ب) نمونه گیری: نمونه گیری عبارت است از «انتخاب افراد گروه نمونه از میان اعضای یک جامعه ی تعریف شده ی آماری براساس اصول و قواعد خاص». در این شیوه دادهها از همه افراد جامعه گردآوری نمی شود.
منابع
[ویرایش]


































































































![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


![{\displaystyle \int _{a}^{b}\,f(x)dx=\left[F(x)\right]_{a}^{b}=F(b)-F(a)\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a433aea7c0c8b43e6387aa906e7d855c1cb1f207)
































![{\displaystyle {\displaystyle 0,2\pi [{\frac {x^{2}}{n}}sin(nx)-{\frac {2x}{n^{2}}}cos(nx)+{\frac {2}{n^{3}}}sin(nx)dx]=[0+{\frac {4\pi }{n}}-0-(0+0-0)]={\frac {4}{n}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a5bf327c3ae4f61cfc6824e92e1cd4aab552a94)

![{\displaystyle 0,2\pi [-{\frac {x^{2}}{n}}cos(nx)-{\frac {2x}{n^{2}}}sin(nx)+{\frac {2}{n^{3}}}cos(nx)dx]={\frac {1}{\pi }}[-{\frac {4\pi ^{2}}{n}}-0+{\frac {2}{n^{3}}}-0-0+{\frac {2}{n^{3}}}]=-{\frac {4\pi }{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f64537749da8b7bef4dfd10d6caf23c25eb85df3)
















![{\displaystyle f(t)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }[a_{n}\cos(\omega _{n}t)+b_{n}\sin(\omega _{n}t)]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/667370577e20c5f28121d05e55cf7197b6a2016e)
































![{\displaystyle {\begin{aligned}c_{n}&={\tfrac {1}{P}}\int _{P}\operatorname {Re} \{s(x)\}\cdot e^{-i{\frac {2\pi }{P}}nx}\ dx+i\cdot {\tfrac {1}{P}}\int _{P}\operatorname {Im} \{s(x)\}\cdot e^{-i{\tfrac {2\pi }{P}}nx}\ dx\\[4pt]&={\tfrac {1}{P}}\int _{P}\left(\operatorname {Re} \{s(x)\}+i\cdot \operatorname {Im} \{s(x)\}\right)\cdot e^{-i{\tfrac {2\pi }{P}}nx}\ dx\ =\ {\tfrac {1}{P}}\int _{P}s(x)\cdot e^{-i{\tfrac {2\pi }{P}}nx}\ dx.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2f3a7cab08bd95f922c1fbc2f921addb4edfcd3)
![{\displaystyle {\begin{aligned}s_{\infty }(x)&=\sum _{n=-\infty }^{\infty }{\hat {s}}[n]\cdot e^{i\,2\pi nx/P}\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}&&\scriptstyle {\mathsf {common\ engineering\ notation}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1a1ac253b5d7a763eff884963eb5efbc5dd0879)
![{\displaystyle S(f)\ \triangleq \ \sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6a4127cd2d8d239076aad35e6b82248554b6036)


![{\displaystyle {\begin{aligned}{\mathcal {F}}^{-1}\{S(f)\}&=\int _{-\infty }^{\infty }\left(\sum _{n=-\infty }^{\infty }S[n]\cdot \delta \left(f-{\frac {n}{P}}\right)\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot \int _{-\infty }^{\infty }\delta \left(f-{\frac {n}{P}}\right)e^{i2\pi fx}\,df,\\[6pt]&=\sum _{n=-\infty }^{\infty }S[n]\cdot e^{i\,2\pi nx/P}\ \ \triangleq \ s_{\infty }(x).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/446316db0d563e8ceac0da5d5d078b67f0c0f4e5)



































![{\displaystyle f(z)=\sum _{n=0}^{\infty }\left[a_{n}r^{n}\cos n\theta -b_{n}r^{n}\sin n\theta \right]+i\sum _{n=1}^{\infty }\left[a_{n}r^{n}\sin n\theta +b_{n}r^{n}\cos n\theta \right],\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9604da9974ced388ebfe69ec67f2fee98c901a73)


















![{\displaystyle \iiint _{V}\left[G\,\nabla \cdot \nabla u-u\,\nabla \cdot \nabla G\right]\,dV=\iiint _{V}\nabla \cdot \left[G\nabla u-u\nabla G\right]\,dV=\iint _{S}\left[Gu_{n}-uG_{n}\right]\,dS.\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5b42331f8ae6edb5abb438f575369019cba8f4d3)











































































































































































































































































![{\displaystyle A={\frac {n}{4}}\left[\left(a_{1}^{2}+a_{2}^{2}\right)\cot {\frac {\pi }{n}}+{\sqrt {\left(a_{1}^{2}-a_{2}^{2}\right)^{2}\sec ^{2}{\frac {\pi }{n}}+4h^{2}\left(a_{1}+a_{2}\right)^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57c9ba44195955a9024eca9605b00b44cdbe785a)






























































![{\displaystyle \in [0,h]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/720699950e274dea9ac9ef66c70149f86d5786bc)


























![{\displaystyle \!V=\pi \left[r^{2}h-{\frac {h^{3}}{3}}\right]_{0}^{r}=\pi \left(r^{3}-{\frac {r^{3}}{3}}\right)-\pi \left(-0^{3}+{\frac {0^{3}}{3}}\right)={\frac {2}{3}}\pi r^{3}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ed326b489748f931992277f48fce44ae5e4c7623)

















![{\displaystyle V=\pi r^{2}\left[x\right]_{-r}^{r}-{\frac {1}{3}}\pi \left[{x^{3}}\right]_{-r}^{r}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6a0bdfef74621c05105237e5ad5307e46541426)
![{\displaystyle V=\pi r^{2}\left[r-(-r)\right]-{\frac {1}{3}}\pi \left[r^{3}-(-r)^{3}\right]=2\pi r^{3}-{\frac {2}{3}}\pi r^{3}={\frac {4}{3}}\pi r^{3}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8e8b644c410efef3c860f803151b559f0e5b561)

![{\displaystyle V_{\mathrm {KS} }=\int _{r-h}^{r}{A_{x}\,\mathrm {d} x}=\pi r^{2}\left[x\right]_{r-h}^{r}-{\frac {1}{3}}\pi \left[{x^{3}}\right]_{r-h}^{r}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e3eac1232a18271d5315396f1a3962d66b8b799)
![{\displaystyle V_{\mathrm {KS} }=\pi r^{2}\left[r-(r-h)\right]-{\frac {1}{3}}\pi \left[r^{3}-(r-h)^{3}\right]=\pi r^{2}h-{\frac {1}{3}}\pi \left[r^{3}-(r^{3}-3r^{2}h+3rh^{2}-h^{3})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2542735740c1db5826e1eb8a38e772457d4602ca)














![{\displaystyle {\begin{aligned}\int _{K}\!\mathrm {d} V&=\int \limits _{0}^{2\pi }\int \limits _{0}^{R}2{\sqrt {R^{2}-r^{2}}}\;r\,\mathrm {d} r\,\mathrm {d} \varphi \\&=2\pi \int \limits _{0}^{R}2{\sqrt {R^{2}-r^{2}}}\;r\,\mathrm {d} r\\&=2\pi (-1){\frac {2}{3}}\left[{\sqrt {(R^{2}-r^{2})^{3}}}\right]_{r=0}^{R}\\&={\frac {4}{3}}\pi R^{3}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c23fd89b7df891c3613bd42210631ffcea85c2f)
![{\displaystyle V=\pi \int _{a}^{b}[f(x)]^{2}\mathrm {d} x=\pi \int _{a}^{b}y^{2}\,\mathrm {d} x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b7c6c7a545aea40bde71da9577c4d2460ad61d66)



![{\displaystyle {\begin{aligned}V_{\text{Kugel}}&=\pi \int _{-r}^{r}\left(r^{2}-x^{2}\right)\,\mathrm {d} x\\&=\pi \left[r^{2}x-{\frac {1}{3}}x^{3}\right]_{-r}^{r}\\&=\pi \left(r^{3}-{\frac {1}{3}}r^{3}\right)-\pi \left(r^{2}\cdot (-r)-{\frac {1}{3}}(-r)^{3}\right)\\&=\pi \left[\left({\frac {2}{3}}r^{3}\right)-\left(-{\frac {2}{3}}r^{3}\right)\right]\\&={\frac {4}{3}}\pi r^{3}.\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b849b51779abd5f1ca4d58f5835dca5cade18f6)























































































![{\displaystyle k[x_{1},...,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c94122b5f7993f4d088b504b7118b4d914b35d1)




![{\displaystyle k[\mathbb {A} ^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5a59ad2c4843393bb4e679b7982dc8388adb233)













![{\displaystyle K[V]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec5fddcd6d55d1d9c792a53117274e8637be0e33)
![{\displaystyle K[\mathbb {A} ^{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4eddfb520d34a5fc2ea02f3745d0d9095b357d3f)


![{\displaystyle K[\mathbb {A} ^{n}]/I(V)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/077cdda9824e05053091314f21558055f7d1dab5)



![{\displaystyle n[(n'-2){\frac {180}{n'}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5432b8fd405ab1c5587cf37c266848ece9280e60)





















































































































































![{\displaystyle 180n[(n'-2)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26fea94fdda622ad336c2cc2bd229aff27ce8b79)
![{\displaystyle {\frac {180}{n'}}n[(n'-2)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63aa0333885a073baac3ca226abffc21da16f525)

![{\displaystyle n[{\frac {1}{4}}n'a^{2}cot({\frac {\pi }{n'}})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/906905024416501a0aad6d37e924f89394d995bf)
























































































































































![{\displaystyle {\begin{aligned}\int _{0}^{2\pi }\int _{0}^{\theta }\sin \theta '\,d\theta '\,d\phi &=\int _{0}^{2\pi }d\phi \int _{0}^{\theta }\sin \theta '\,d\theta '\\&=2\pi \int _{0}^{\theta }\sin \theta '\,d\theta '\\&=2\pi \left[-\cos \theta '\right]_{0}^{\theta }\\&=2\pi \left(1-\cos \theta \right).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/553bfb7326b3102cfc2e03f81cf7b34da431296b)


![{\displaystyle \Omega =2\left[\arccos \left({\frac {\sin \gamma }{\sin \theta }}\right)-\cos \theta \arccos \left({\frac {\tan \gamma }{\tan \theta }}\right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6801ed323a0f13ac7a1460c6549fa0b15002269d)
















































![{\displaystyle \Pr(A)=E[\Pr(A\mid N)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74f2ad6d5d0fb85d1d5f6adae1433618c3f5f335)

















![{\displaystyle (4\times 36\times 45\times 50\times 75)^{\frac {1}{5}}={\sqrt[{5}]{24\;300\;000}}=30}](https://wikimedia.org/api/rest_v1/media/math/render/svg/183fe59601b54283b5cf76236042adc0314723ca)









































